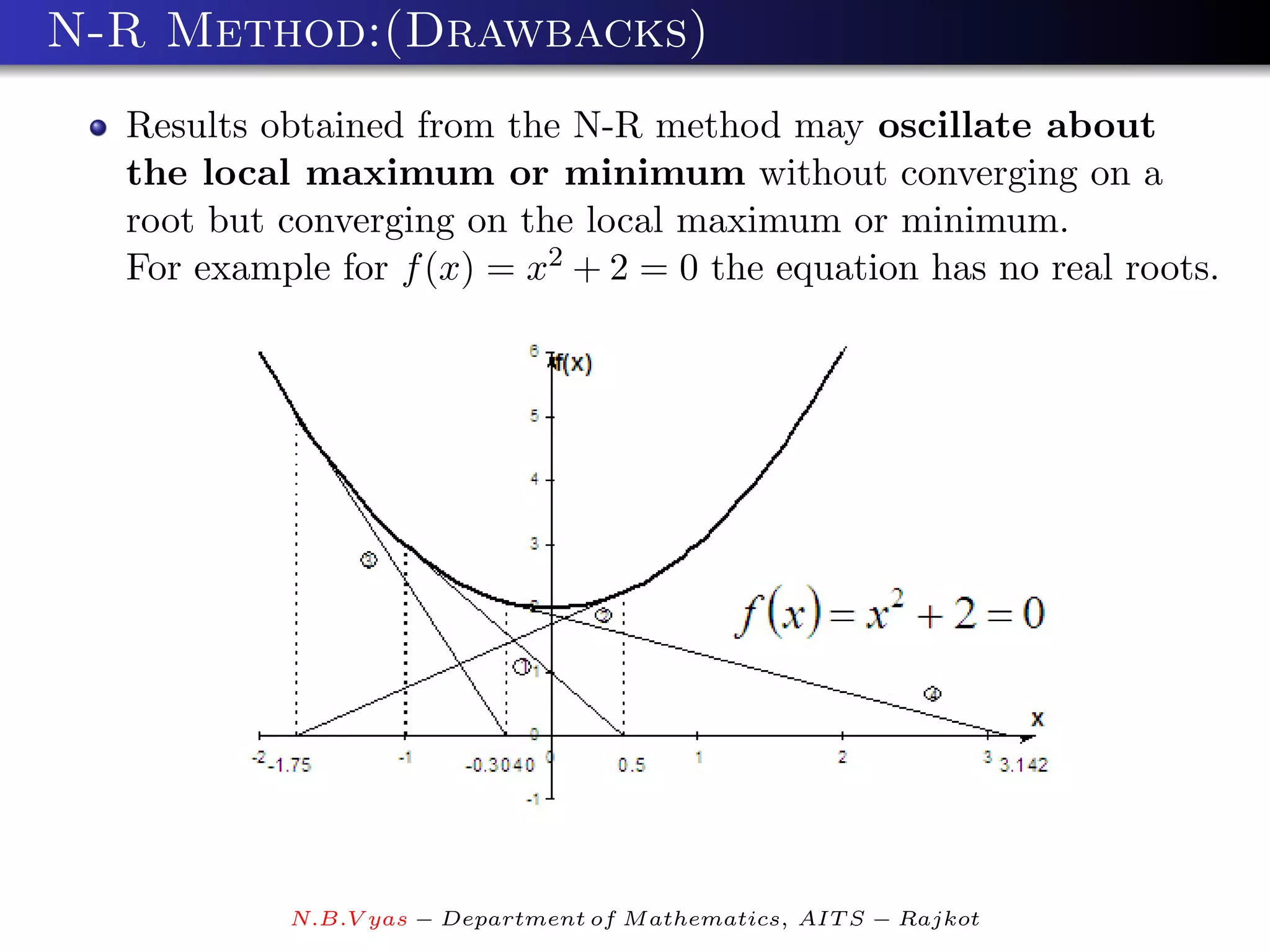
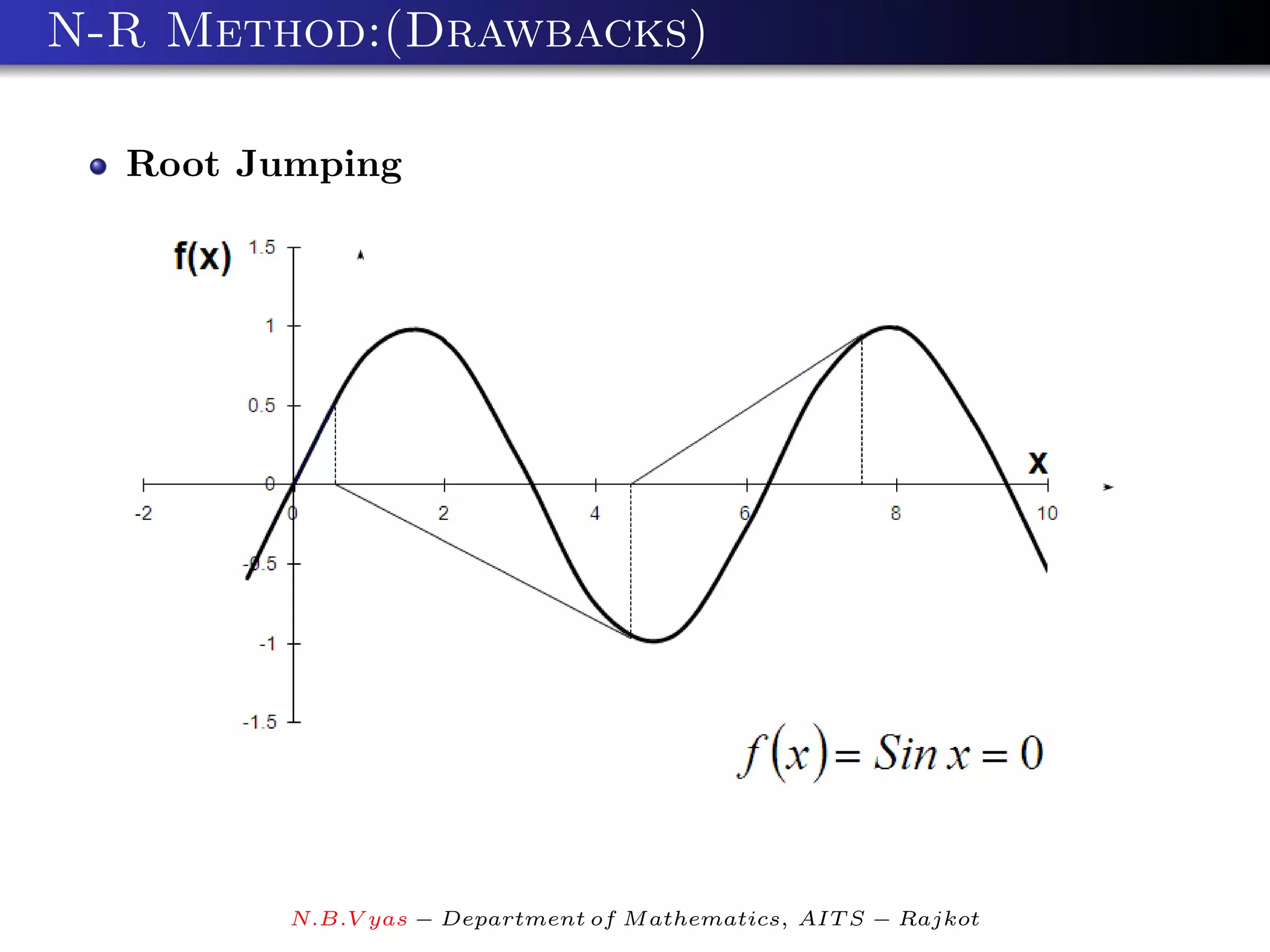
The document discusses numerical methods for finding roots of functions. It introduces the bisection method for finding a root of a continuous function f(x) within a given interval [a,b] where f(a) and f(b) have opposite signs. The method bisects the interval into two subintervals and recursively narrows in on the root by testing the sign of f(x) at the midpoint of each subinterval. An example applies the bisection method to find a root of the function f(x)=x^3-x-1 between 1 and 2.

1. Numerical Methods
N. B. Vyas
Department of Mathematics,
Atmiya Institute of Tech. and Science,
Rajkot (Guj.)
N.B.V yas − Department of M athematics, AIT S − Rajkot

2. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
N.B.V yas − Department of M athematics, AIT S − Rajkot

3. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
An algebraic function is informally a function that
satisfies a polynomial equation
N.B.V yas − Department of M athematics, AIT S − Rajkot

4. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
An algebraic function is informally a function that
satisfies a polynomial equation
A function which is not algebraic is called a transcendental
function.
N.B.V yas − Department of M athematics, AIT S − Rajkot

5. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
An algebraic function is informally a function that
satisfies a polynomial equation
A function which is not algebraic is called a transcendental
function.
The values of x which satisfy the equation f (x) = 0 are
called roots of f (x).
N.B.V yas − Department of M athematics, AIT S − Rajkot

6. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
An algebraic function is informally a function that
satisfies a polynomial equation
A function which is not algebraic is called a transcendental
function.
The values of x which satisfy the equation f (x) = 0 are
called roots of f (x).
If f (x) is quadratic, cubic or bi-quadratic expression, then
algebraic formulae are available for getting the solution.
N.B.V yas − Department of M athematics, AIT S − Rajkot

7. Introduction
There are two types of functions: (i) Algebraic function and
(ii) Transcendental function
An algebraic function is informally a function that
satisfies a polynomial equation
A function which is not algebraic is called a transcendental
function.
The values of x which satisfy the equation f (x) = 0 are
called roots of f (x).
If f (x) is quadratic, cubic or bi-quadratic expression, then
algebraic formulae are available for getting the solution.
If f (x) is a higher degree polynomial or transcendental
function then algebraic methods are not available.
N.B.V yas − Department of M athematics, AIT S − Rajkot

8. Errors
It is never possible to measure anything exactly.
N.B.V yas − Department of M athematics, AIT S − Rajkot

9. Errors
It is never possible to measure anything exactly.
So in order to make valid conclusions, it is good to make the
error as small as possible.
N.B.V yas − Department of M athematics, AIT S − Rajkot

10. Errors
It is never possible to measure anything exactly.
So in order to make valid conclusions, it is good to make the
error as small as possible.
The result of any physical measurement has two essential
components :
N.B.V yas − Department of M athematics, AIT S − Rajkot

11. Errors
It is never possible to measure anything exactly.
So in order to make valid conclusions, it is good to make the
error as small as possible.
The result of any physical measurement has two essential
components :
i) A numerical value
N.B.V yas − Department of M athematics, AIT S − Rajkot

12. Errors
It is never possible to measure anything exactly.
So in order to make valid conclusions, it is good to make the
error as small as possible.
The result of any physical measurement has two essential
components :
i) A numerical value
ii) A degree of uncertainty Or Errors.
N.B.V yas − Department of M athematics, AIT S − Rajkot

13. Errors
Exact Numbers: There are the numbers in which there is
no uncertainty and no approximation.
N.B.V yas − Department of M athematics, AIT S − Rajkot

14. Errors
Exact Numbers: There are the numbers in which there is
no uncertainty and no approximation.
Approximate Numbers: These are the numbers which
represent a certain degree of accuracy but not the exact
value.
N.B.V yas − Department of M athematics, AIT S − Rajkot

15. Errors
Exact Numbers: There are the numbers in which there is
no uncertainty and no approximation.
Approximate Numbers: These are the numbers which
represent a certain degree of accuracy but not the exact
value.
These numbers cannot be represented in terms of finite
number of digits.
N.B.V yas − Department of M athematics, AIT S − Rajkot

16. Errors
Exact Numbers: There are the numbers in which there is
no uncertainty and no approximation.
Approximate Numbers: These are the numbers which
represent a certain degree of accuracy but not the exact
value.
These numbers cannot be represented in terms of finite
number of digits.
Significant Digits: It refers to the number of digits in a
number excluding leading zeros.
N.B.V yas − Department of M athematics, AIT S − Rajkot

17. Bisection Method
Consider a continuous function f (x).
N.B.V yas − Department of M athematics, AIT S − Rajkot

18. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
N.B.V yas − Department of M athematics, AIT S − Rajkot

19. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
N.B.V yas − Department of M athematics, AIT S − Rajkot

20. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
N.B.V yas − Department of M athematics, AIT S − Rajkot

21. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
Now according to Bisection method, bisect the interval [a, b],
a+b
x1 = (a < x1 < b).
2
N.B.V yas − Department of M athematics, AIT S − Rajkot

22. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
Now according to Bisection method, bisect the interval [a, b],
a+b
x1 = (a < x1 < b).
2
If f (x1 ) = 0 then x1 be the root of the given equation.
N.B.V yas − Department of M athematics, AIT S − Rajkot

23. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
Now according to Bisection method, bisect the interval [a, b],
a+b
x1 = (a < x1 < b).
2
If f (x1 ) = 0 then x1 be the root of the given equation.
Otherwise the root lies between x1 and b if f (x1 ) < 0.
N.B.V yas − Department of M athematics, AIT S − Rajkot

24. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
Now according to Bisection method, bisect the interval [a, b],
a+b
x1 = (a < x1 < b).
2
If f (x1 ) = 0 then x1 be the root of the given equation.
Otherwise the root lies between x1 and b if f (x1 ) < 0.
OR the root lies between a and x1 if f (x1 ) > 0.
Then again bisect this interval to get next point x2 .
N.B.V yas − Department of M athematics, AIT S − Rajkot

25. Bisection Method
Consider a continuous function f (x).
Numbers a < b such that f (a) and f (b) have opposite signs.
Let f (a) be negative and f (b) be positive for [a, b].
Then there exists at least one point(root), say x, a < x < b
such that f (x) = 0.
Now according to Bisection method, bisect the interval [a, b],
a+b
x1 = (a < x1 < b).
2
If f (x1 ) = 0 then x1 be the root of the given equation.
Otherwise the root lies between x1 and b if f (x1 ) < 0.
OR the root lies between a and x1 if f (x1 ) > 0.
Then again bisect this interval to get next point x2 .
Repeat the above procedure to generate x1 , x2 , . . . till the
root upto desired accuracy is obtained.
N.B.V yas − Department of M athematics, AIT S − Rajkot

26. Bisection Method
Characteristics:
1 This method always slowly converge to a root.
N.B.V yas − Department of M athematics, AIT S − Rajkot

27. Bisection Method
Characteristics:
1 This method always slowly converge to a root.
2 It gives only one root at a time on the the selection of small
interval near the root.
N.B.V yas − Department of M athematics, AIT S − Rajkot

28. Bisection Method
Characteristics:
1 This method always slowly converge to a root.
2 It gives only one root at a time on the the selection of small
interval near the root.
3 In case of the multiple roots of an equation, other initial
interval can be chosen.
N.B.V yas − Department of M athematics, AIT S − Rajkot

29. Bisection Method
Characteristics:
1 This method always slowly converge to a root.
2 It gives only one root at a time on the the selection of small
interval near the root.
3 In case of the multiple roots of an equation, other initial
interval can be chosen.
4 Smallest interval must be selected to obtain immediate
convergence to the root, .
N.B.V yas − Department of M athematics, AIT S − Rajkot

30. Bisection Method- Example
Ex. Find real root of x3 − x − 1 = 0 correct upto three
decimal places using Bisection method
N.B.V yas − Department of M athematics, AIT S − Rajkot

31. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
N.B.V yas − Department of M athematics, AIT S − Rajkot

32. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) =
N.B.V yas − Department of M athematics, AIT S − Rajkot

33. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
N.B.V yas − Department of M athematics, AIT S − Rajkot

34. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) =
N.B.V yas − Department of M athematics, AIT S − Rajkot

35. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
N.B.V yas − Department of M athematics, AIT S − Rajkot

36. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) =
N.B.V yas − Department of M athematics, AIT S − Rajkot

37. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) = 5 > 0
N.B.V yas − Department of M athematics, AIT S − Rajkot

38. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) = 5 > 0
∴ since f (x) is continuous function there must be a root in the
lying in the interval (1, 2)
N.B.V yas − Department of M athematics, AIT S − Rajkot

39. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) = 5 > 0
∴ since f (x) is continuous function there must be a root in the
lying in the interval (1, 2)
Now according to Bisection method, the next approximation
is obtained by taking the midpoint of (1, 2)
N.B.V yas − Department of M athematics, AIT S − Rajkot

40. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) = 5 > 0
∴ since f (x) is continuous function there must be a root in the
lying in the interval (1, 2)
Now according to Bisection method, the next approximation
is obtained by taking the midpoint of (1, 2)
1+2
c= = 1.5, f (1.5) =
2
N.B.V yas − Department of M athematics, AIT S − Rajkot

41. Bisection Method- Example
Sol. Let f (x) = x3 − x − 1 = 0
f (0) = −1 < 0
f (1) = −1 < 0
f (2) = 5 > 0
∴ since f (x) is continuous function there must be a root in the
lying in the interval (1, 2)
Now according to Bisection method, the next approximation
is obtained by taking the midpoint of (1, 2)
1+2
c= = 1.5, f (1.5) =
2
a+b
No. of a b c= f(c)
2
iterations (f (a) < 0) (f (b) > 0) (< 0, > 0)
1 1 2 1.5 -
N.B.V yas − Department of M athematics, AIT S − Rajkot

42. Bisection Method- Example
Ex. Find real root of x3 − 4x + 1 = 0 correct upto four
decimal places using Bisection method
N.B.V yas − Department of M athematics, AIT S − Rajkot

43. Bisection Method- Example
Ex. Find real root of x2 − lnx − 12 = 0 correct upto
three decimal places using Bisection method
N.B.V yas − Department of M athematics, AIT S − Rajkot

44. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
N.B.V yas − Department of M athematics, AIT S − Rajkot

45. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
N.B.V yas − Department of M athematics, AIT S − Rajkot

46. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 .
N.B.V yas − Department of M athematics, AIT S − Rajkot

47. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
N.B.V yas − Department of M athematics, AIT S − Rajkot

48. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
AB
Now ∠ACB = α, tanα =
AC
N.B.V yas − Department of M athematics, AIT S − Rajkot

49. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
AB
Now ∠ACB = α, tanα =
AC
f (x0 )
∴ f (x0 ) =
x0 − x1
N.B.V yas − Department of M athematics, AIT S − Rajkot

50. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
AB
Now ∠ACB = α, tanα =
AC
f (x0 )
∴ f (x0 ) =
x0 − x1
f (x0 f (x0
∴ x0 − x1 = ⇒ x0 − = x1
f (x0 ) f (x0 )
N.B.V yas − Department of M athematics, AIT S − Rajkot

51. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
AB
Now ∠ACB = α, tanα =
AC
f (x0 )
∴ f (x0 ) =
x0 − x1
f (x0 f (x0
∴ x0 − x1 = ⇒ x0 − = x1
f (x0 ) f (x0 )
f (x0 )
∴ x1 = x0 −
f (x0 )
N.B.V yas − Department of M athematics, AIT S − Rajkot

52. Newton-Raphson Method(N-R Method)
Graphical derivation of the Method:
Consider the portion of the graph y = f (x) which crosses
X − axis at R corresponding to the equation f (x) = 0.
Let B be the point on the curve corresponding to the initial
guess x0 at A.
The tangent at B cuts the X − axis at C which gives first
approximation x1 . Thus AB = f (x0 ) and AC = x0 − x1
AB
Now ∠ACB = α, tanα =
AC
f (x0 )
∴ f (x0 ) =
x0 − x1
f (x0 f (x0
∴ x0 − x1 = ⇒ x0 − = x1
f (x0 ) f (x0 )
f (x0 )
∴ x1 = x0 −
f (x0 )
f (xn )
In general xn+1 = xn − ; where n = 0, 1, 2, 3, . . .
f (xn )
N.B.V yas − Department of M athematics, AIT S − Rajkot

53. Derivation of the Newton-
Raphson method.
f(x)
y= f(x)
AB
tan(α ) =
f(x0 ) B AC
f ( x0 )
f '( x 0) =
x0 − x1
f ( x0 )
R C α A x1 = x0 −
X f ′( x0 )
x1 x0
4
N.B.V yas − Department of M athematics, AIT S − Rajkot

54. Newton-Raphson method
f(x)
f(x0 ) f(xn )
 x0, f ( x0 ) xn +1 = xn -
  f ′ (xn )
f(x 1)
α
x2 x1 x0 X
3
N.B.V yas − Department of M athematics, AIT S − Rajkot

55. N-R Method:
Advantages:
Converges Fast (if it converges).
Requires only one guess.
N.B.V yas − Department of M athematics, AIT S − Rajkot

56. Drawbacks:
Divergence at inflection point.
Selection of the initial guess or an iteration value of the root that
is close to the inflection point of the function f (x) may start
diverging away from the root in the Newton-Raphson method.
N.B.V yas − Department of M athematics, AIT S − Rajkot

57. N-R Method:(Drawbacks)
Division by zero
N.B.V yas − Department of M athematics, AIT S − Rajkot

58. N-R Method:(Drawbacks)
Results obtained from the N-R method may oscillate about
the local maximum or minimum without converging on a
root but converging on the local maximum or minimum.
For example for f (x) = x2 + 2 = 0 the equation has no real roots.
N.B.V yas − Department of M athematics, AIT S − Rajkot

59. N-R Method:(Drawbacks)
Root Jumping
N.B.V yas − Department of M athematics, AIT S − Rajkot

60. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
N.B.V yas − Department of M athematics, AIT S − Rajkot

61. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
N.B.V yas − Department of M athematics, AIT S − Rajkot

62. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
∴ f (x) = qxq−1
N.B.V yas − Department of M athematics, AIT S − Rajkot

63. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
∴ f (x) = qxq−1
f (xn ) (xn )q − N
Now by N-R method, xn+1 = xn − = xn −
f (xn ) q(xn )q−1
N.B.V yas − Department of M athematics, AIT S − Rajkot

64. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
∴ f (x) = qxq−1
f (xn ) (xn )q − N
Now by N-R method, xn+1 = xn − = xn −
f (xn ) q(xn )q−1
1 N
= xn − xn +
q q(xn )q−1
N.B.V yas − Department of M athematics, AIT S − Rajkot

65. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
∴ f (x) = qxq−1
f (xn ) (xn )q − N
Now by N-R method, xn+1 = xn − = xn −
f (xn ) q(xn )q−1
1 N
= xn − xn +
q q(xn )q−1
1 N
xn+1 = (q − 1)xn + ; n = 0, 1, 2, . . .
q (xn )q−1
N.B.V yas − Department of M athematics, AIT S − Rajkot

66. N-R Method
Iterative formula for finding q th root:
1
xq − N = 0 i.e. x = N q
Let f (x) = xq − N
∴ f (x) = qxq−1
f (xn ) (xn )q − N
Now by N-R method, xn+1 = xn − = xn −
f (xn ) q(xn )q−1
1 N
= xn − xn +
q q(xn )q−1
1 N
xn+1 = (q − 1)xn + ; n = 0, 1, 2, . . .
q (xn )q−1
N.B.V yas − Department of M athematics, AIT S − Rajkot

67. N-R Method
Iterative formula for finding reciprocal of a positive number
N:
1 1
x= i.e. − N = 0
N x
1
Let f (x) = − N
x
N.B.V yas − Department of M athematics, AIT S − Rajkot

68. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
N.B.V yas − Department of M athematics, AIT S − Rajkot

69. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
N.B.V yas − Department of M athematics, AIT S − Rajkot

70. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
Often it requires a very good initial guess.
N.B.V yas − Department of M athematics, AIT S − Rajkot

71. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
Often it requires a very good initial guess.
To overcome these drawbacks, the derivative of f of the function
f (xn−1 ) − f (xn )
f is approximated as f (xn ) =
xn−1 − xn
N.B.V yas − Department of M athematics, AIT S − Rajkot

72. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
Often it requires a very good initial guess.
To overcome these drawbacks, the derivative of f of the function
f (xn−1 ) − f (xn )
f is approximated as f (xn ) =
xn−1 − xn
Therefore formula of N-R method becomes
N.B.V yas − Department of M athematics, AIT S − Rajkot

73. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
Often it requires a very good initial guess.
To overcome these drawbacks, the derivative of f of the function
f (xn−1 ) − f (xn )
f is approximated as f (xn ) =
xn−1 − xn
Therefore formula of N-R method becomes
f (xn )
xn+1 = xn −
f (xn−1 )−f (xn )
xn−1 −xn
N.B.V yas − Department of M athematics, AIT S − Rajkot

74. Secant Method
In N-R method two functions f and f are required to be
evaluate per step.
Also it requires to evaluate derivative of f and sometimes it is
very complicated to evaluate f .
Often it requires a very good initial guess.
To overcome these drawbacks, the derivative of f of the function
f (xn−1 ) − f (xn )
f is approximated as f (xn ) =
xn−1 − xn
Therefore formula of N-R method becomes
f (xn )
xn+1 = xn −
f (xn−1 )−f (xn )
xn−1 −xn
xn−1 − xn
∴ xn+1 = xn − f (xn )
f (xn−1 ) − f (xn )
where n = 1, 2, 3, . . ., f (xn−1 ) = f (xn )
N.B.V yas − Department of M athematics, AIT S − Rajkot

75. Secant Method
This method requires two initial guesses
N.B.V yas − Department of M athematics, AIT S − Rajkot

76. Secant Method
This method requires two initial guesses
The two initial guesses do not need to bracket the root of the
equation, so it is not classified as a bracketing method.
N.B.V yas − Department of M athematics, AIT S − Rajkot

77. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
N.B.V yas − Department of M athematics, AIT S − Rajkot

78. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
Draw the straight line through the points (xn , f (xn )) and
(xn−1 , f (xn−1 ))
N.B.V yas − Department of M athematics, AIT S − Rajkot

79. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
Draw the straight line through the points (xn , f (xn )) and
(xn−1 , f (xn−1 ))
Take the x−coordinate of intersection with X−axis as xn+1
N.B.V yas − Department of M athematics, AIT S − Rajkot

80. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
Draw the straight line through the points (xn , f (xn )) and
(xn−1 , f (xn−1 ))
Take the x−coordinate of intersection with X−axis as xn+1
From the figure ABE and DCE are similar triangles.
N.B.V yas − Department of M athematics, AIT S − Rajkot

81. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
Draw the straight line through the points (xn , f (xn )) and
(xn−1 , f (xn−1 ))
Take the x−coordinate of intersection with X−axis as xn+1
From the figure ABE and DCE are similar triangles.
AB AE f (xn ) xn − xn+1
Hence = ⇒ =
DC DE f (xn−1 ) xn−1 − xn+1
N.B.V yas − Department of M athematics, AIT S − Rajkot

82. Secant Method
Geometrical interpretation of Secant Method:
Consider a continuous function y = f (x)
Draw the straight line through the points (xn , f (xn )) and
(xn−1 , f (xn−1 ))
Take the x−coordinate of intersection with X−axis as xn+1
From the figure ABE and DCE are similar triangles.
AB AE f (xn ) xn − xn+1
Hence = ⇒ =
DC DE f (xn−1 ) xn−1 − xn+1
xn−1 − xn
∴ xn+1 = xn − f (xn )
f (xn−1 ) − f (xn )
N.B.V yas − Department of M athematics, AIT S − Rajkot

83. Secant Method
NOTE:
Do not combine the secant formula and write it in the form as
follows because it has enormous loss of significance errors
xn f (xn−1 ) − xn−1 f (xn )
xn+1 =
f (xn−1 ) − f (xn )
N.B.V yas − Department of M athematics, AIT S − Rajkot

84. Secant Method
General Features:
The secant method is an open method and may not converge.
N.B.V yas − Department of M athematics, AIT S − Rajkot

85. Secant Method
General Features:
The secant method is an open method and may not converge.
It requires fewer function evaluations.
N.B.V yas − Department of M athematics, AIT S − Rajkot

86. Secant Method
General Features:
The secant method is an open method and may not converge.
It requires fewer function evaluations.
In some problems the secant method will work when Newton’s
method does not and vice-versa.
N.B.V yas − Department of M athematics, AIT S − Rajkot

87. Secant Method
General Features:
The secant method is an open method and may not converge.
It requires fewer function evaluations.
In some problems the secant method will work when Newton’s
method does not and vice-versa.
The method is usually a bit slower than Newton’s method. It is
more rapidly convergent than the bisection method.
N.B.V yas − Department of M athematics, AIT S − Rajkot

88. Secant Method
General Features:
The secant method is an open method and may not converge.
It requires fewer function evaluations.
In some problems the secant method will work when Newton’s
method does not and vice-versa.
The method is usually a bit slower than Newton’s method. It is
more rapidly convergent than the bisection method.
This method does not require use of the derivative of the
function.
N.B.V yas − Department of M athematics, AIT S − Rajkot

89. Secant Method
General Features:
The secant method is an open method and may not converge.
It requires fewer function evaluations.
In some problems the secant method will work when Newton’s
method does not and vice-versa.
The method is usually a bit slower than Newton’s method. It is
more rapidly convergent than the bisection method.
This method does not require use of the derivative of the
function.
This method requires only one function evaluation per iteration.
N.B.V yas − Department of M athematics, AIT S − Rajkot

90. Secant Method
Disadvantages:
There is no guaranteed error bound for the computed value.
N.B.V yas − Department of M athematics, AIT S − Rajkot

91. Secant Method
Disadvantages:
There is no guaranteed error bound for the computed value.
It is likely to difficulty of f (x) = 0. This means X−axis is
tangent to the graph of y = f (x)
N.B.V yas − Department of M athematics, AIT S − Rajkot

92. Secant Method
Disadvantages:
There is no guaranteed error bound for the computed value.
It is likely to difficulty of f (x) = 0. This means X−axis is
tangent to the graph of y = f (x)
Method may converge very slowly or not at all.
N.B.V yas − Department of M athematics, AIT S − Rajkot