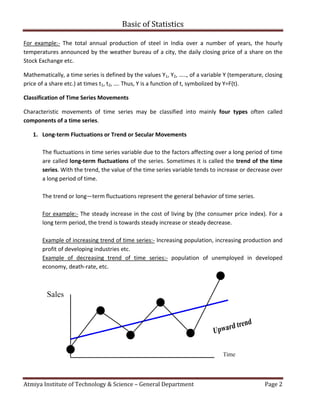
The document discusses forecasting methods in numerical and statistical methods for computer engineering, emphasizing the importance of predicting future conditions for decision-making in uncertain environments. It defines time series and categorizes its components into trend, cyclical, seasonal, and irregular fluctuations, with explanations of various forecasting methods including freehand, semi-averages, and moving averages. These methods aim to assist in estimating future values based on historical data trends.