Let Pn(x) be the Legendre polynomial of degree n. Then the generating function for Pn(x) is given by: ∞ 1 Pn(x)tn = √ n=0 1 − 2xt + t2 Differentiating both sides with respect to t, we get: ∞ ∑nPn(x)tn-1 = -xt(1 − 2xt + t2)-1/2 + (1 − 2xt + t2)-3/2 n=1 Multiplying both sides by (1 − 2xt + t2)1/2, we get: ∞ ∑

1. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Function
N. B. Vyas
Department of Mathematics
Atmiya Institute of Technology and Science
Department of Mathematics
N. B. Vyas Legendre’s Function

2. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
The differential equation
N. B. Vyas Legendre’s Function

3. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
The differential equation
2
(1 − x )y − 2xy + n(n + 1)y = 0
N. B. Vyas Legendre’s Function

4. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
The differential equation
2
(1 − x )y − 2xy + n(n + 1)y = 0
is called Legendre’s differential equation,
n is real constant
N. B. Vyas Legendre’s Function

5. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
N. B. Vyas Legendre’s Function

6. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
⇒ P1 (x) = x
N. B. Vyas Legendre’s Function

7. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
⇒ P1 (x) = x
1
⇒ P2 (x) = (3x2 − 1)
2
N. B. Vyas Legendre’s Function

8. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
⇒ P1 (x) = x
1
⇒ P2 (x) = (3x2 − 1)
2
1
⇒ P3 (x) = (5x3 − 3x)
2
N. B. Vyas Legendre’s Function

9. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
⇒ P1 (x) = x
1
⇒ P2 (x) = (3x2 − 1)
2
1
⇒ P3 (x) = (5x3 − 3x)
2
1
⇒ P4 (x) = (35x3 − 30x2 + 3)
8
N. B. Vyas Legendre’s Function

10. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Legendre’s Polynomials:
⇒ P0 (x) = 1
⇒ P1 (x) = x
1
⇒ P2 (x) = (3x2 − 1)
2
1
⇒ P3 (x) = (5x3 − 3x)
2
1
⇒ P4 (x) = (35x3 − 30x2 + 3)
8
1
⇒ P5 (x) = (63x5 − 70x3 + 15x)
8
N. B. Vyas Legendre’s Function

11. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex.1 Express f (x) in terms of
Legendre’s polynomials where
f (x) = x3 + 2x2 − x − 3.
N. B. Vyas Legendre’s Function

12. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
N. B. Vyas Legendre’s Function

13. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
N. B. Vyas Legendre’s Function

14. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
N. B. Vyas Legendre’s Function

15. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
1
⇒ P3 (x) = (5x3 − 3x)
2
N. B. Vyas Legendre’s Function

16. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
1
⇒ P3 (x) = (5x3 − 3x)
2
∴ 2P3 (x) = (5x3 − 3x)
N. B. Vyas Legendre’s Function

17. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
1
⇒ P3 (x) = (5x3 − 3x)
2
∴ 2P3 (x) = (5x3 − 3x)
∴ 2P3 (x) + 3x = 5x3
N. B. Vyas Legendre’s Function

18. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
1
⇒ P3 (x) = (5x3 − 3x)
2
∴ 2P3 (x) = (5x3 − 3x)
∴ 2P3 (x) + 3x = 5x3
∴ 2P3 (x) + 3P1 (x) = 5x3 { x = P1 (x)}
N. B. Vyas Legendre’s Function

19. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
⇒ P0 (x) = 1
∴ 1 = P0 (x)
⇒ P1 (x) = x
∴ x = P1 (x)
1
⇒ P3 (x) = (5x3 − 3x)
2
∴ 2P3 (x) = (5x3 − 3x)
∴ 2P3 (x) + 3x = 5x3
∴ 2P3 (x) + 3P1 (x) = 5x3 { x = P1 (x)}
2 3
∴ x3 = P3 (x) + P1 (x)
5 5
N. B. Vyas Legendre’s Function

20. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
N. B. Vyas Legendre’s Function

21. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
N. B. Vyas Legendre’s Function

22. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
∴ 2P2 (x) + 1 = 3x2
N. B. Vyas Legendre’s Function

23. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
∴ 2P2 (x) + 1 = 3x2
∴ 2P2 (x) + P0 (x) = 3x2 { 1 = P0 (x)}
N. B. Vyas Legendre’s Function

24. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
∴ 2P2 (x) + 1 = 3x2
∴ 2P2 (x) + P0 (x) = 3x2 { 1 = P0 (x)}
2 1
∴ x2 = P2 (x) + P0 (x)
3 3
N. B. Vyas Legendre’s Function

25. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
∴ 2P2 (x) + 1 = 3x2
∴ 2P2 (x) + P0 (x) = 3x2 { 1 = P0 (x)}
2 1
∴ x2 = P2 (x) + P0 (x)
3 3
Now, f (x) = x3 + 2x2 − x − 3
N. B. Vyas Legendre’s Function

26. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
⇒ P2 (x) = (3x2 − 1)
2
∴ 2P2 (x) = (3x2 − 1)
∴ 2P2 (x) + 1 = 3x2
∴ 2P2 (x) + P0 (x) = 3x2 { 1 = P0 (x)}
2 1
∴ x2 = P2 (x) + P0 (x)
3 3
Now, f (x) = x3 + 2x2 − x − 3
f (x) = x3 + 2x2 − x − 3
2 3 4 2
= P3 (x) + P1 (x) + P2 (x) + P0 (x) − P1 (x) − 3P0 (x)
5 5 3 3
N. B. Vyas Legendre’s Function

27. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex.2 Express x3 − 5x2 + 6x + 1 in
terms of Legendre’s polynomial.
N. B. Vyas Legendre’s Function

28. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex.3 Express 4x3 − 2x2 − 3x + 8 in
terms of Legendre’s polynomial.
N. B. Vyas Legendre’s Function

29. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Generating Function for Pn(x)
∞
1
Pn(x)tn = √
n=0
1 − 2xt + t2
1
= (1 − 2xt + t2)− 2
N. B. Vyas Legendre’s Function

30. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
1
The function (1 − 2xt + t2)− 2 is
called Generating function of
Legendre’s polynomial Pn(x)
N. B. Vyas Legendre’s Function

31. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex Show that
N. B. Vyas Legendre’s Function

32. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex Show that
(i)Pn(1) = 1
N. B. Vyas Legendre’s Function

33. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex Show that
(i)Pn(1) = 1
(ii)Pn(−1) = (−1)n
N. B. Vyas Legendre’s Function

34. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Ex Show that
(i)Pn(1) = 1
(ii)Pn(−1) = (−1)n
(iii)Pn(−x) = (−1)nPn(x)
N. B. Vyas Legendre’s Function

35. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
N. B. Vyas Legendre’s Function

36. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
∞
1
Pn (1)tn = (1 − 2t + t2 )− 2 = (1 − t)−1
n=0
N. B. Vyas Legendre’s Function

37. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
∞
1
Pn (1)tn = (1 − 2t + t2 )− 2 = (1 − t)−1
n=0
∞
1
∴ Pn (1)tn = = 1 + t + t2 + t3 + ...
1−t
n=0
N. B. Vyas Legendre’s Function

38. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
∞
1
Pn (1)tn = (1 − 2t + t2 )− 2 = (1 − t)−1
n=0
∞
1
∴ Pn (1)tn = = 1 + t + t2 + t3 + ...
1−t
n=0
∞ ∞
n
∴ Pn (1)t = tn
n=0 n=0
N. B. Vyas Legendre’s Function

39. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
∞
1
Pn (1)tn = (1 − 2t + t2 )− 2 = (1 − t)−1
n=0
∞
1
∴ Pn (1)tn = = 1 + t + t2 + t3 + ...
1−t
n=0
∞ ∞
n
∴ Pn (1)t = tn
n=0 n=0
Comparing the coefficient of tn both the sides, we get
N. B. Vyas Legendre’s Function

40. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Solution:
∞
1
(i) We have Pn (x)tn = (1 − 2xt + t2 )− 2
n=0
Putting x = 1 in eq(1), we get
∞
1
Pn (1)tn = (1 − 2t + t2 )− 2 = (1 − t)−1
n=0
∞
1
∴ Pn (1)tn = = 1 + t + t2 + t3 + ...
1−t
n=0
∞ ∞
n
∴ Pn (1)t = tn
n=0 n=0
Comparing the coefficient of tn both the sides, we get
Pn (1) = 1
N. B. Vyas Legendre’s Function

41. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
N. B. Vyas Legendre’s Function

42. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
∞
1
Pn (−1)tn = (1 + 2t + t2 )− 2 = (1 + t)−1
n=0
N. B. Vyas Legendre’s Function

43. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
∞
1
Pn (−1)tn = (1 + 2t + t2 )− 2 = (1 + t)−1
n=0
∞
1
∴ Pn (−1)tn = = 1 − t + t2 − t3 + ...
1+t
n=0
N. B. Vyas Legendre’s Function

44. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
∞
1
Pn (−1)tn = (1 + 2t + t2 )− 2 = (1 + t)−1
n=0
∞
1
∴ Pn (−1)tn = = 1 − t + t2 − t3 + ...
1+t
n=0
∞ ∞
∴ Pn (−1)tn = (−1)n tn
n=0 n=0
N. B. Vyas Legendre’s Function

45. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
∞
1
Pn (−1)tn = (1 + 2t + t2 )− 2 = (1 + t)−1
n=0
∞
1
∴ Pn (−1)tn = = 1 − t + t2 − t3 + ...
1+t
n=0
∞ ∞
∴ Pn (−1)tn = (−1)n tn
n=0 n=0
Comparing coefficients of tn , we get
N. B. Vyas Legendre’s Function

46. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(ii) Putting x = −1 in eq(1), we get
∞
1
Pn (−1)tn = (1 + 2t + t2 )− 2 = (1 + t)−1
n=0
∞
1
∴ Pn (−1)tn = = 1 − t + t2 − t3 + ...
1+t
n=0
∞ ∞
∴ Pn (−1)tn = (−1)n tn
n=0 n=0
Comparing coefficients of tn , we get
Pn (−1) = (−1)n
N. B. Vyas Legendre’s Function

47. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
N. B. Vyas Legendre’s Function

48. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
N. B. Vyas Legendre’s Function

49. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
N. B. Vyas Legendre’s Function

50. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
∞
1
Pn (x)(−t)n = (1 + 2xt + t2 )− 2 —(b)
n=0
N. B. Vyas Legendre’s Function

51. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
∞
1
Pn (x)(−t)n = (1 + 2xt + t2 )− 2 —(b)
n=0
from equation (a) and (b)
N. B. Vyas Legendre’s Function

52. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
∞
1
Pn (x)(−t)n = (1 + 2xt + t2 )− 2 —(b)
n=0
from equation (a) and (b)
∞ ∞
n
Pn (−x)(t) = Pn (x)(−1)n (t)n
n=0 n=0
N. B. Vyas Legendre’s Function

53. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
∞
1
Pn (x)(−t)n = (1 + 2xt + t2 )− 2 —(b)
n=0
from equation (a) and (b)
∞ ∞
n
Pn (−x)(t) = Pn (x)(−1)n (t)n
n=0 n=0
Comparing the coefficients of tn , both sides, we get
N. B. Vyas Legendre’s Function

54. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(iii) Now replacing x by −x in eq(1), we get
∞
1
Pn (−x)tn = (1 + 2xt + t2 )− 2 —(a)
n=0
Now, replacing t by −t in eq(1), we get
∞
1
Pn (x)(−t)n = (1 + 2xt + t2 )− 2 —(b)
n=0
from equation (a) and (b)
∞ ∞
n
Pn (−x)(t) = Pn (x)(−1)n (t)n
n=0 n=0
Comparing the coefficients of tn , both sides, we get
Pn (−x) = (−1)n Pn (x)
N. B. Vyas Legendre’s Function

55. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Rodrigue’s Formula
1 dn
Pn(x) = n [(x2 − 1)n]
2 n! dxn
N. B. Vyas Legendre’s Function

56. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
N. B. Vyas Legendre’s Function

57. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
N. B. Vyas Legendre’s Function

58. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
∴ y1 = n(x2 − 1)n−1 (2x)
N. B. Vyas Legendre’s Function

59. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
∴ y1 = n(x2 − 1)n−1 (2x)
2nx(x2 − 1)n 2nxy
∴ y1 = = 2
(x2 − 1) x −1
N. B. Vyas Legendre’s Function

60. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
∴ y1 = n(x2 − 1)n−1 (2x)
2nx(x2 − 1)n 2nxy
∴ y1 = = 2
(x2 − 1) x −1
∴ (x2 − 1)y1 = 2nxy
N. B. Vyas Legendre’s Function

61. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
∴ y1 = n(x2 − 1)n−1 (2x)
2nx(x2 − 1)n 2nxy
∴ y1 = = 2
(x2 − 1) x −1
∴ (x2 − 1)y1 = 2nxy
Differentiating with respect to x,
N. B. Vyas Legendre’s Function

62. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Proof:
Let y = (x2 − 1)n
Differentiating wit respect to x
∴ y1 = n(x2 − 1)n−1 (2x)
2nx(x2 − 1)n 2nxy
∴ y1 = = 2
(x2 − 1) x −1
∴ (x2 − 1)y1 = 2nxy
Differentiating with respect to x,
(x2 − 1)y2 +2xy1 = 2nxy1 + 2ny
N. B. Vyas Legendre’s Function

63. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
N. B. Vyas Legendre’s Function

64. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
dn
→ ((x2 −1)y2 ) = nC0 (x2 −1)yn+2 +nC1 (2x)yn+1 +nC2 (2)yn
dxn
N. B. Vyas Legendre’s Function

65. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
dn
→ ((x2 −1)y2 ) = nC0 (x2 −1)yn+2 +nC1 (2x)yn+1 +nC2 (2)yn
dxn
dn
→ (2xy1 ) = nC0 (2x)yn+1 + nC1 (2)yn
dxn
N. B. Vyas Legendre’s Function

66. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
dn
→ ((x2 −1)y2 ) = nC0 (x2 −1)yn+2 +nC1 (2x)yn+1 +nC2 (2)yn
dxn
dn
→ (2xy1 ) = nC0 (2x)yn+1 + nC1 (2)yn
dxn
dn
→ (2nxy1 ) = nC0 (2nx)yn+1 + nC1 (2n)yn
dxn
N. B. Vyas Legendre’s Function

67. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
dn
→ ((x2 −1)y2 ) = nC0 (x2 −1)yn+2 +nC1 (2x)yn+1 +nC2 (2)yn
dxn
dn
→ (2xy1 ) = nC0 (2x)yn+1 + nC1 (2)yn
dxn
dn
→ (2nxy1 ) = nC0 (2nx)yn+1 + nC1 (2n)yn
dxn
dn
→ (2ny) = 2nyn
dxn
N. B. Vyas Legendre’s Function

68. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn
(U V ) = nC0 U Vn + nC1 U1 Vn−1 + ... + nCn Un V
dxn
dn
→ ((x2 −1)y2 ) = nC0 (x2 −1)yn+2 +nC1 (2x)yn+1 +nC2 (2)yn
dxn
dn
→ (2xy1 ) = nC0 (2x)yn+1 + nC1 (2)yn
dxn
dn
→ (2nxy1 ) = nC0 (2nx)yn+1 + nC1 (2n)yn
dxn
dn
→ (2ny) = 2nyn
dxn
n(n − 1)
Also nC0 = 1, nC1 = n, nC2 =
2!
N. B. Vyas Legendre’s Function

69. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
N. B. Vyas Legendre’s Function

70. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
N. B. Vyas Legendre’s Function

71. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
N. B. Vyas Legendre’s Function

72. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
N. B. Vyas Legendre’s Function

73. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
N. B. Vyas Legendre’s Function

74. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
∴ (1 − x2 )v2 − 2xv1 + n(n + 1)v = 0 ——(2)
N. B. Vyas Legendre’s Function

75. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
∴ (1 − x2 )v2 − 2xv1 + n(n + 1)v = 0 ——(2)
Equation (2) is a Legendre’s equation in variables v and x
N. B. Vyas Legendre’s Function

76. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
∴ (1 − x2 )v2 − 2xv1 + n(n + 1)v = 0 ——(2)
Equation (2) is a Legendre’s equation in variables v and x
⇒ Pn (x) is a solution of equation (2)
N. B. Vyas Legendre’s Function

77. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
∴ (1 − x2 )v2 − 2xv1 + n(n + 1)v = 0 ——(2)
Equation (2) is a Legendre’s equation in variables v and x
⇒ Pn (x) is a solution of equation (2)
Also, v = f (x) is a solution of equation (2)
N. B. Vyas Legendre’s Function

78. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (x2 − 1)yn+2 + 2nxyn+1 + n(n − 1)yn
+2xyn+1 + 2nyn = 2nxyn+1 + n(2n)yn + 2nyn
∴ (x2 − 1)yn+2 + 2xyn+1 + (n2 − n + 2n − 2n2 − 2n)yn = 0
∴ (x2 − 1)yn+2 + 2xyn+1 − n(n + 1)yn = 0
∴ (1 − x2 )yn+2 − 2xyn+1 + n(n + 1)yn = 0
dn y
Let v = yn = n
dx
∴ (1 − x2 )v2 − 2xv1 + n(n + 1)v = 0 ——(2)
Equation (2) is a Legendre’s equation in variables v and x
⇒ Pn (x) is a solution of equation (2)
Also, v = f (x) is a solution of equation (2)
Pn = cv where c is constant
N. B. Vyas Legendre’s Function

79. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
N. B. Vyas Legendre’s Function

80. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
N. B. Vyas Legendre’s Function

81. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
= (x + 1)n (x − 1)n
N. B. Vyas Legendre’s Function

82. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
= (x + 1)n (x − 1)n
dn y dn
∴ = (x + 1)n n ((x − 1)n )
dxn dx
N. B. Vyas Legendre’s Function

83. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
= (x + 1)n (x − 1)n
dn y dn
∴ = (x + 1)n n ((x − 1)n )
dxn dx
dn−1
+n(x + 1)n−1 n−1 ((x − 1)n )
dx
N. B. Vyas Legendre’s Function

84. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
= (x + 1)n (x − 1)n
dn y dn
∴ = (x + 1)n n ((x − 1)n )
dxn dx
dn−1
+n(x + 1)n−1 n−1 ((x − 1)n )
dx
+...
N. B. Vyas Legendre’s Function

85. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
dn y dn
∴ Pn (x) = c = c n (x2 − 1)n ——(3)
dxn dx
Now y = (x2 − 1)n
= (x + 1)n (x − 1)n
dn y dn
∴ = (x + 1)n n ((x − 1)n )
dxn dx
dn−1
+n(x + 1)n−1 n−1 ((x − 1)n )
dx
+...
dn ((x + 1)n )
+ (x − 1)n
dxn
N. B. Vyas Legendre’s Function

86. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
Recurrence Relations for Pn(x) : −
N. B. Vyas Legendre’s Function

87. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
N. B. Vyas Legendre’s Function

88. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
N. B. Vyas Legendre’s Function

89. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
N. B. Vyas Legendre’s Function

90. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
N. B. Vyas Legendre’s Function

91. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
N. B. Vyas Legendre’s Function

92. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
1
= (1 − 2xt + t2 )−1 (1 − 2xt + t2 )− 2 (x − t)
N. B. Vyas Legendre’s Function

93. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
1
= (1 − 2xt + t2 )−1 (1 − 2xt + t2 )− 2 (x − t)
1
(1 − 2xt + t2 )− 2
= (x − t)
(1 − 2xt + t2 )
N. B. Vyas Legendre’s Function

94. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
1
= (1 − 2xt + t2 )−1 (1 − 2xt + t2 )− 2 (x − t)
1
(1 − 2xt + t2 )− 2
= (x − t)
(1 − 2xt + t2 )
from (i)
N. B. Vyas Legendre’s Function

95. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(1) (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
Proof: We have
∞ 1
−
n 2 ) 2 ——–(i)
Pn (x)t = (1 − 2xt + t
n=0
Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
1
= (1 − 2xt + t2 )−1 (1 − 2xt + t2 )− 2 (x − t)
1
(1 − 2xt + t2 )− 2
= (x − t)
(1 − 2xt + t2 )
from (i)
∞ ∞
n−1
(1 − 2xt + t2 ) nPn (x)t = (x − t) Pn (x)tn
n=1 n=0
N. B. Vyas Legendre’s Function

96. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞ ∞
∴ nPn (x)tn−1 − 2x nPn (x)tn + nPn (x)tn+1 =
n=1 n=1 n=1
∞ ∞
x Pn (x)tn − Pn (x)tn+1
n=0 n=0
N. B. Vyas Legendre’s Function

97. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞ ∞
∴ nPn (x)tn−1 − 2x nPn (x)tn + nPn (x)tn+1 =
n=1 n=1 n=1
∞ ∞
x Pn (x)tn − Pn (x)tn+1
n=0 n=0
replacing n by n+1 in 1st term, n by n-1 in 3rd term in
L.H.S.
N. B. Vyas Legendre’s Function

98. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞ ∞
∴ nPn (x)tn−1 − 2x nPn (x)tn + nPn (x)tn+1 =
n=1 n=1 n=1
∞ ∞
x Pn (x)tn − Pn (x)tn+1
n=0 n=0
replacing n by n+1 in 1st term, n by n-1 in 3rd term in
L.H.S.
replacing n by n-1 in 2nd term in R.H.S
N. B. Vyas Legendre’s Function

99. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞ ∞
∴ nPn (x)tn−1 − 2x nPn (x)tn + nPn (x)tn+1 =
n=1 n=1 n=1
∞ ∞
x Pn (x)tn − Pn (x)tn+1
n=0 n=0
replacing n by n+1 in 1st term, n by n-1 in 3rd term in
L.H.S.
replacing n by n-1 in 2nd term in R.H.S
∞ ∞ ∞
(n + 1)Pn+1 (x)tn − 2x nPn (x)tn + (n −
n=0 n=1 n=2
∞ ∞
1)Pn−1 (x)tn = x Pn (x)tn − Pn−1 (x)tn
n=0 n=1
N. B. Vyas Legendre’s Function

100. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞ ∞
∴ nPn (x)tn−1 − 2x nPn (x)tn + nPn (x)tn+1 =
n=1 n=1 n=1
∞ ∞
x Pn (x)tn − Pn (x)tn+1
n=0 n=0
replacing n by n+1 in 1st term, n by n-1 in 3rd term in
L.H.S.
replacing n by n-1 in 2nd term in R.H.S
∞ ∞ ∞
(n + 1)Pn+1 (x)tn − 2x nPn (x)tn + (n −
n=0 n=1 n=2
∞ ∞
1)Pn−1 (x)tn = x Pn (x)tn − Pn−1 (x)tn
n=0 n=1
comparing the coefficients of tn on both the sides
N. B. Vyas Legendre’s Function

101. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (n + 1)Pn+1 (x) − 2xnPn (x) + (n − 1)Pn−1 (x) =
xPn (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

102. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (n + 1)Pn+1 (x) − 2xnPn (x) + (n − 1)Pn−1 (x) =
xPn (x) − Pn−1 (x)
∴ (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − (n − 1 + 1)Pn−1 (x)
N. B. Vyas Legendre’s Function

103. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (n + 1)Pn+1 (x) − 2xnPn (x) + (n − 1)Pn−1 (x) =
xPn (x) − Pn−1 (x)
∴ (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − (n − 1 + 1)Pn−1 (x)
∴ (n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
N. B. Vyas Legendre’s Function

104. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

105. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
N. B. Vyas Legendre’s Function

106. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
N. B. Vyas Legendre’s Function

107. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
N. B. Vyas Legendre’s Function

108. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
∞
1 3
Pn (x)tn = − (1 − 2xt + t2 )− 2 (−2t)
2
n=0
N. B. Vyas Legendre’s Function

109. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
∞
1 3
Pn (x)tn = − (1 − 2xt + t2 )− 2 (−2t)
2
n=0
∞ 1
n t(1 − 2xt + t2 )− 2
∴ Pn (x)t = ————-(ii)
(1 − 2xt + t2 )
n=0
N. B. Vyas Legendre’s Function

110. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
∞
1 3
Pn (x)tn = − (1 − 2xt + t2 )− 2 (−2t)
2
n=0
∞ 1
t(1 − 2xt + t2 )− 2
n
∴ Pn (x)t = ————-(ii)
(1 − 2xt + t2 )
n=0
⇒ Differentiating equation (i) partially with respect to t, we
get
N. B. Vyas Legendre’s Function

111. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
∞
1 3
Pn (x)tn = − (1 − 2xt + t2 )− 2 (−2t)
2
n=0
∞ 1
t(1 − 2xt + t2 )− 2
n
∴ Pn (x)t = ————-(ii)
(1 − 2xt + t2 )
n=0
⇒ Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
N. B. Vyas Legendre’s Function

112. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(2) nPn (x) = xPn (x) − Pn−1 (x)
Proof: We have
∞ 1
−
n
Pn (x)t = (1 − 2xt + t2 ) 2 ——–(i)
n=0
Differentiating equation (i) partially with respect to x, we
get
∞
1 3
Pn (x)tn = − (1 − 2xt + t2 )− 2 (−2t)
2
n=0
∞ 1
t(1 − 2xt + t2 )− 2
n
∴ Pn (x)t = ————-(ii)
(1 − 2xt + t2 )
n=0
⇒ Differentiating equation (i) partially with respect to t, we
get
∞
1 3
nPn (x)tn−1 = − (1 − 2xt + t2 )− 2 (−2x + 2t)
2
n=1
∞ 1
n−1 (x − t)(1 −Legendre’s )− 2
N. B. Vyas
2xt + t2 Function

113. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
N. B. Vyas Legendre’s Function

114. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
N. B. Vyas Legendre’s Function

115. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
∞ ∞ ∞
∴ nPn (x)tn = x Pn (x)tn − Pn (x)tn+1
n=1 n=0 n=0
N. B. Vyas Legendre’s Function

116. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
∞ ∞ ∞
∴ nPn (x)tn = x Pn (x)tn − Pn (x)tn+1
n=1 n=0 n=0
Replacing n by n-1 in 2nd term in R.H.S.
N. B. Vyas Legendre’s Function

117. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
∞ ∞ ∞
∴ nPn (x)tn = x Pn (x)tn − Pn (x)tn+1
n=1 n=0 n=0
Replacing n by n-1 in 2nd term in R.H.S.
∞ ∞ ∞
n n
∴ nPn (x)t = x Pn (x)t − Pn−1 (x)tn
n=1 n=0 n=1
N. B. Vyas Legendre’s Function

118. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
∞ ∞ ∞
∴ nPn (x)tn = x Pn (x)tn − Pn (x)tn+1
n=1 n=0 n=0
Replacing n by n-1 in 2nd term in R.H.S.
∞ ∞ ∞
n n
∴ nPn (x)t = x Pn (x)t − Pn−1 (x)tn
n=1 n=0 n=1
comparing the coefficients of tn on both sides, we get
N. B. Vyas Legendre’s Function

119. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∞ ∞
n−1 (x − t)
nPn (x)t = Pn (x)tn {by eq. (ii)
t
n=1 n=0
∞ ∞
∴ t nPn (x)tn−1 = (x − t) Pn (x)tn
n=1 n=0
∞ ∞ ∞
∴ nPn (x)tn = x Pn (x)tn − Pn (x)tn+1
n=1 n=0 n=0
Replacing n by n-1 in 2nd term in R.H.S.
∞ ∞ ∞
n n
∴ nPn (x)t = x Pn (x)t − Pn−1 (x)tn
n=1 n=0 n=1
comparing the coefficients of tn on both sides, we get
nPn (x) = xPn (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

120. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
N. B. Vyas Legendre’s Function

121. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
N. B. Vyas Legendre’s Function

122. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
N. B. Vyas Legendre’s Function

123. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
N. B. Vyas Legendre’s Function

124. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
N. B. Vyas Legendre’s Function

125. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
Also from relation (2)
N. B. Vyas Legendre’s Function

126. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
Also from relation (2)
nPn (x) = xPn (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

127. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
Also from relation (2)
nPn (x) = xPn (x) − Pn−1 (x)
∴ xPn (x) = nPn (x) + Pn−1 (x)—– (c)
N. B. Vyas Legendre’s Function

128. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
Also from relation (2)
nPn (x) = xPn (x) − Pn−1 (x)
∴ xPn (x) = nPn (x) + Pn−1 (x)—– (c)
Substituting the value of (c) in equation (b), we get
N. B. Vyas Legendre’s Function

129. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(3) (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)n
Proof: We have ( from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
∴ (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x) — (a)
differentiating equation (a) partially with respect to x, We
get
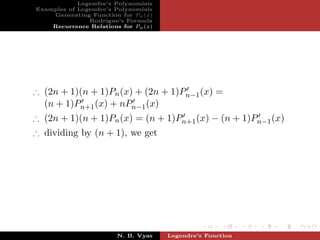
∴ (2n + 1)Pn (x) + (2n + 1)xPn (x) = (n + 1)Pn+1 (x) + nPn−1 (x)
—(b)
Also from relation (2)
nPn (x) = xPn (x) − Pn−1 (x)
∴ xPn (x) = nPn (x) + Pn−1 (x)—– (c)
Substituting the value of (c) in equation (b), we get
∴ (2n + 1)Pn (x) + (2n + 1)[nPn (x) + Pn−1 (x)] =
(n + 1)Pn+1 (x) + nPn−1 (x)
N. B. Vyas Legendre’s Function

130. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (2n + 1)(n + 1)Pn (x) + (2n + 1)Pn−1 (x) =
(n + 1)Pn+1 (x) + nPn−1 (x)
N. B. Vyas Legendre’s Function

131. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (2n + 1)(n + 1)Pn (x) + (2n + 1)Pn−1 (x) =
(n + 1)Pn+1 (x) + nPn−1 (x)
∴ (2n + 1)(n + 1)Pn (x) = (n + 1)Pn+1 (x) − (n + 1)Pn−1 (x)
N. B. Vyas Legendre’s Function

132. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (2n + 1)(n + 1)Pn (x) + (2n + 1)Pn−1 (x) =
(n + 1)Pn+1 (x) + nPn−1 (x)
∴ (2n + 1)(n + 1)Pn (x) = (n + 1)Pn+1 (x) − (n + 1)Pn−1 (x)
∴ dividing by (n + 1), we get
N. B. Vyas Legendre’s Function

133. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
∴ (2n + 1)(n + 1)Pn (x) + (2n + 1)Pn−1 (x) =
(n + 1)Pn+1 (x) + nPn−1 (x)
∴ (2n + 1)(n + 1)Pn (x) = (n + 1)Pn+1 (x) − (n + 1)Pn−1 (x)
∴ dividing by (n + 1), we get
∴ (2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

134. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
N. B. Vyas Legendre’s Function

135. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
N. B. Vyas Legendre’s Function

136. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
N. B. Vyas Legendre’s Function

137. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
N. B. Vyas Legendre’s Function

138. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
N. B. Vyas Legendre’s Function

139. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
Taking (a) - (b), we get
N. B. Vyas Legendre’s Function

140. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
Taking (a) - (b), we get
∴ (n + 1)Pn (x) = Pn+1 (x) − xPn (x)
N. B. Vyas Legendre’s Function

141. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
Taking (a) - (b), we get
∴ (n + 1)Pn (x) = Pn+1 (x) − xPn (x)
replacing n by n − 1, we get
N. B. Vyas Legendre’s Function

142. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
Taking (a) - (b), we get
∴ (n + 1)Pn (x) = Pn+1 (x) − xPn (x)
replacing n by n − 1, we get
∴ nPn−1 (x) = Pn (x) − xPn−1 (x)
N. B. Vyas Legendre’s Function

143. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(4) Pn (x) = xPn−1 (x) + nPn−1 (x)
Proof: We have (from relation (3) ),
(2n + 1)Pn (x) = Pn+1 (x) − Pn−1 (x) —–(a)
Also we have (from relation (2) ),
∴ nPn (x) = xPn (x) − Pn−1 (x) ——(b)
Taking (a) - (b), we get
∴ (n + 1)Pn (x) = Pn+1 (x) − xPn (x)
replacing n by n − 1, we get
∴ nPn−1 (x) = Pn (x) − xPn−1 (x)
∴ Pn (x) = xPn−1 (x) + nPn−1 (x)
N. B. Vyas Legendre’s Function

144. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
N. B. Vyas Legendre’s Function

145. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
N. B. Vyas Legendre’s Function

146. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
N. B. Vyas Legendre’s Function

147. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
N. B. Vyas Legendre’s Function

148. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
N. B. Vyas Legendre’s Function

149. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
xPn (x) = nPn (x) + Pn−1 (x) ——– (b)
N. B. Vyas Legendre’s Function

150. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
xPn (x) = nPn (x) + Pn−1 (x) ——– (b)
taking (a) - x X (b), we get
N. B. Vyas Legendre’s Function

151. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
xPn (x) = nPn (x) + Pn−1 (x) ——– (b)
taking (a) - x X (b), we get
(1 − x2 )Pn (x) = xPn−1 (x) + nPn−1 (x) − nxPn (x) − xPn−1 (x)
N. B. Vyas Legendre’s Function

152. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
xPn (x) = nPn (x) + Pn−1 (x) ——– (b)
taking (a) - x X (b), we get
(1 − x2 )Pn (x) = xPn−1 (x) + nPn−1 (x) − nxPn (x) − xPn−1 (x)
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
N. B. Vyas Legendre’s Function

153. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(5) (1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
Proof: We have (from relation (4) )
Pn (x) = xPn−1 (x) + nPn−1 (x) ——- (a)
also we have (from relation (2) )
nPn (x) = xPn (x) − Pn−1 (x)
xPn (x) = nPn (x) + Pn−1 (x) ——– (b)
taking (a) - x X (b), we get
(1 − x2 )Pn (x) = xPn−1 (x) + nPn−1 (x) − nxPn (x) − xPn−1 (x)
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)]
N. B. Vyas Legendre’s Function

154. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
N. B. Vyas Legendre’s Function

155. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
N. B. Vyas Legendre’s Function

156. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
N. B. Vyas Legendre’s Function

157. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
N. B. Vyas Legendre’s Function

158. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
N. B. Vyas Legendre’s Function

159. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
N. B. Vyas Legendre’s Function

160. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + n[xPn (x) − Pn−1 (x)]
N. B. Vyas Legendre’s Function

161. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + n[xPn (x) − Pn−1 (x)]
n(Pn−1 (x) − xPn (x)) = (n + 1)(xPn (x) − Pn+1 (x))
N. B. Vyas Legendre’s Function

162. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + n[xPn (x) − Pn−1 (x)]
n(Pn−1 (x) − xPn (x)) = (n + 1)(xPn (x) − Pn+1 (x))
from equation (a),
N. B. Vyas Legendre’s Function

163. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + n[xPn (x) − Pn−1 (x)]
n(Pn−1 (x) − xPn (x)) = (n + 1)(xPn (x) − Pn+1 (x))
from equation (a),
(1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
N. B. Vyas Legendre’s Function

164. Legendre’s Polynomials
Examples of Legendre’s Polynomials
Generating Function for Pn (x)
Rodrigue’s Formula
Recurrence Relations for Pn (x)
(6) (1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
Proof: We have (from relation (5) )
(1 − x2 )Pn (x) = n[Pn−1 (x) − xPn (x)] ——(a)
also we have (from relation (1) )
(n + 1)Pn+1 (x) = (2n + 1)xPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + nxPn (x) − nPn−1 (x)
(n + 1)Pn+1 (x) = (n + 1)xPn (x) + n[xPn (x) − Pn−1 (x)]
n(Pn−1 (x) − xPn (x)) = (n + 1)(xPn (x) − Pn+1 (x))
from equation (a),
(1 − x2 )Pn (x) = (n + 1)[xPn (x) − Pn+1 (x)]
N. B. Vyas Legendre’s Function