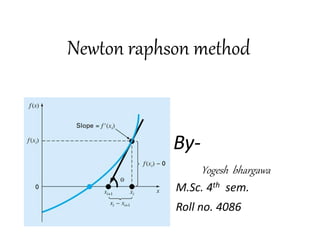
1) Newton Raphson method is a numerical technique used to find roots of algebraic and transcendental equations. It uses successive approximations, starting from an initial guess, to find better approximations for the roots of the equations. 2) The method involves calculating the derivative of the function f(x) and determining the next approximation using the formula xn+1 = xn - f(xn)/f'(xn). 3) An example of finding the root of x3 - 2x - 5 = 0 is shown, starting from an initial guess of 2.5 and iteratively applying the Newton Raphson formula to obtain the root as 2.094551482.

1. Newton raphson method
By-
Yogesh bhargawa
M.Sc. 4th sem.
Roll no. 4086

2. Introduction
As we know from school days , and still we have studied about
the solutions of equations like Quadratic equations , cubical
equations and polynomial equations and having roots in the
form of x=
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
where a, b , c are the coefficient of equ.
But nowadays it is very difficult to remember formulas for higher
degree polynomial equations . Hence to remove these difficulties
there are few numerical methods, one of them is Newton
Raphson Method.
Which has to be discussed in this power point presentation.

3. Newton Raphson Method :
Newton Raphson method is a numerical technique
which is used to find the roots of Algebraic & transcendental
Equations .
Algebraic Equations :
An equation of the form of quadratic or polynomial.
e.g. 𝑥4+𝑥2+1=0
𝑥8-1 =0
𝑥3-2x -5=0

4. Transcendental equation :
An equation which contains some transcendental functions
Such as exponential or trigonometric functions.
e.g. sin , cos , tan , 𝑒 𝑥 , 𝑥 𝑒 , log etc.
3x-cosx-1=0
logx+2x=0
𝑒 𝑥
-3x=0
Sinx+10x-7=38

5. Newton Raphson Method :
Let us consider an equation f(x)=0 having graphical representation as

6. • f(x) =0 ,is an given equation
• Starting from an initial point 𝑥0
• Determine the slope of f(x) at x=𝑥0 .Call it f’(𝑥0).
Slope =tanѲ=
𝑓(𝑥 𝑖)−0
𝑥 𝑖−𝑥 𝑖+1
= 𝑓′ 𝑥𝑖 .
From here we get
• f’(𝑥𝑖) =
𝑓(𝑥 𝑖)
𝑥 𝑖−𝑥 𝑖+1
.
Hence ;
• 𝐱 𝐢+𝟏 = 𝐱 𝐢 −
𝐟(𝐱 𝐢)
𝐟′(𝐱 𝐢)
• Newton Raphson formula

7. Algorithm for f(x)=0
• Calculate f’(x) symbolically.
• Choose an initial guess 𝑥0as given below
let [a,b] be any interval such that f(a)<0 and f(b)>0 , then
𝑥0=
𝑎+𝑏
2
.
• then 𝑥1 = 𝑥0 −
𝑓 𝑥0
𝑓′ 𝑥0
.
• Similarly 𝑥2 = 𝑥1 −
𝑓 𝑥1
𝑓′(𝑥1)
.
• Then by repetition of this process we can find 𝑥3 , 𝑥4 , 𝑥5 … …
• At last we reach at a stage where we find 𝒙𝒊+𝟏 = 𝒙𝒊.
• Then we will stop.
• Hence 𝒙𝒊 will be the required root of given equation.

8. NRM by Taylor series :
if we have given an equation f(x)=0.
𝑥0 be the approximated root of given equation.
• Let (𝑥0 +h) be the actual root where ‘h’ is very small such that
• f(𝑥0 + ℎ)=0
From Taylor series expansion on expanding to f(𝑥0 + ℎ)
f(𝑥0 + ℎ)=f(𝑥0) + hf’(𝑥0)+
ℎ2
2!
f’’(𝑥0) +
ℎ3
3!
f’’’(𝑥0) +…….
Now on neglecting higher powers of h
• f(𝑥0) + hf’(𝑥0) =0
From above h= -
𝑓(𝑥0)
𝑓′(𝑥0)
Cont..

9. Hence first approximation 𝑥1=(𝑥0 + ℎ);
𝑥1=𝑥0-
𝑓(𝑥0)
𝑓′(𝑥0)
Second approximation ;
𝑥2=𝑥1-
𝑓(𝑥1)
𝑓′(𝑥1)
On repeating this process
We get
𝒙 𝒏+𝟏=𝒙 𝒏 −
𝒇(𝒙 𝒏)
𝒇′(𝒙 𝒏)
This is the required newton Raphson method.

10. How to solve an example :
F(x)= 𝑥3
- 2x – 5
F’(x) = 3𝑥2-2
Now checking for initial point
F(1) =-6
F(2)= -1
F(3) =16
Hence root lies between (2,3)
Initial point (𝑥0) =
2+3
2
=2.5
From NRM formula
𝑥 𝑛+1=𝑥 𝑛 −
𝑓(𝑥 𝑛)
𝑓′(𝑥 𝑛)
,putting all these above values in this formula

11. 𝑥 𝑛+1 = 𝑥 𝑛 −
On putting initial value 𝑥0 = 2.5
We get first approximate root;
𝑥1=2.164179104
Similarly:
𝑥2=2.097135356
𝑥3=2.094555232
𝑥4=2.094551482
𝑥5=2.094551482
Hence 𝐱 𝟒=𝐱 𝟓
Hence 2.094551482 is the required root of given equation.
23
52
2
3


n
nn
x
xx

12. Application of NRM
• To find the square root of any no.
• To find the inverse
• To find inverse square root.
• Root of any given equation.

13. Limitations of NRM
• F’(x)=0 is real disaster for this method
• F’’(x)=0 causes the solution to diverse
• Sometimes get trapped in local maxima and minima .

14. THANK YOU..!!!!!!