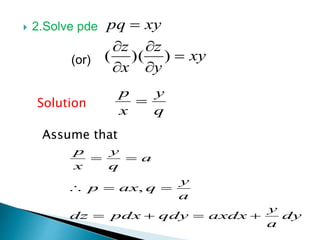
The document discusses partial differential equations (PDEs). It defines PDEs and gives their general form involving independent variables, dependent variables, and partial derivatives. It describes methods for obtaining the complete integral, particular solution, singular solution, and general solution of a PDE. It provides examples of types of PDEs and how to solve them by assuming certain forms for the dependent and independent variables and their partial derivatives.

2.  It is defined as an equation involving two or
more independent variables like x,y……., a
dependent variable like u and its partial
derivatives.
 Partial Differential Equation can be formed
either by elimination of arbitrary constants
or by the elimination of arbitrary functions
from a relation involving three or more
variables .

3.  The general form of a first order partial
differential equation is
z

z

F x y z p q
F x y z
( , , , , )  ( , , , , )  0......(1)
y

x

where x, y are two independent variables, z
is the dependent variable and p = zx and
q = zy

4. 1) COMPLETE INTEGRAL SOLUTION
2) PARTICULAR SOLUTION
3) SINGULAR SOLUTION
4) GENERAL SOLUTION

5.  Let
z

z

F x y z p q
F x y z
( , , , , )  ( , , , , )  0......(1)
y

x

be the Partial Differential Equation.
 The complete integral of equation (1) is
given by
 (x, y, z,a,b)  0.........(.2)
 where a and b are two arbitrary constants

6.  A solution obtained by giving the particular
values to the arbitrary constants in a complete
integral is called particular solution.

7.  It is the relation between those specific
variables which involves no arbitrary
constant and is not obtainable as a
particular integral from the complete
integral.
 So, equation is
x y z a b
 

( , , , , ) 0

0, 
0





a b

8.  A relation between the variables involving
two independent functions of the given
variables together with an arbitrary function
of these variables is a general solution.
 In this given equation
 (x, y, z,a,b)  0.........(.2)
assume an arbitrary relation of form
b  f (a)

9.  So, our earlier equation becomes
 (x, y, z,a, f (a))  0.........3()
 Now, differentiating (2) with respect to a
and thus we get,
( )  0.........(.4)
 


a 
b


f a
 If the eliminator of (3) and (4) exists, then it
is known as general solution.

10.  TYPE-1
The Partial Differential equation of the form
has solution
f ( p,q)  0
z  ax by  c and
f (a,b)  0

11.  TYPE-2
The partial differentiation equation of the form
z  ax by  f (a,b)
is called Clairaut’s form of partial differential
equations.

12.  TYPE-3
 If the partial differential equations is given
by
f (z, p,q)  0
 Then assume that
z  
x 
ay
( )
u  x 
ay
z 
u
( )


13. dz
dz
du
z


z


1 .
a a
u
u

u
y
z


z


u
z


z


y
q
du
u
x
u
x
p











.

14.  TYPE-4
 The partial differential equation of the given
form can be solved by assuming
f ( x , p )  g ( y , q )

a
f x p a p x a
( , )   

( , )
g y q a q y a
( , )    
( , )
z


dy
y
z


dx
x
dz


dz  
( x , a ) dx ( y , a )
dy

15. p2  q 1
 1.Solve the pde and find the
complete and singular solutions
 Solution
Complete solution is given by
z  ax by  c
 with
1
1
2
2
a b
 
b a
  

16. z  ax  (a 1) y  c 2
d.w.r.to. a and c then
2
 
1 0
z

z


 

c
x ay
a
Which is not possible
Hence there is no singular solution

17.  2.Solve pde
pq xy
z
z


(or) xy
y
x




( )( )
Solution
y
q
p
x

Assume that
dy
y
a
y
a
a
y
 
q
p ax q
p
x
  ,

dz pdx qdy axdx
   

18.  Integrating on both sides
b
2 2
x y
z  a  
a
2 2

19. 130080112013
130080112014
130080112015
130080112016
130080112017