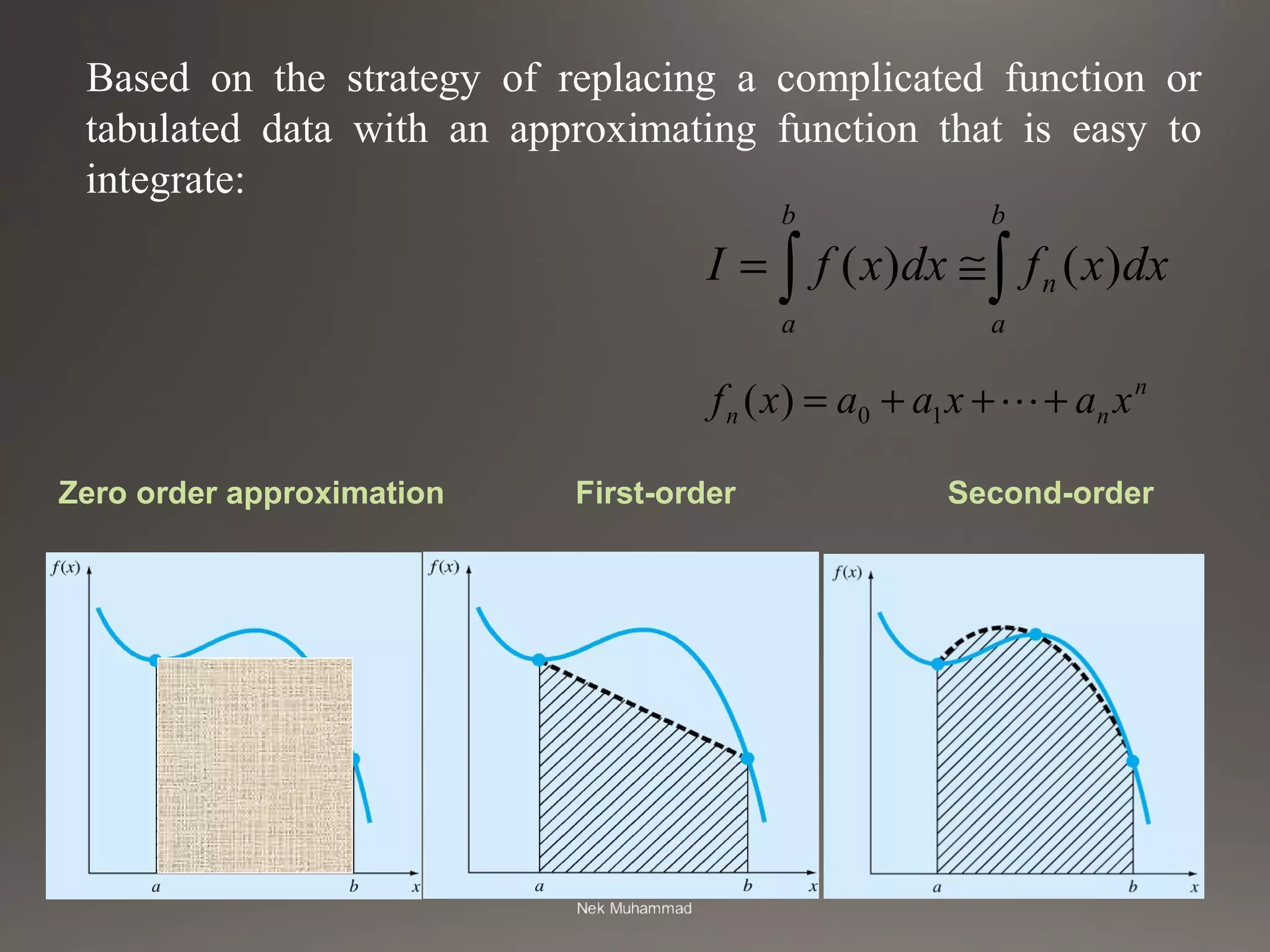
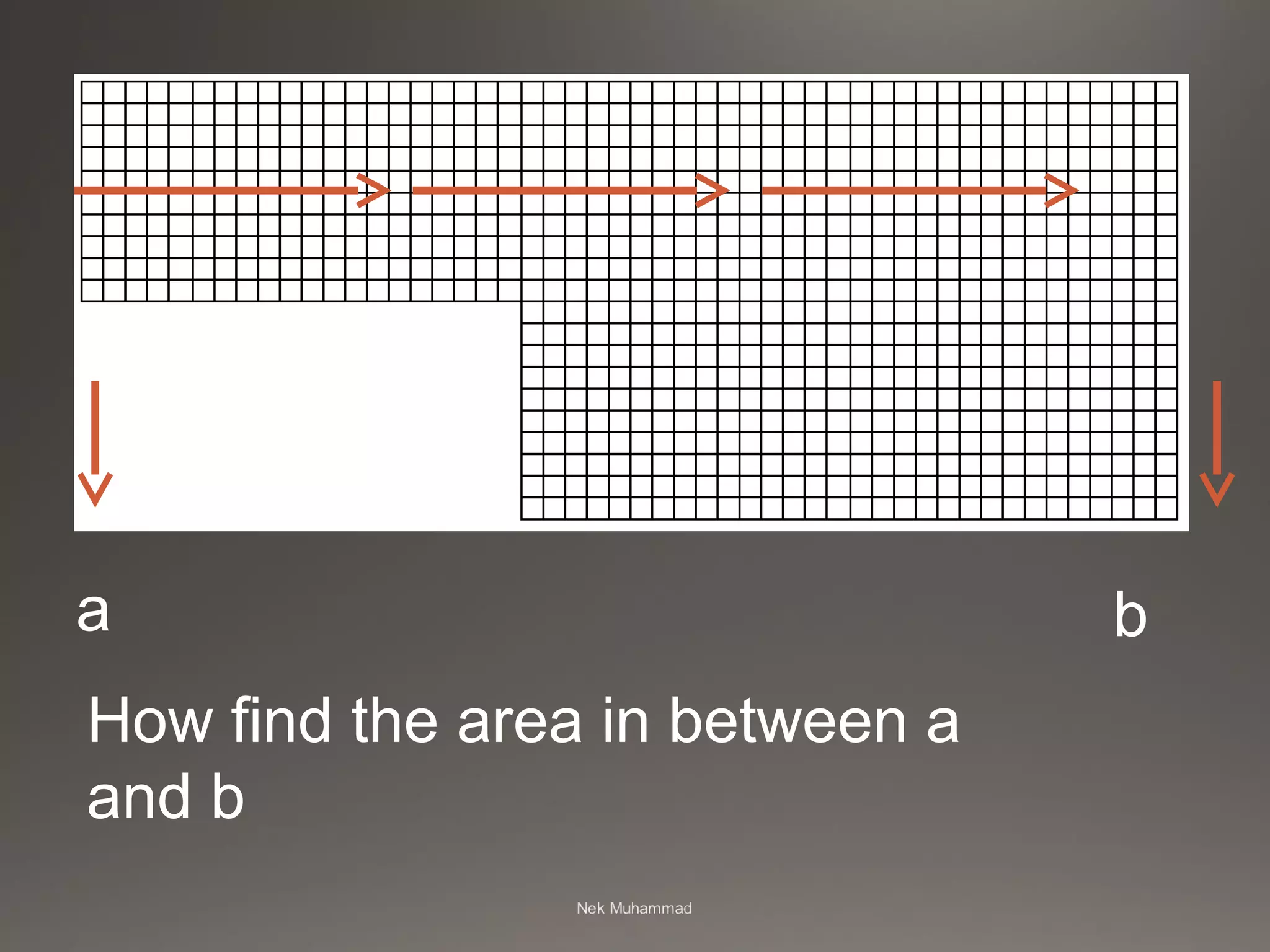
This document provides an introduction and overview of numerical analysis. It begins by stating that numerical analysis aims to find approximate solutions to complex mathematical problems through repeated computational steps when analytical solutions are not available or practical. It then discusses that numerical analysis is important because it allows for the conversion of physical phenomena into mathematical models that can be solved through basic arithmetic operations. Finally, it explains that numerical analysis involves developing algorithms and numerical techniques to solve problems, implementing those techniques using computers, and analyzing errors in approximate solutions.

1. Numerical AnalysisNumerical Analysis
Nek Muhammad katpar
Assistant Professor (maths)
Department of BSRS
MUET SZAB KHAIRPUR

2. Aims and ObjectivesAims and Objectives
After completing this course you should be able
to:
1.Understand the importance of numerical
analysis;
2.Learn the development of Mathematical
Models related to Engineering and Science
problems;
3.Apply various methods in different fields of
Engineering.

3. IntroductionIntroduction
In real world how the solutions of any physical
problems can be obtained?
Two ways to find the solution of physical
problems in real world:
1.Experimental:
•Laboratory experiments;
•Field observations / Study;

4. IntroductionIntroduction
Experimental studies (both Laboratory and
Field Observations) are very expensive, time
consuming and specific (parameter dependent);
2.The alternate way is mathematical solution.
Mathematical solution can be obtained in two
ways, i.e., Analytical methods and numerical
Methods.

5. IntroductionIntroduction
Mathematical Solutions:
•Analytical technique have exact solution;
•Available for only simple problems;
•May not be available for complex problems;
•Very cheap and cost effective.
•Only simple mathematical problems can be
solved.

6. What are numerical methods and
why should you study them?

7. What are numerical methods and
why should you study them?

8. What are numerical methods and
why should you study them?

9. What are numerical methods and
why should you study them?

10. What are numerical methods and
why should you study them?

11. What are numerical methods and
why should you study them?

12. What are numerical methods and
why should you study them?

13. What are numerical methods and
why should you study them?

14. What are numerical methods and
why should you study them?

15. What are numerical methods and
why should you study them?

16. What are numerical methods and
why should you study them?
16

19. Zero order approximation First-order Second-order
Based on the strategy of replacing a complicated function or
tabulated data with an approximating function that is easy to
integrate:
∫∫ ≅=
b
a
n
b
a
dxxfdxxfI )()(
)( 10
n
nn xaxaaxf +++= 

20. a b
To find the area in between a
and b where
A = 0 and b = 125 cm and
space of each line is h = 1 or
0.5 or 0.1

21. a b
How find the area in between a
and b

22. There are two ways
•Either use Laboratory instruments to
the area of whole length of the geometry
•Either use numerical methods to find
the area of small rectangles/squares
then sum of all rectangle or squares

23. ba

25. IntroductionIntroduction
In real world many physical problems are
complex for which analytical solution may not
be available or may be so complex that they
are quite unsuitable for practical purposes. In
this situation, the only alternate way is to
approximate the problem. The approximate
solution can be obtained through automatic
computation to a repetition process of series of
steps. Such process is known as numerical
methods and the analysis of such methods is
called Numerical Analysis.

26. IntroductionIntroduction
The subject of numerical analysis is concerned
with the derivation, construction of algorithm,
implementation and analysis of method for
finding optimal approximate / numerical
solution to complex mathematical problems up
to desire (given) degree of numerical accuracy.

27. Which Mathematical
problems are; that is not
solved analytically
?
?
?

28. IntroductionIntroduction
What is numerical analysis?
• Branch of science which deal with numbers
and algebraic operations, and repeated
steps;
• Art to design algorithm;
• Involves engineering and physics.

29. IntroductionIntroduction
Why numerical analysis?
• Converting a physical phenomenon into
mathematical model;
• When exact/analytical solution or close form
is not available;
• Complex problems can be solved with simple
arithmetic operations;

30. Why numerical analysis?Why numerical analysis?
• Numerical analysis involves mathematics in
developing techniques for the approximate
solution of the mathematical equations
describing the model and involves basic
arithmetic operations.
• Finally, numerical analysis involves
computer science for the implementation of
these techniques in a optimal fashion for the
particular computer.

31. Numerical MethodsNumerical Methods
Main aim / objective of numerical methods is to
provide practical procedure for calculating the
approximate solution of problems in applied
mathematics to a specified degree of accuracy.
It is study of relations that exist between the
values assumed by the function when ever the
independent variable changes by finite jumps
whether equal or unequal.

32. Numerical MethodsNumerical Methods
Main aim / objective of numerical methods is to
provide practical procedure for calculating the
approximate solution of problems in applied
mathematics to a specified degree of accuracy.
It is study of relations that exist between the
values assumed by the function when ever the
independent variable changes by finite jumps
whether equal or unequal.

33. Error AnalysisError Analysis
What is error?
Definition: An error is basically the deflection
of computed/estimated/observed values from
actual/computed/targeted values .
In other words error is a difference between
actual and computed values.

34. Error AnalysisError Analysis
Errors analysis is the study of estimation of
accuracy of the approximate solution with
exact solution and suggest the ways to
eliminate or minimise difference or
enhancement of the accuracy. Estimation of
error is used to find the optimal numerical
solution.

35. Error AnalysisError Analysis
Here various types of errors are discussed,
there source and the nature of their
propagation.
Sources of errors:
In many computational techniques there is the
requirement of precision of significant figures.
The significant figure is a number that carries
real information about the magnitude of
number.

36. Error AnalysisError Analysis
Some times in calculations we approximate
values, so as to make the values smaller than
their original size thus making calculations
much more simplified.
This process may be very useful, but it causes
the errors to occur. Errors in computational
field are surplus to requirements. Because of
this first of all we analyse the errors and than
seek to avoid them in the best possible manner.
36

37. Error AnalysisError Analysis
Types of error:
Errors are classified as follows:
•Gross errors;
•Round off error;
•Truncation error;
•Inherent error;
•Absolute error;
•Relative absolute percentage error;
•Root mean square error;

38. Error AnalysisError Analysis
GROSS ERRORS:
Not directly related with most of the numerical
methods, may have great impact on the success
of modelling efforts. Examples of this type of
error are: use of inaccurate data, mathematical
formulae, algorithm and mishandling of in the
interchanging of neighbouring digits.

39. Error AnalysisError Analysis
ROUND OFF ERRORS:
These errors are unavoidable in most of the
calculations since some of the quantities in the
calculations will be non-terminating decimal
places and for practical reasons only certain
number of will be carried in calculations. These
are due to the fact that in computational work
we have to deal with approximations.

40. Error AnalysisError Analysis
TRUNCATION ERRORS:
These are caused by the use of a closed form,
such as the first few terms of an infinite series
to express a quantity defined by the limiting
process. For example, such errors occur when
a definite integral is computed by Simpson’s
rule or when a differential equation is solved
by some difference method.

41. Error AnalysisError Analysis
PROPAGATION OR INHERENT ERRORS:
These errors are due to the approximate
nature of the applied formulae used in the
solution. It is caused by the use of previous
points calculated by the computer which
already has errors owing to the two errors
above since we are already off the solution
curve, we cannot expect any new points we
compute it to be the correct solution curve.

42. Error AnalysisError Analysis
Some definitions: Before proceeding further, it
would be constructive to have knowledge about
some following terms
•Significant digits;
•Precision and accuracy;
•Absolute, relative and percentage;

43. Significant digitsSignificant digits
A significant digits in an approximate number
is a digit, which provides reliable information
regarding the magnitude of number.
Alternatively, a significant digit is used to
express accuracy, i.e., how many digits are
meaningful in the number.

44. Significant digitsSignificant digits
Rules for significant digits:
•Leading zeros are not significant; The no.
0.0002025 has four significant digits.
•Following zeros that appear after the decimal
point are significant; The no. 0.00202570 has
six significant digits.

45. Significant digitsSignificant digits
• Following zeros that appear before the
decimal point may or may not be
significant, as more information is
required for decision; 202570 has four,
five, six or seven significant digits
depending upon the situation.
• The significant digit in a number do not
depend on the position of the decimal point
in the number; The no. 12456 and .12456
both contain five significant digits.

46. Precision and AccuracyPrecision and Accuracy
Precision and Accuracy are often confusing !!
Precision is the number of digits in which a
number is expressed.
Accuracy is the number of digits to which
solution is correct: to a given number of
decimal places or significant figures.

47. Numerical AnalysisNumerical Analysis
In numerical analysis the robustness of the
numerical algorithm depends on the accuracy
of the approximate numerical solution,
convergence and stability of the numerical
method has always of great importance.

48. Error AnalysisError Analysis
ABSOLUTE ERRORS:
The absolute error of number, measurement,
or calculation is the numerical difference
between the true value of the quantity and its
approximate value as given or obtained by
measurement or calculation. If Xa and Xc are
respectively the actual and computed solution
of a quantity, then the absolute error (AE) is
define by, a cAE X X= −

49. Error AnalysisError Analysis
RELATIVE ERRORS:
The relative error is the absolute error divided
by the true value of the quantity or ration of
absolute error and actual solution. Then the
relative error (RE) is define by,
; 0.
a
AE
aX
RE X= ≠