The bisection method is a straightforward root-finding technique that divides an interval and selects subintervals where a root may exist, providing slower but guaranteed convergence to a solution, given the function is continuous. The document details the method's procedure, including steps for selecting intervals, midpoint calculations, and iterative approximation, also noting its limitations such as slow convergence and inability to handle complex roots. Examples demonstrate application and comparison between analytical and programming results, highlighting its advantages and disadvantages.

1. Bisection Method
By:
Ankit
Choudhary
Ankush Rathore
Anuj Yadav

2. The Bisection Method in mathematics is a root finding
method which repeatedly bisects an interval and then selects
a subinterval in which a root must lie for further processing.
INTRODUCTION

3.  It is a very simple method, but it is also relatively
slow. Because of this, it is often used to obtain a
rough approximation to a solution which is then used
as a starting point for more rapidly converging
methods.
 Bisection method is also called Interval halving
method

4. Graphical
Representation

6. Procedure of Bisection Method
 Step 1: Choose two approximations a and b
such that,
f(a)*f(b)<0
 Step 2: Evaluate the midpoint c of [a,b]
given by,
c=(a+b)/2

7.  Step 3 : If f(c)*f(b)<0
then rename b & c as a & b. If not rename of c as b,
Then apply the formula of Step 2.
 Step 4: Stop evolution when the different of two
successive values of c obtained from Step 2 is
numerically less than e, the prescribed accuracy

8. If the function f (x) changes sign between the two
points, more than one root for the equation f (x) = 0
may exist between the two points.

9. If the function f (x) does not change sign between two points,
there may not be any roots for the equation f (x) = 0 between
the two points.

10. If the function f (x) does not change sign between the two
points, roots of the equation f (x) = 0 may still exist
between the two points.

11. FLOWCHART

12. Start
Input : a,
b
f(a)*f(b) < 0 Try with another
values of a, b
f(a)*f(x) <
0
b = x
a = x
|f(x)| <
tolr
Yes
x=(a+b)/2
Yes
Yes
Outpu
t : root
= x
No
No
No

13. PROGRAM CODE AND OUTPUT

15. input the values of a and b such that f(a) and f(b) have opposite values
0
1
the Root of Function f(x)= 0.567143440
the Root of Function f(x)= 0.567142963
the Root of Function f(x)= 0.567143202
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143261
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143321
the Root of Function f(x)= 0.567143321

17. input the values of a and b such that f(a) and f(b) have opposite values
0
1
the Root of Function f(x)= 0.656620502
the Root of Function f(x)= 0.656620264
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620324
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620383
the Root of Function f(x)= 0.656620383

18. input the values of a and b such that f(a) and f(b) have opposite values
1
2
the Root of Function f(x)= 1.83424330
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424318
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306
the Root of Function f(x)= 1.83424306

19. input the values of a and b such that f(a) and f(b) have opposite values
-2
-3
the Root of Function f(x)= -2.49086356

20. ANALYTICAL SOLUTION OF ROOTS

21. (a) To find roots of equation with the help
of calculator using bisection method

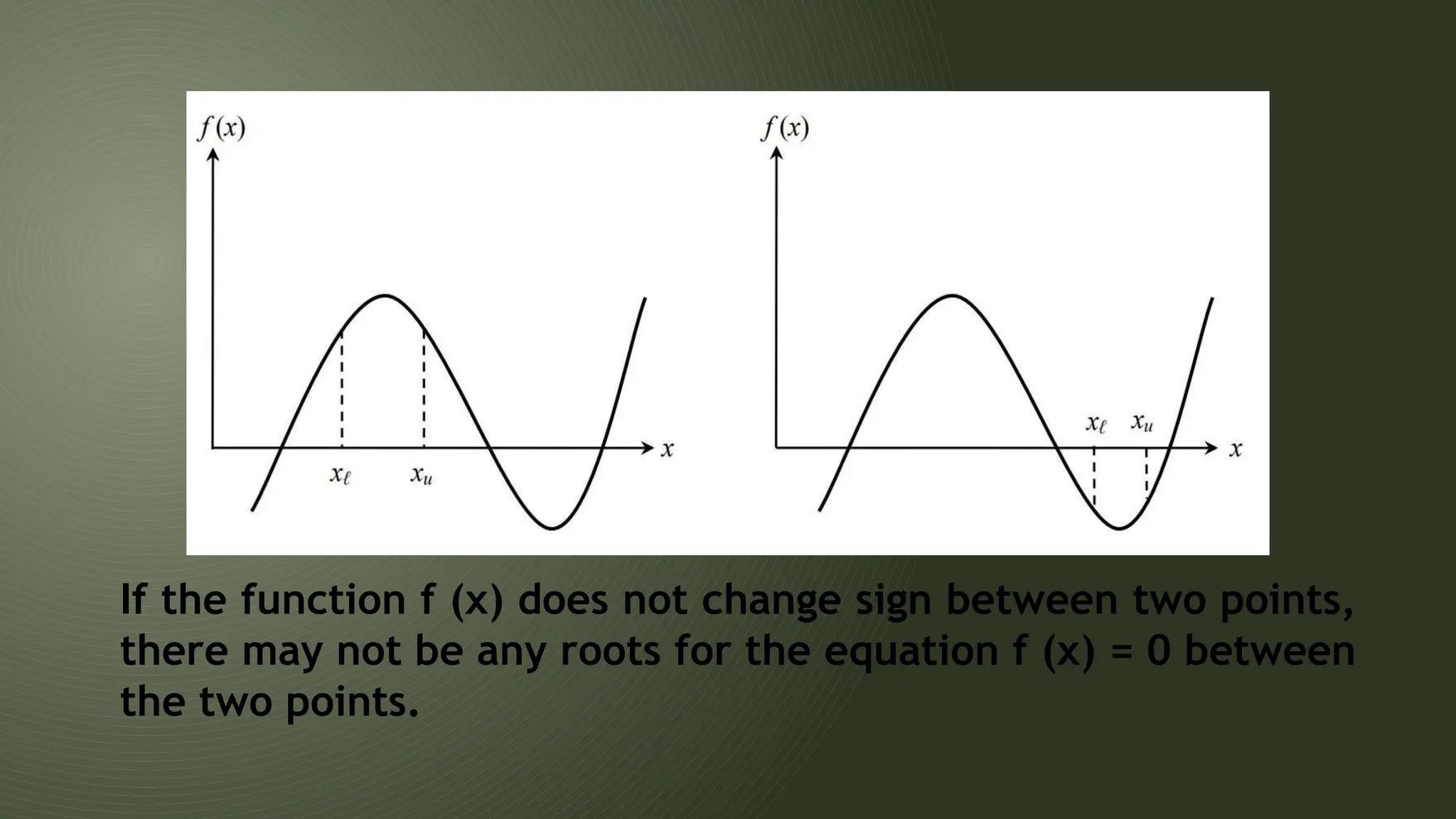
22.  x*exp(x)-1=0
Let f(x)=x*exp(x)-1
f(0)=0-1=-1
f(1) = 1.e-1=1.7182
So, the root lies in [0,1]
a = 0, b = 1
first iteration
x1 = (0 + 1)/2 = 0.5
f(x1)=f(0.5) = (0 .5)exp(0.5)-1= -0.175639
Here f(x1)*f(b)< 0
f(0.5)*f(1)< 0
So, x1 = a = 0.5
New interval [ 0.5,1]

23. Second iteration
x2 = (0.5+1)/2 = 0.75
f(x2)=f(0.75) = 0.5877
Here f(x2)*f(a)< 0
So, x2 = b = 0.75
New interval [ 0.5, 0.75]

24. Similarly, x3=0.625 [0.5 , 0.625]
x4=0.5625 [0.5625, 0.625]
………………………………………
……………………………………
………………………………………
x12=0.56713855
here x12=0.56714 (to five decimal places)
so , the root of equation f(x) is 0.56714

25.  x**3-5*x+3=0
Let f(x) = x**3- 5x + 3
f(0)=0-5(0)+3= +3
f(1) = 1 - 5 + 3 = -1
So, the root lies in [0,1]
a = 0, b = 1
first iteration
x1 = (0 + 1)/2 = 0.5
f(x1)=f(0.5) = (0 .5)**3 - 5(0.5) + 3 = 0.625
Here f(x1)*f(b)< 0
f(0.5)*f(1) <0,
So, x1 = a = 0.5
New interval [ 0.5,1]

26.  Second iteration
x2 = (0.5+1)/2 = 0.75
f(x2)=f(0.75) = (0.75)**3 - 5(0.75) + 3 = -0.328125
Here f(x2)*f(a)< 0
f(0.75)*fa) <0,
So, x2 = b = 0.75
New interval [ 0.5, 0.75]

27. Similarly, x3=0.625 [0,625, 0.75]
x4=0.6875 [0.625, 0.6875]
………………………………………
……………………………………
………………………………………
x20=0.65662075
x21=0.65662025
Here x20 ~ x21 (to six decimal places)
So, the root of equation f(x) is 0.656620

28. (c) GRAPHICAL VERIFICATION OF THE
ROOTS

29. x*exp(x)-1=0

30. X**3-5*x+3=0

31. Result
 The root of the given equation by Fortran
programming and by alytical solution is
almost same.
Equation (1) x**3-5*x+3=0
x=0.656620
Equation (2) x*exp(x)-1=0
x=0.56714

32. Error Analysis
 Error %%
for, xexp(x)-1=0
Error % =0.000004%
for, x**3-5*x+3=0
Error % =0.00005%

33. ADVANTAGES
 The bisection method is very simple and easy to program on the computer.
 Does not involve complex calculations.
 The bisection method guarantees converges to a root in an interval as long as
the function is continuous

34. DISADVANTAGES
 This method is very slow i.e. we have to do many steps
to get the root of desired accuracy(slow to
convergence)
 It fails to determine complex roots.
 It can not be applied if there are discontinuities in the
guess interval.

35. THANK YOU