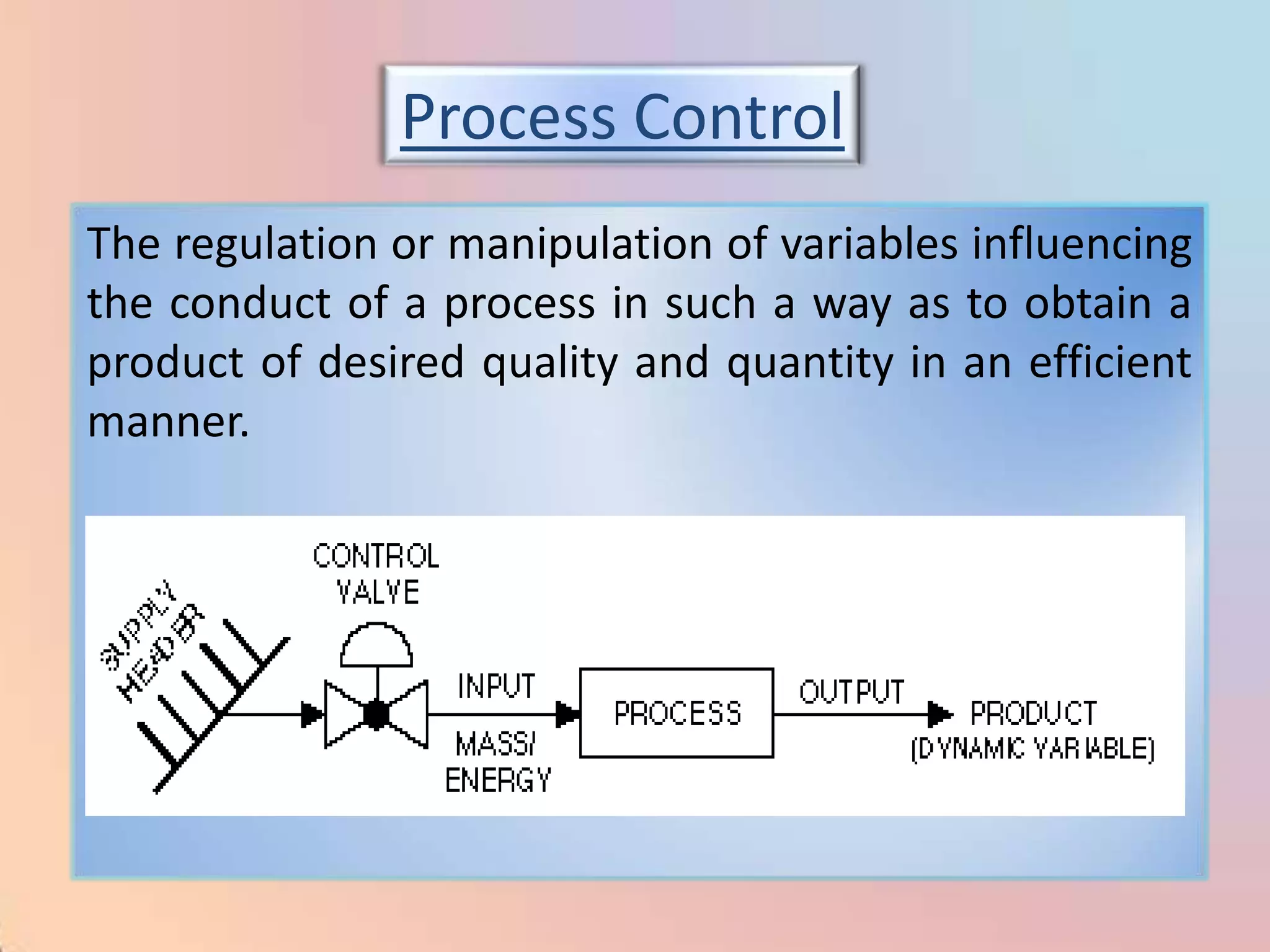
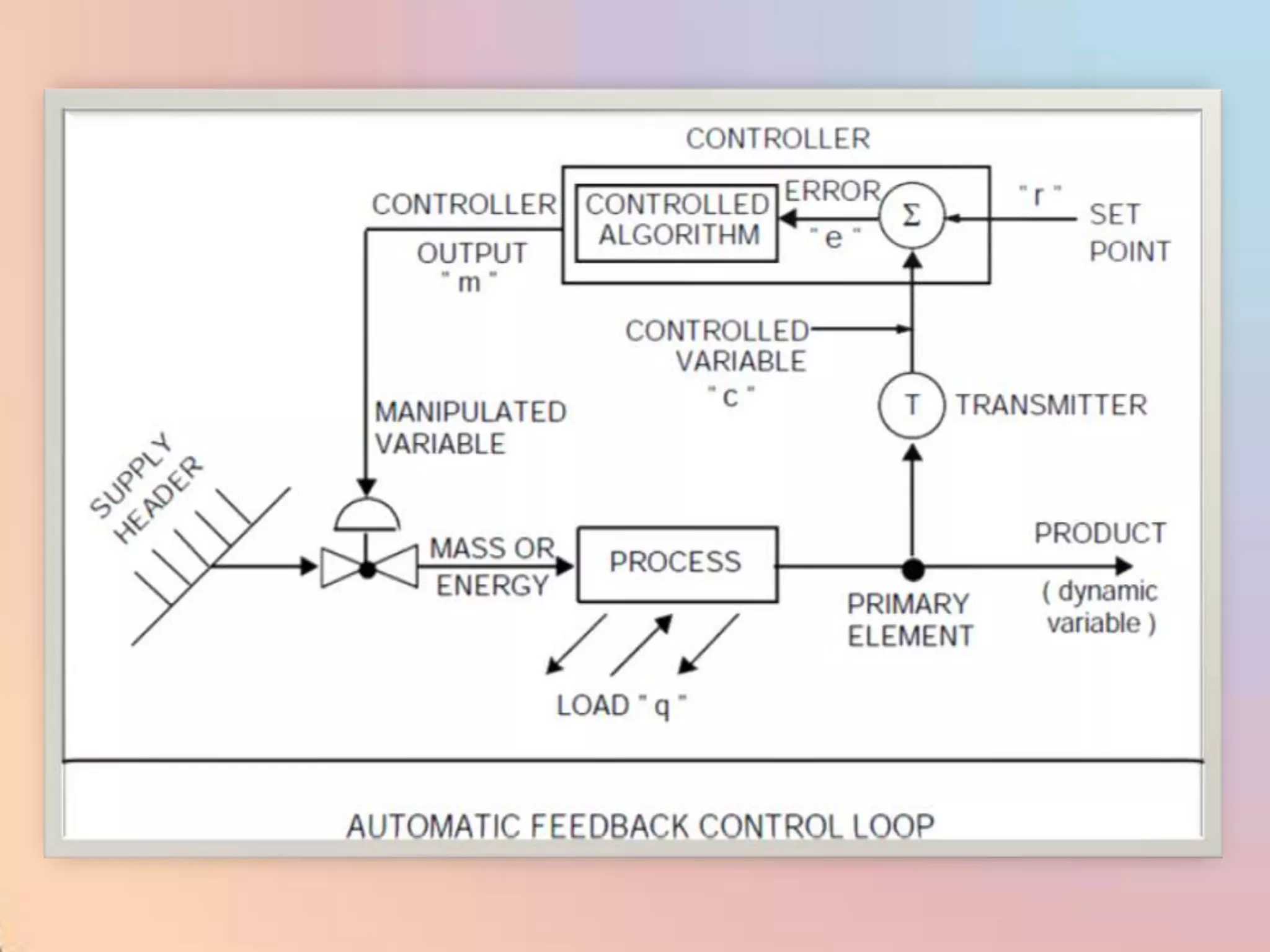
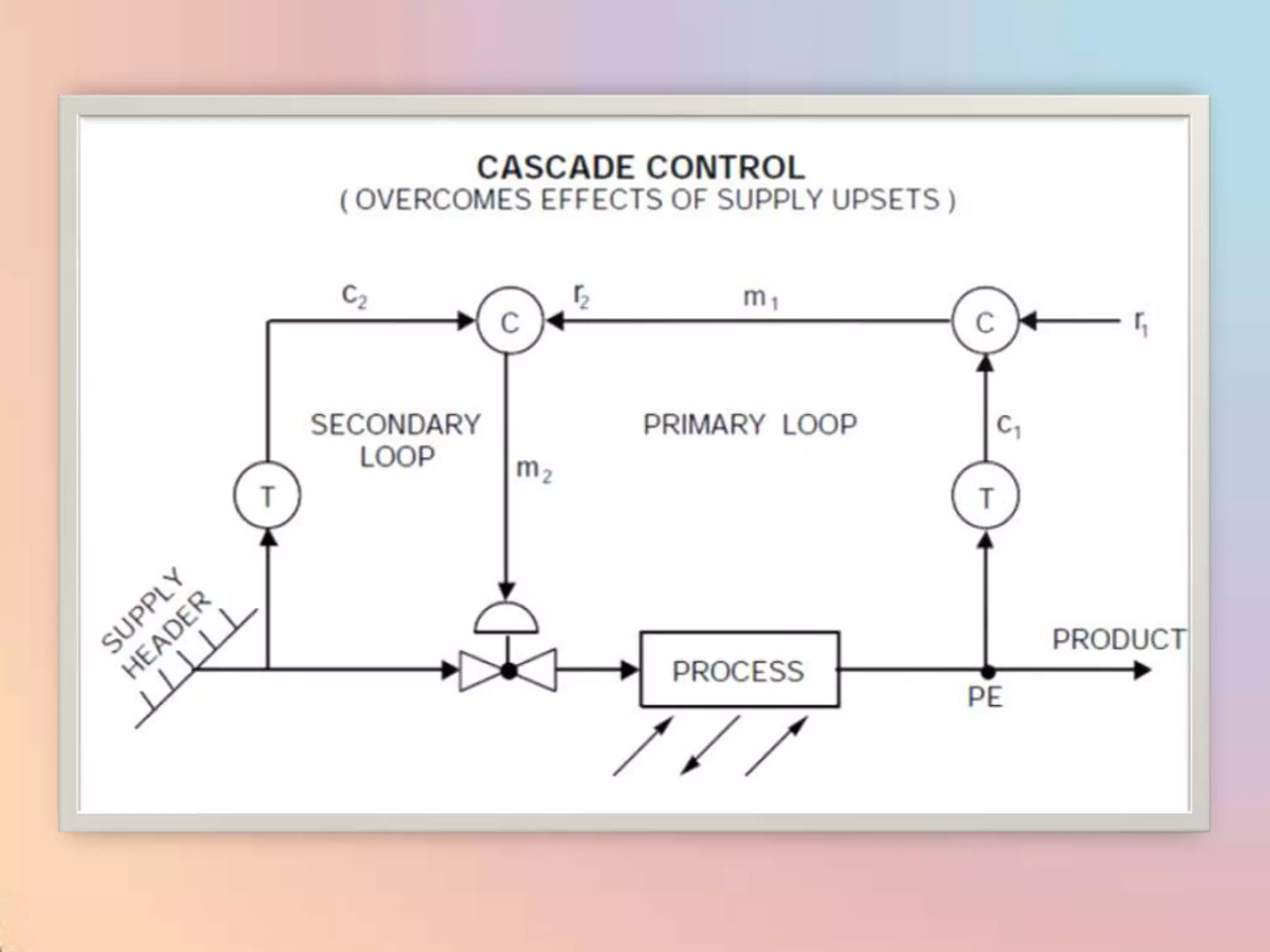
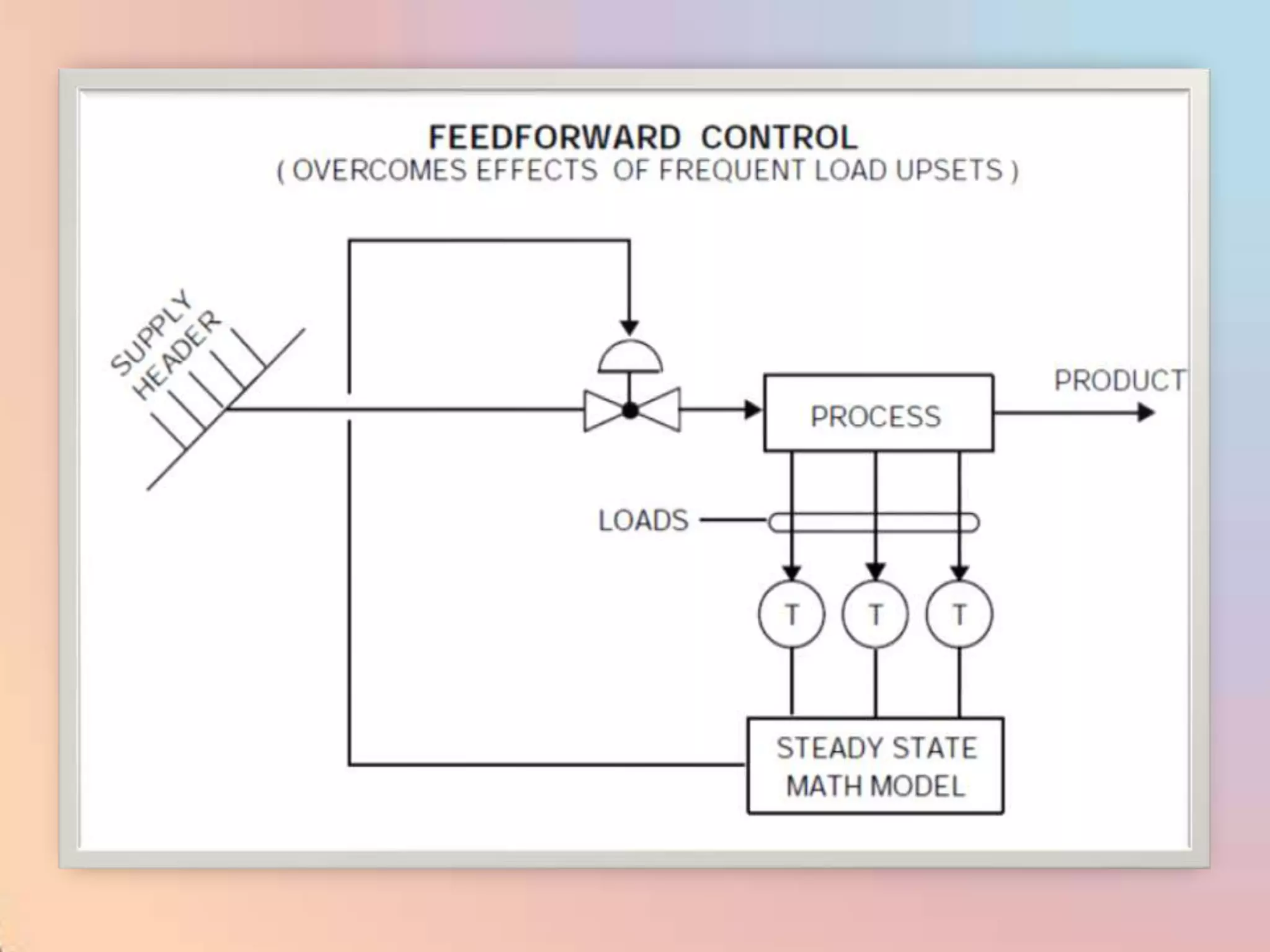
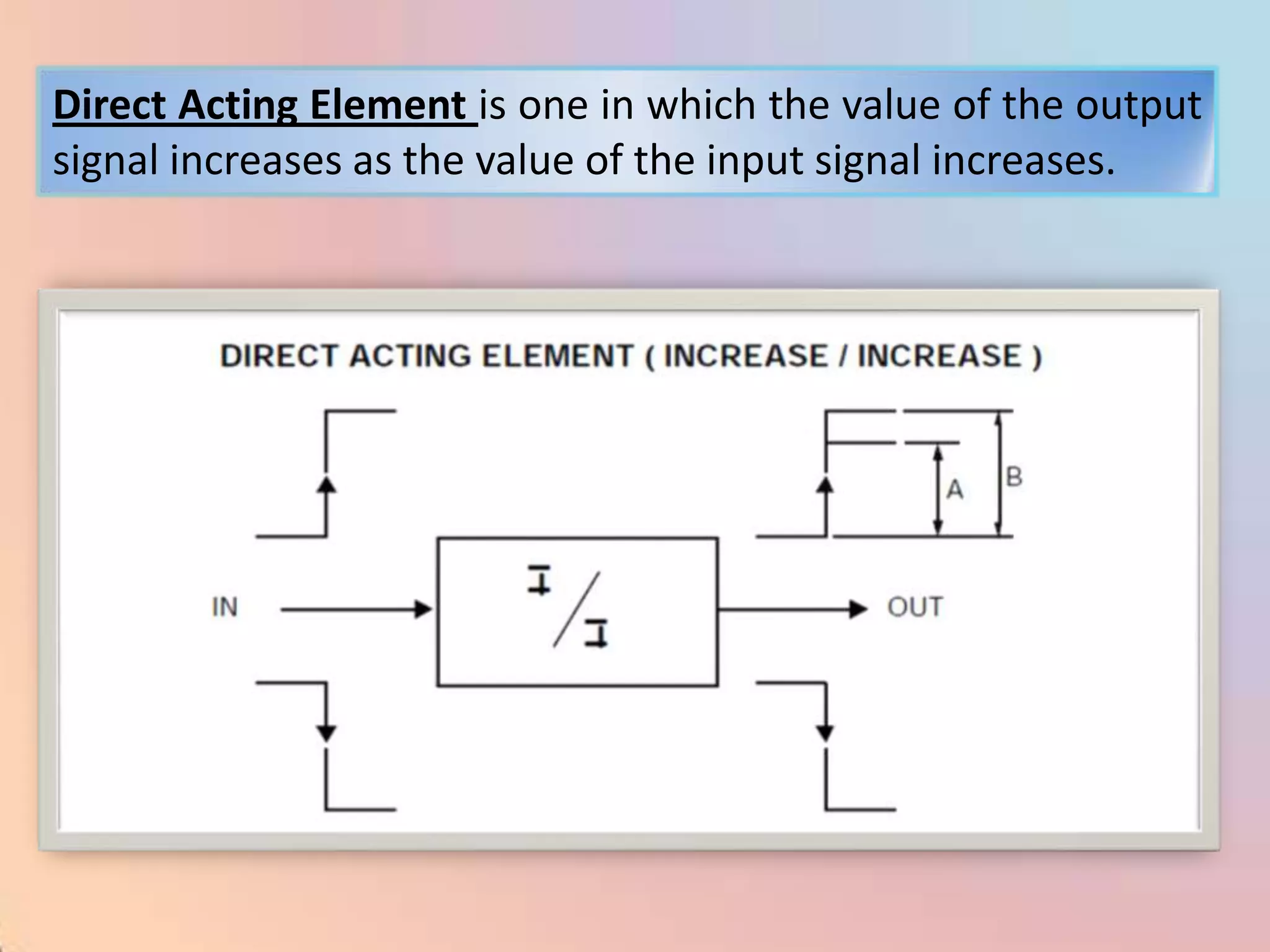
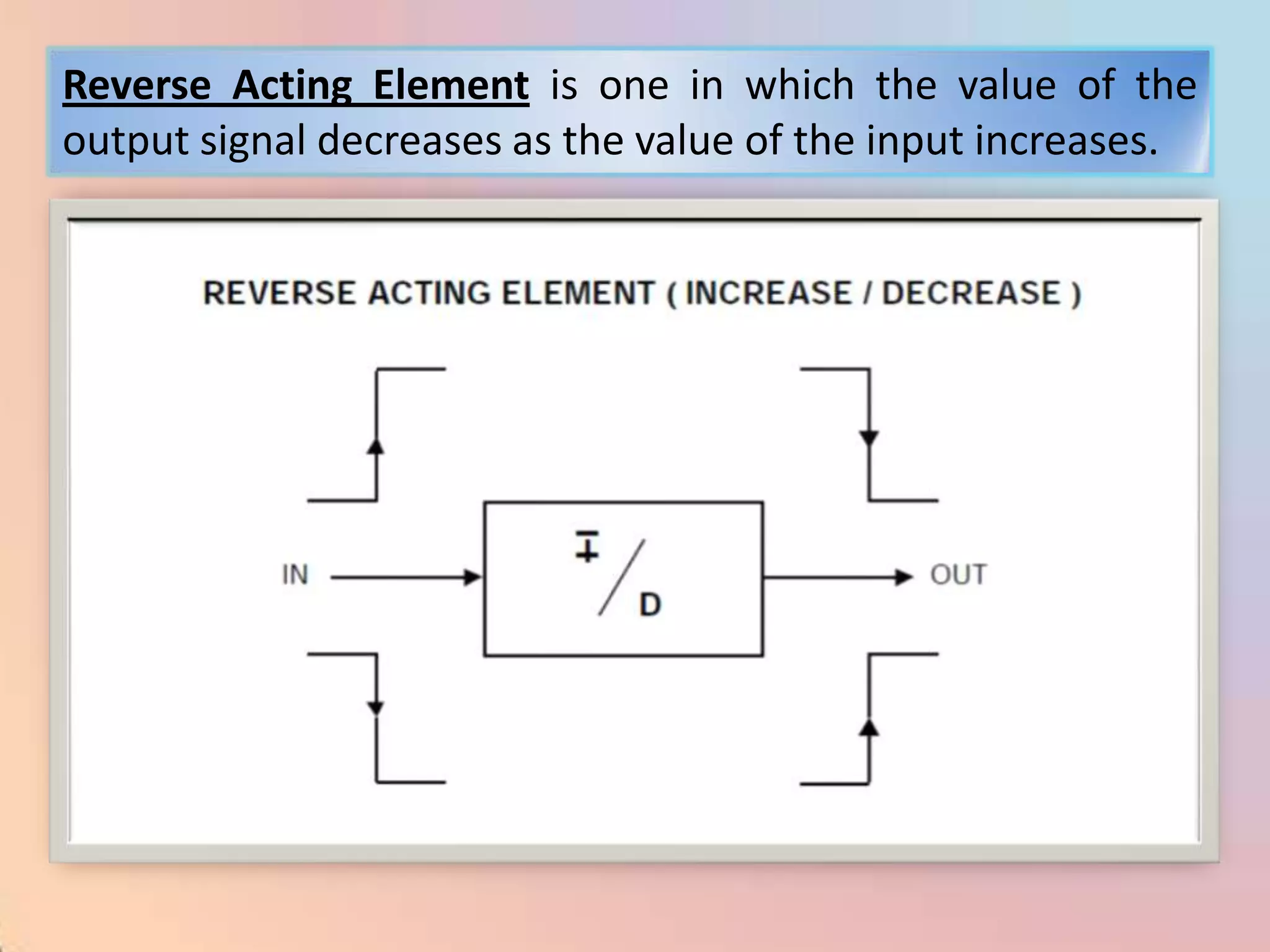
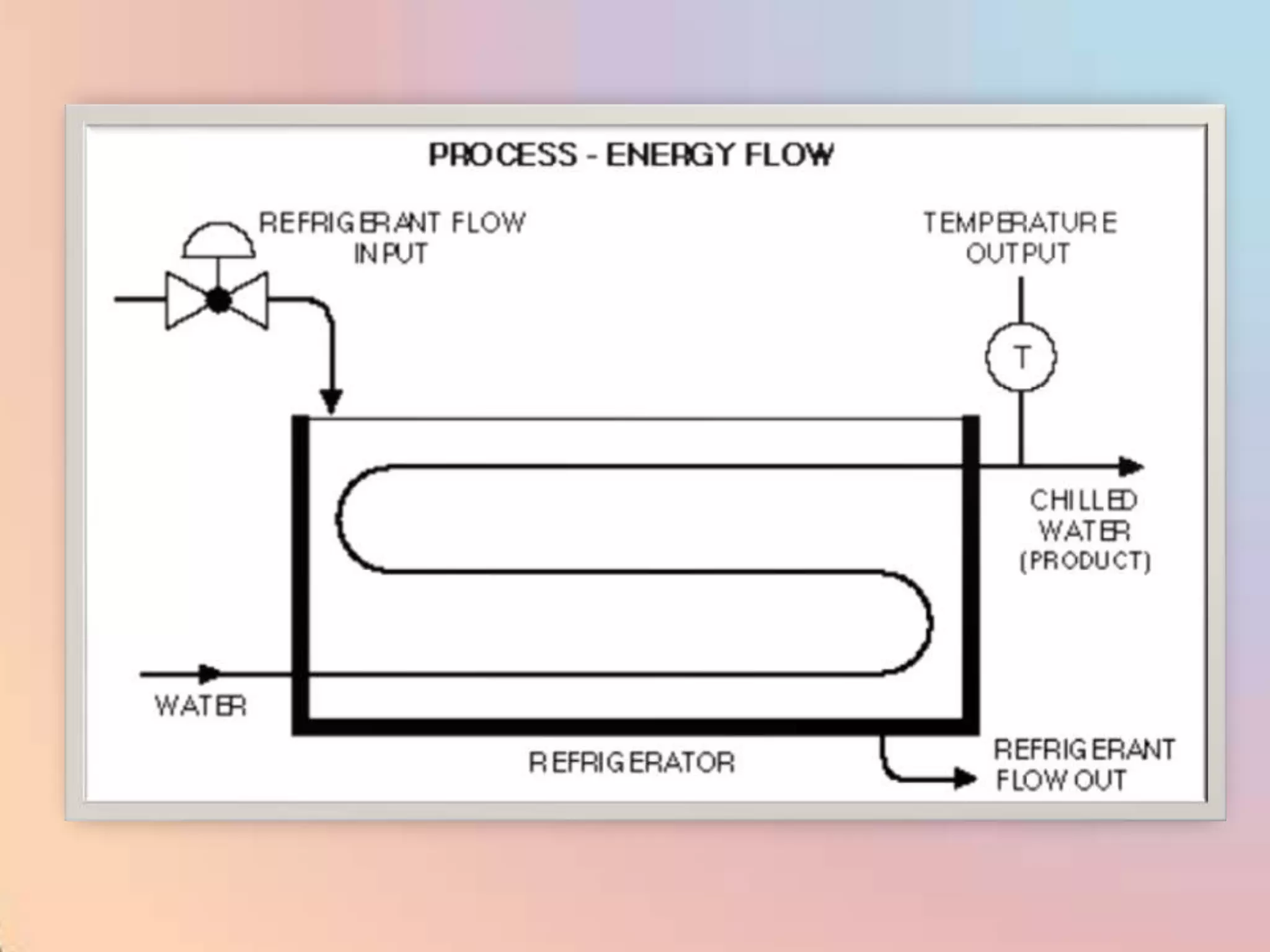
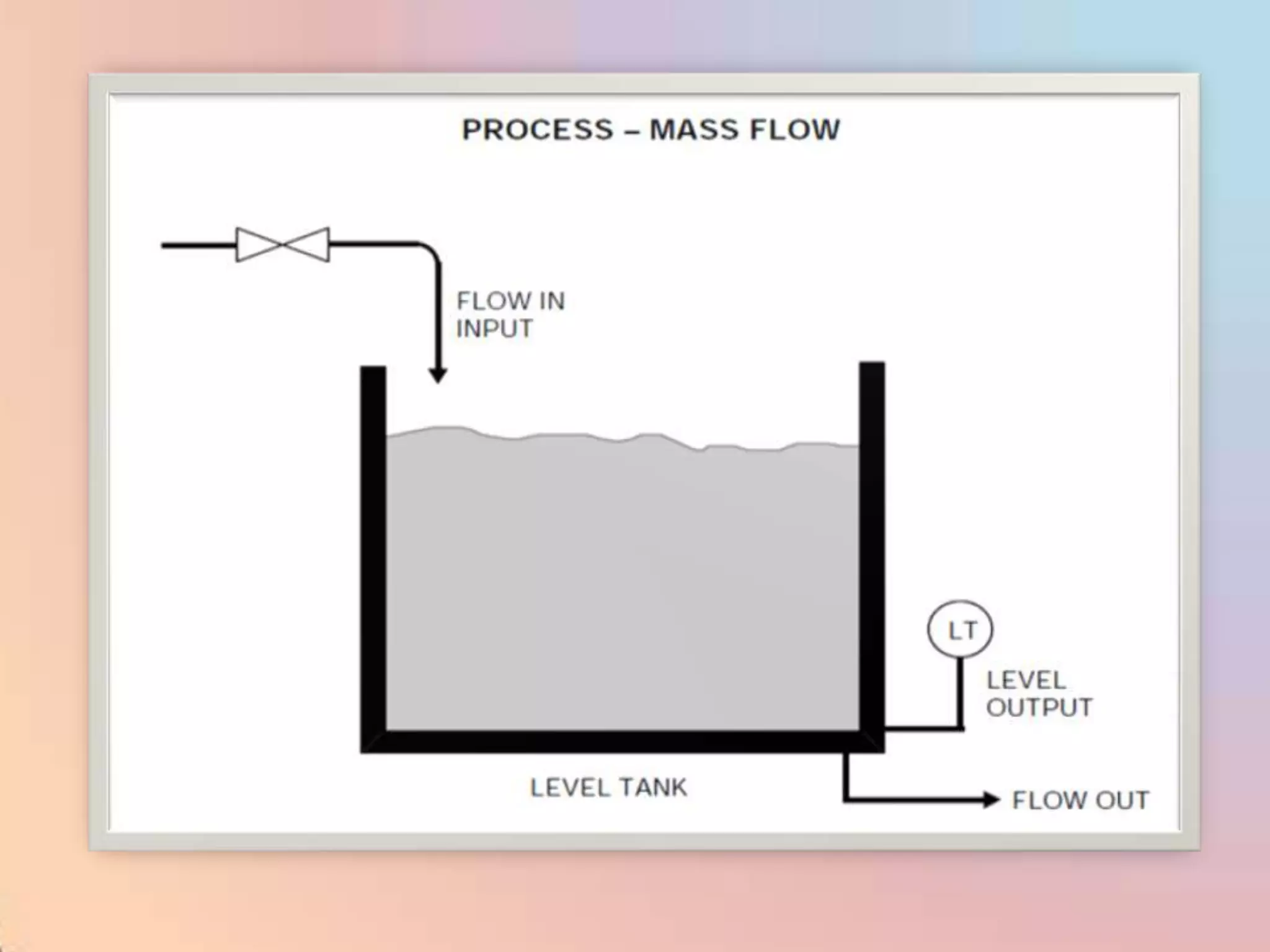
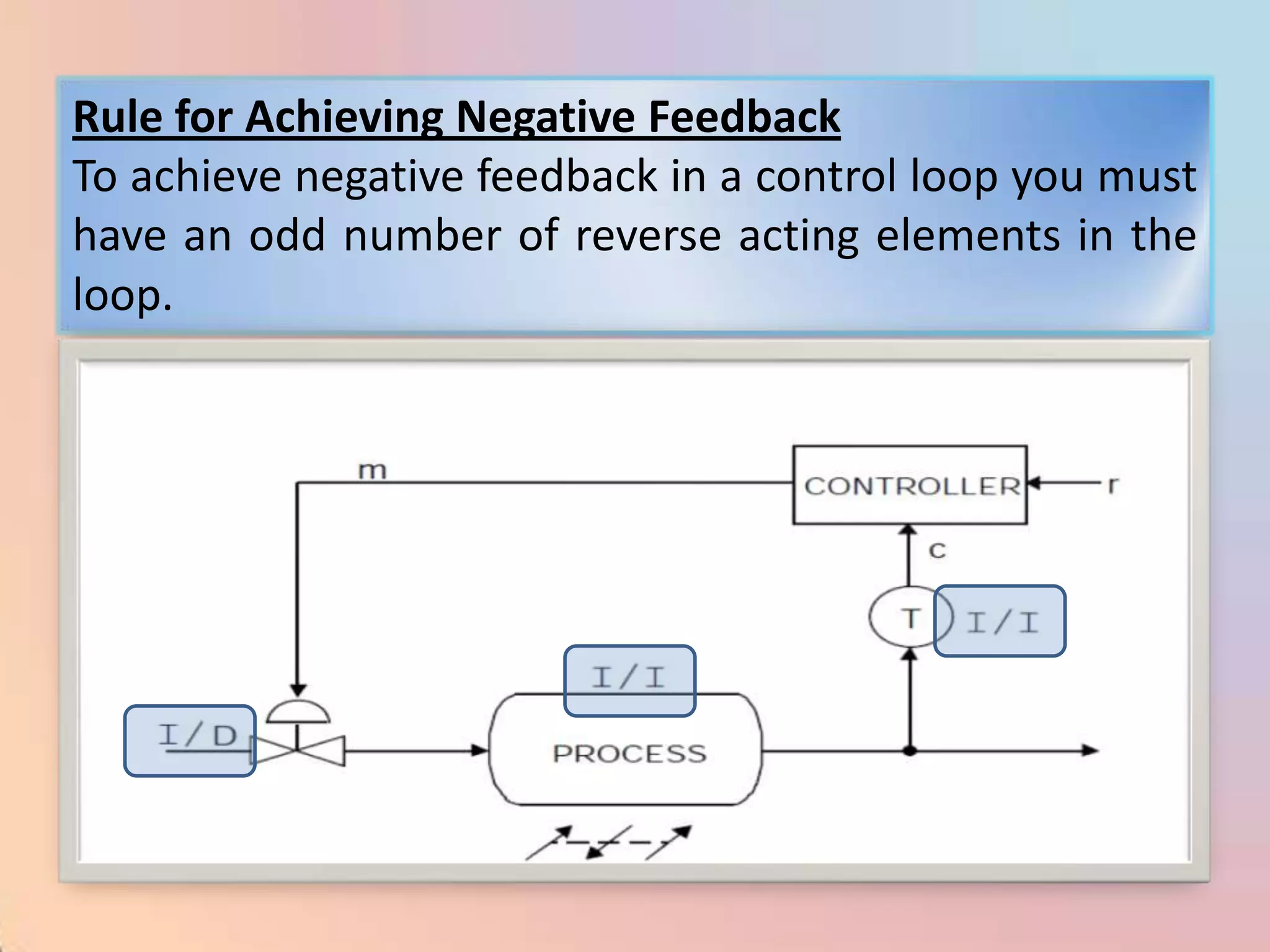
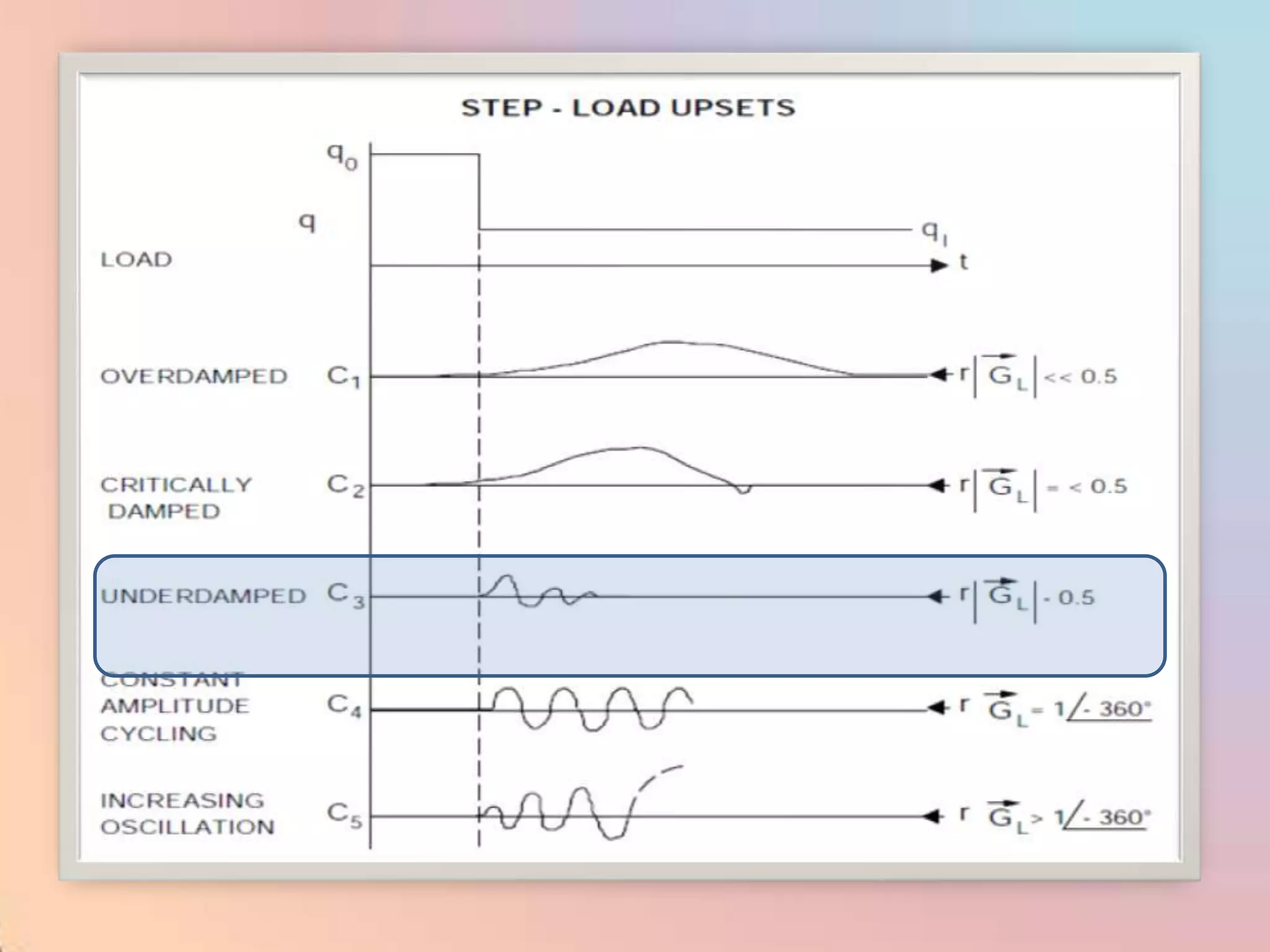
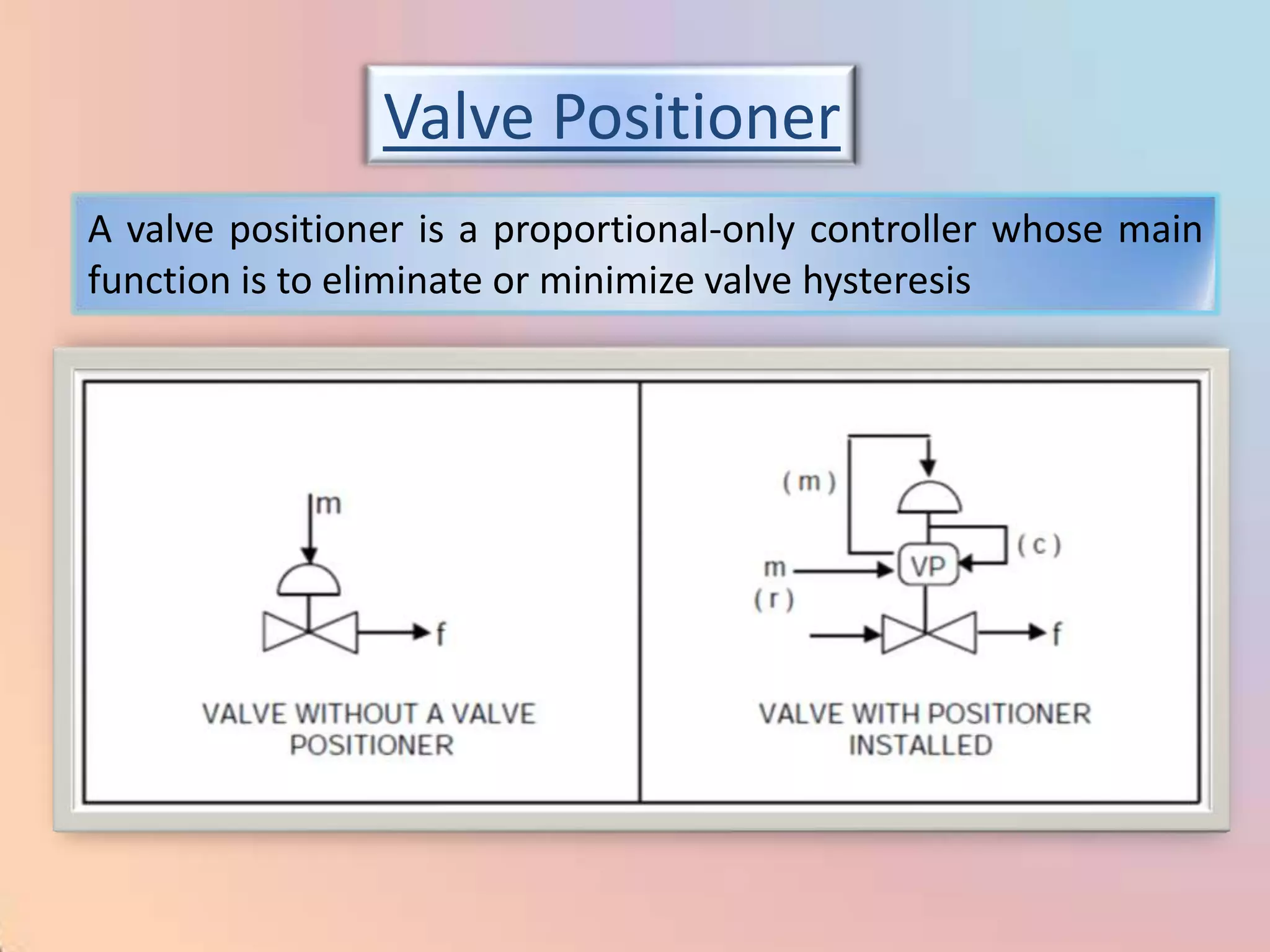
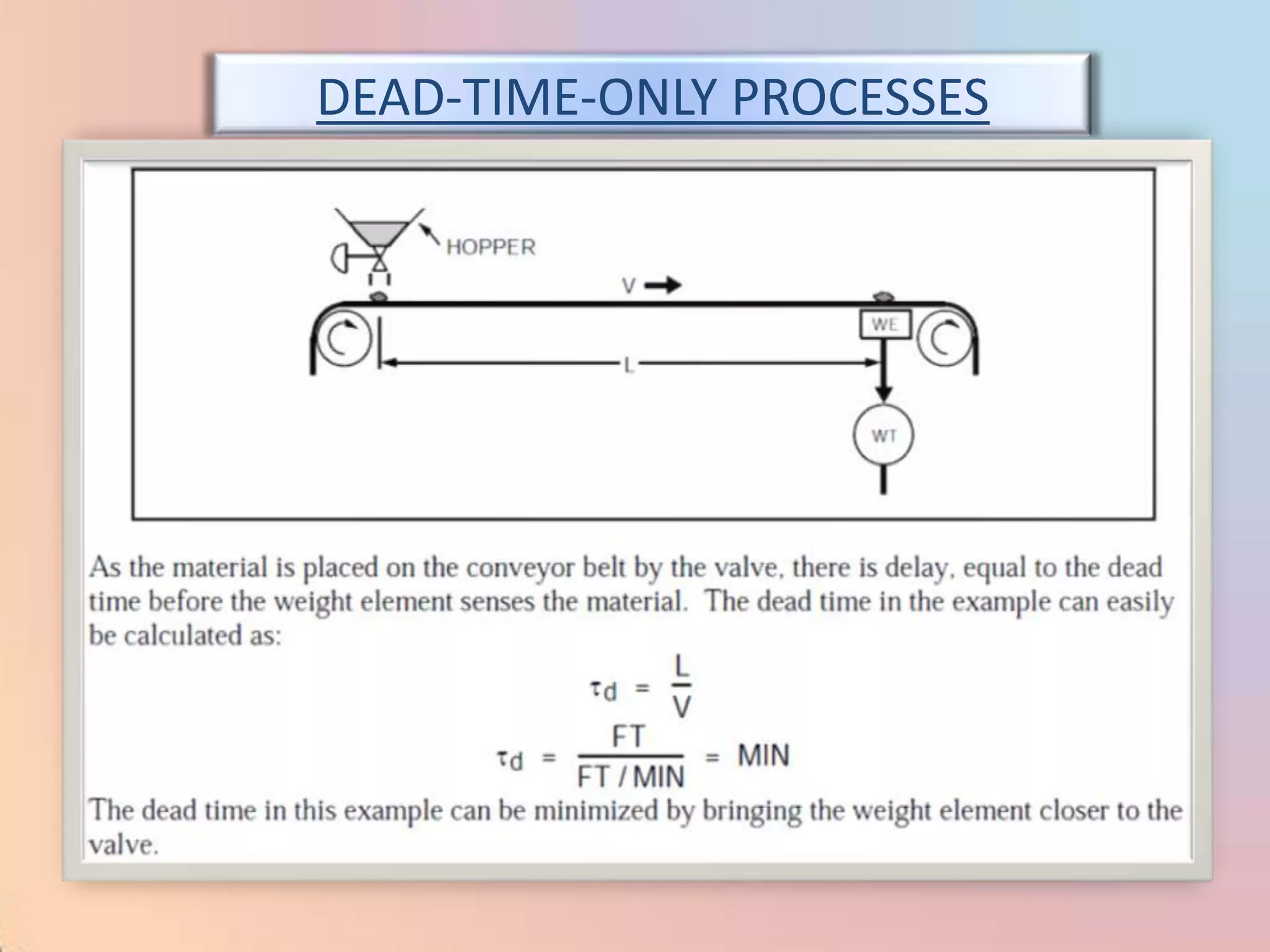
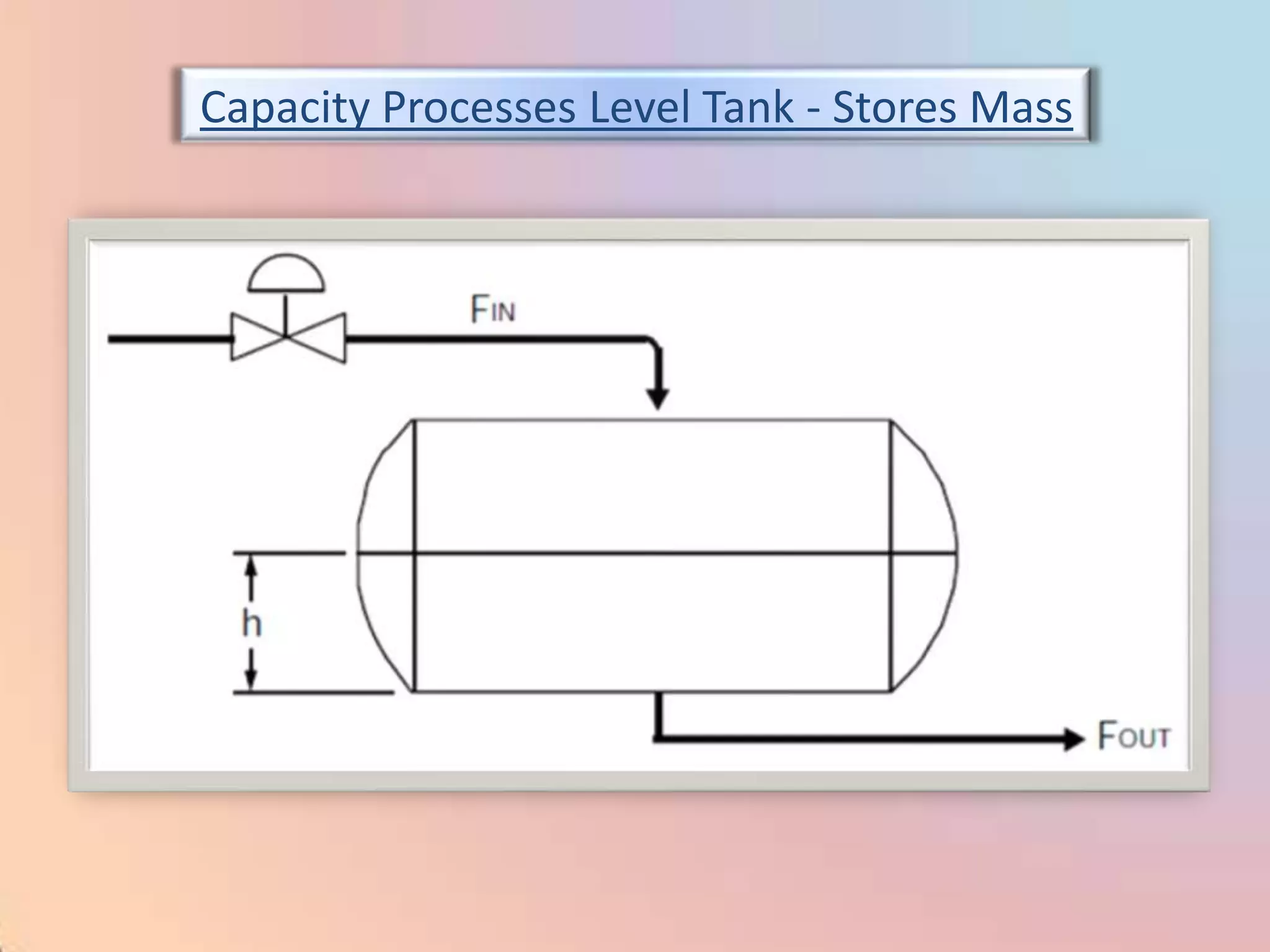
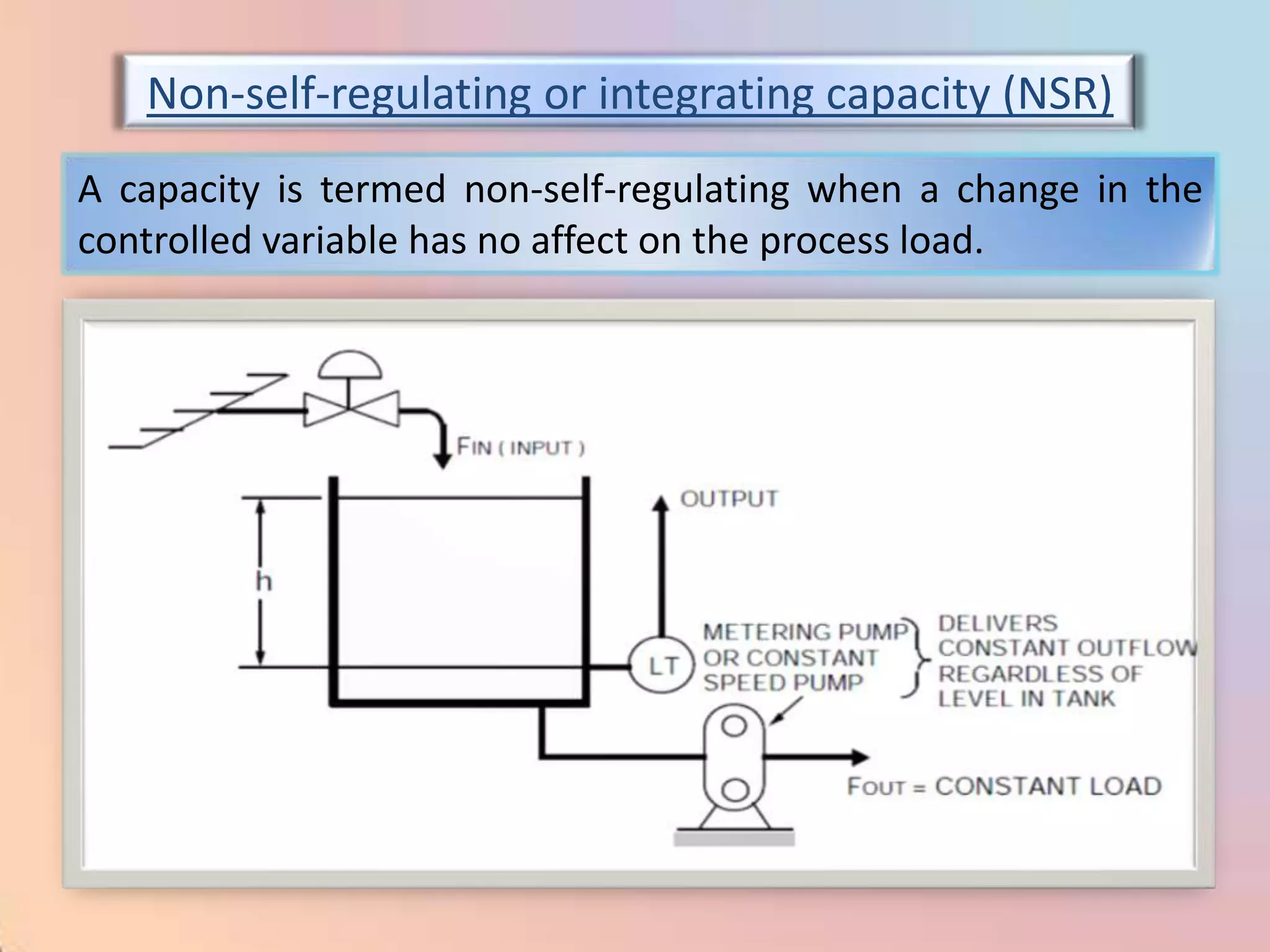
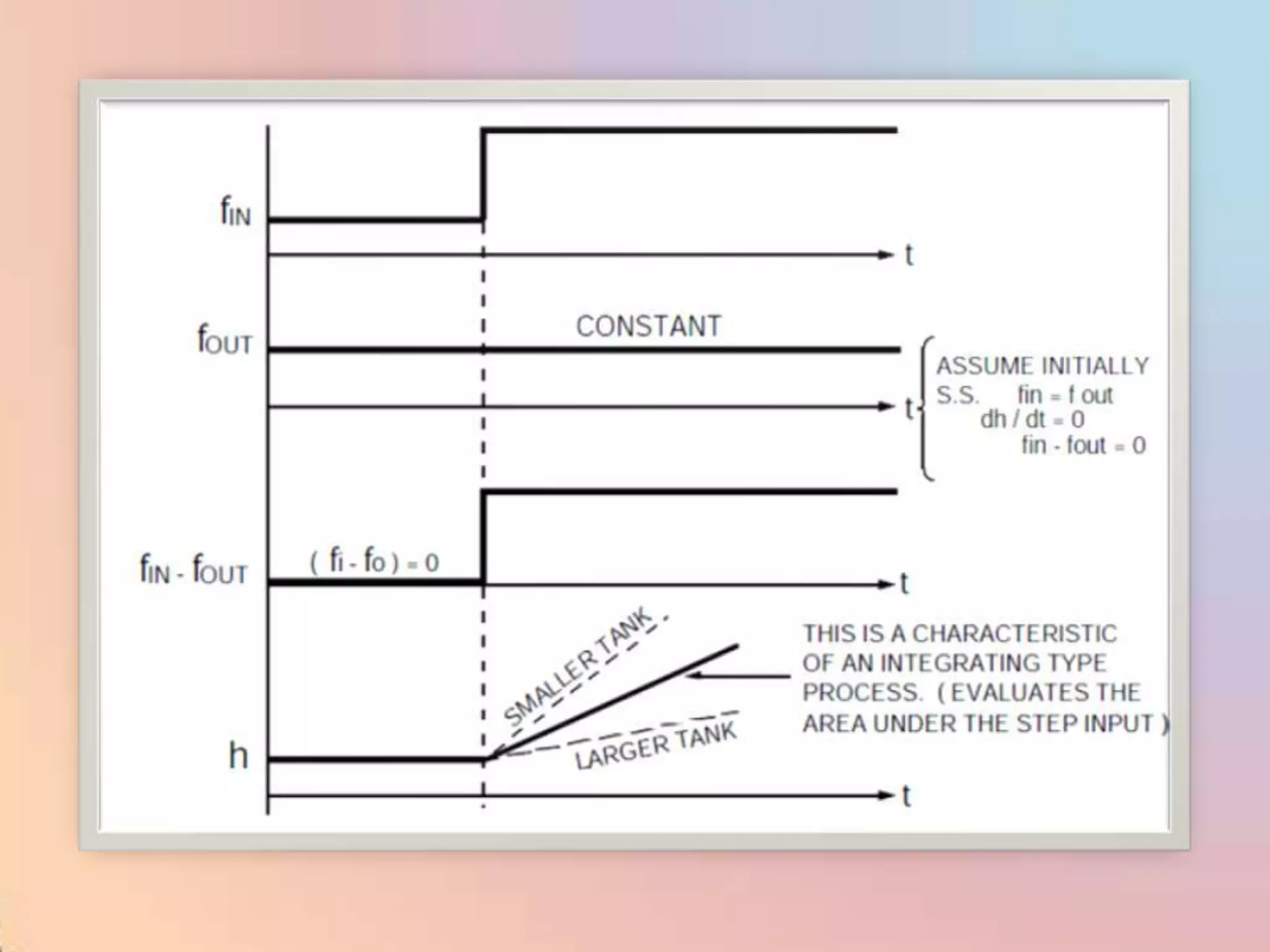
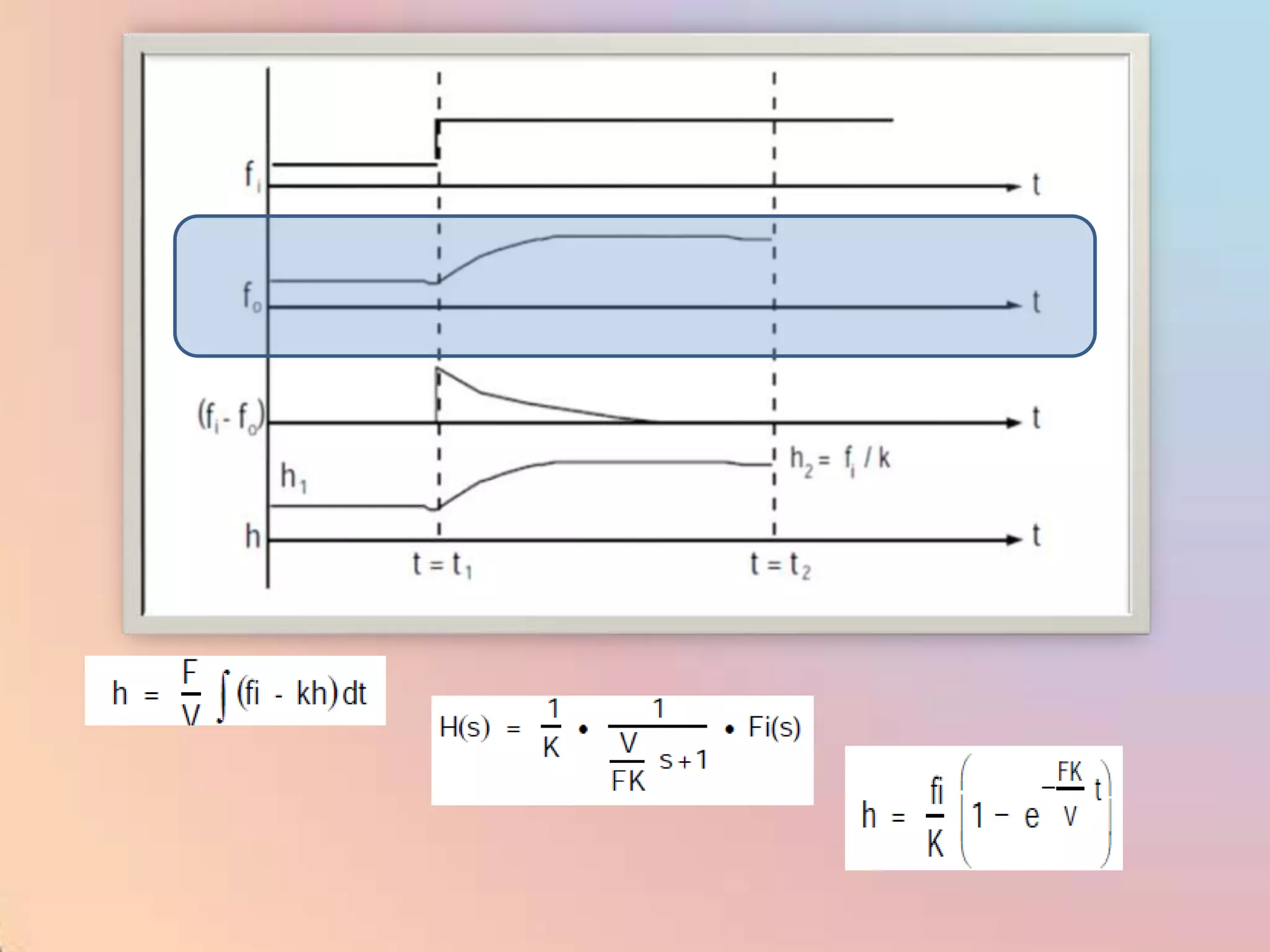
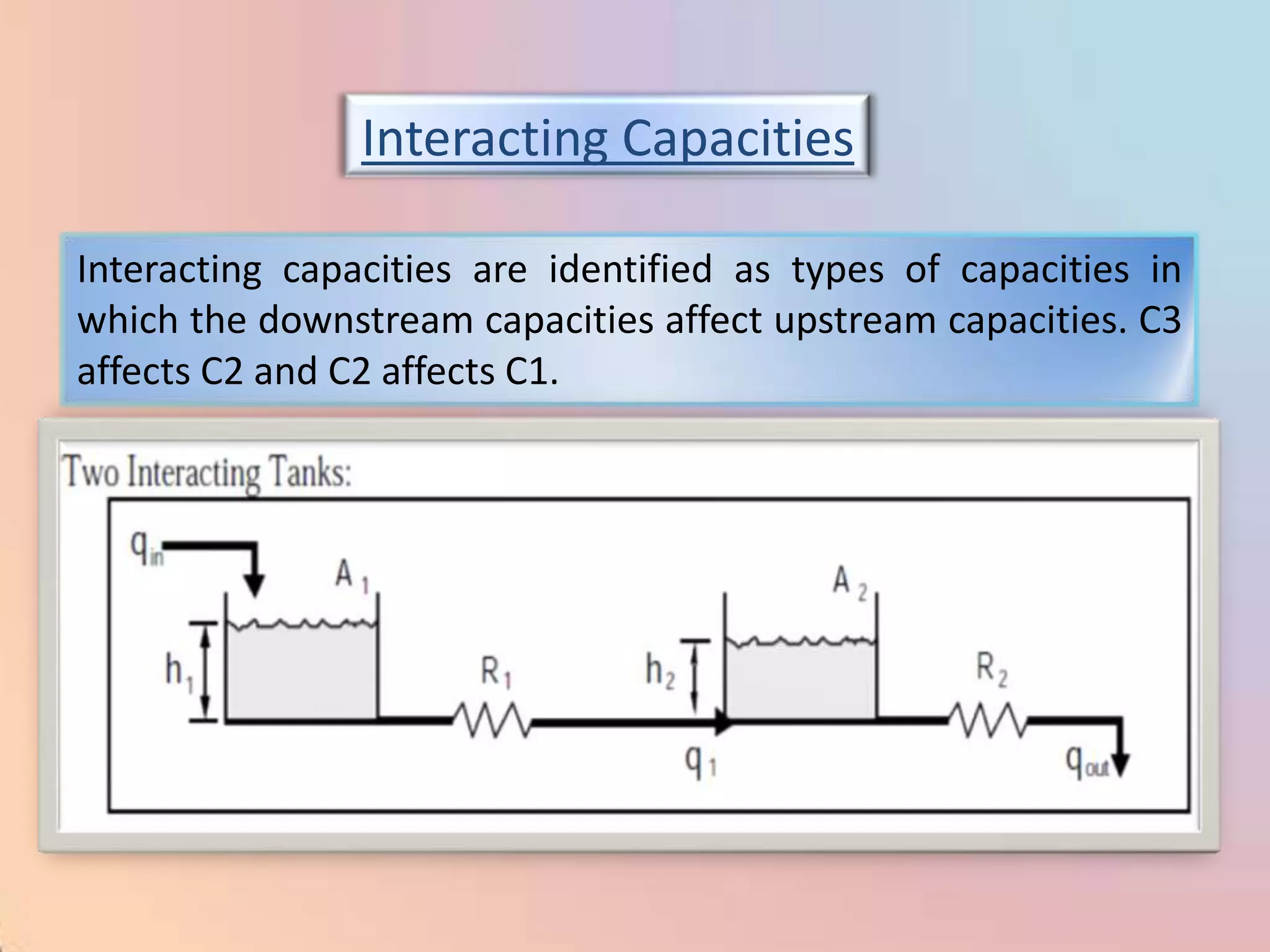
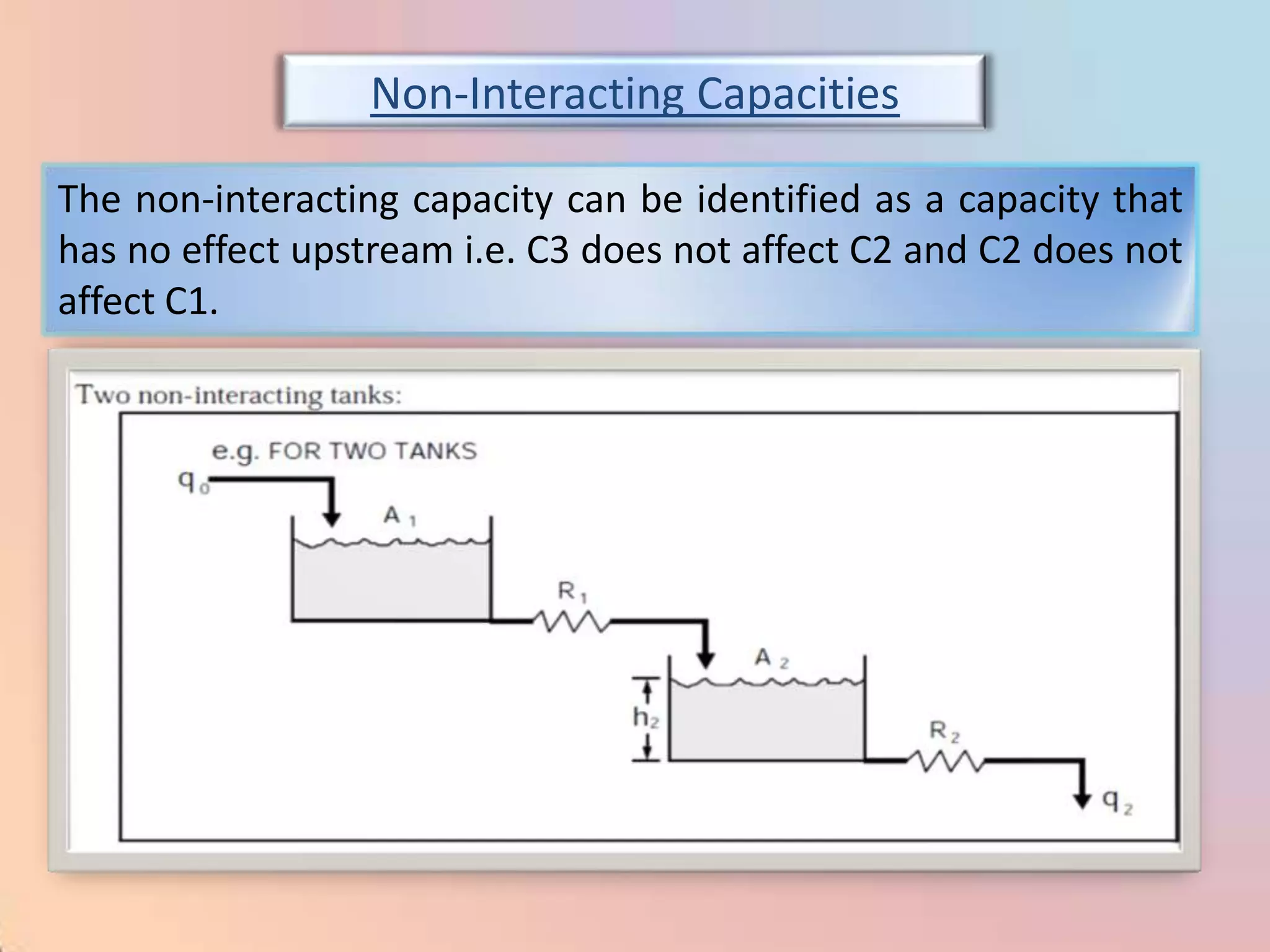
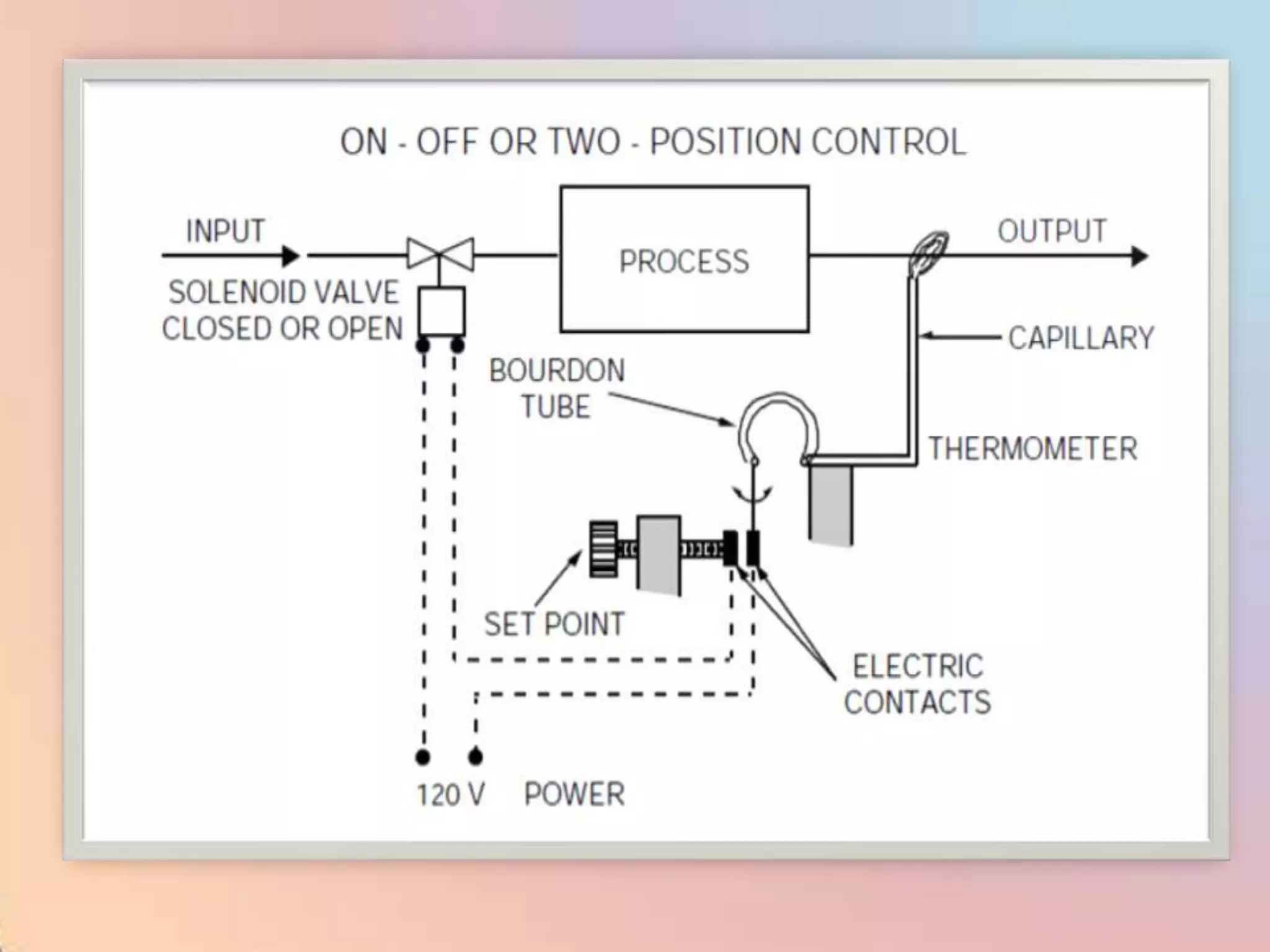
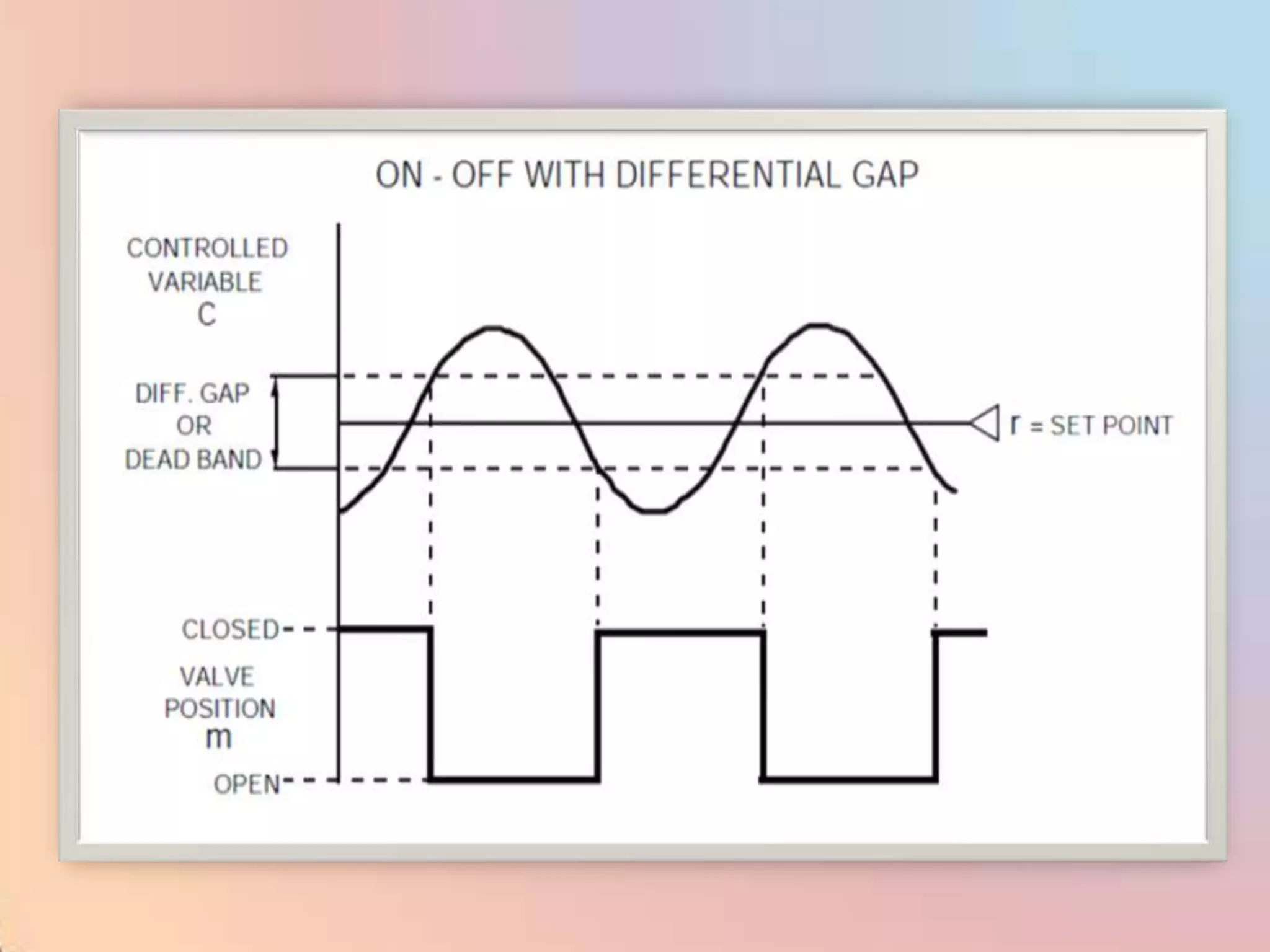
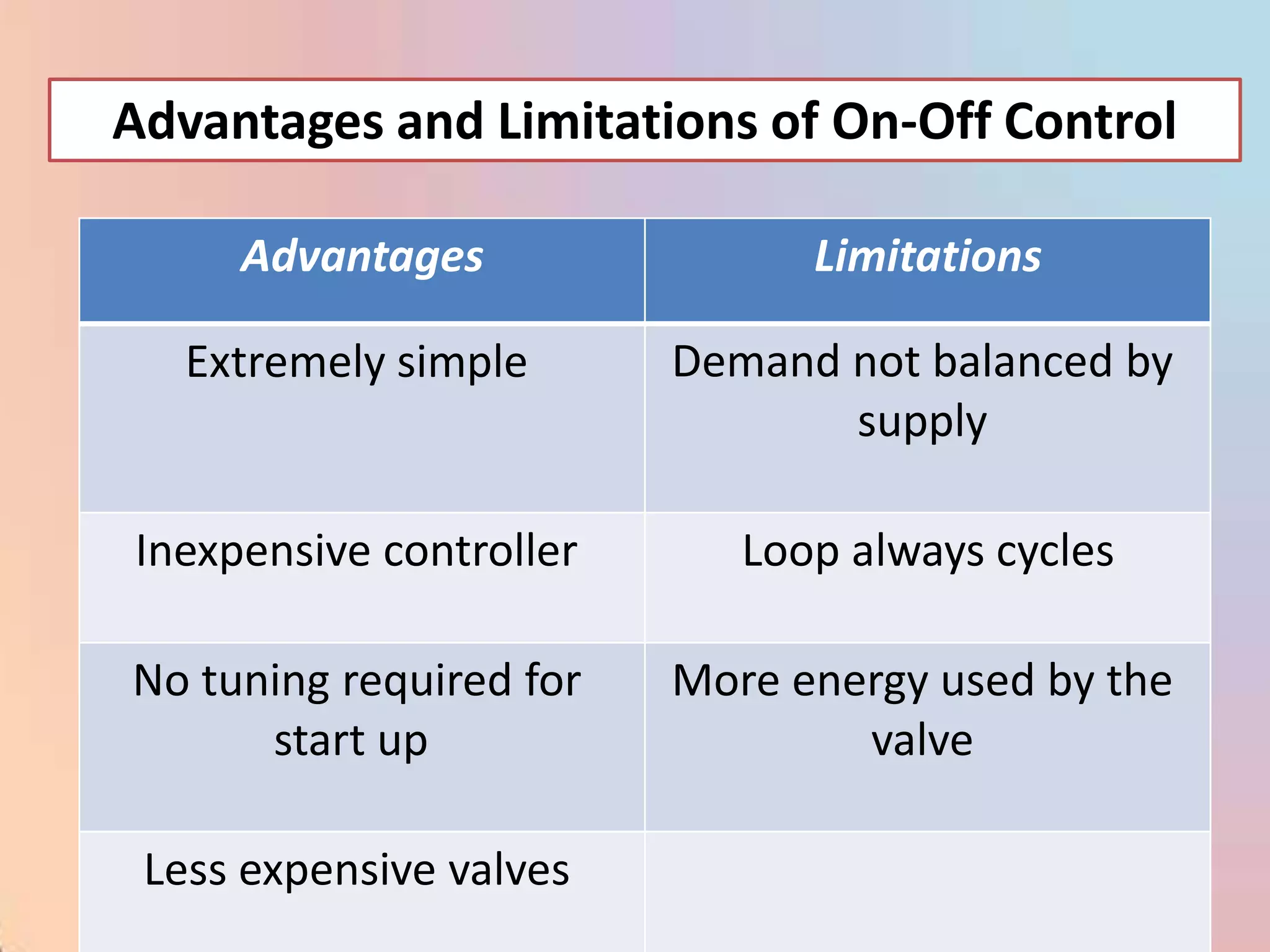
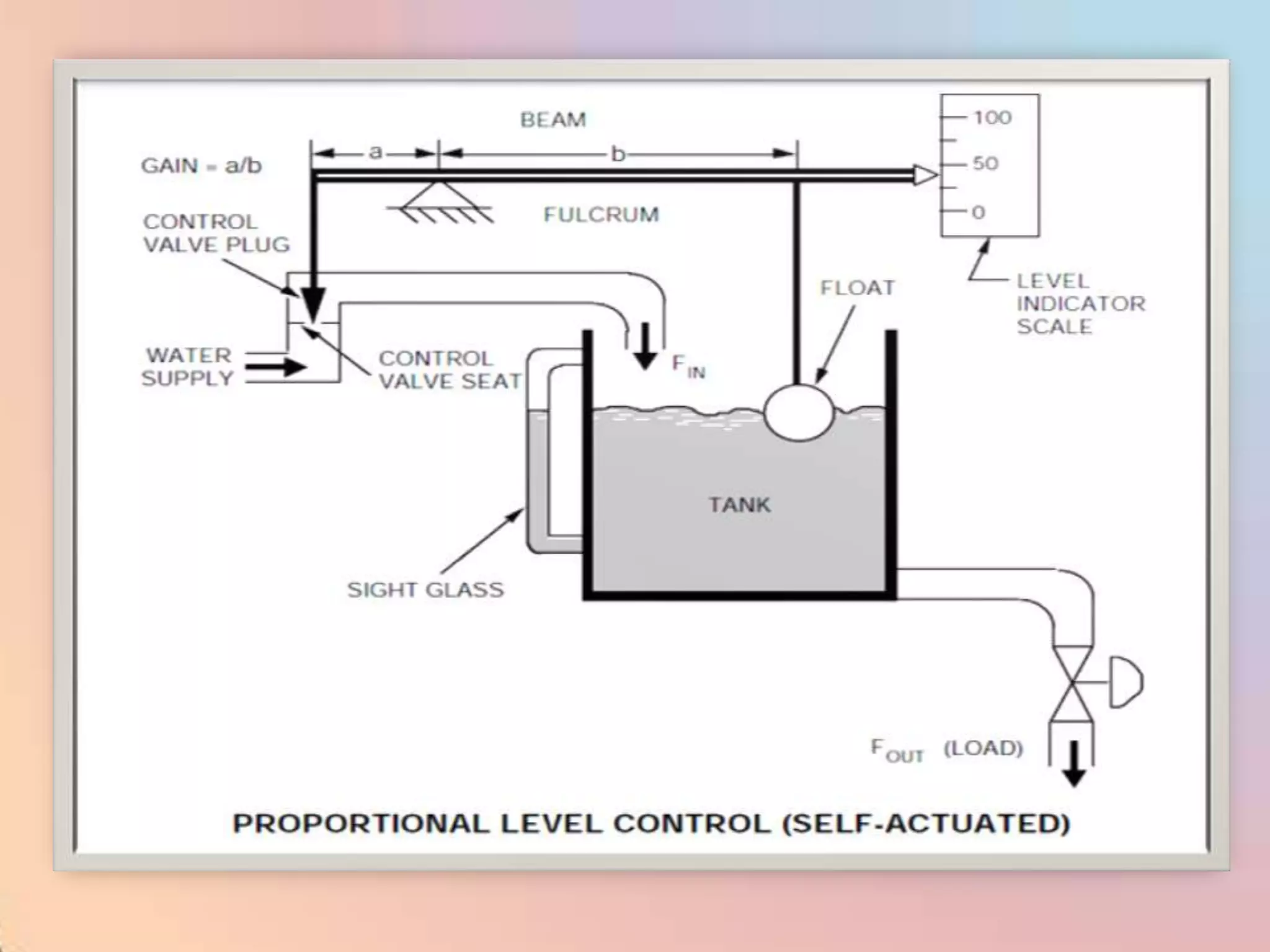
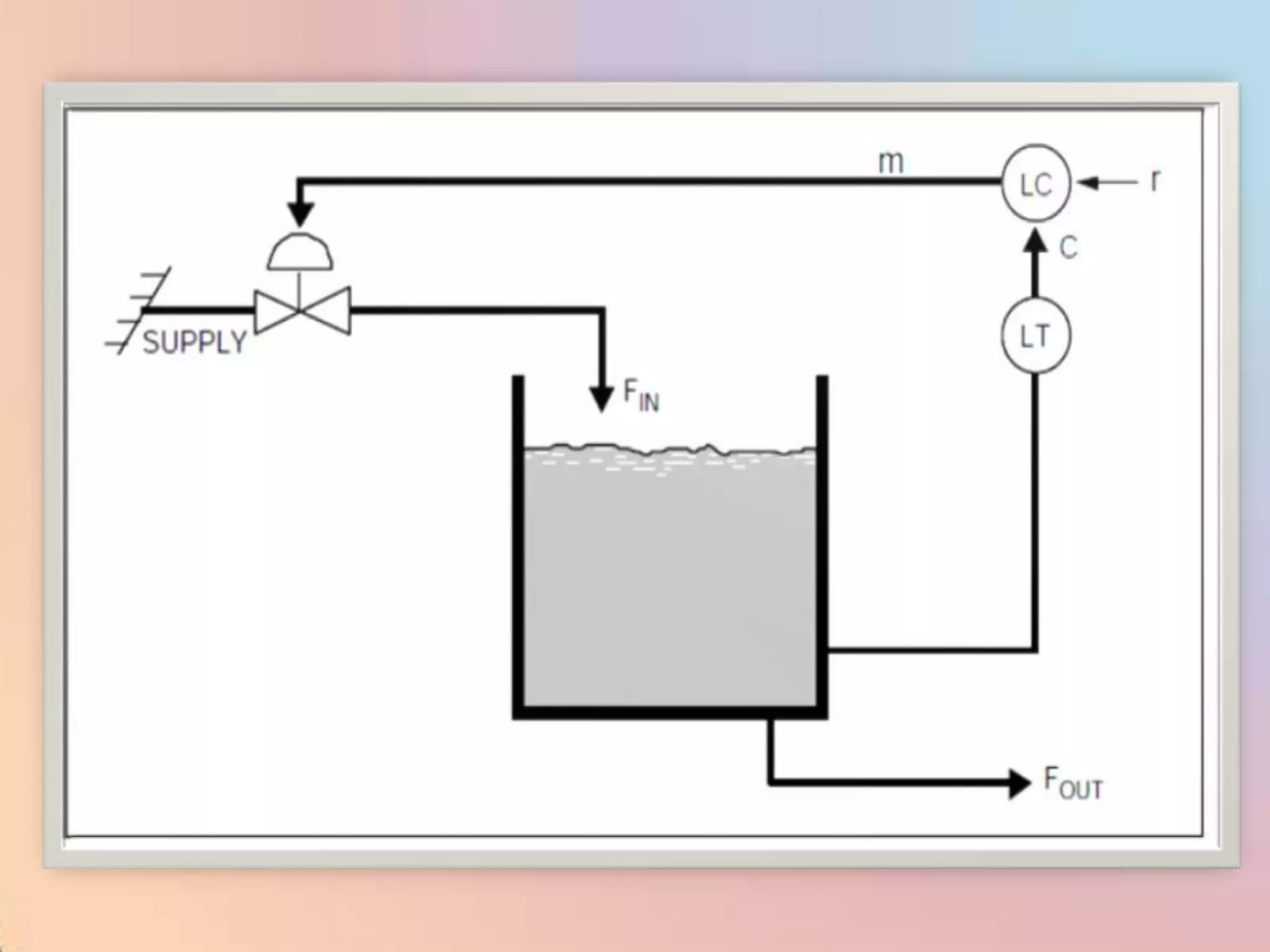
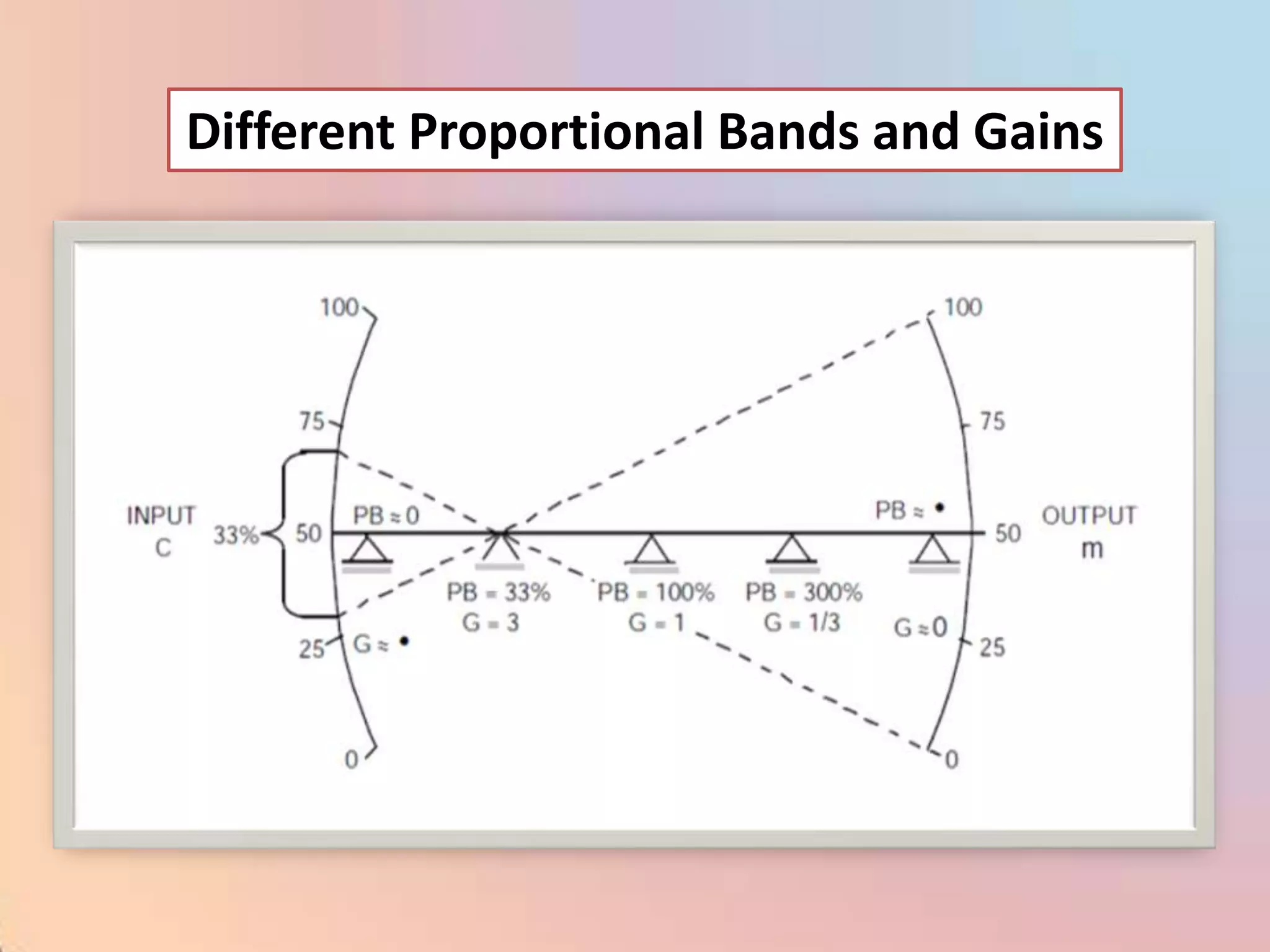
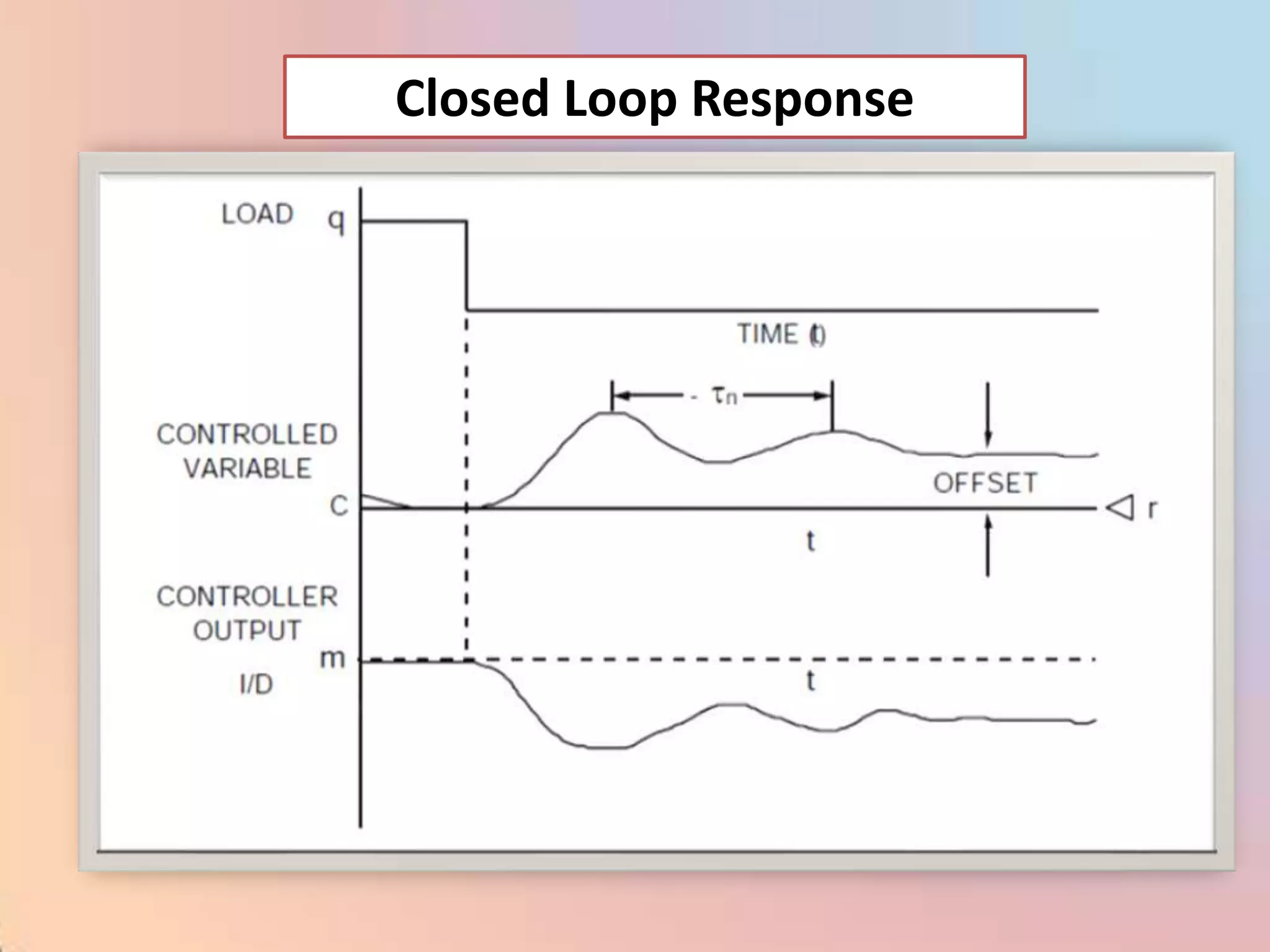
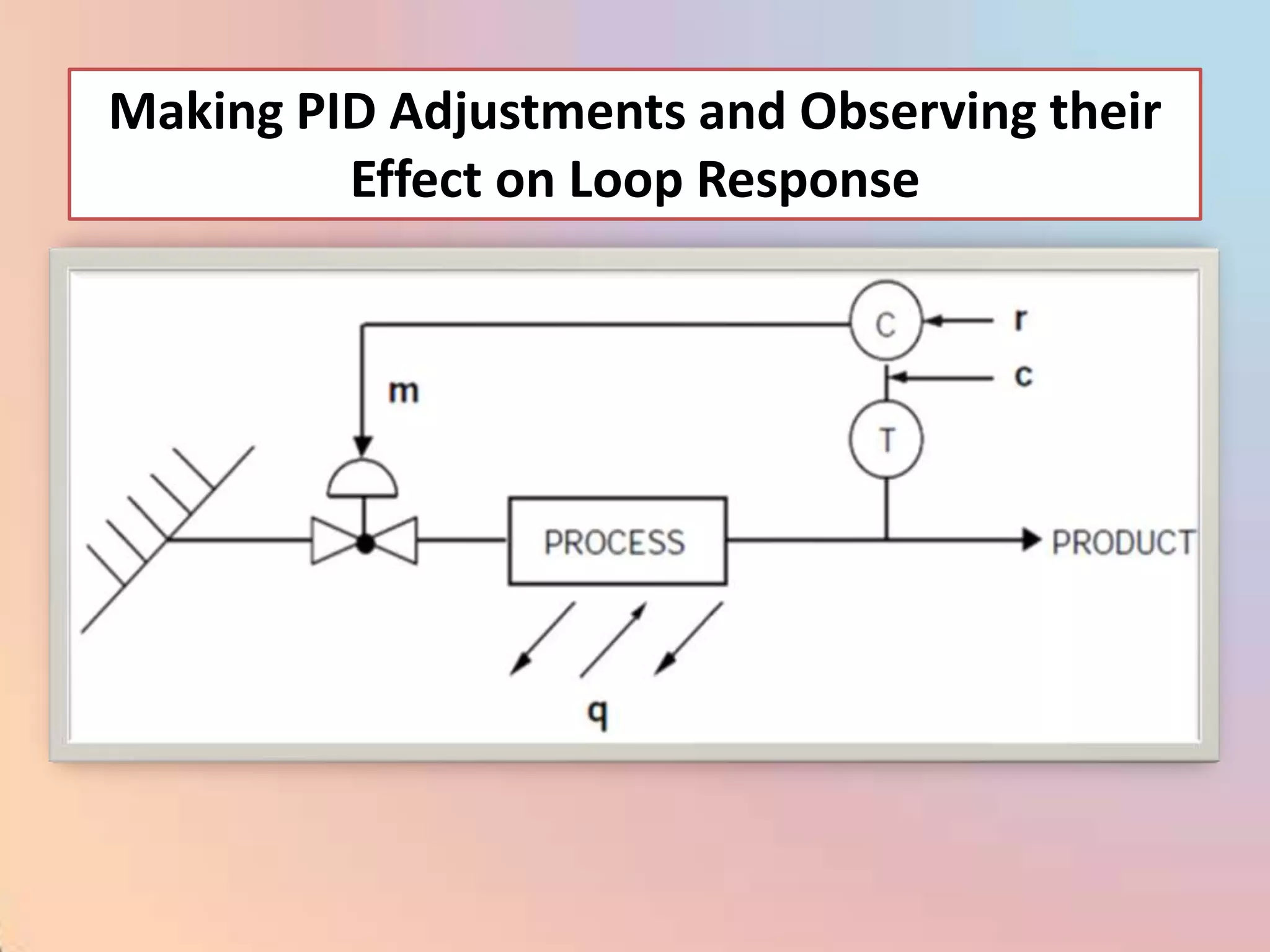
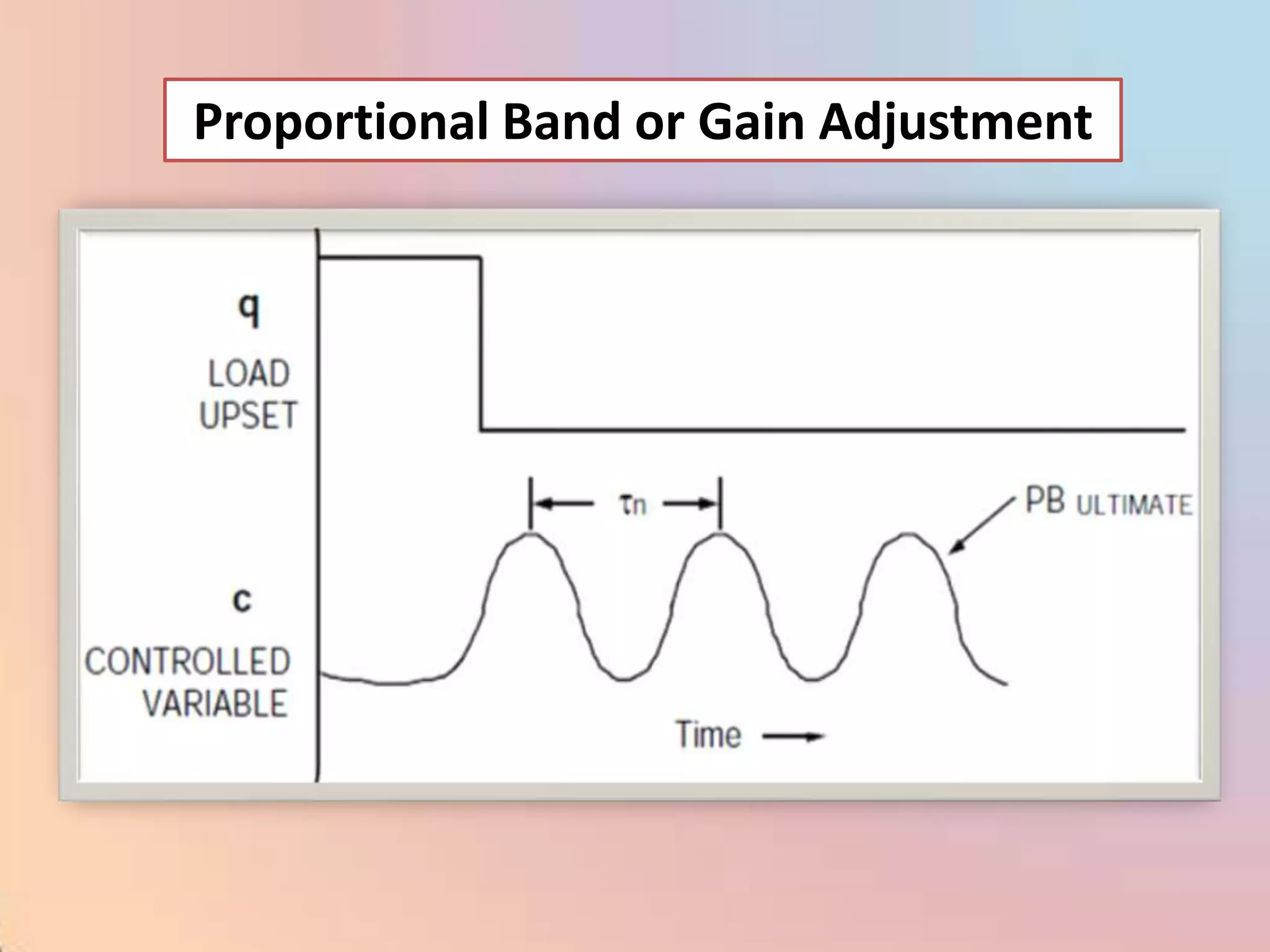
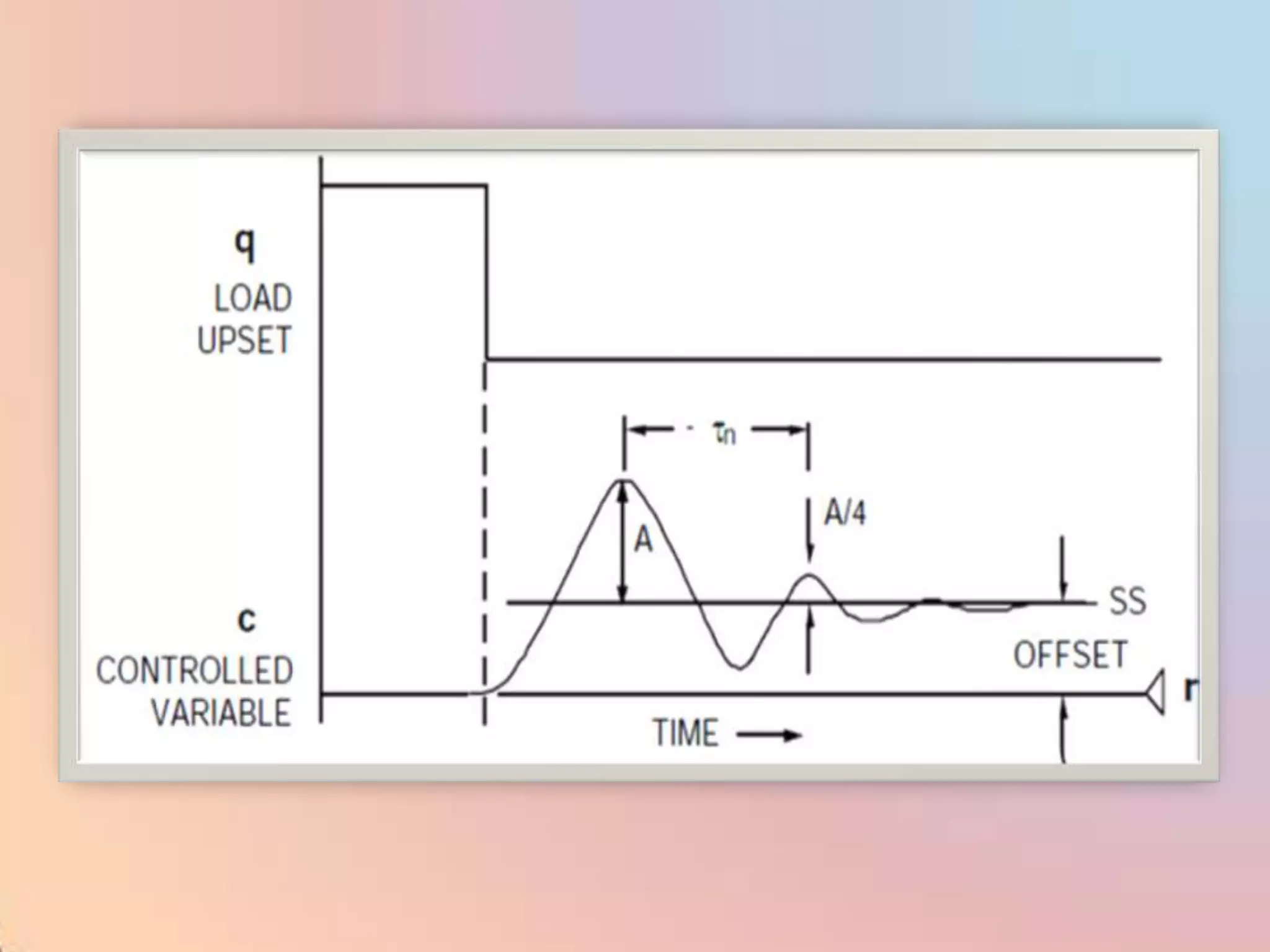
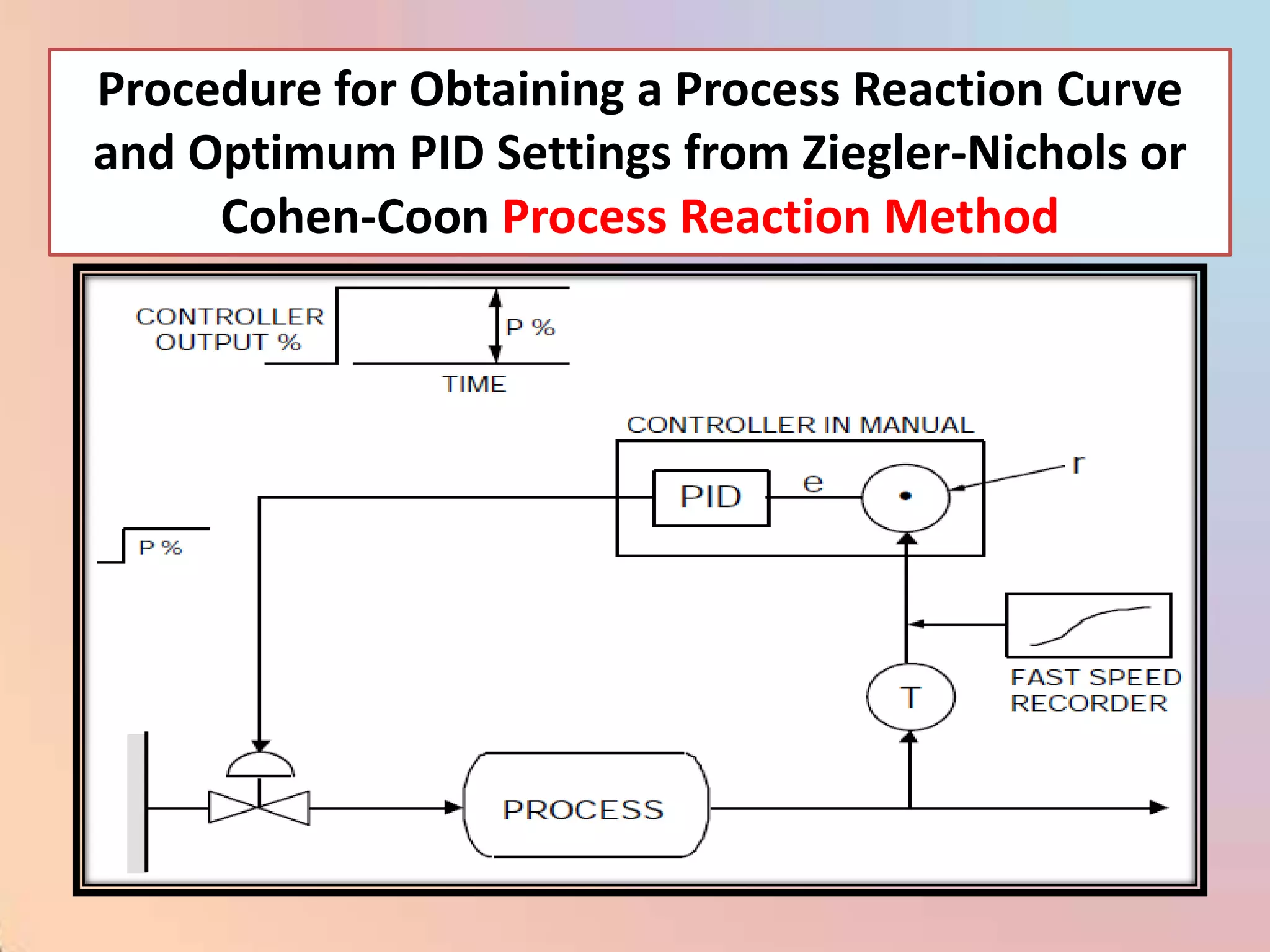
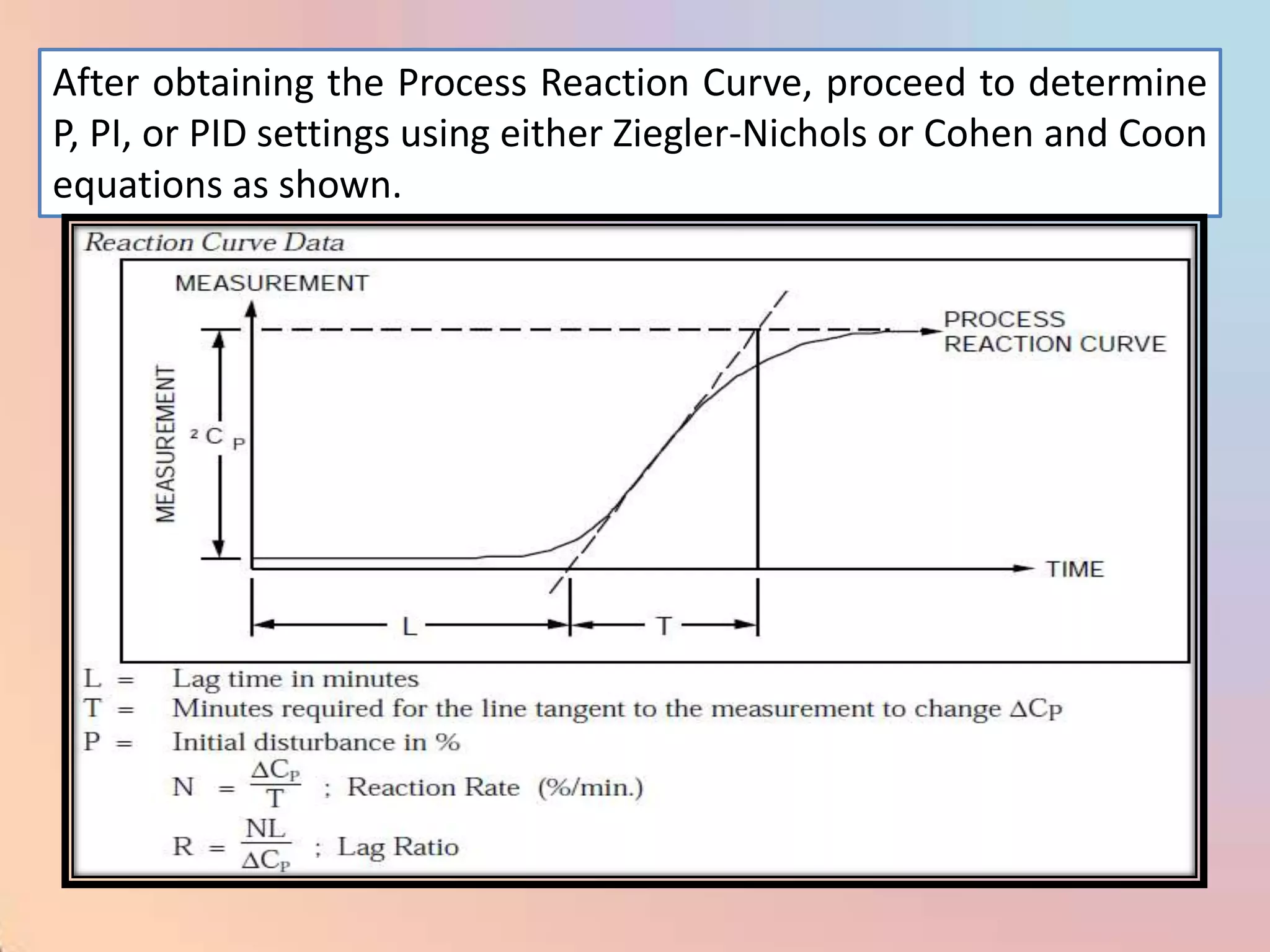
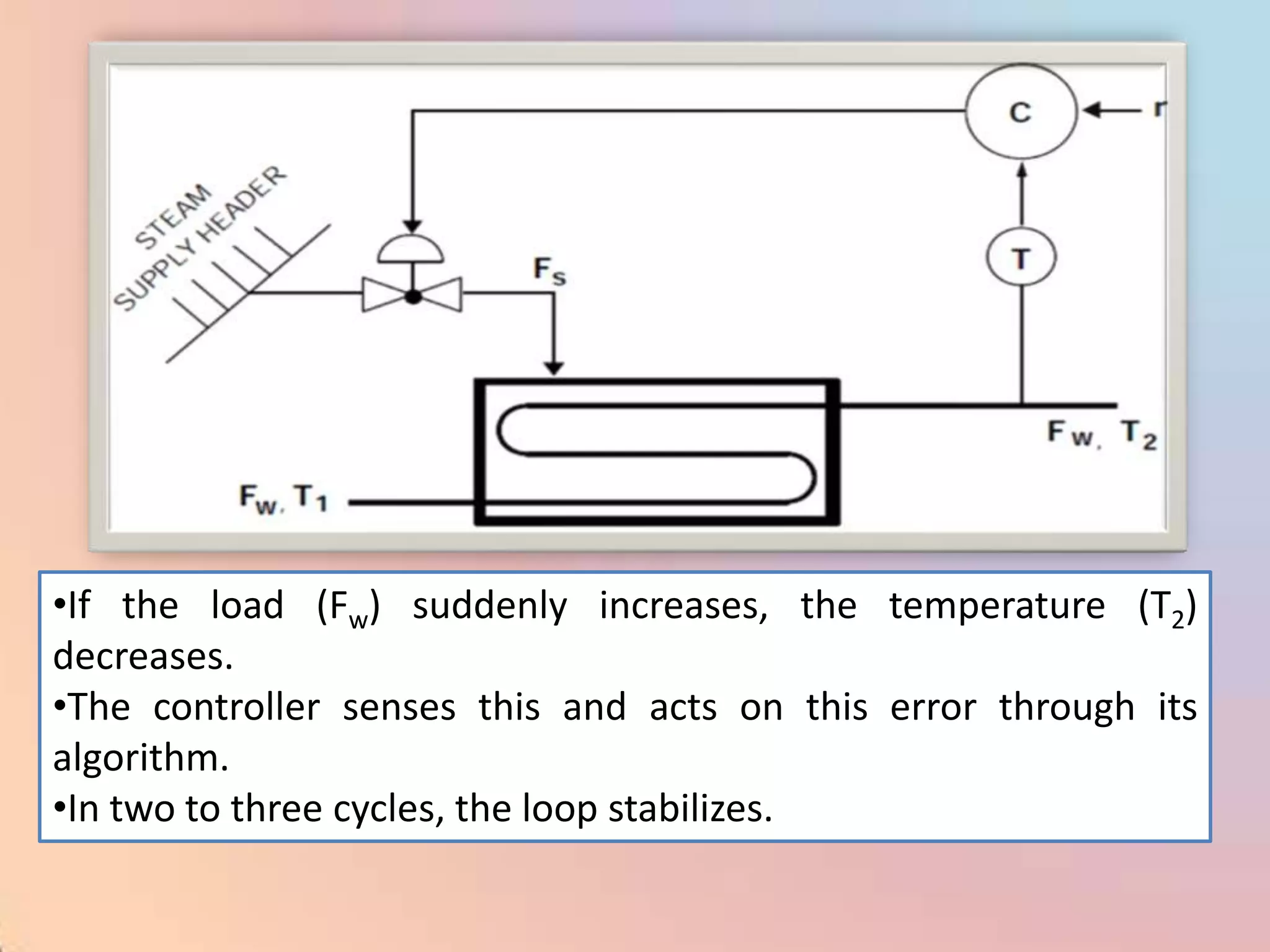
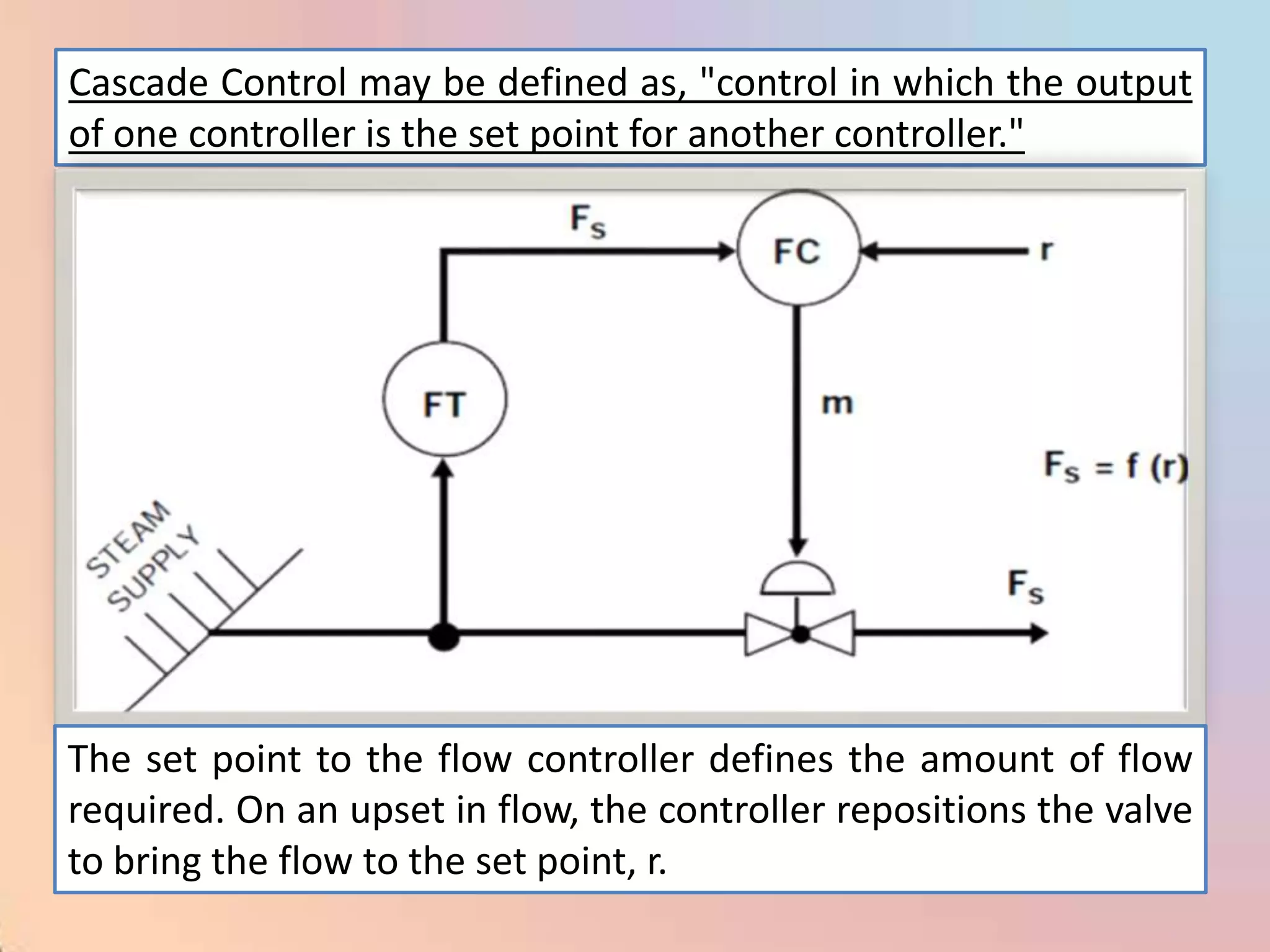
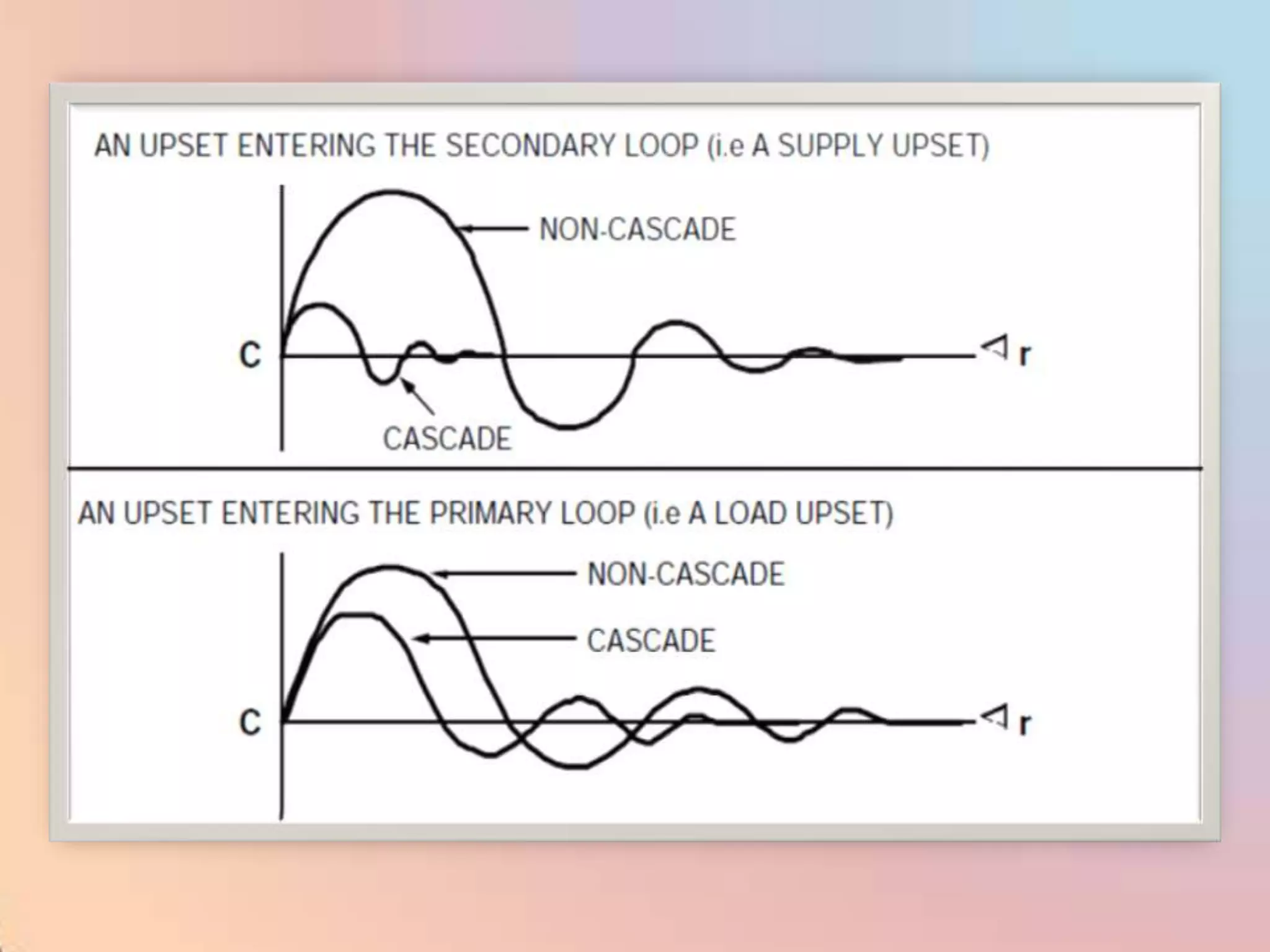
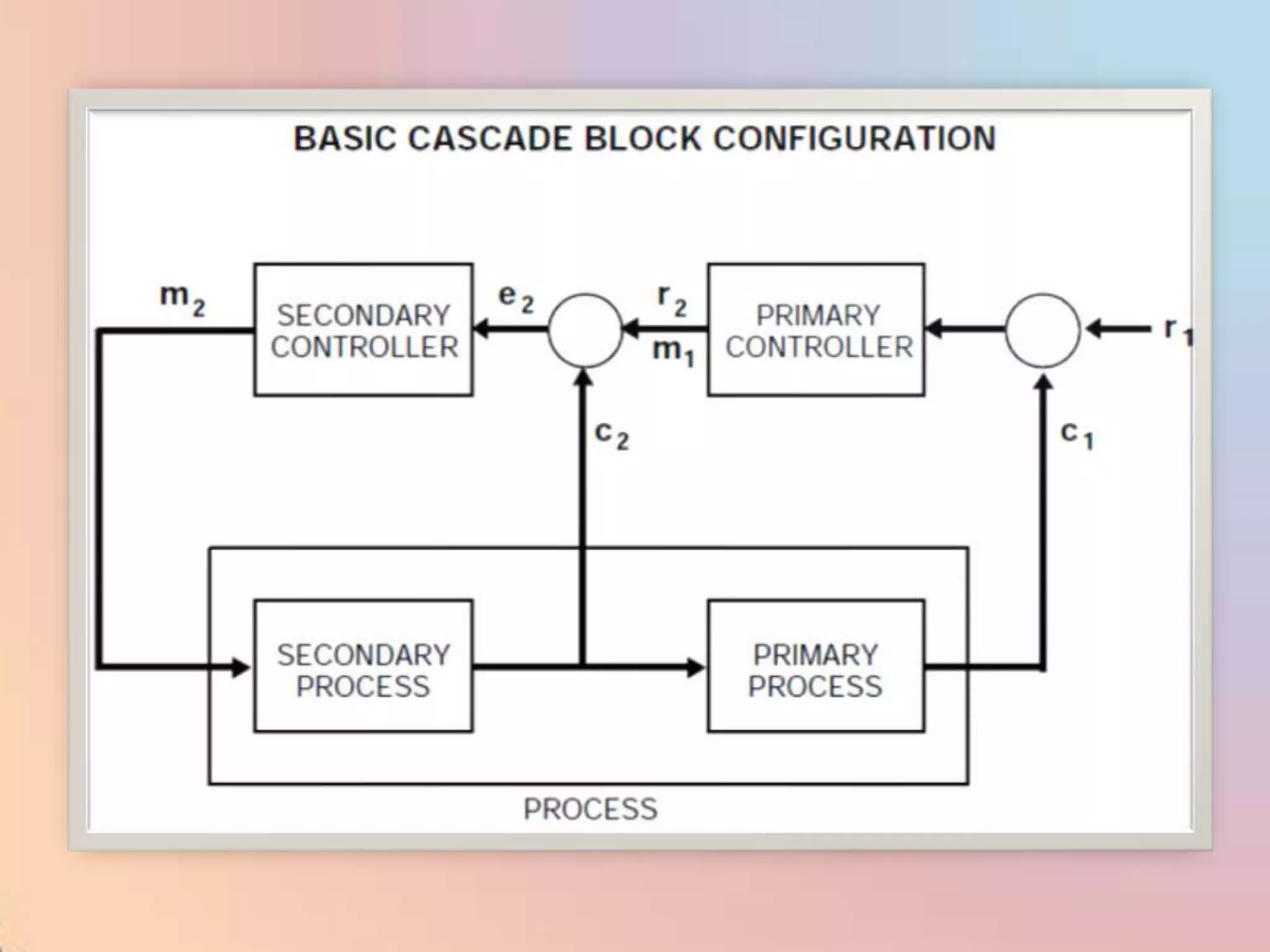
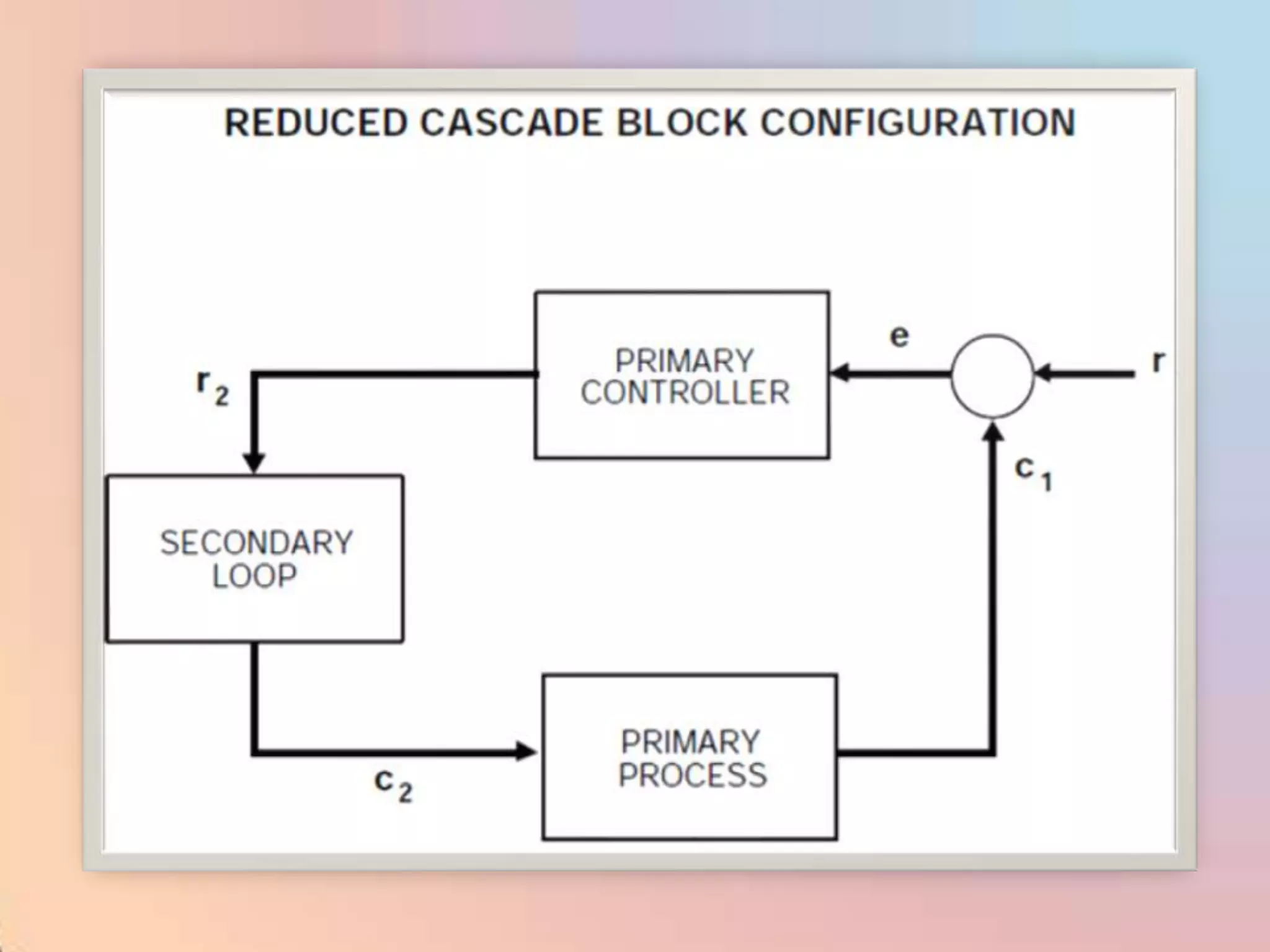
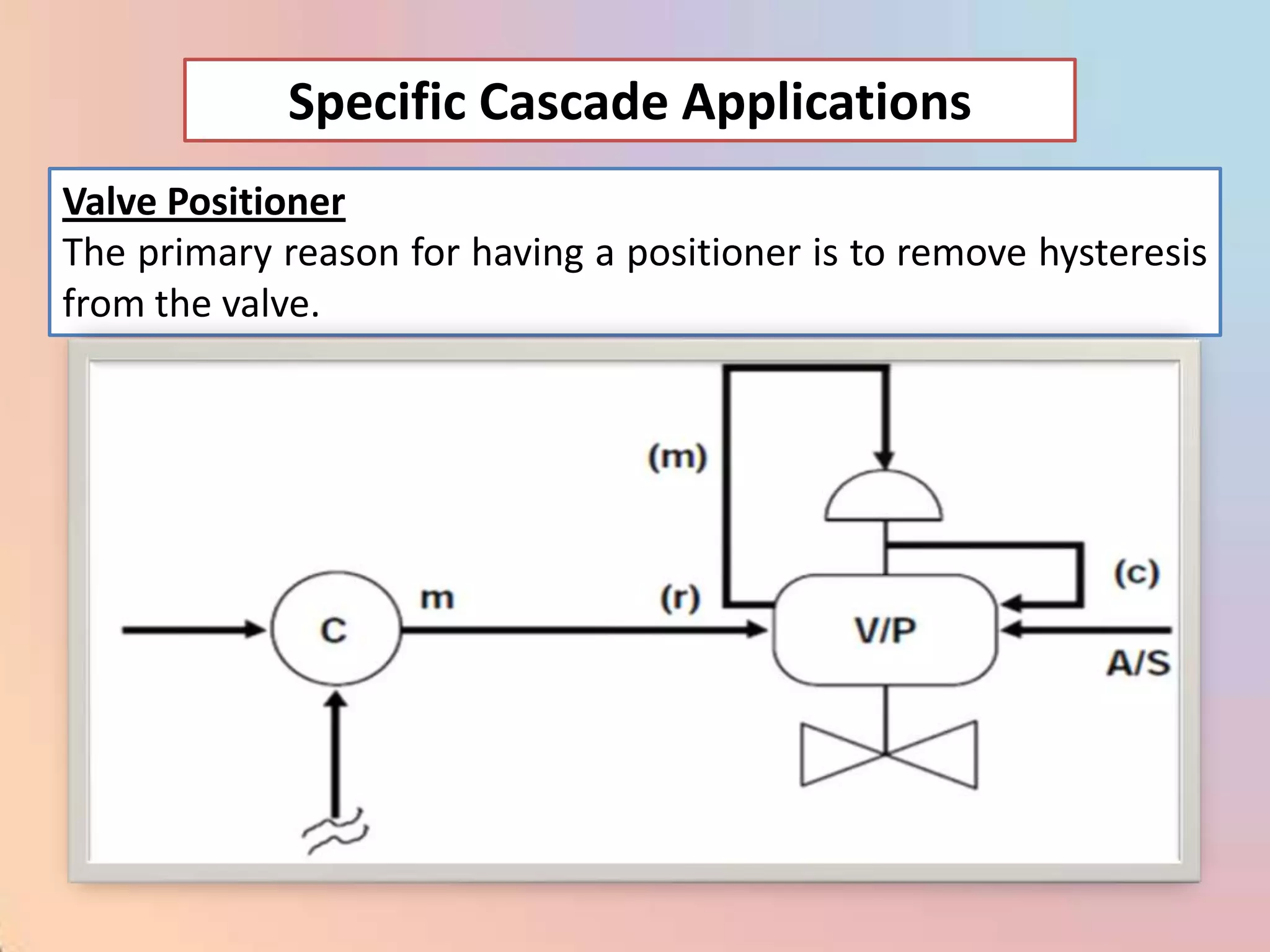
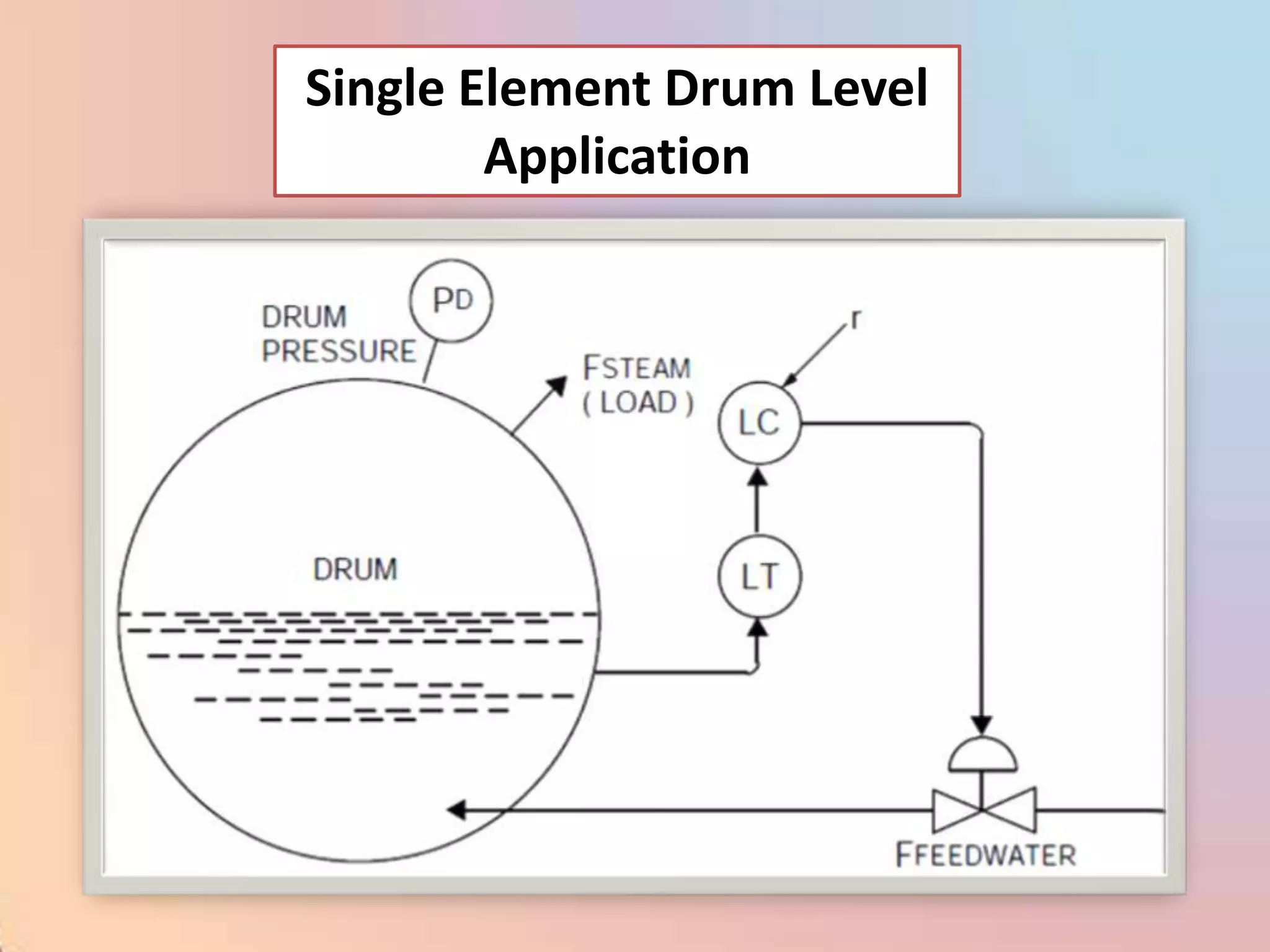
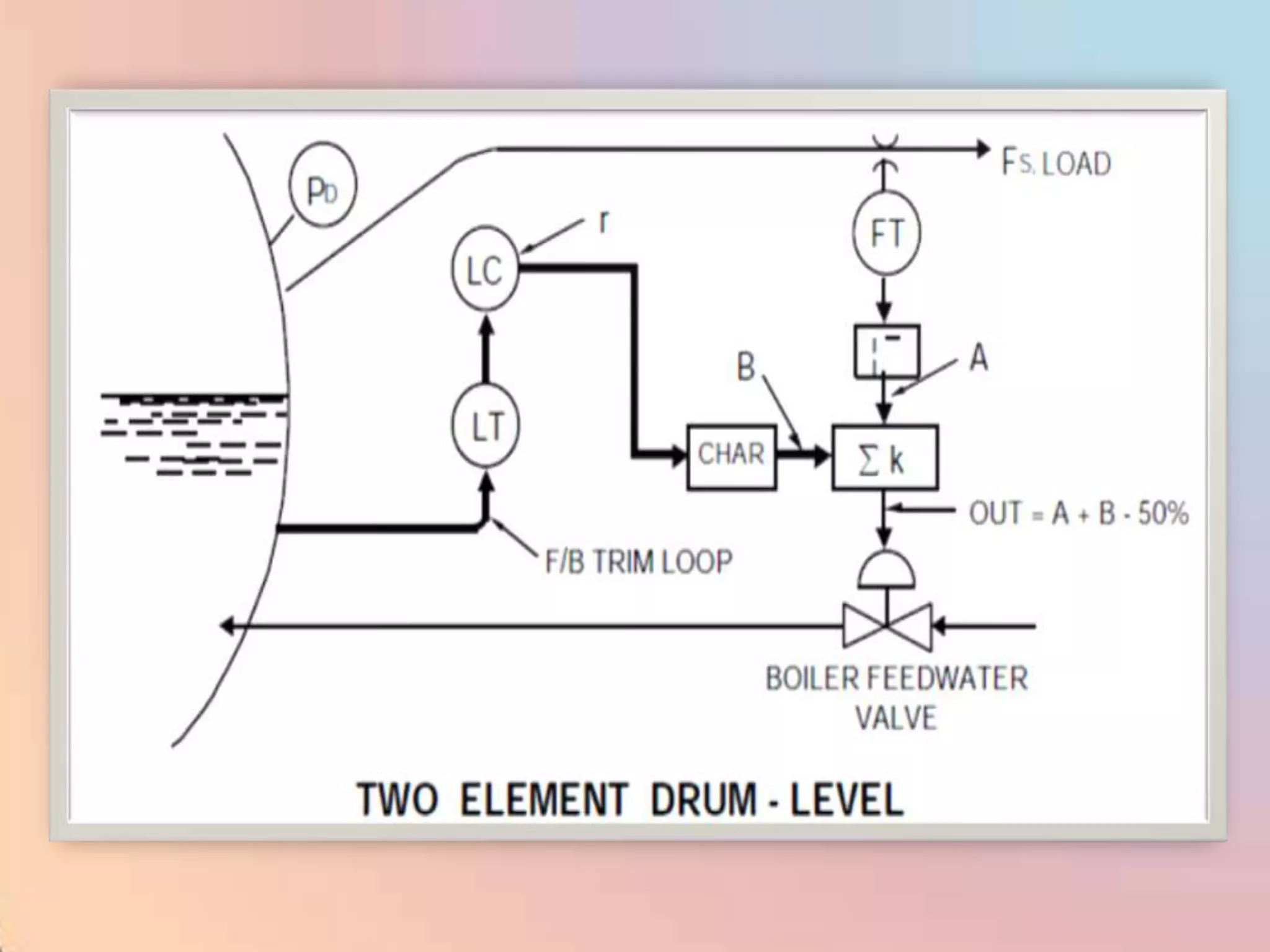
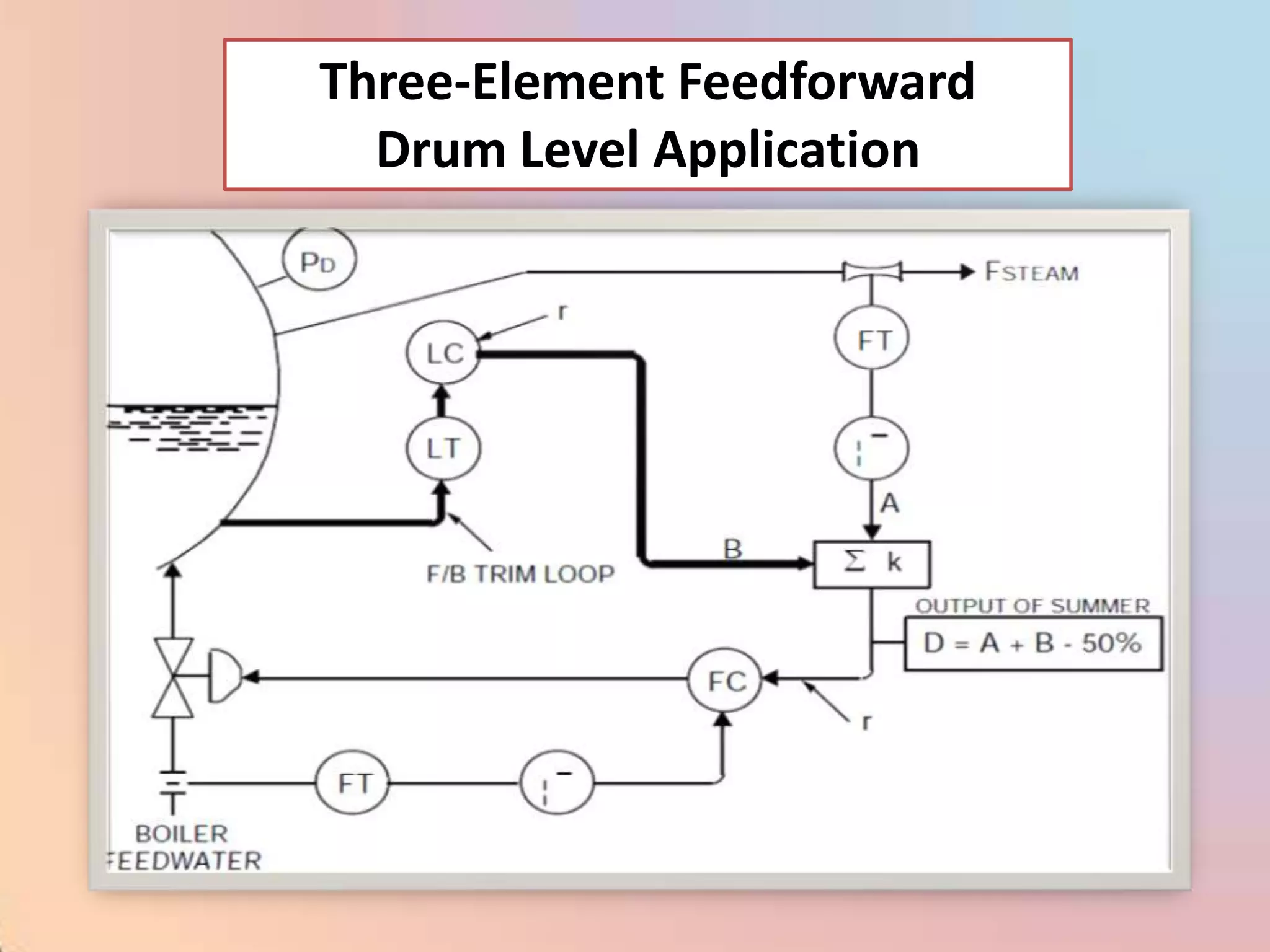
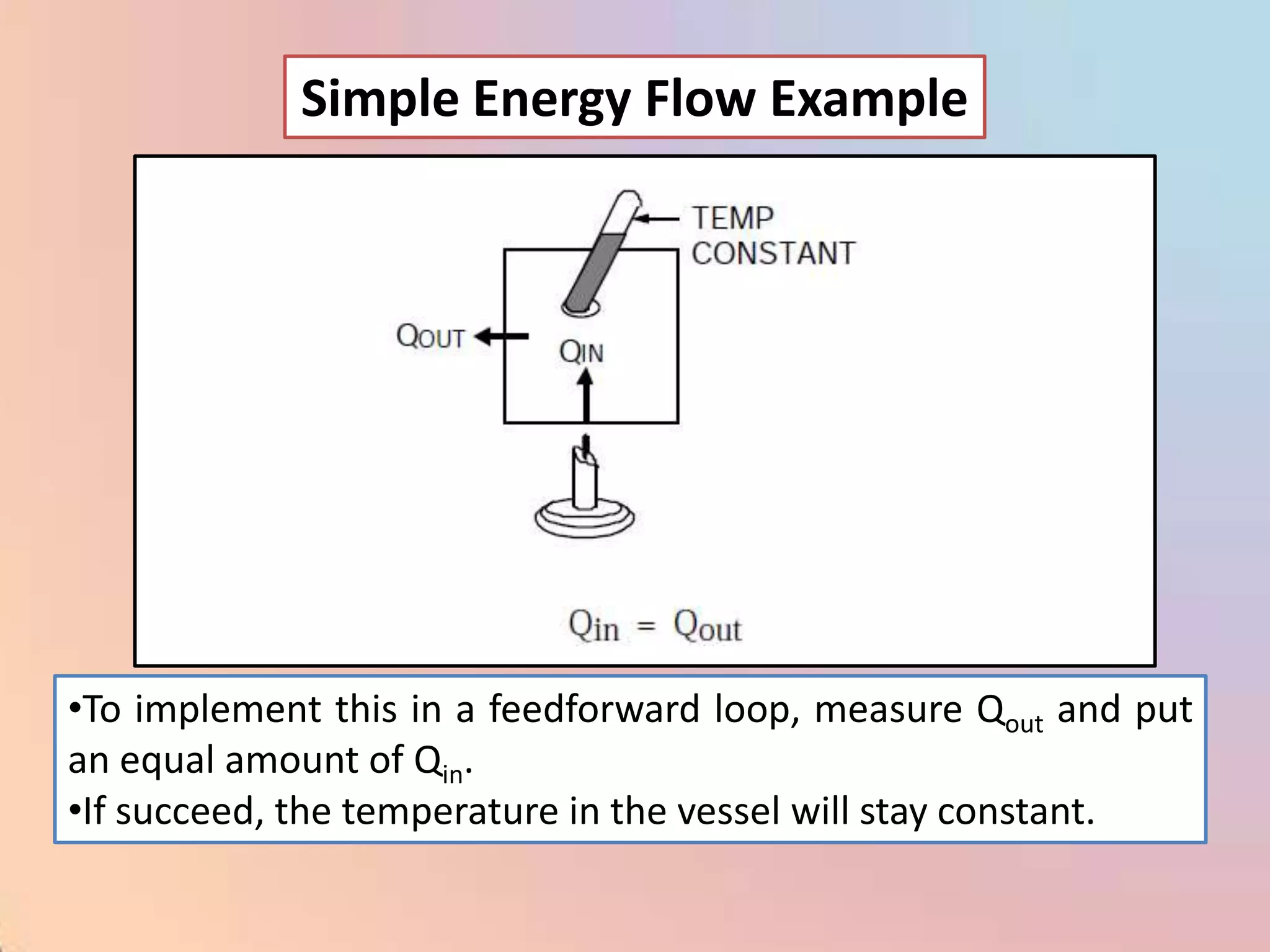
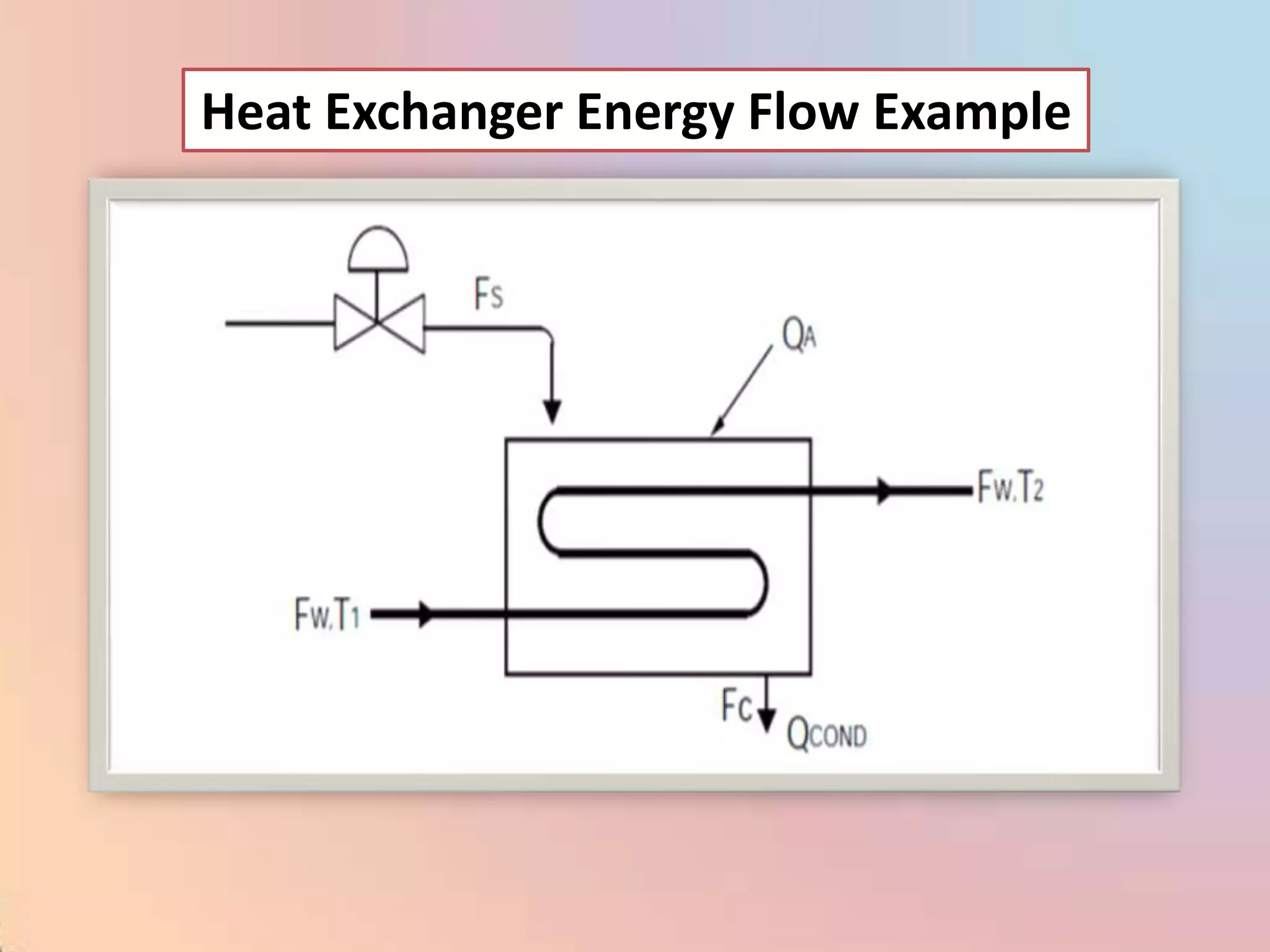
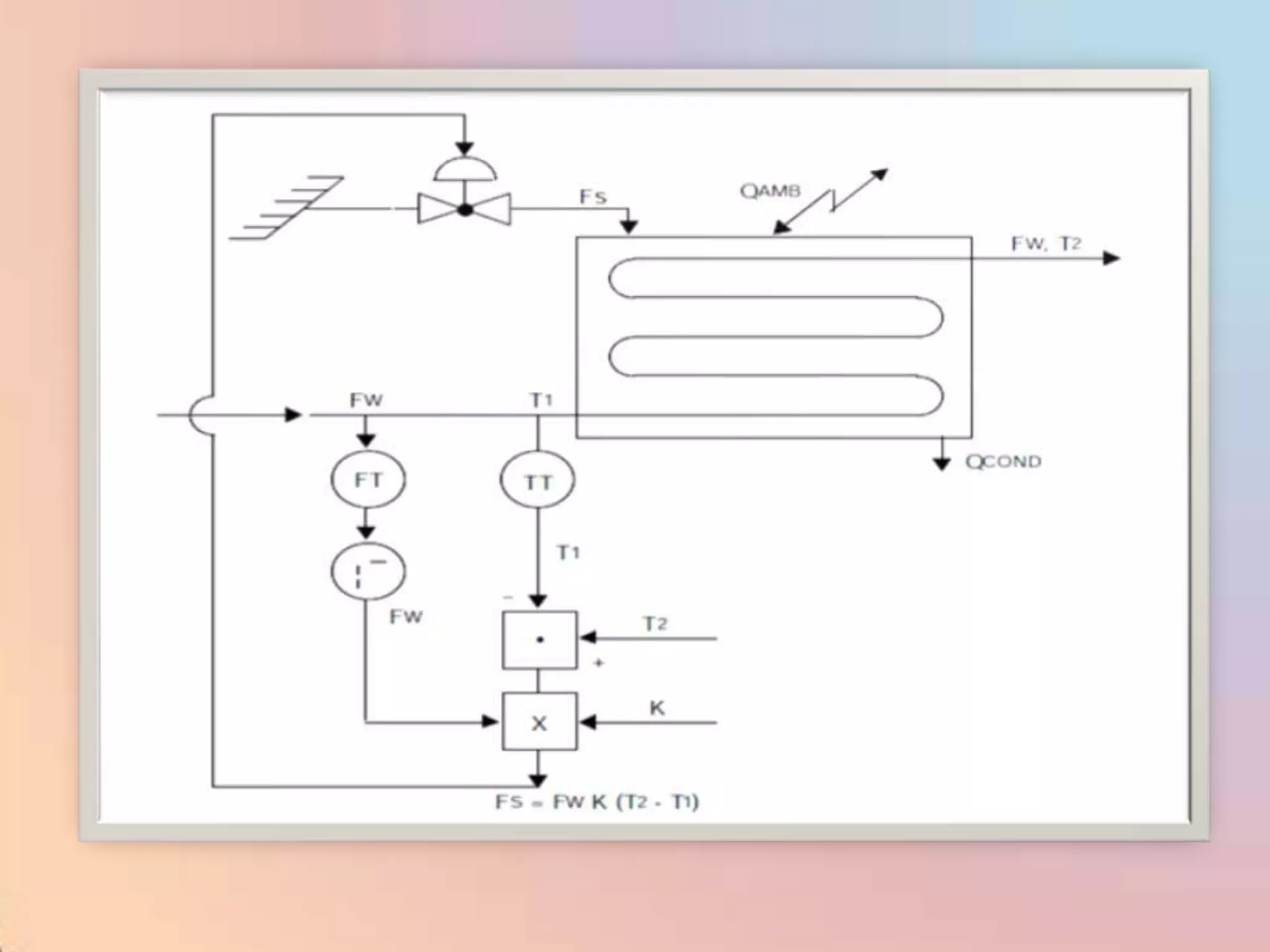
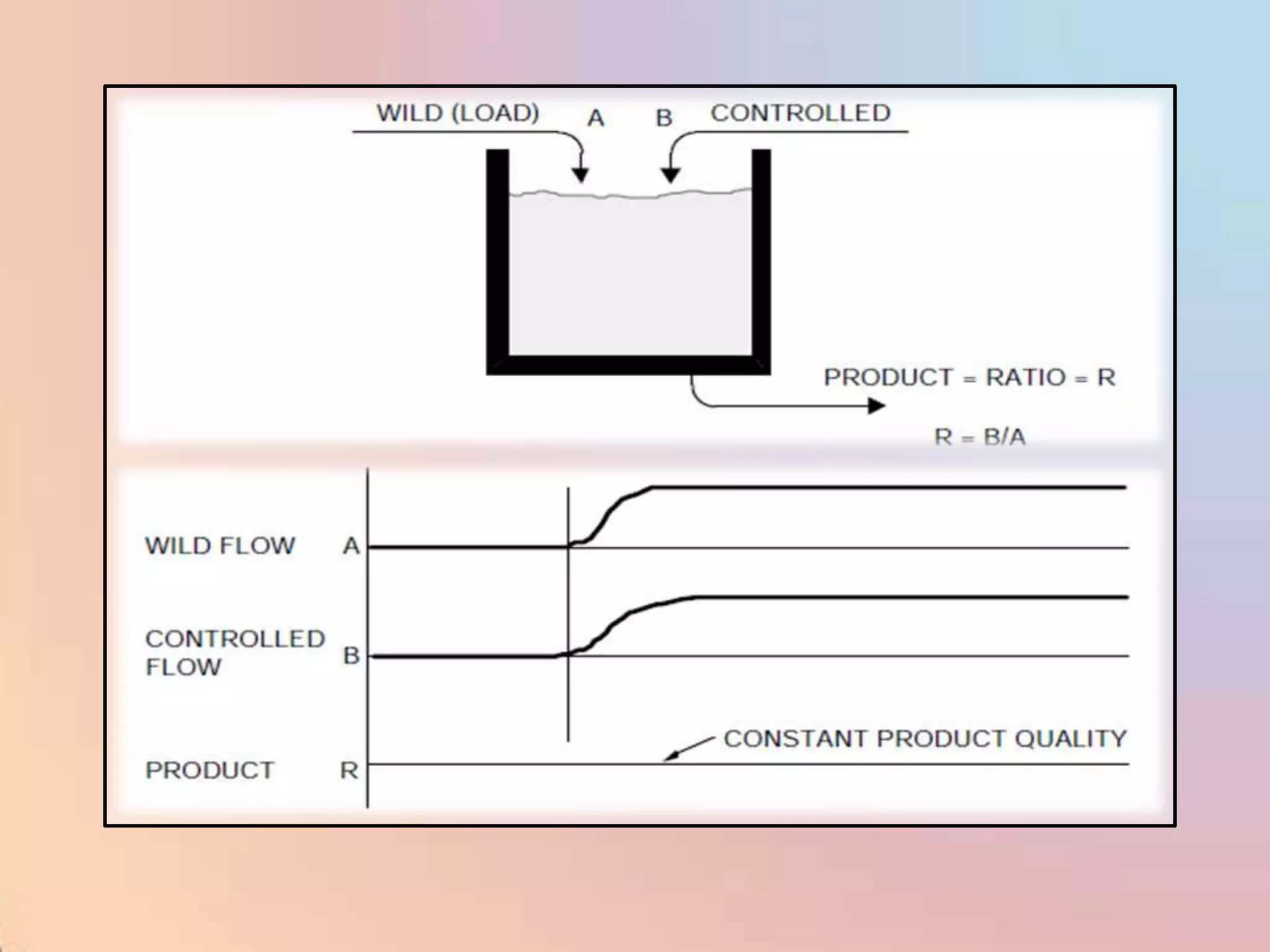
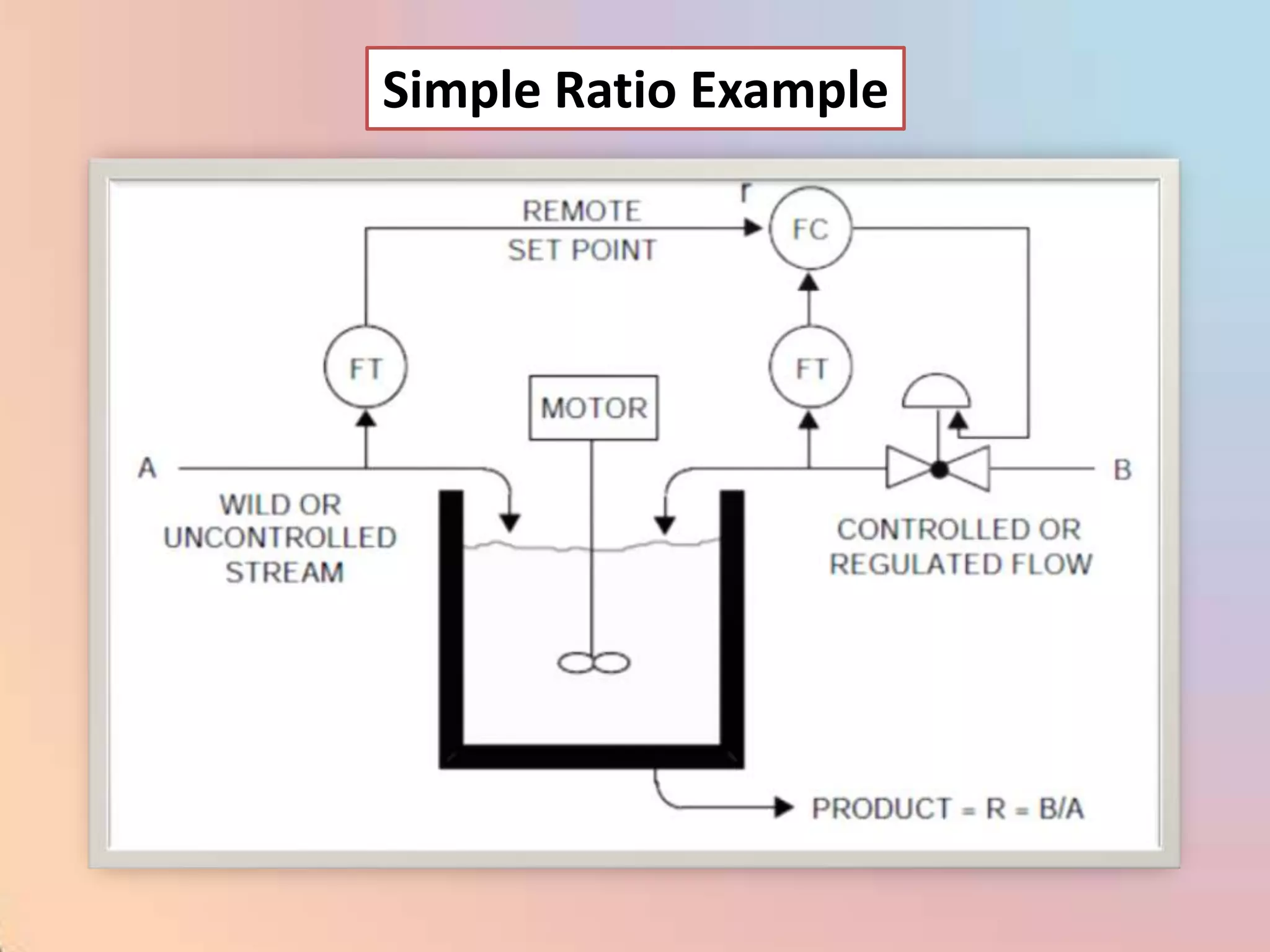
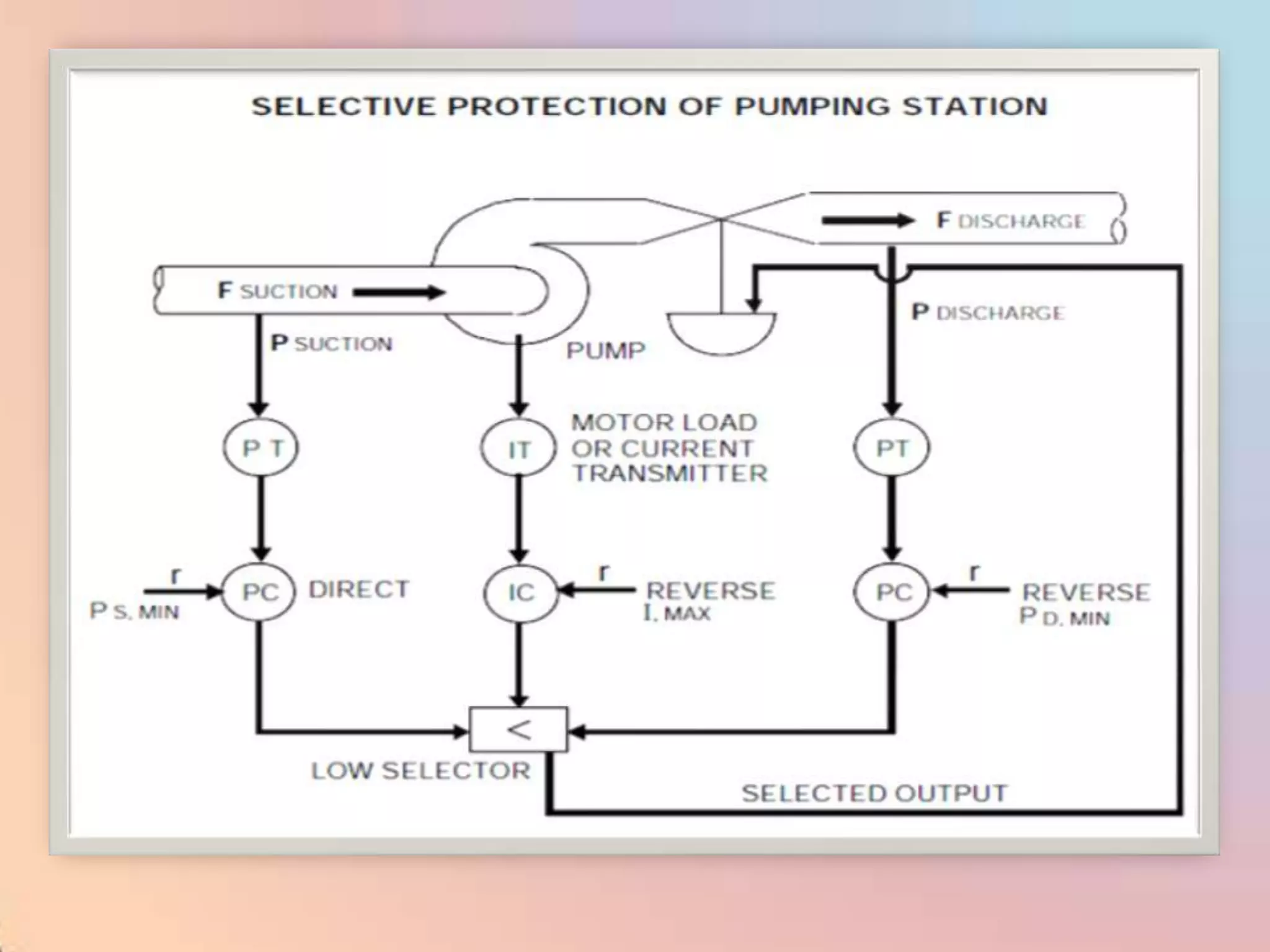
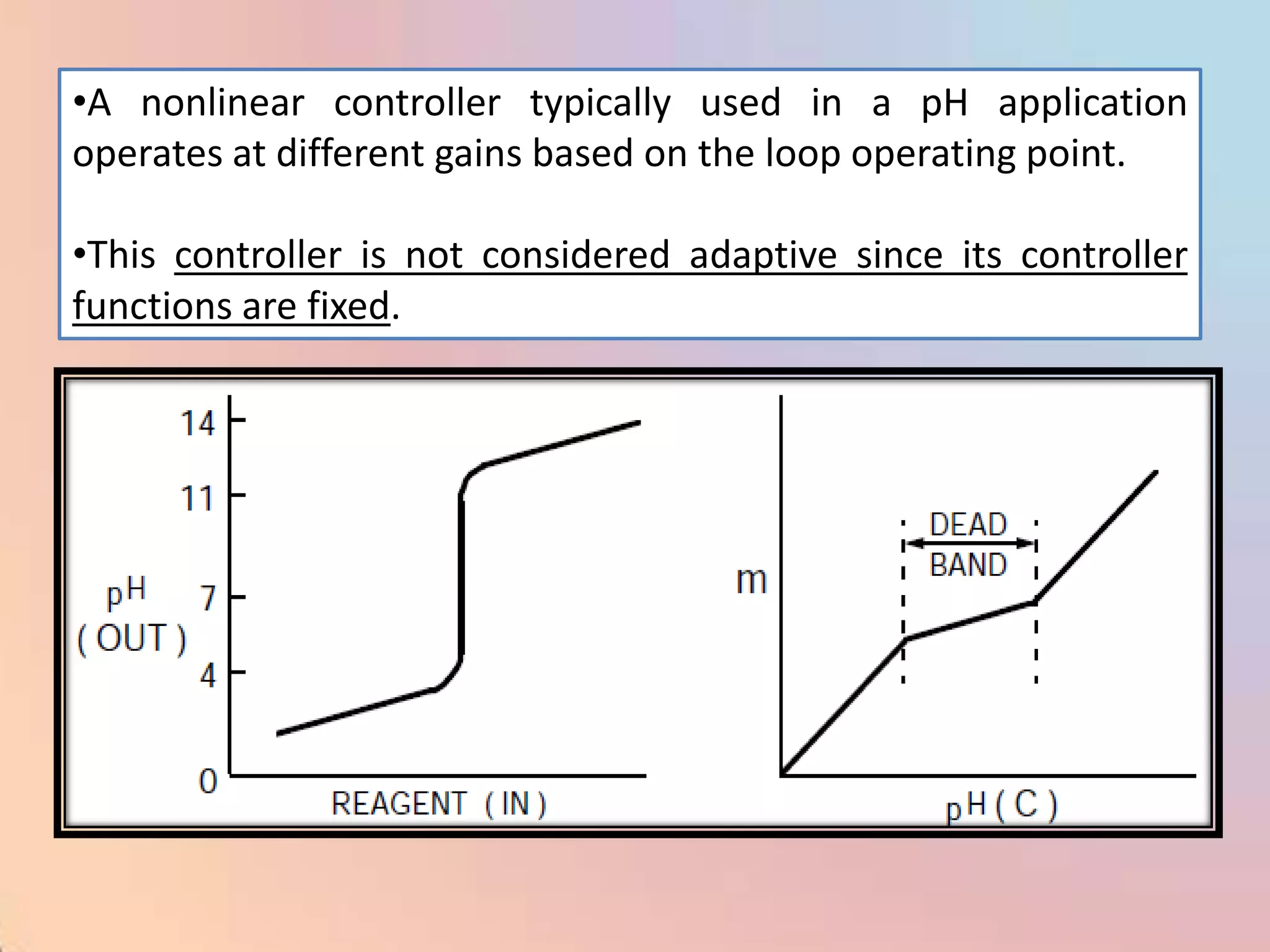
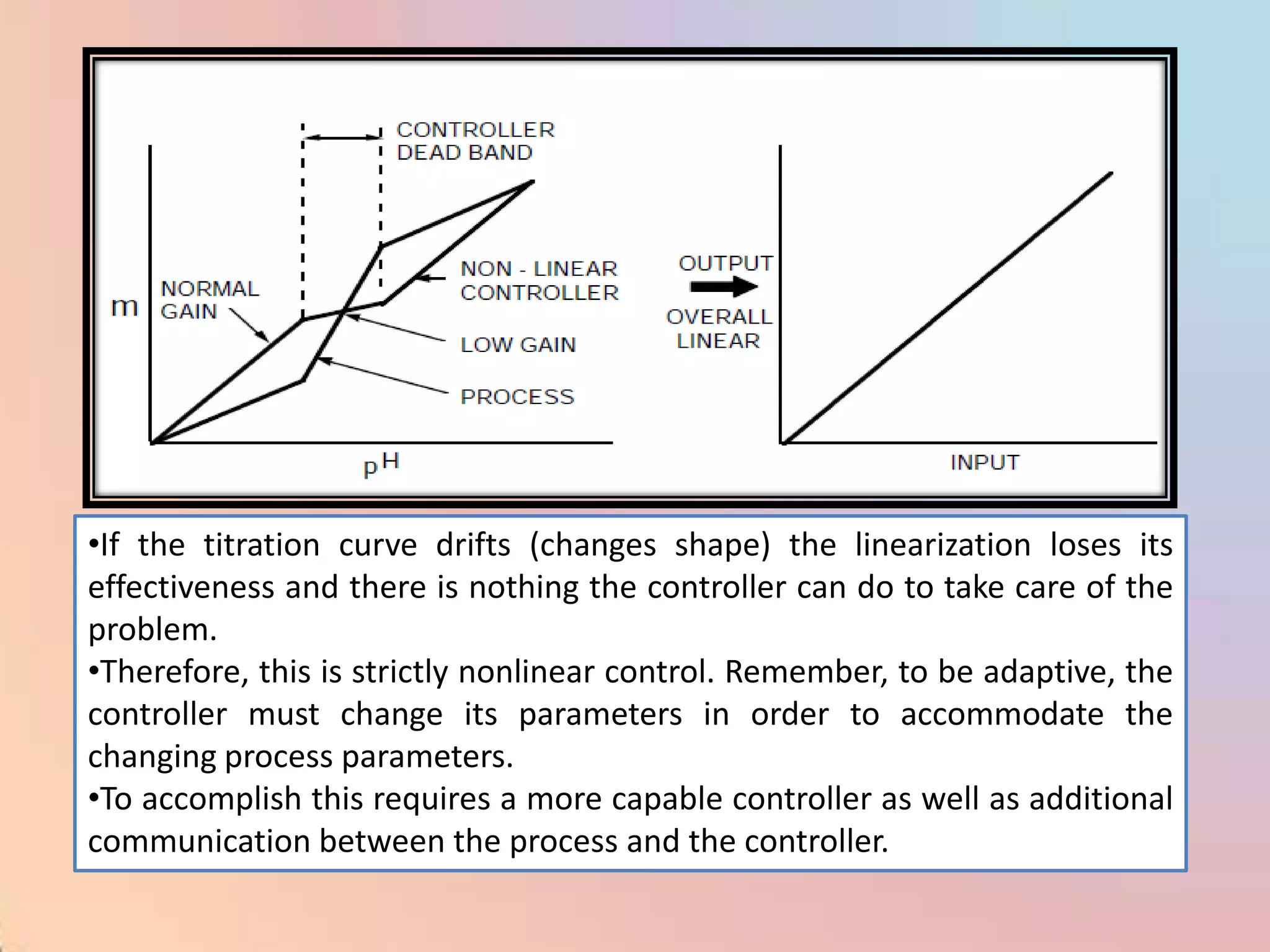
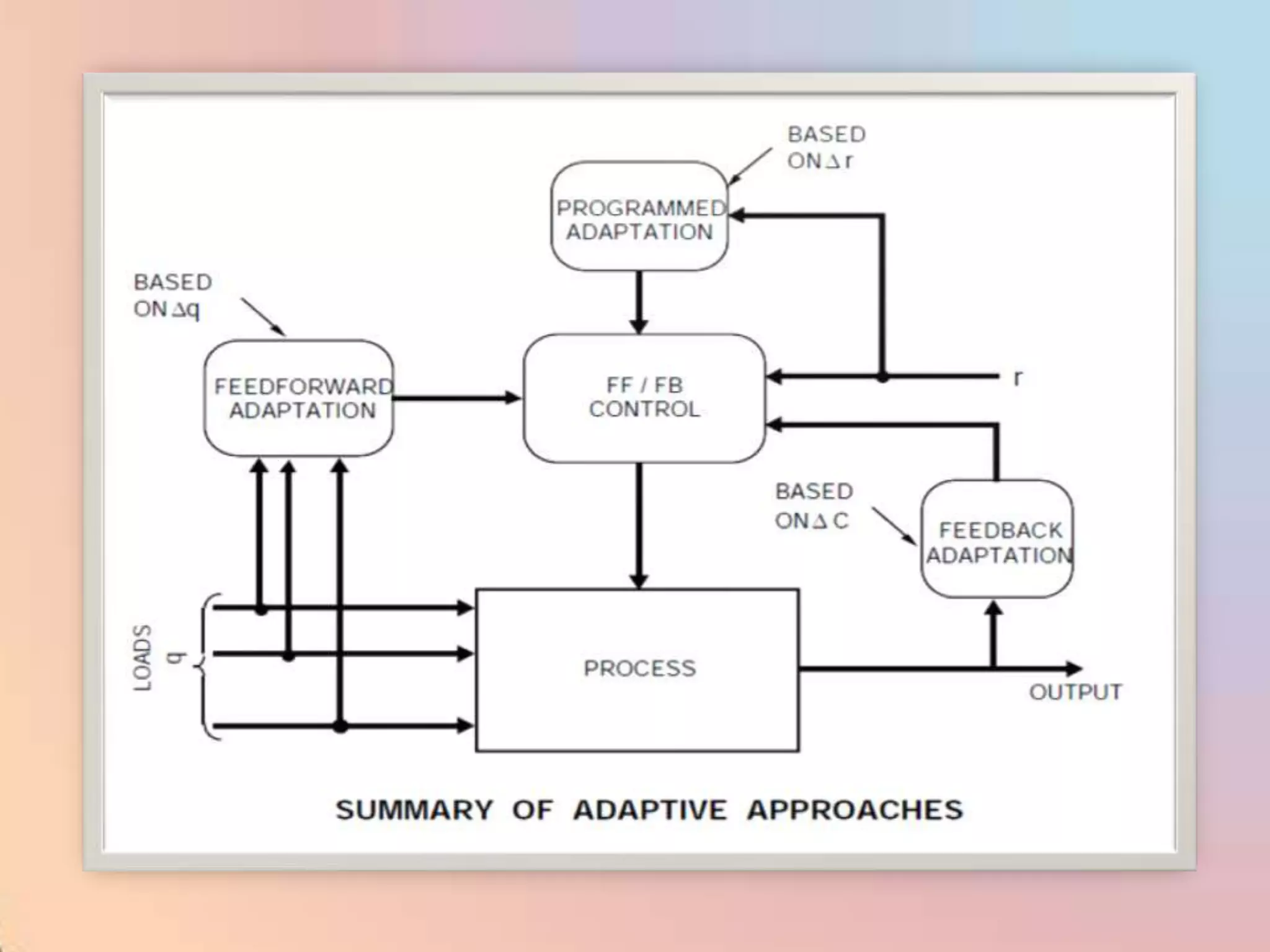
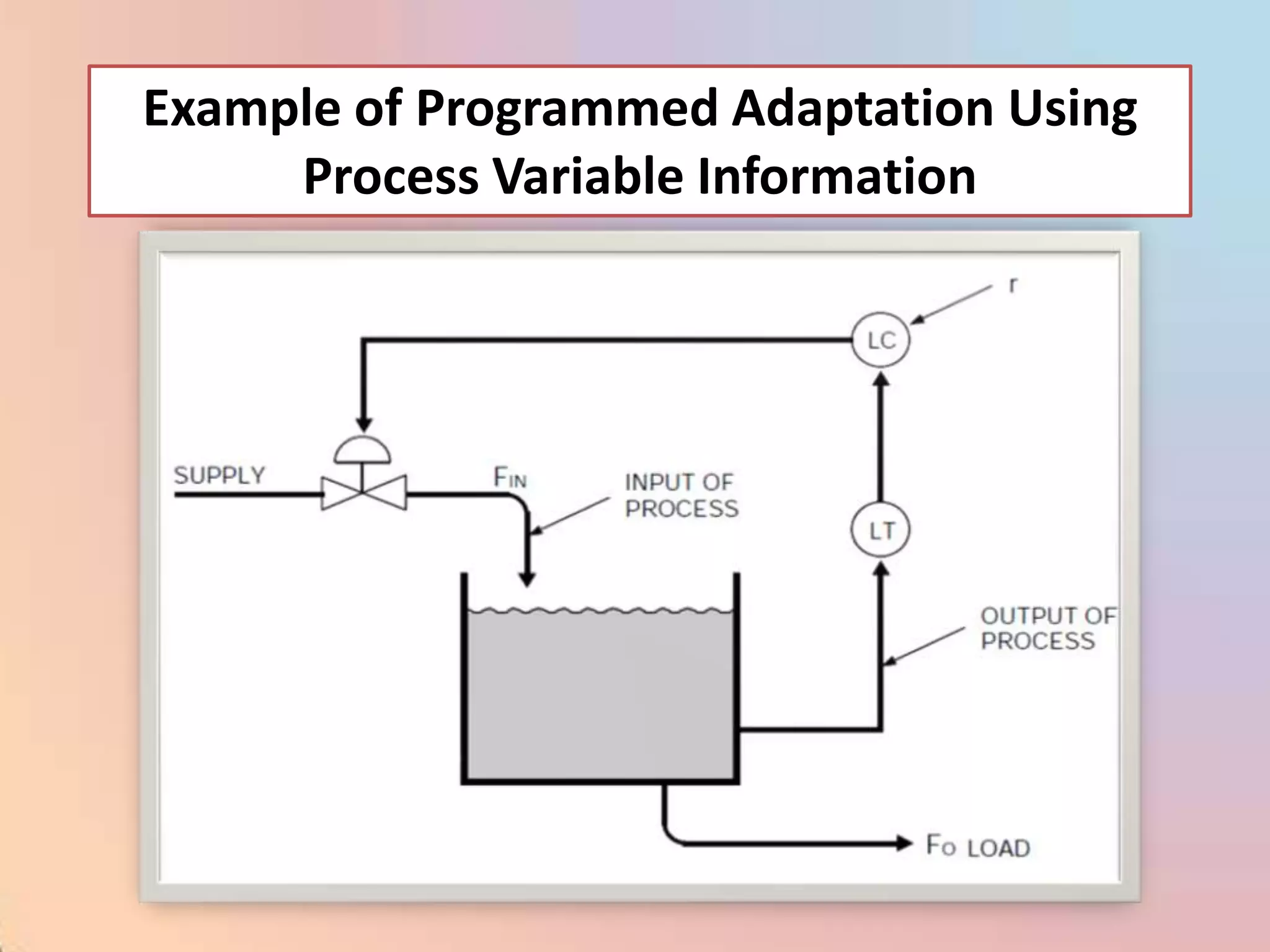
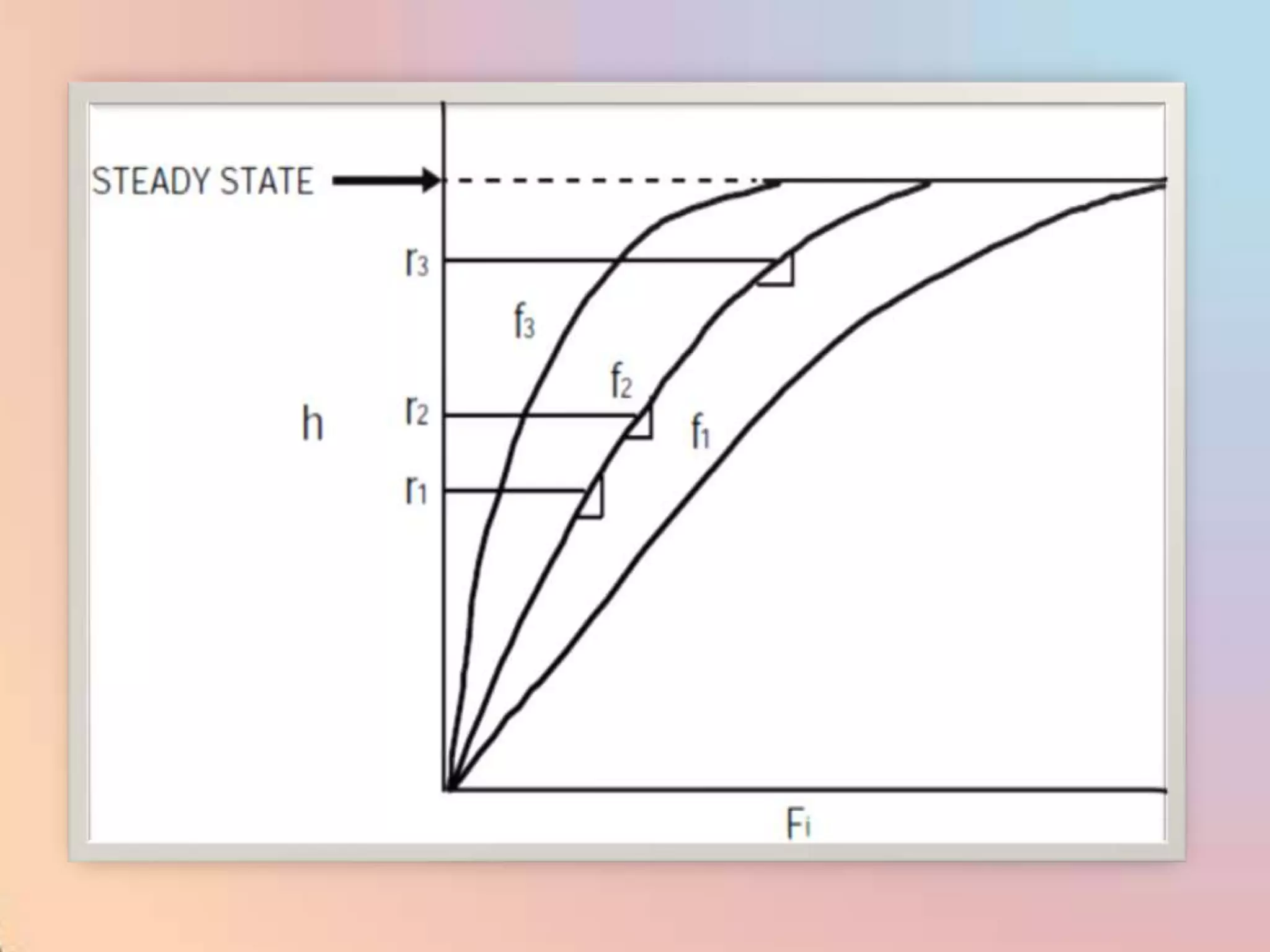
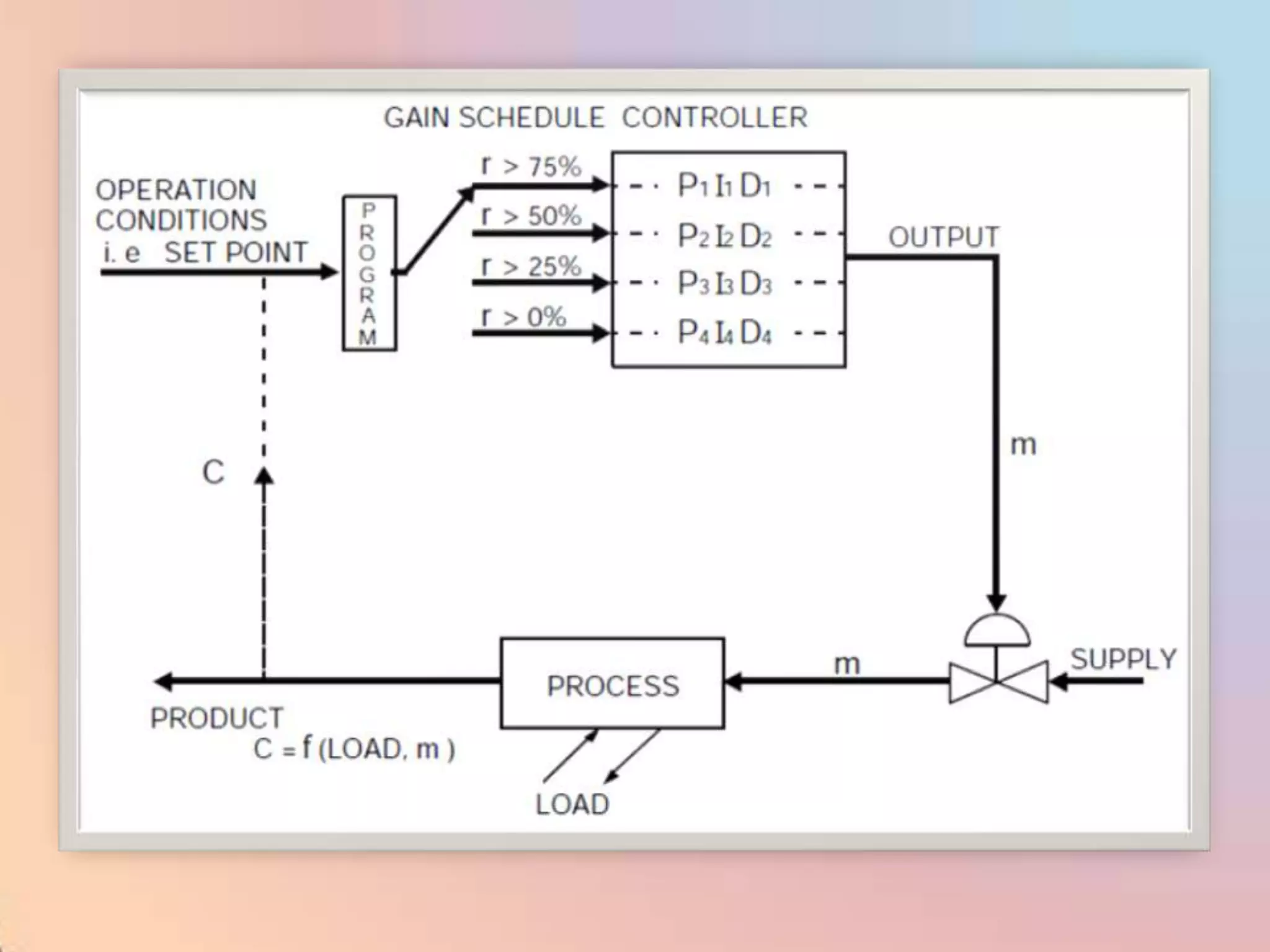
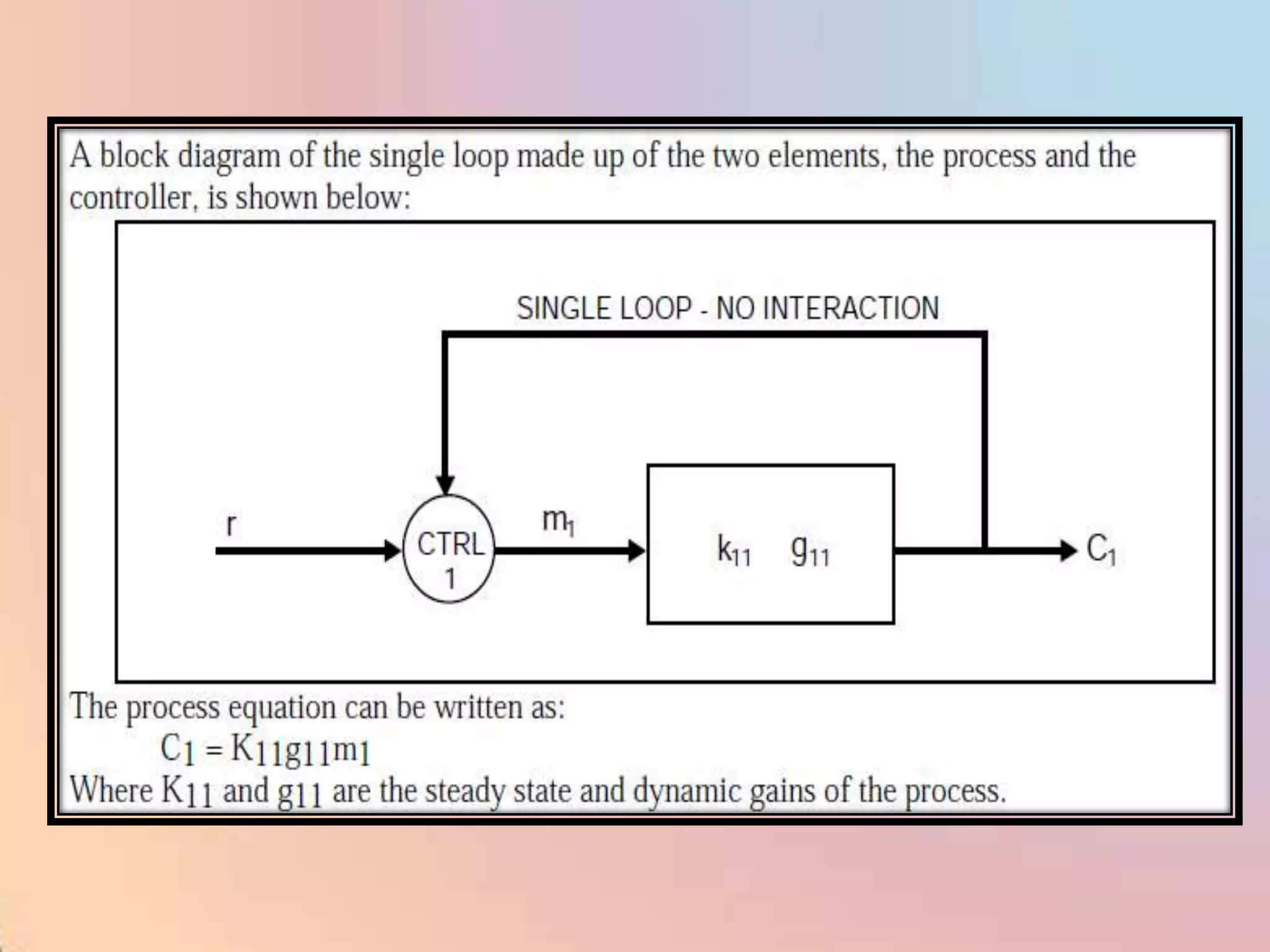
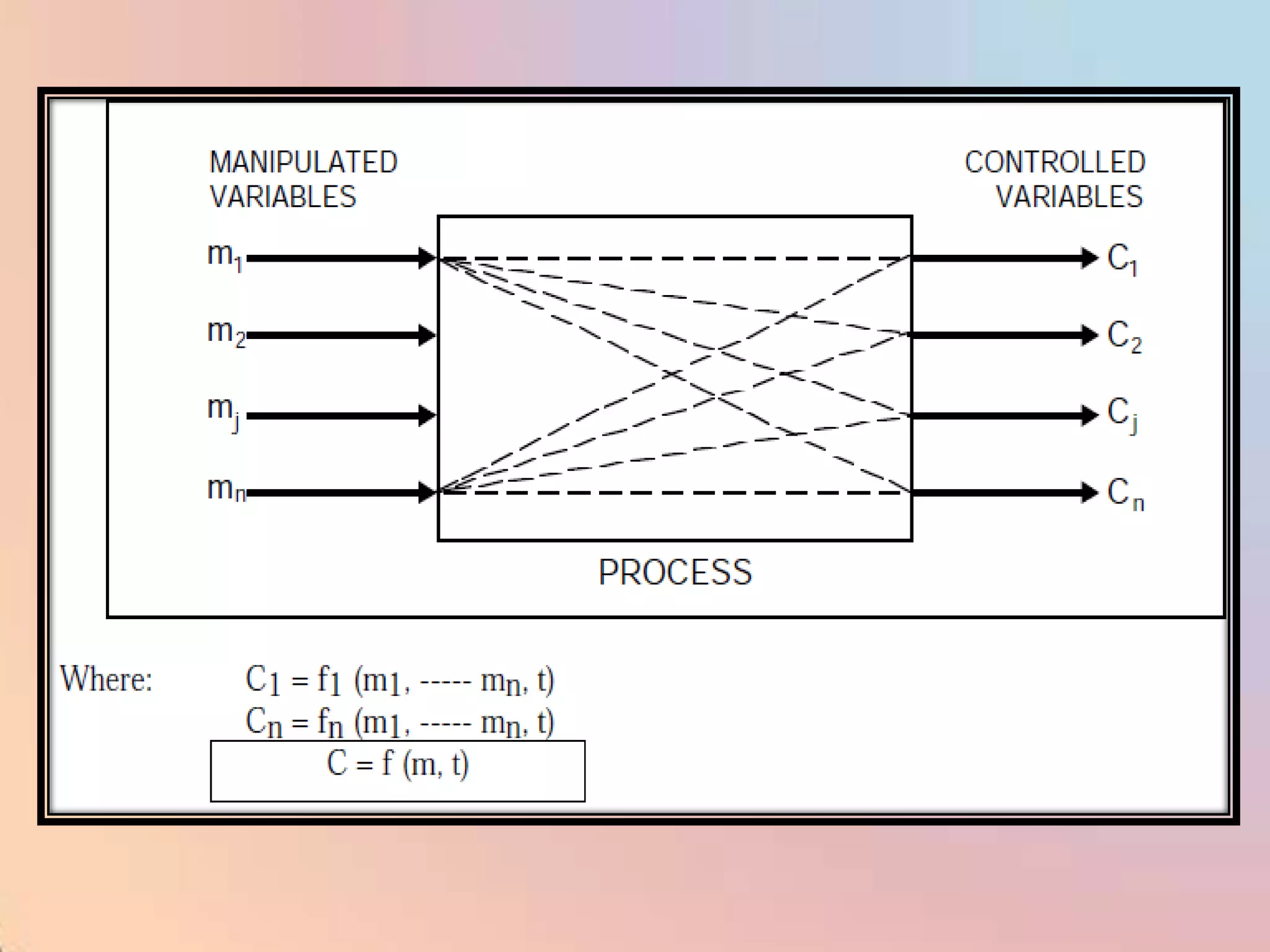
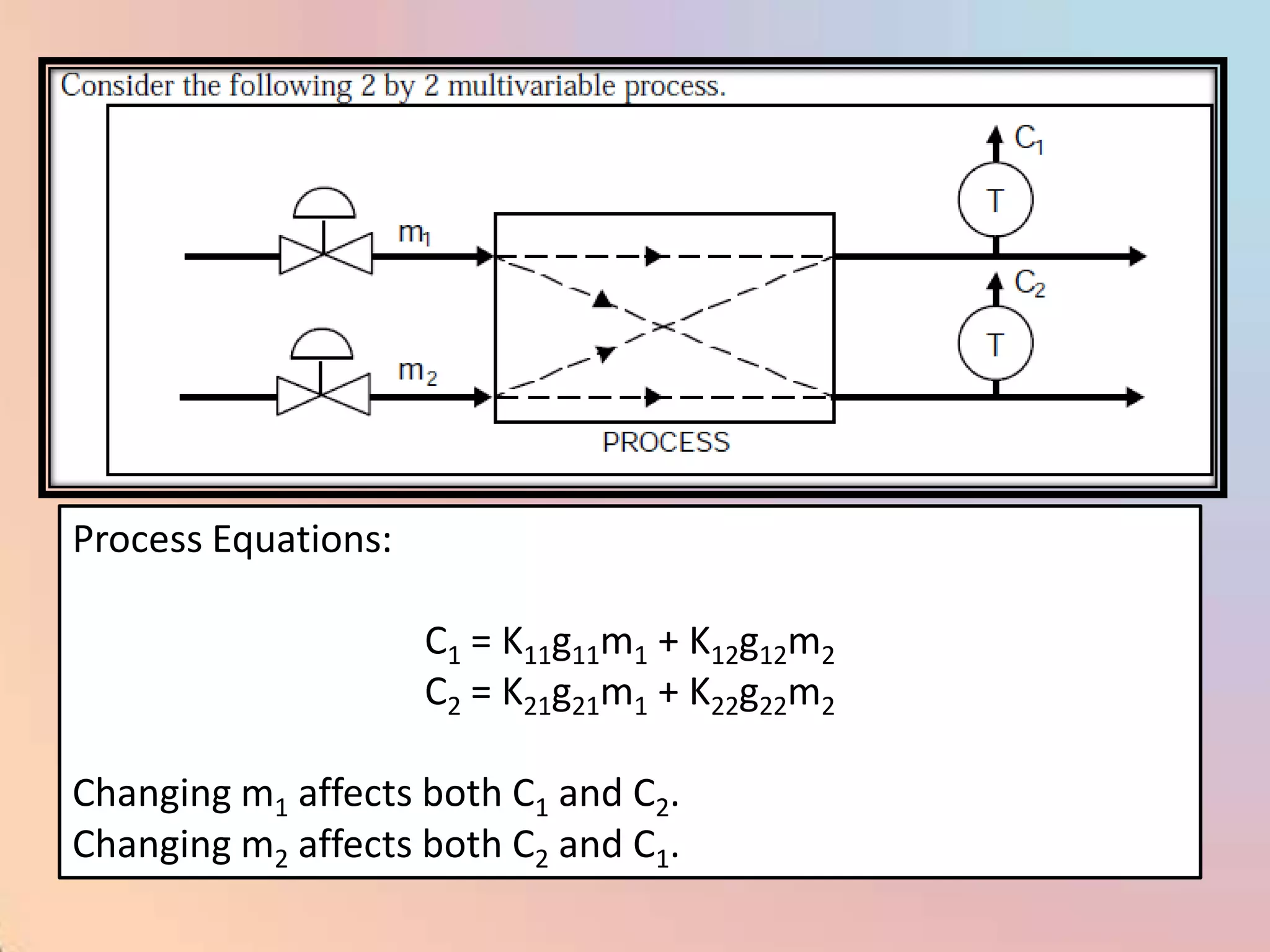
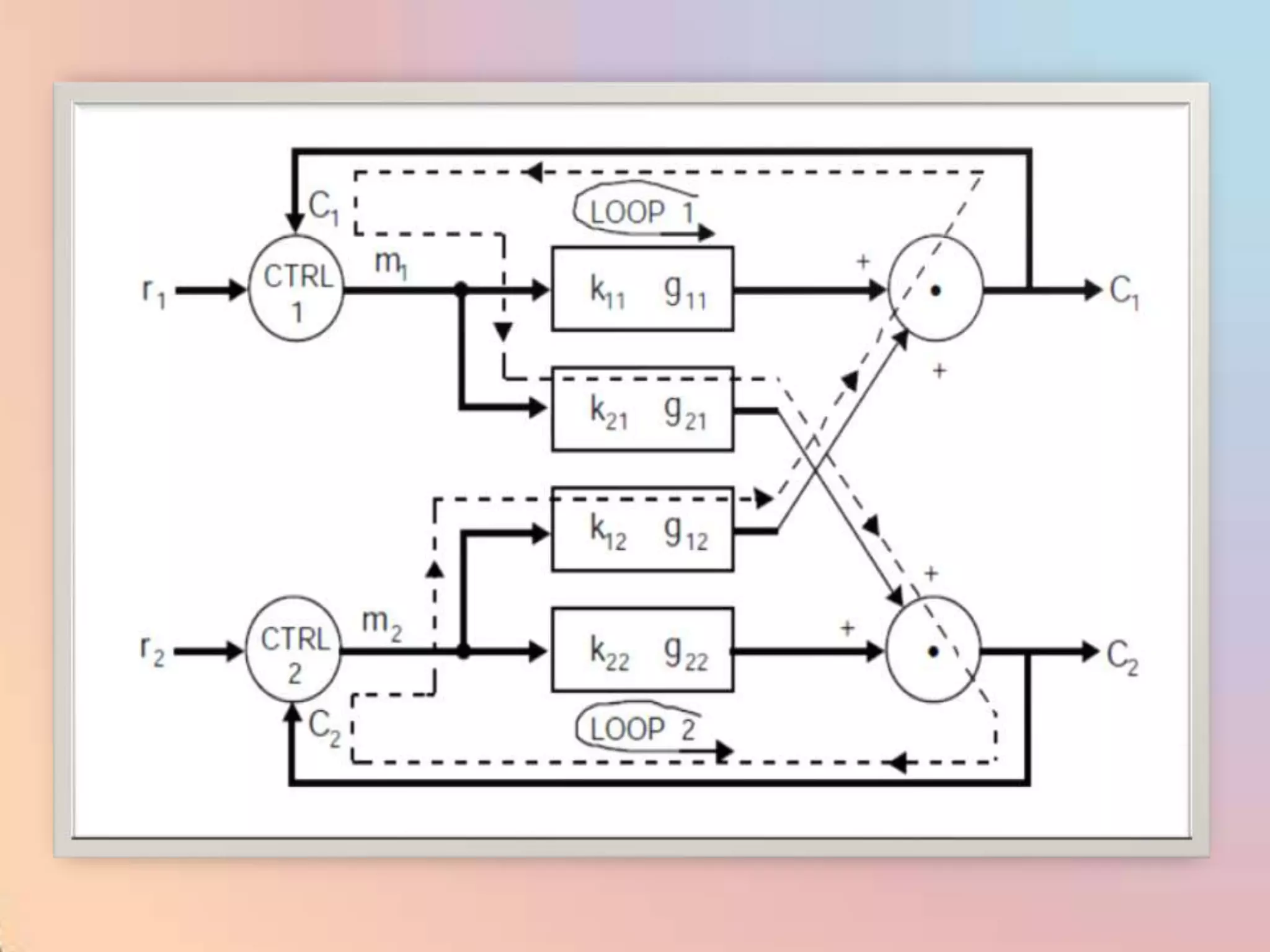
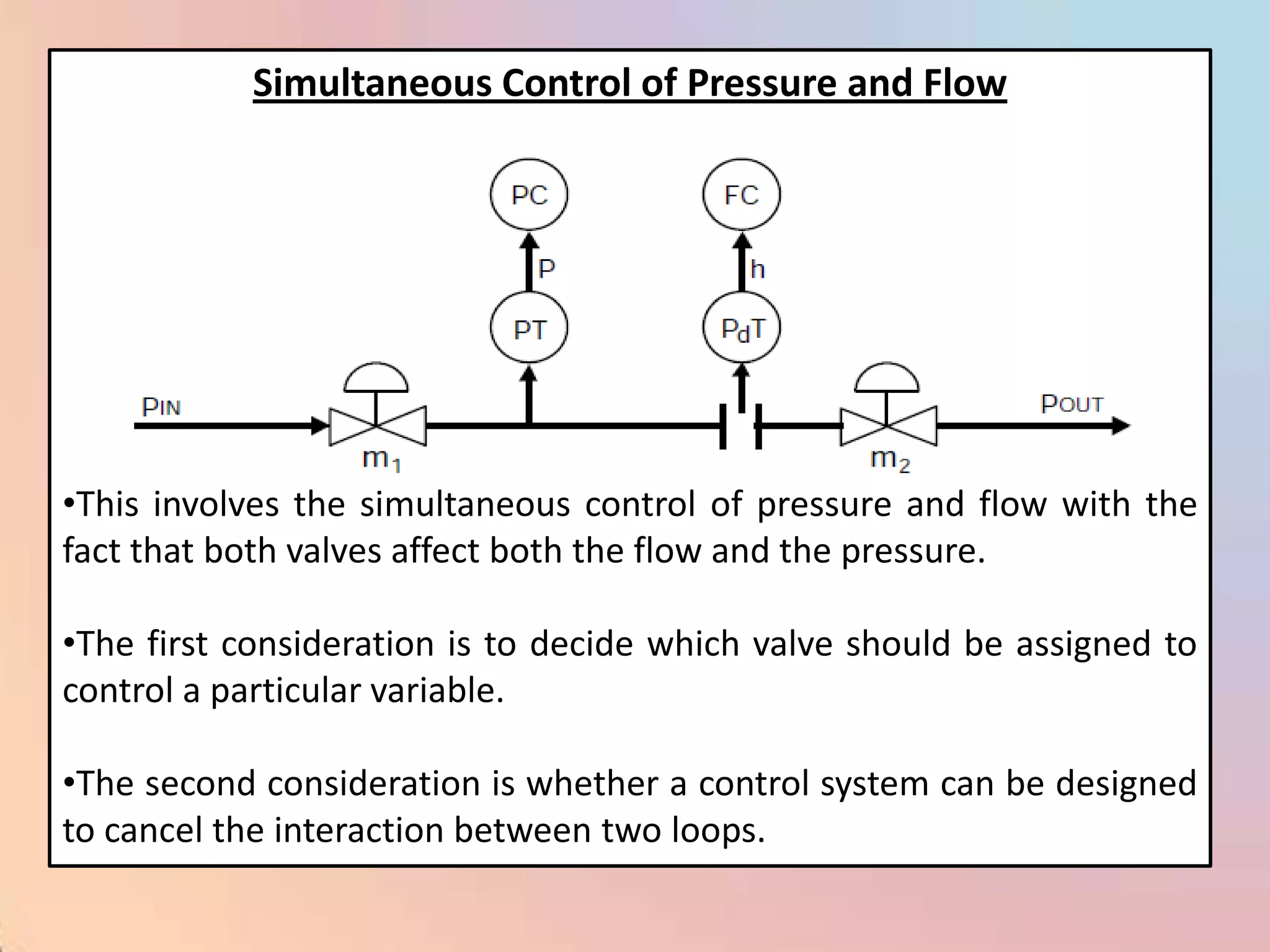
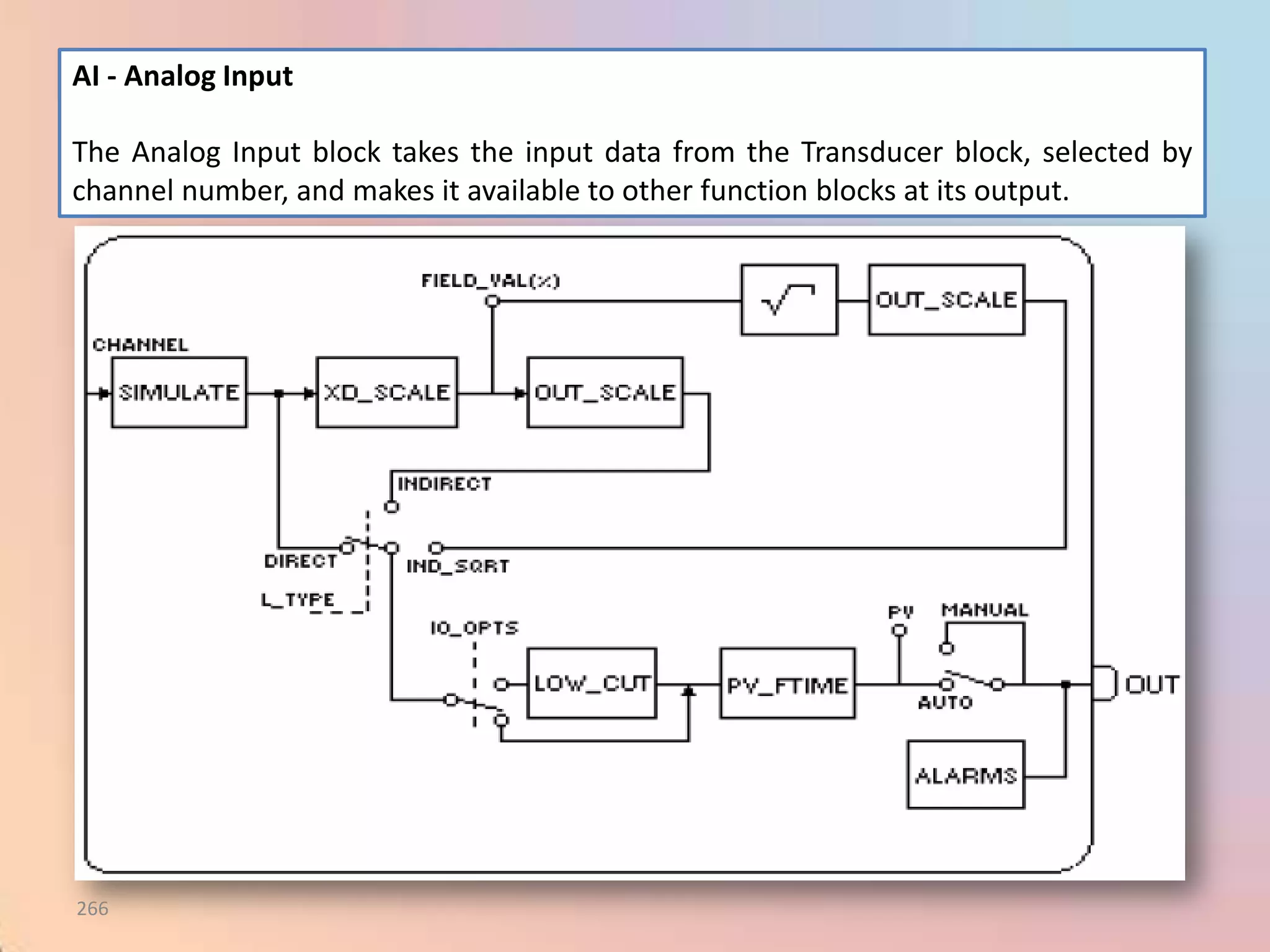
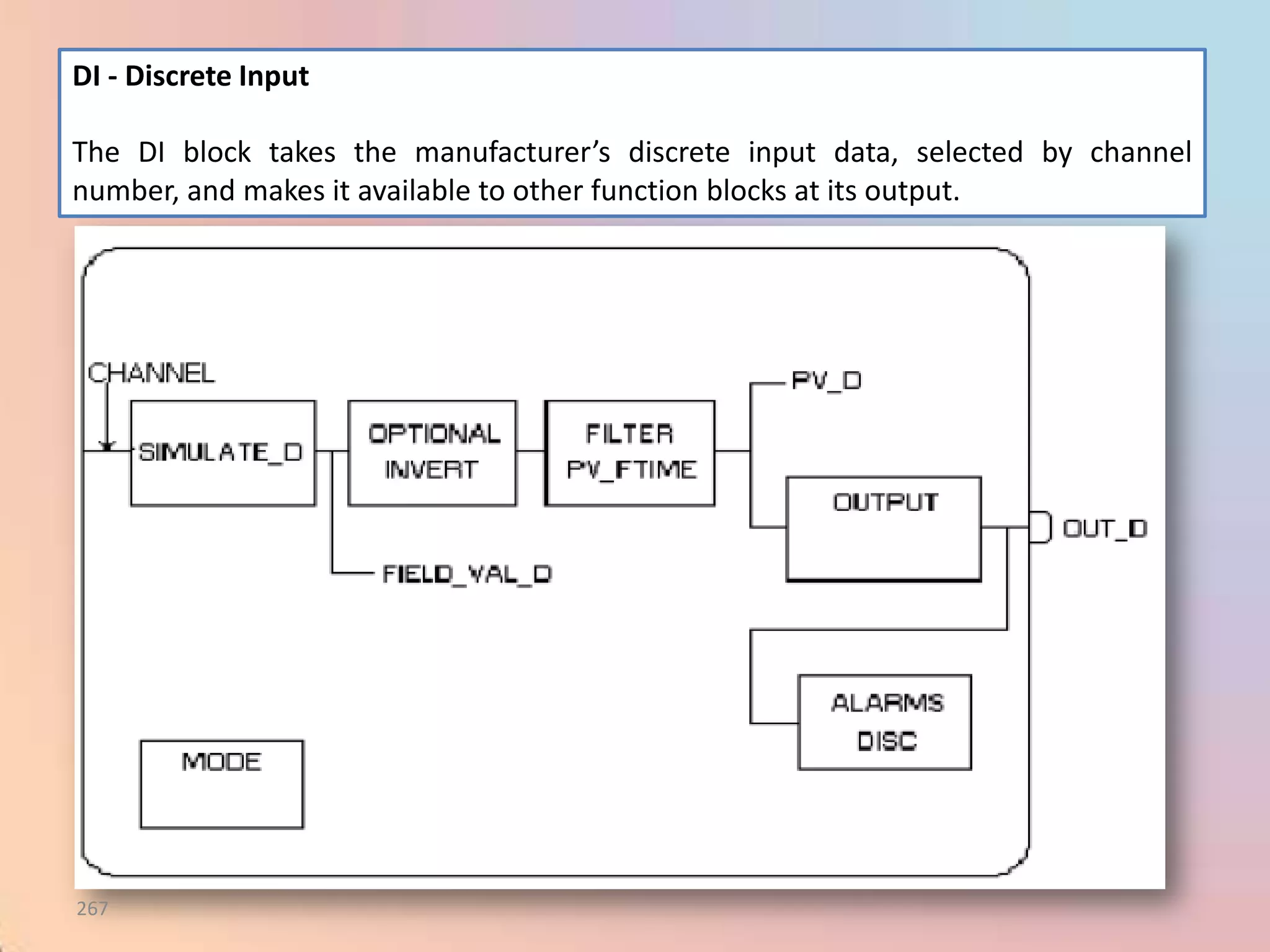
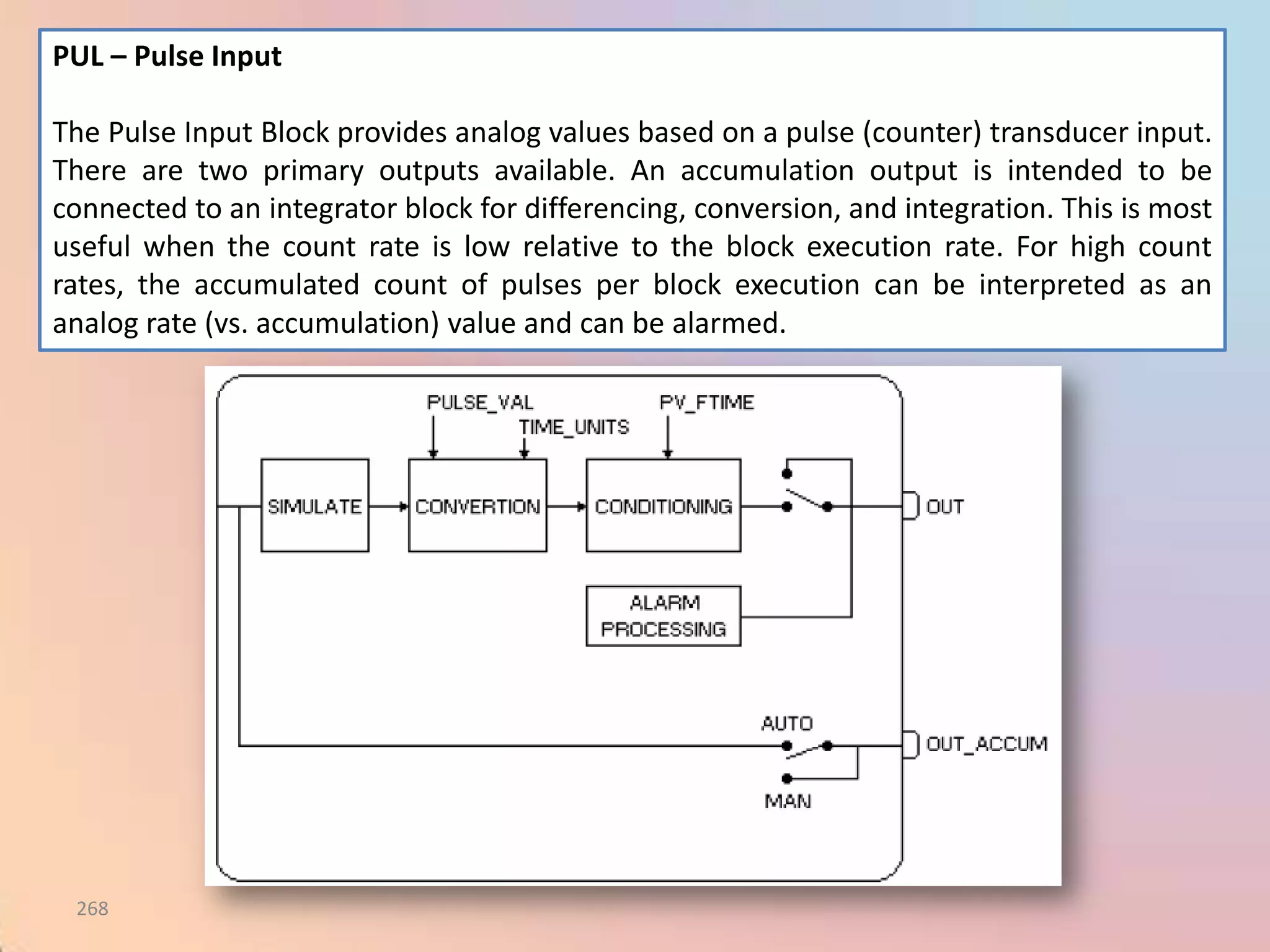
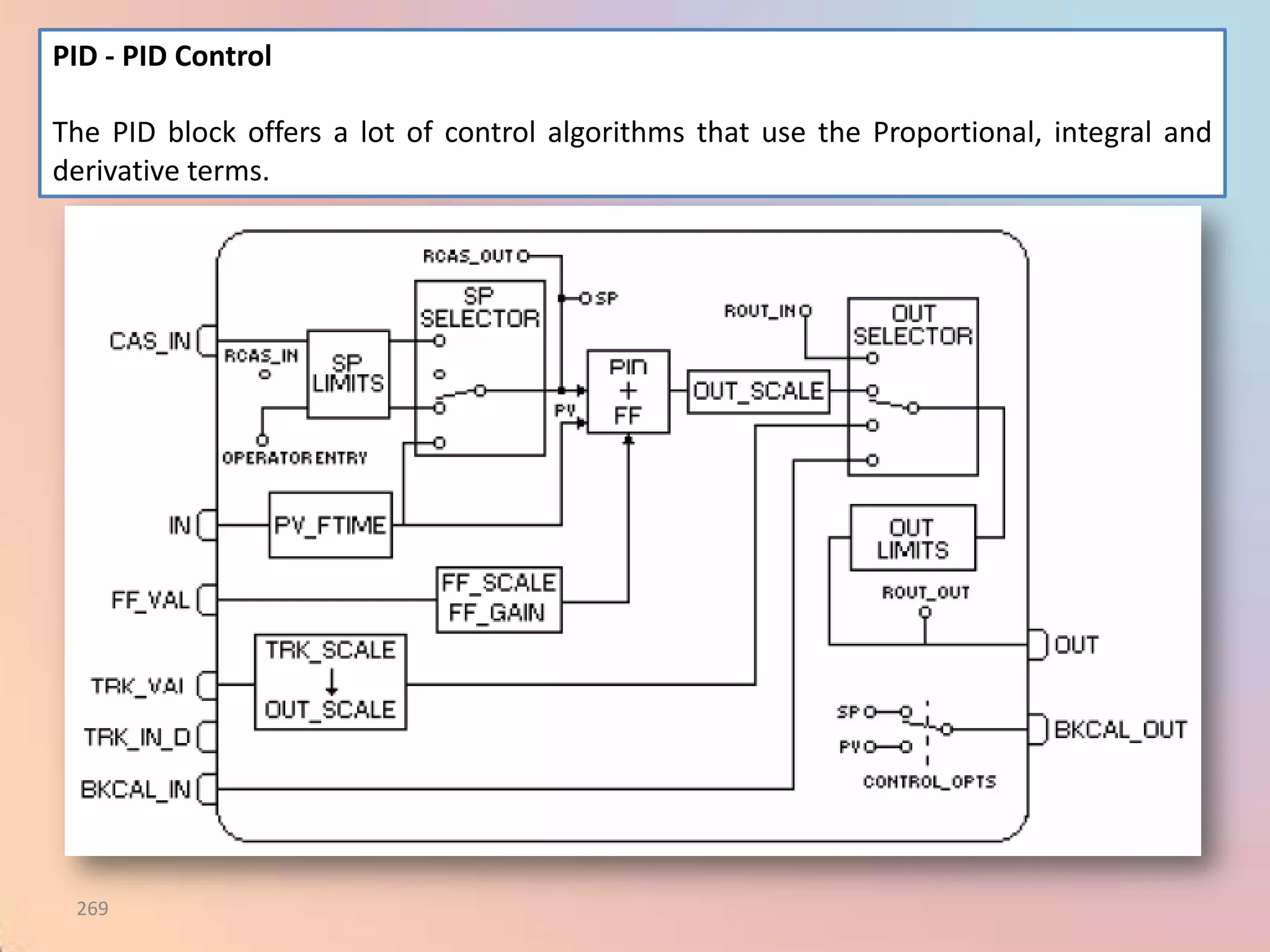
The document provides an extensive overview of process control, including definitions of key terms, types of control modes (open-loop, closed-loop, feedback, and feedforward), and various control algorithms like PID. It emphasizes the importance of choosing the right control strategy to maintain product quality, optimize energy use, and ensure safety. Additionally, it discusses the characteristics and performance aspects of control elements such as valves and transmitters in controlling mass and energy processes.
































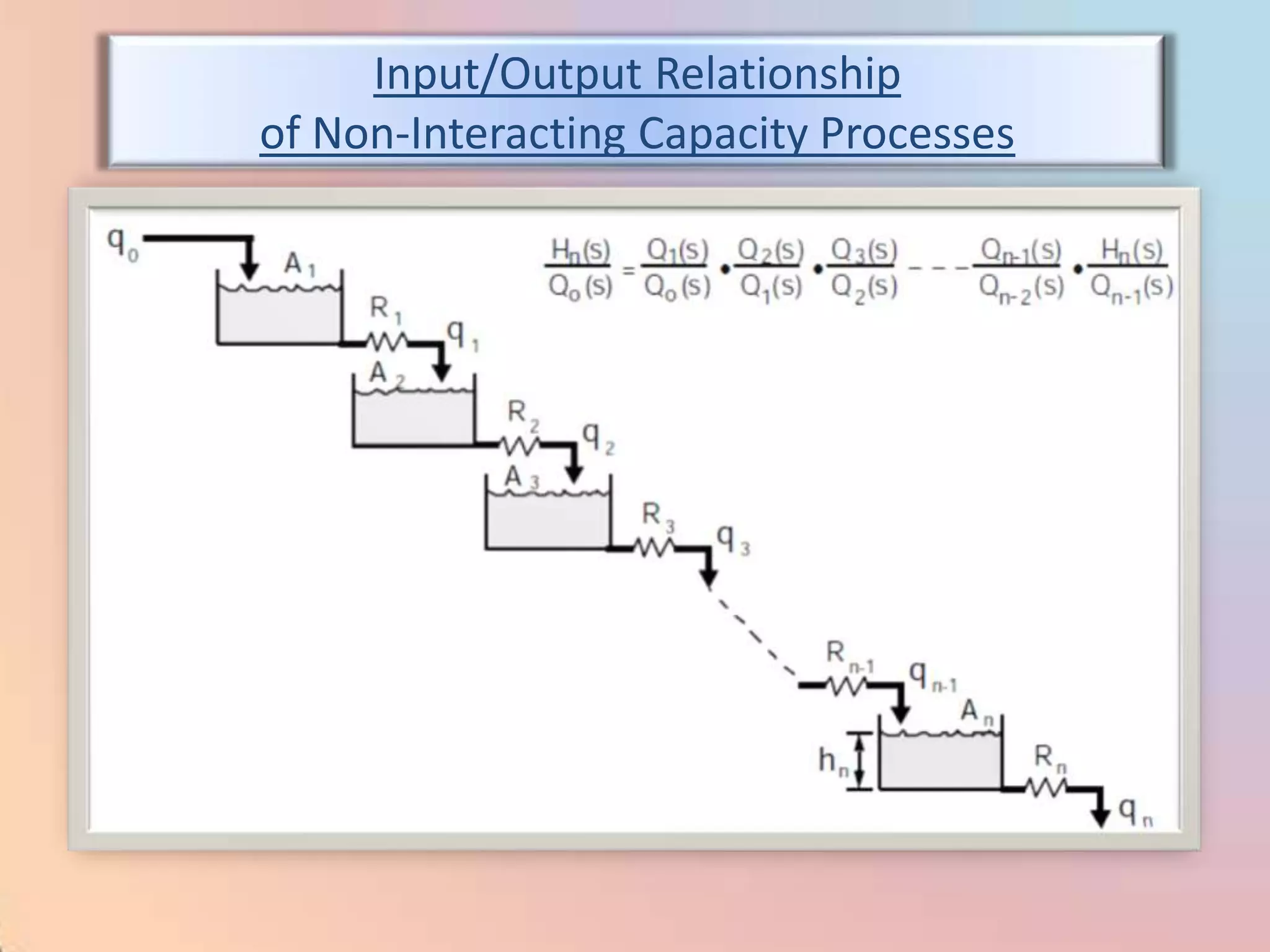
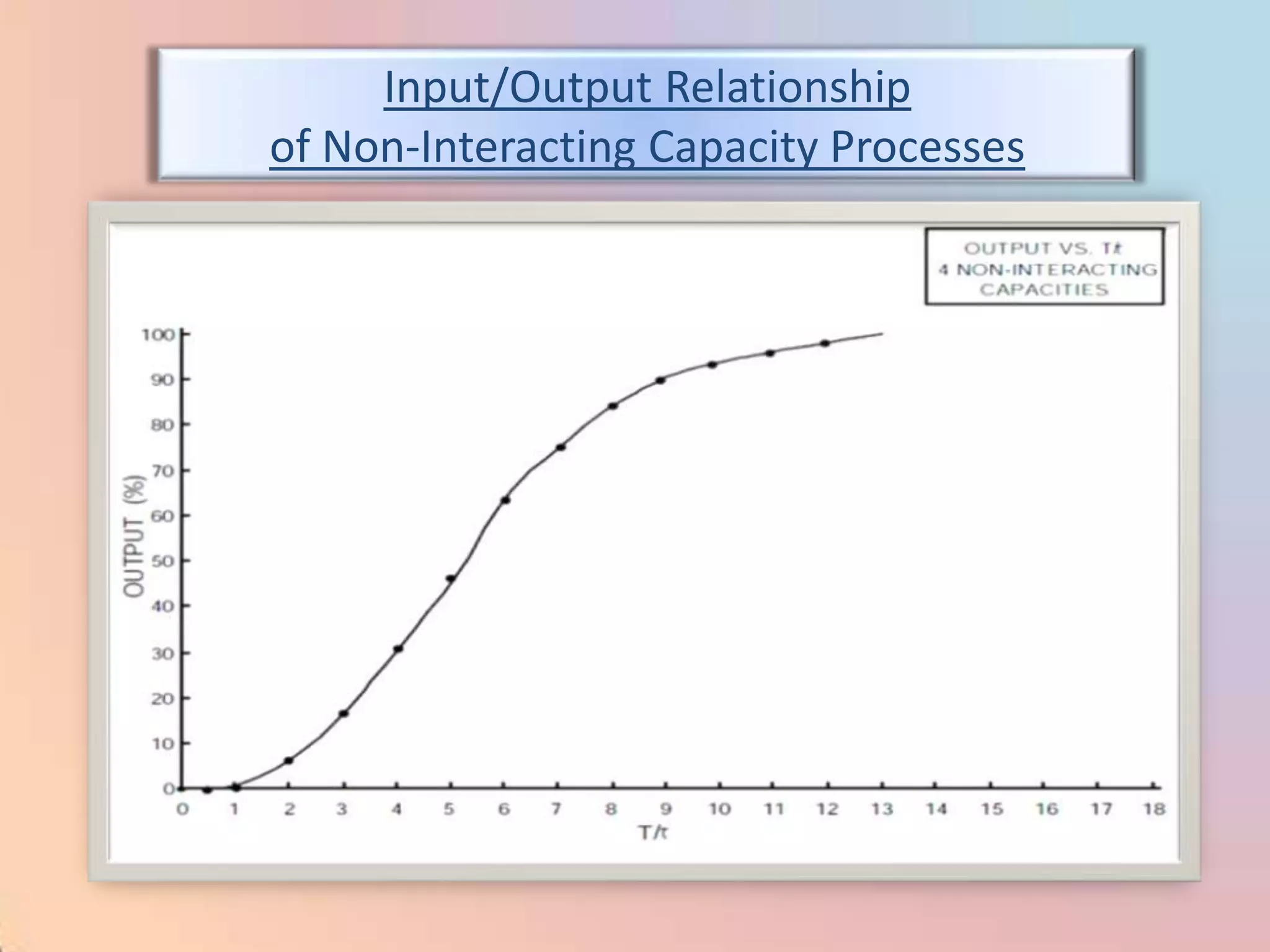
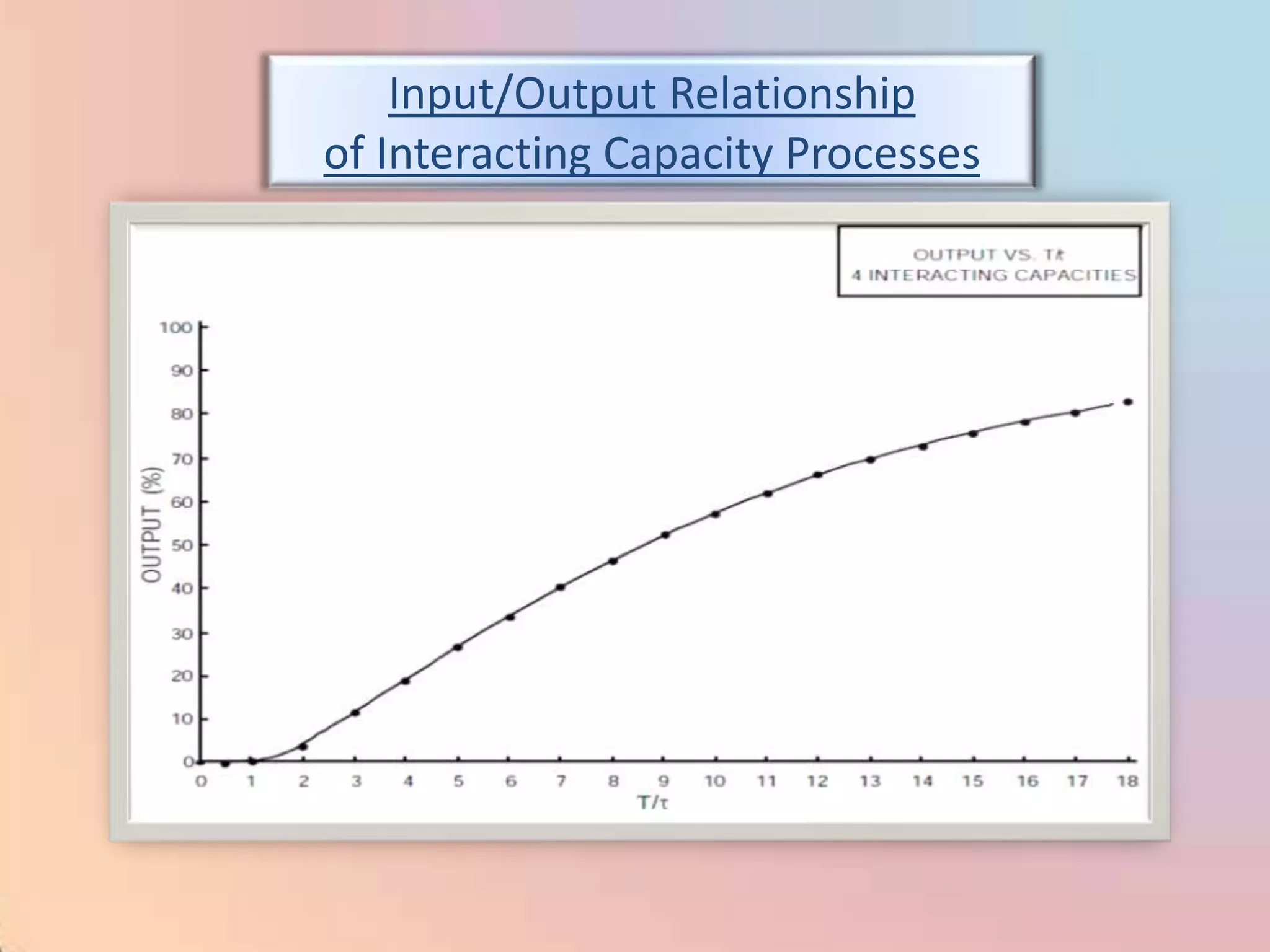



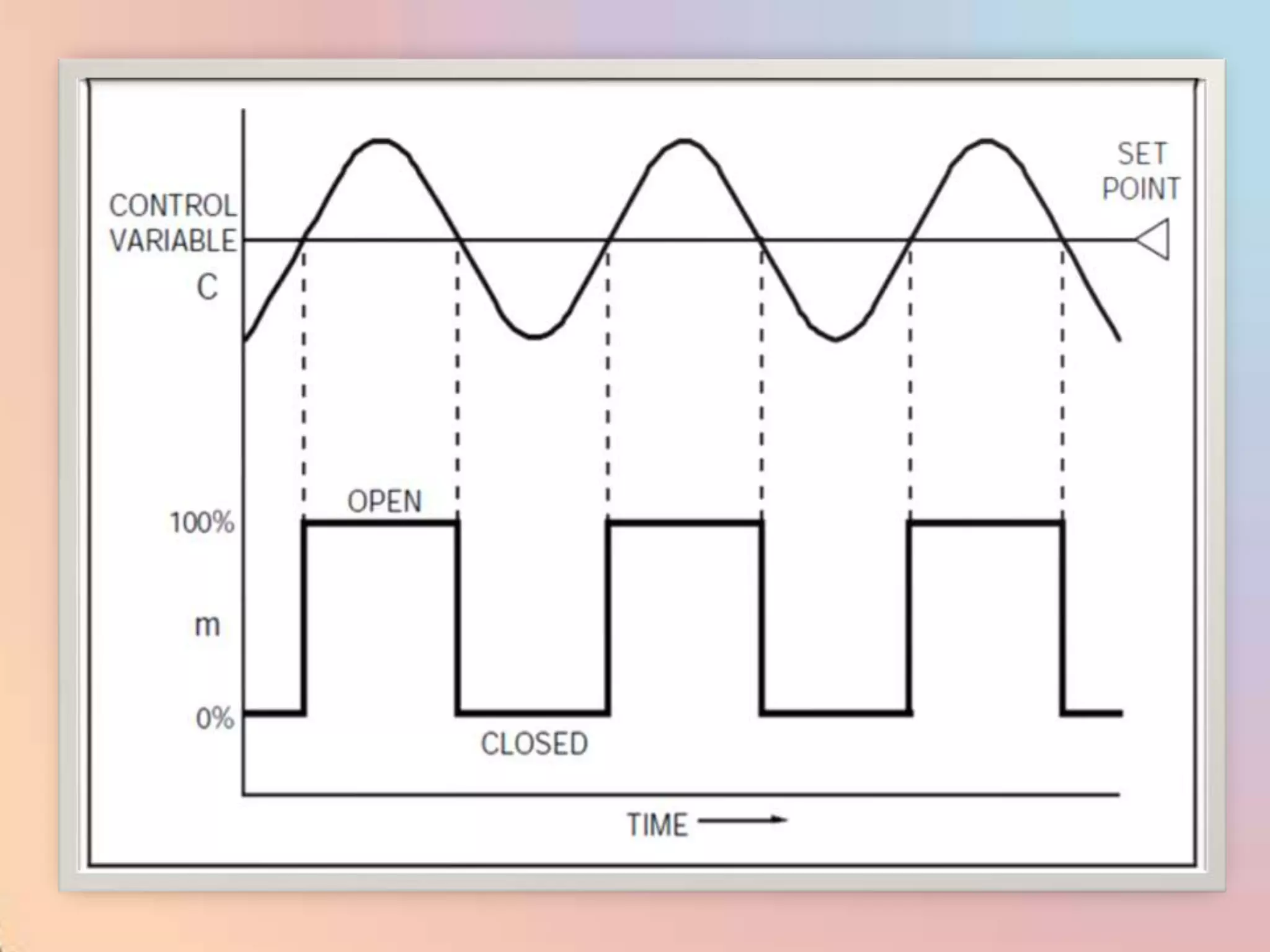












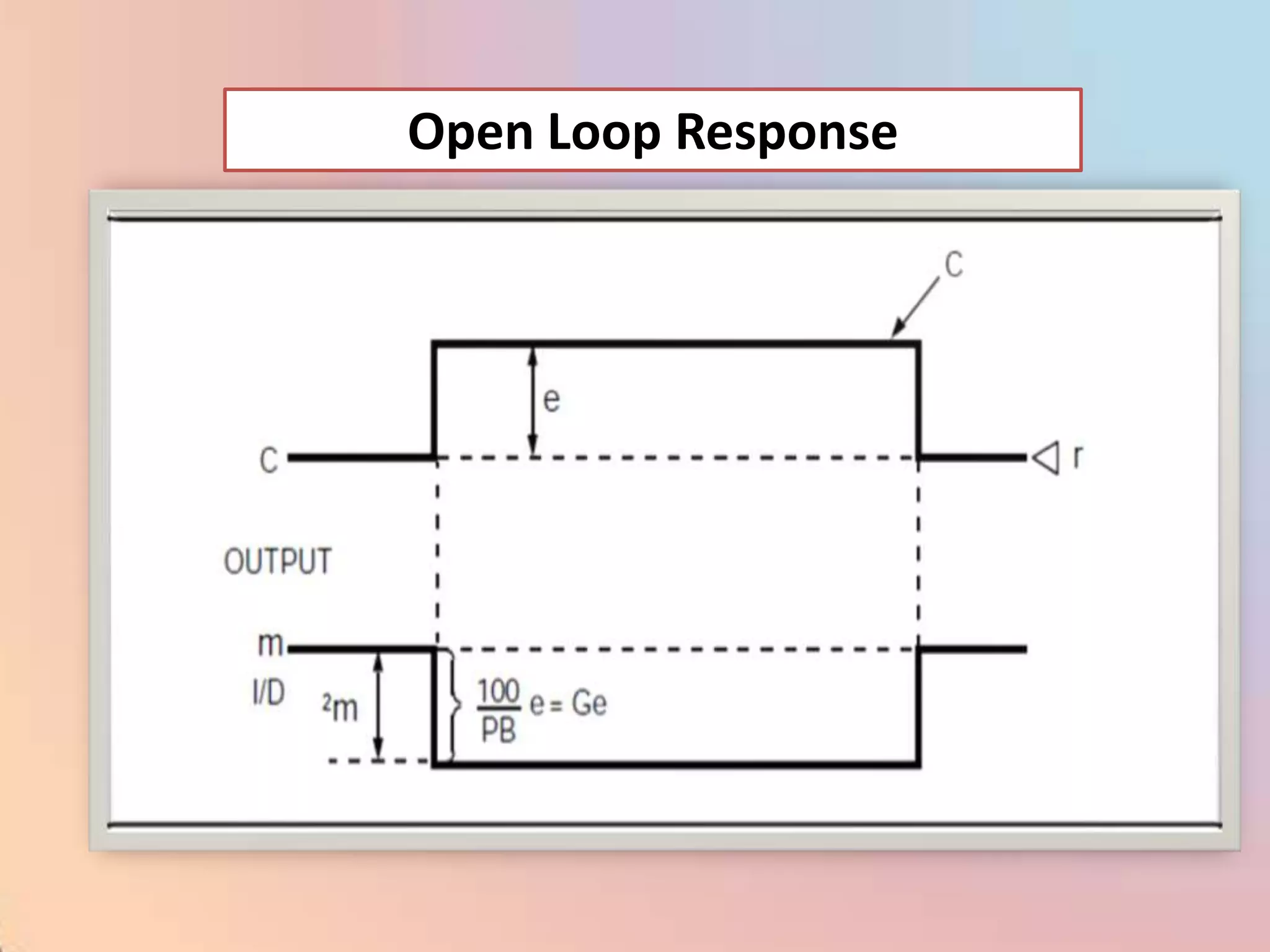

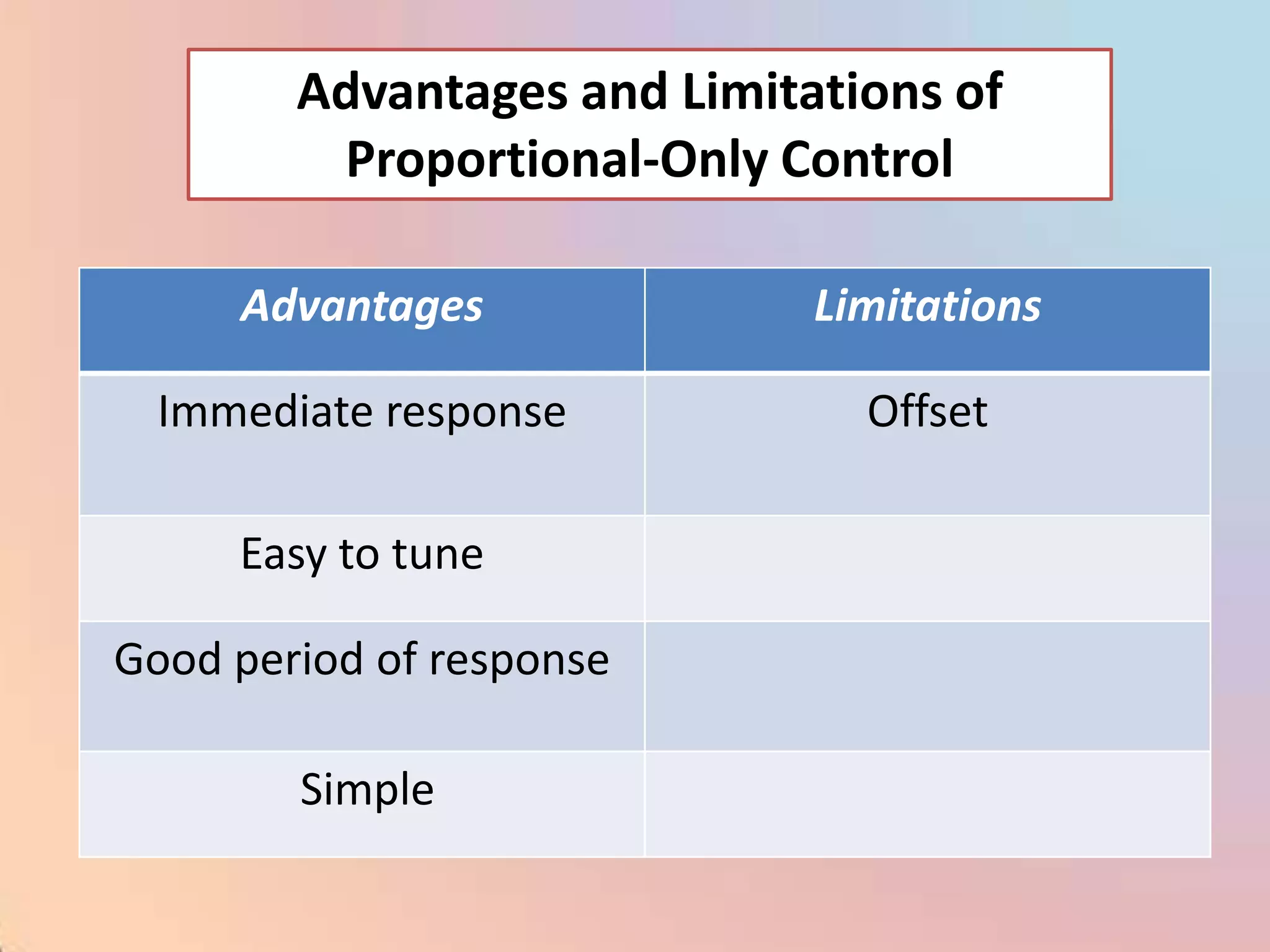


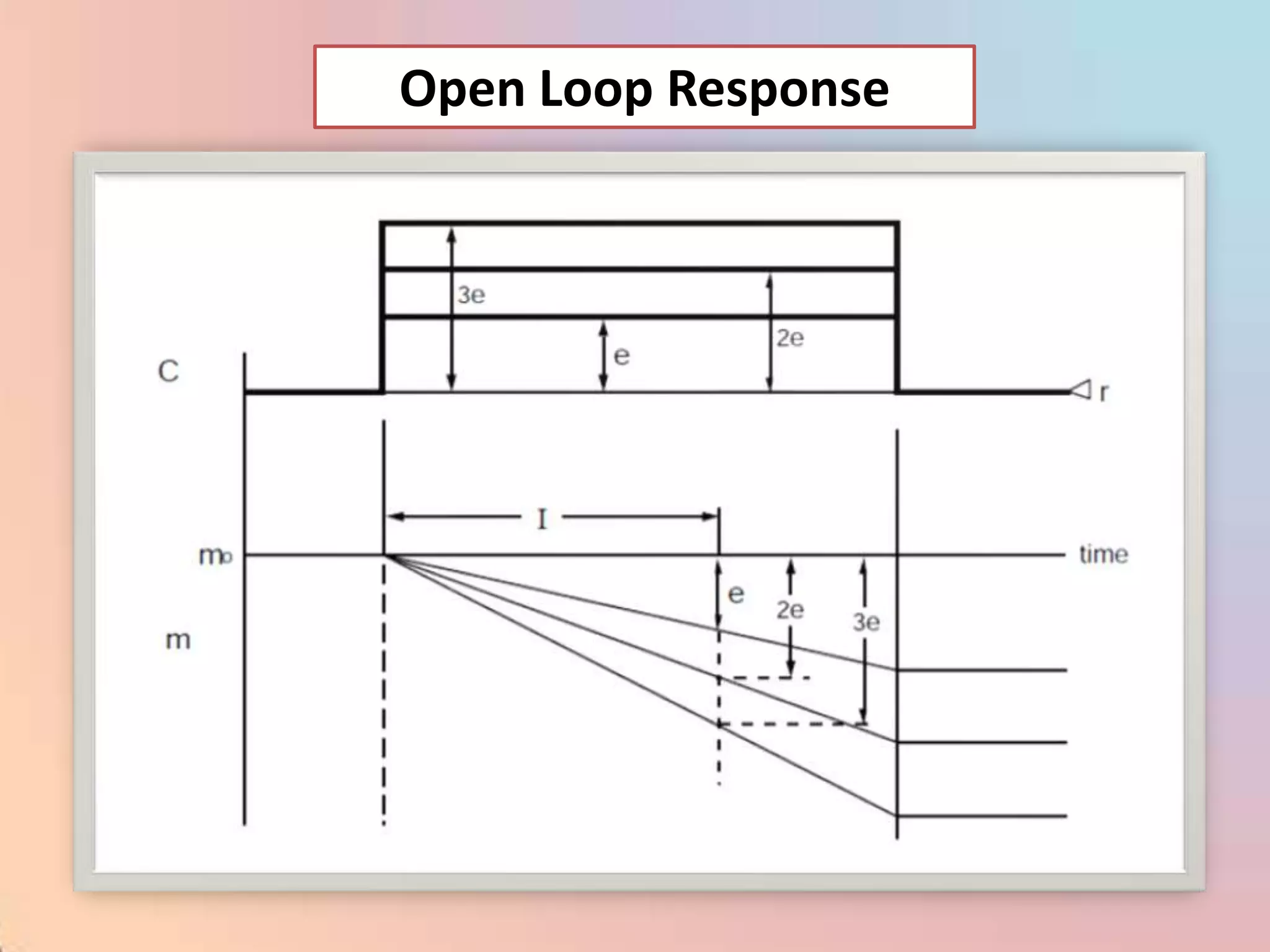
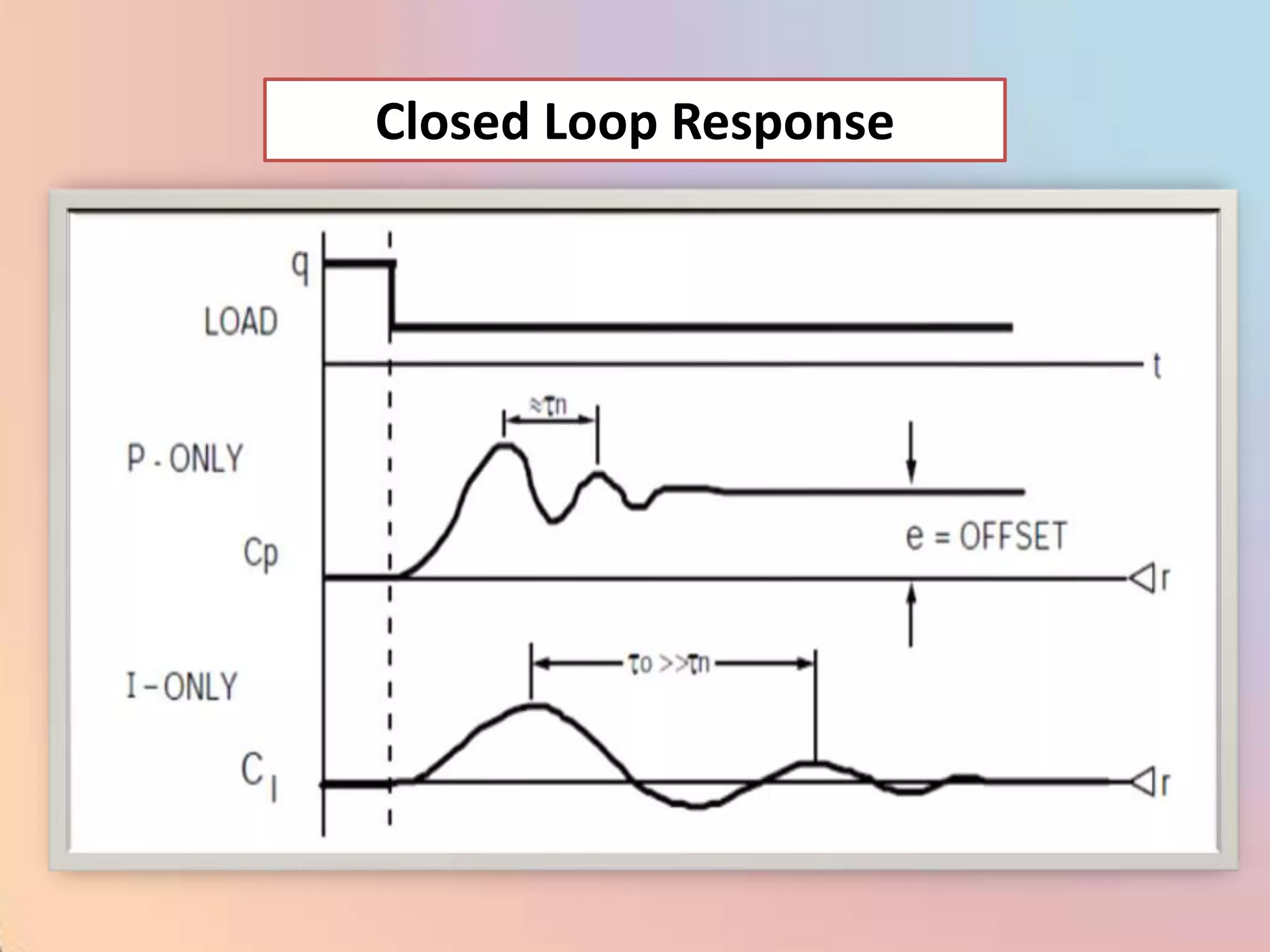


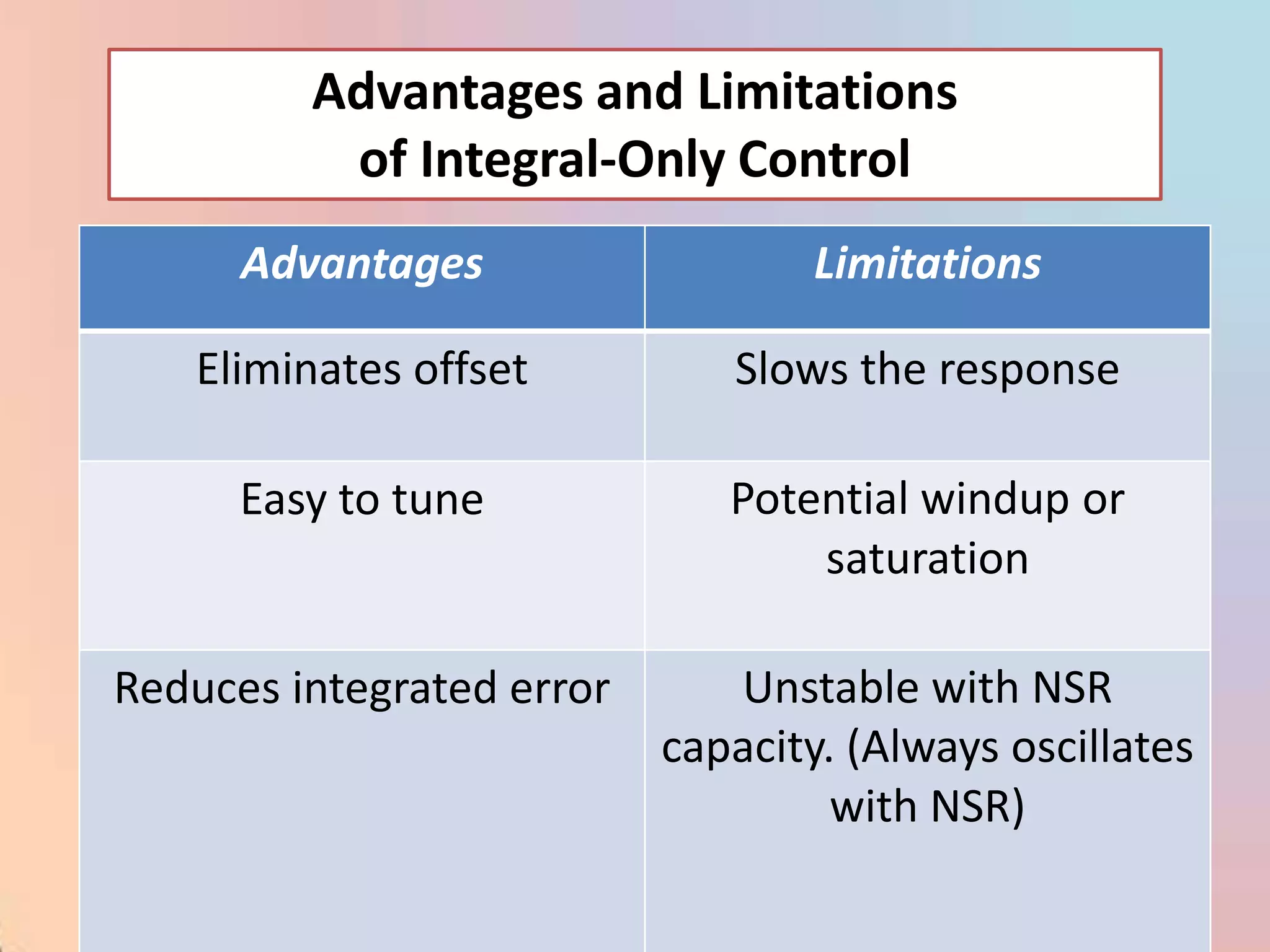



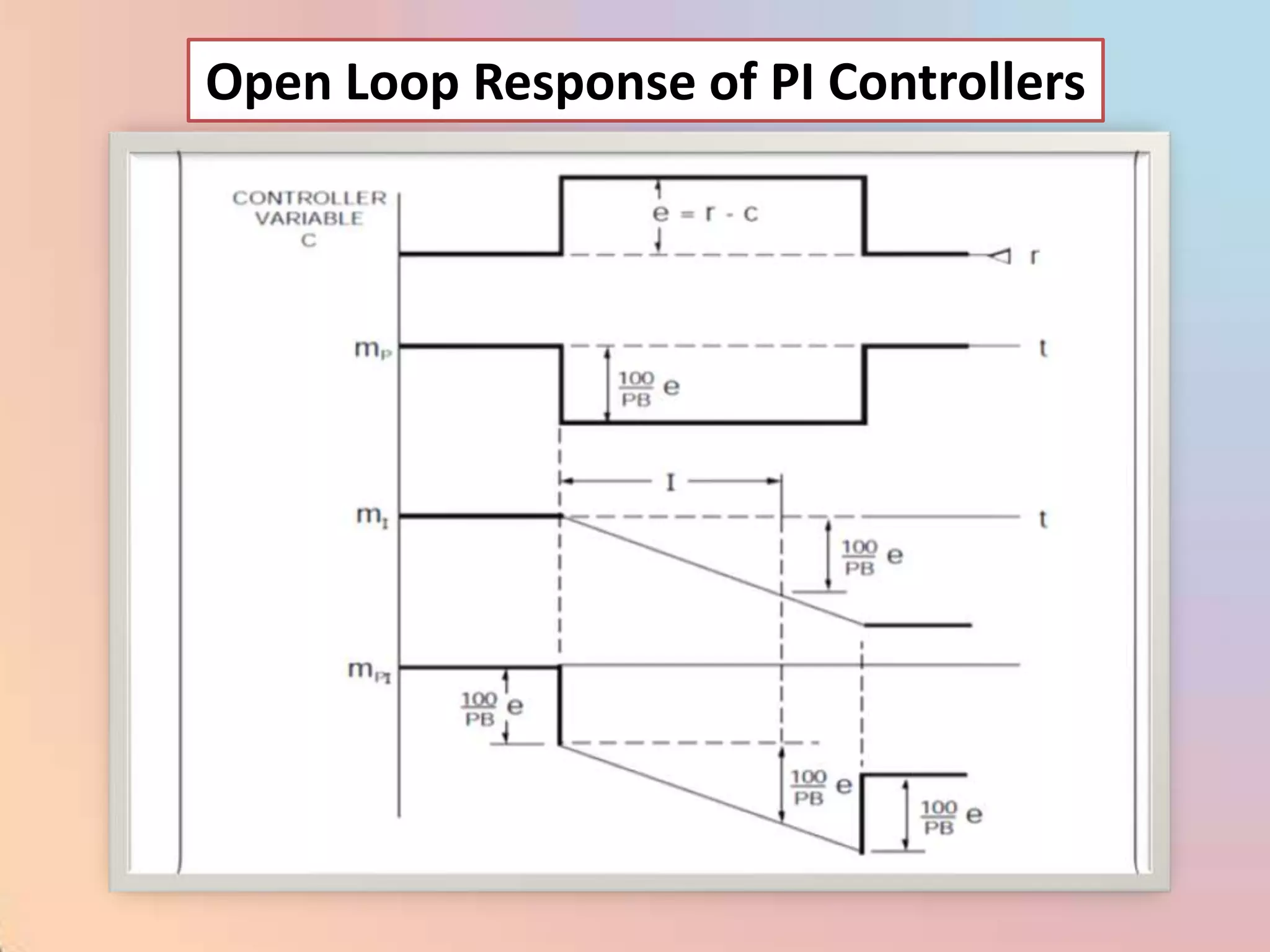
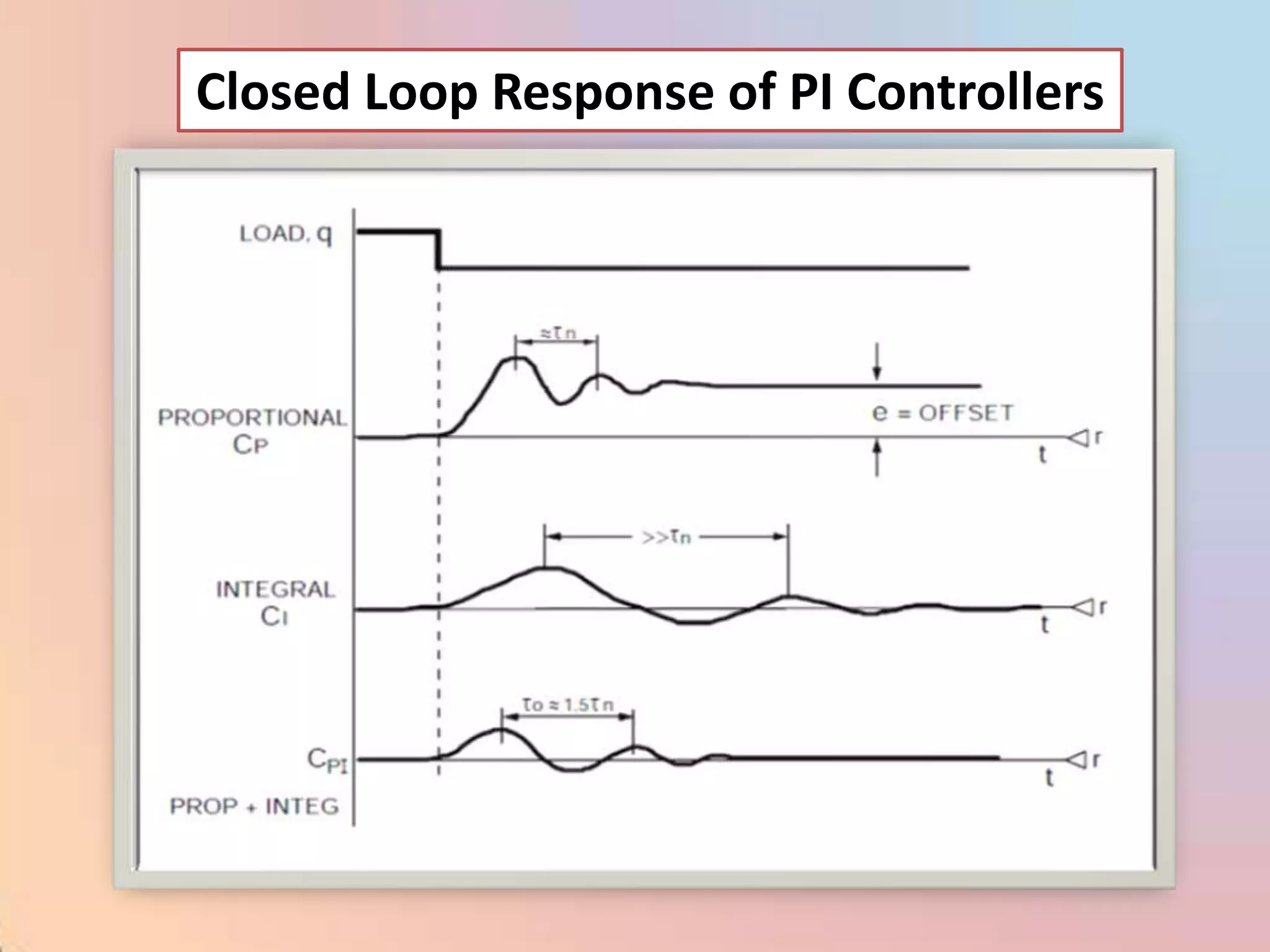
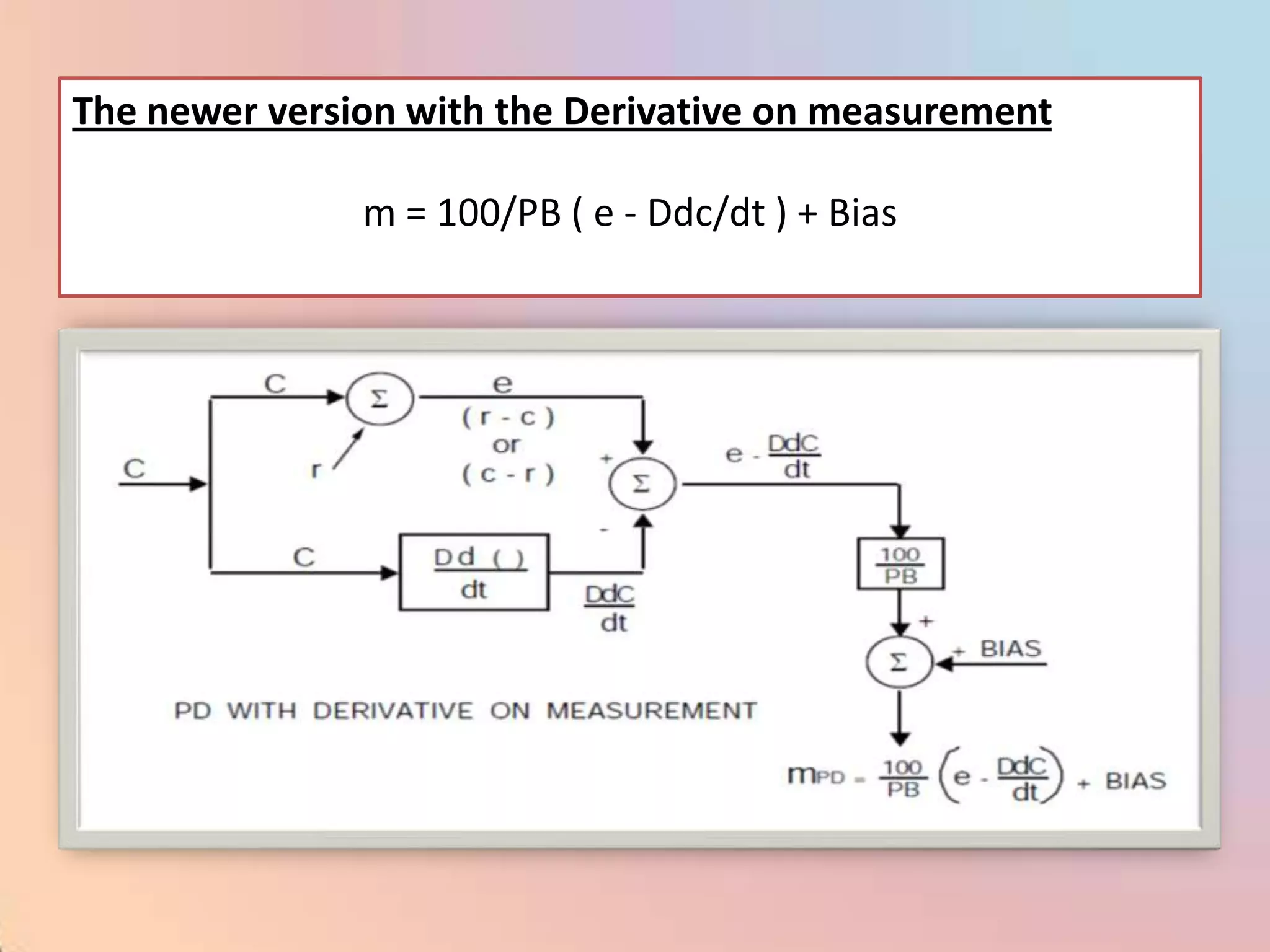
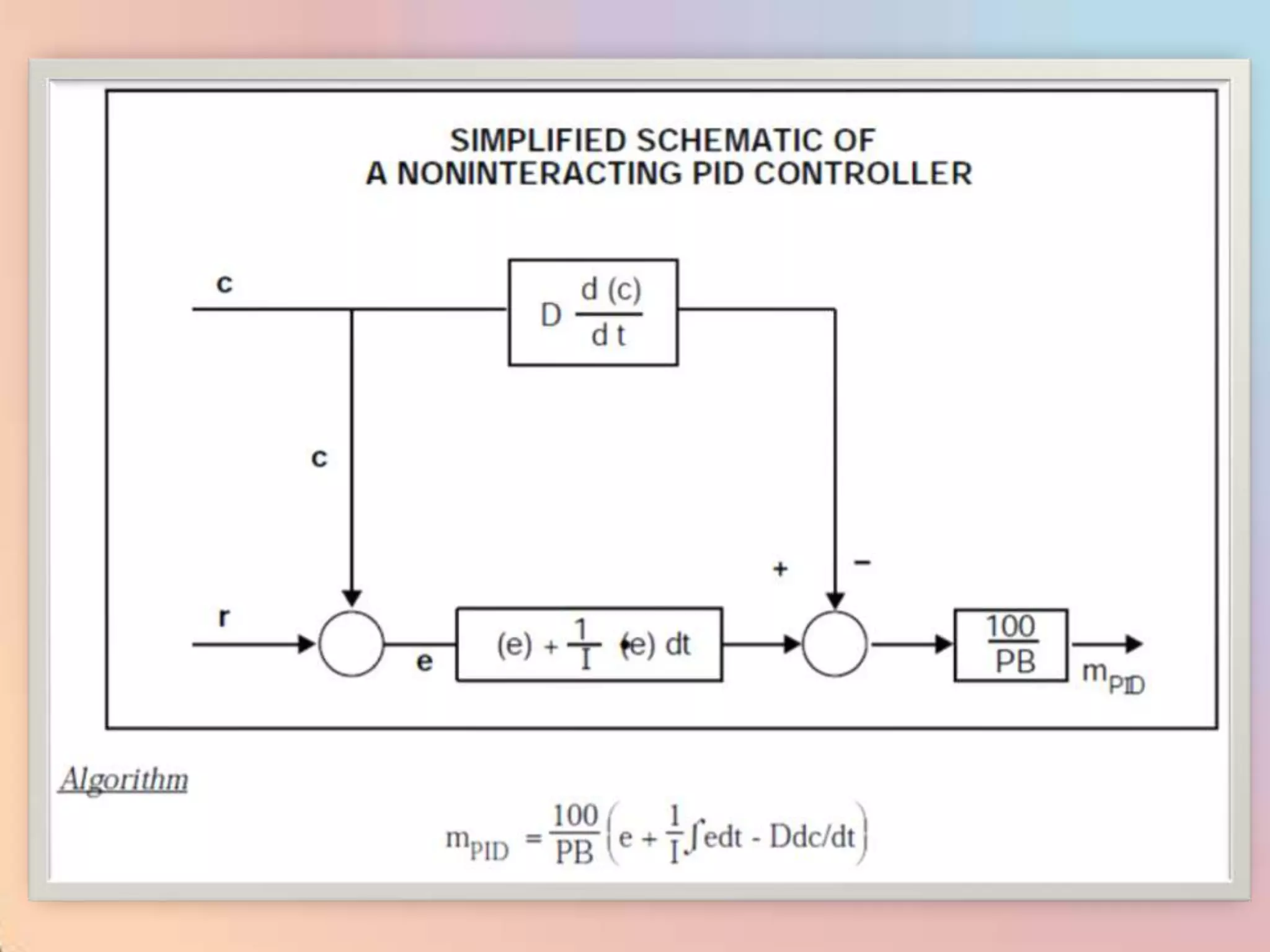
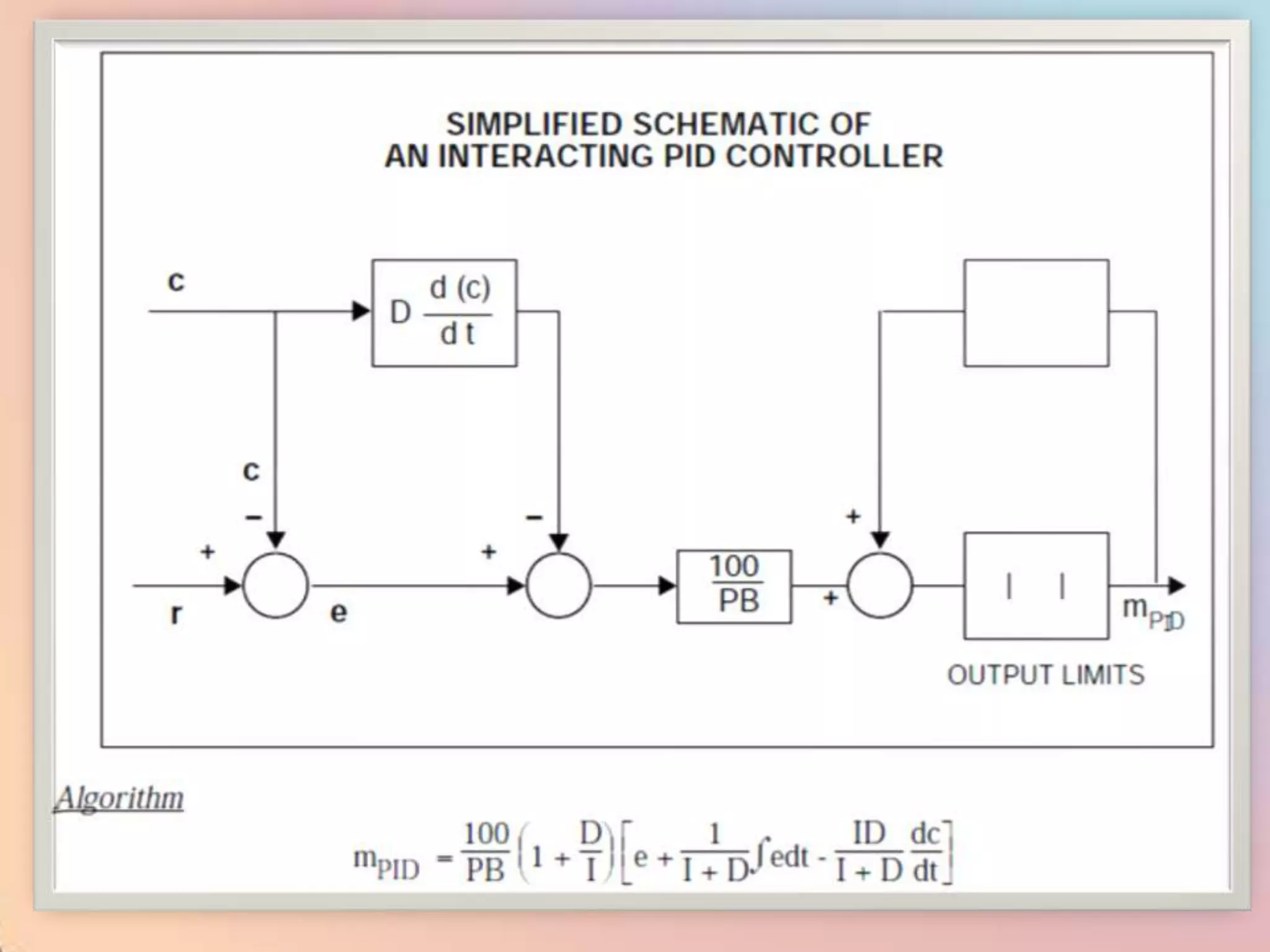
![m = (100/PB) [e + (1/I) edt]](https://image.slidesharecdn.com/industrialprocesscontrol-120310035732-phpapp02/75/Industrial-process-control-98-2048.jpg)
















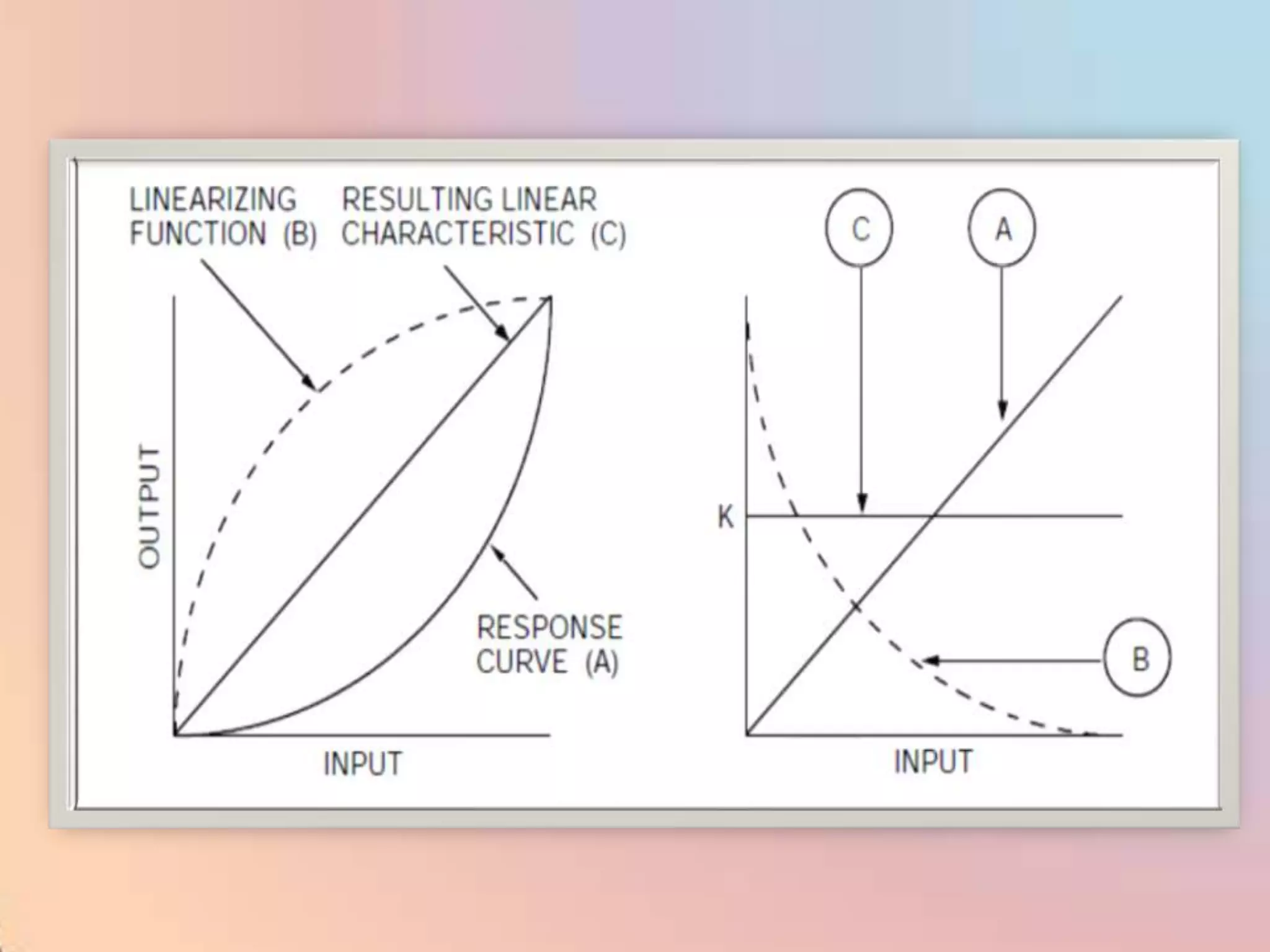
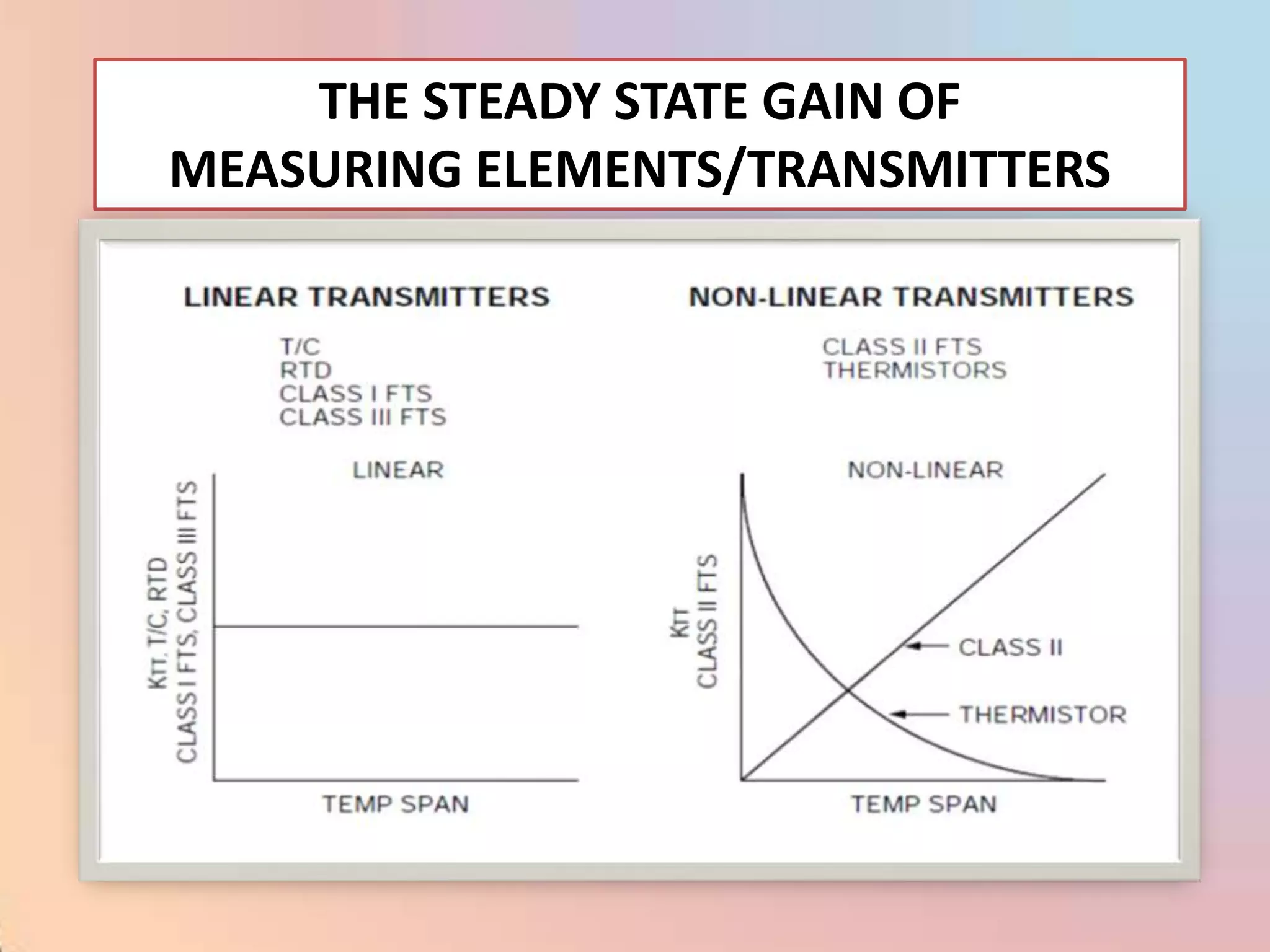

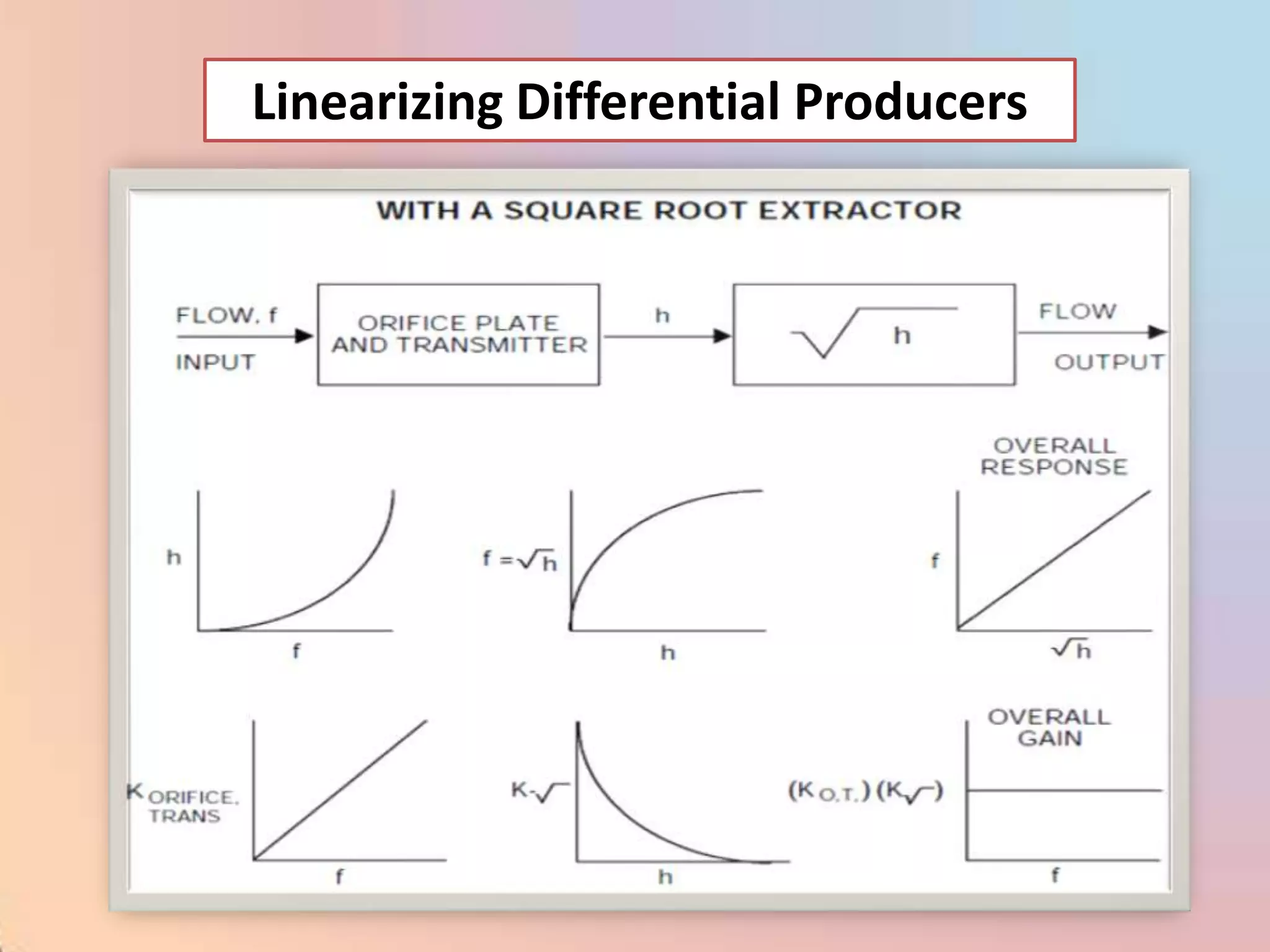

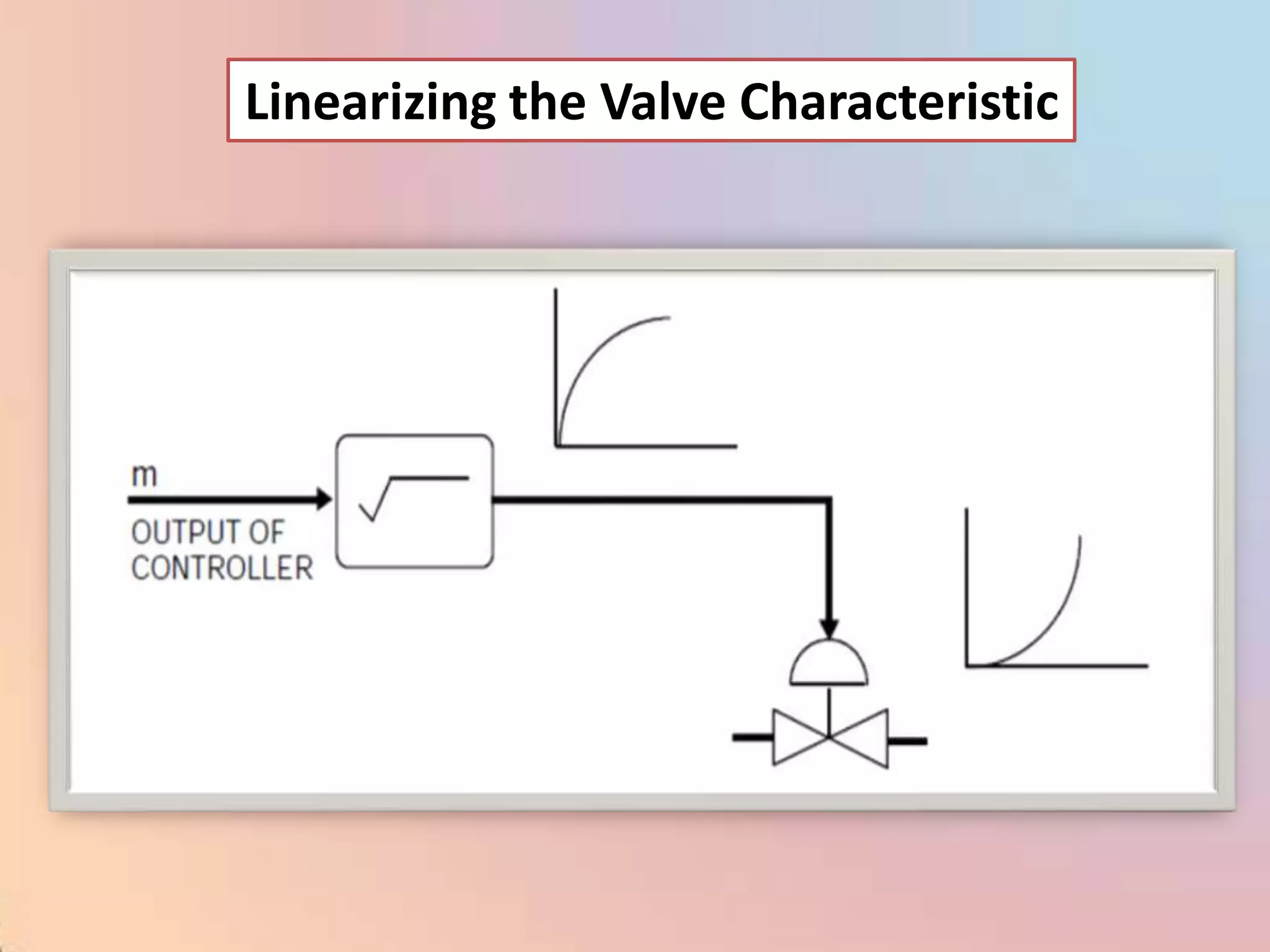
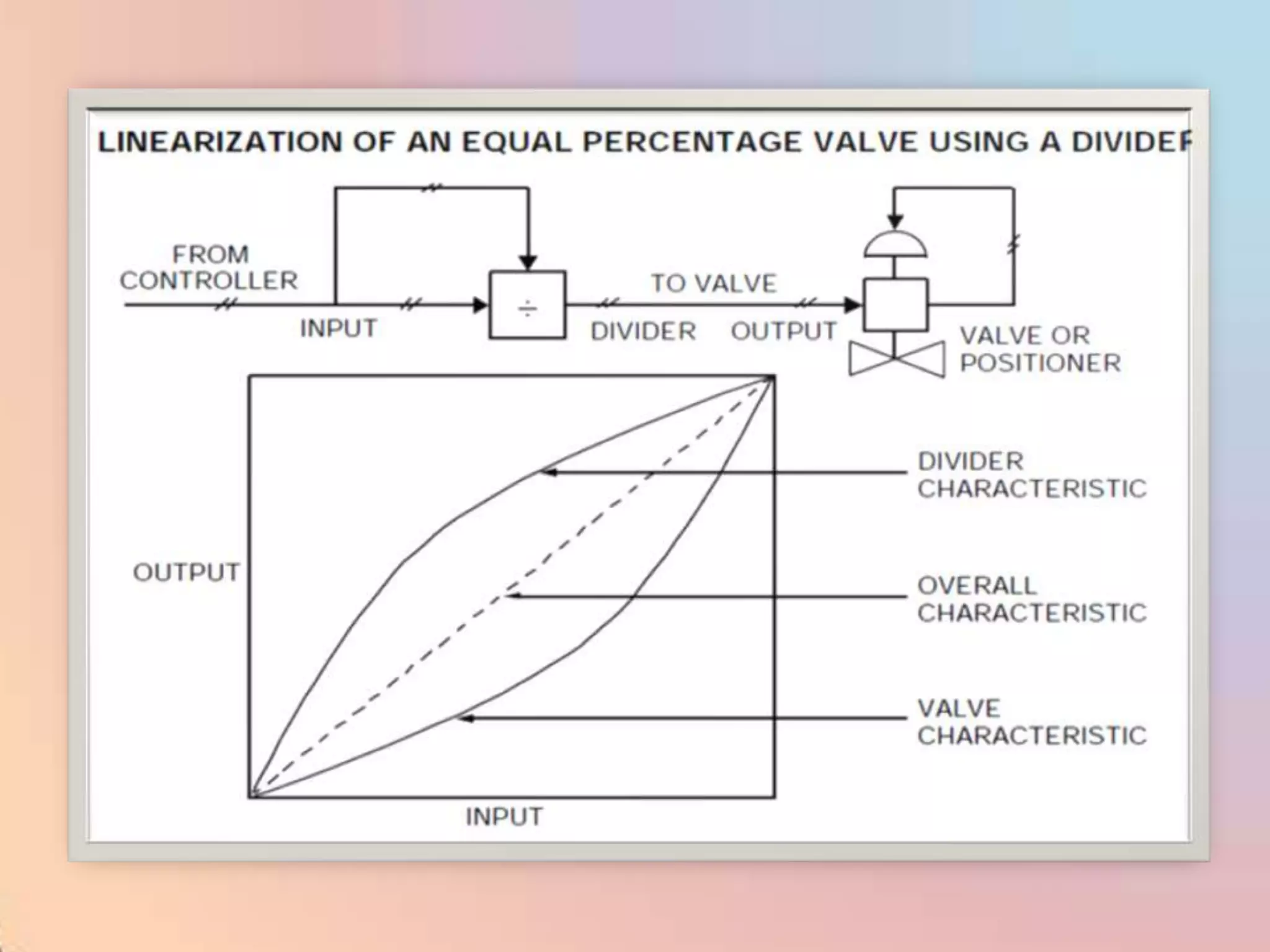

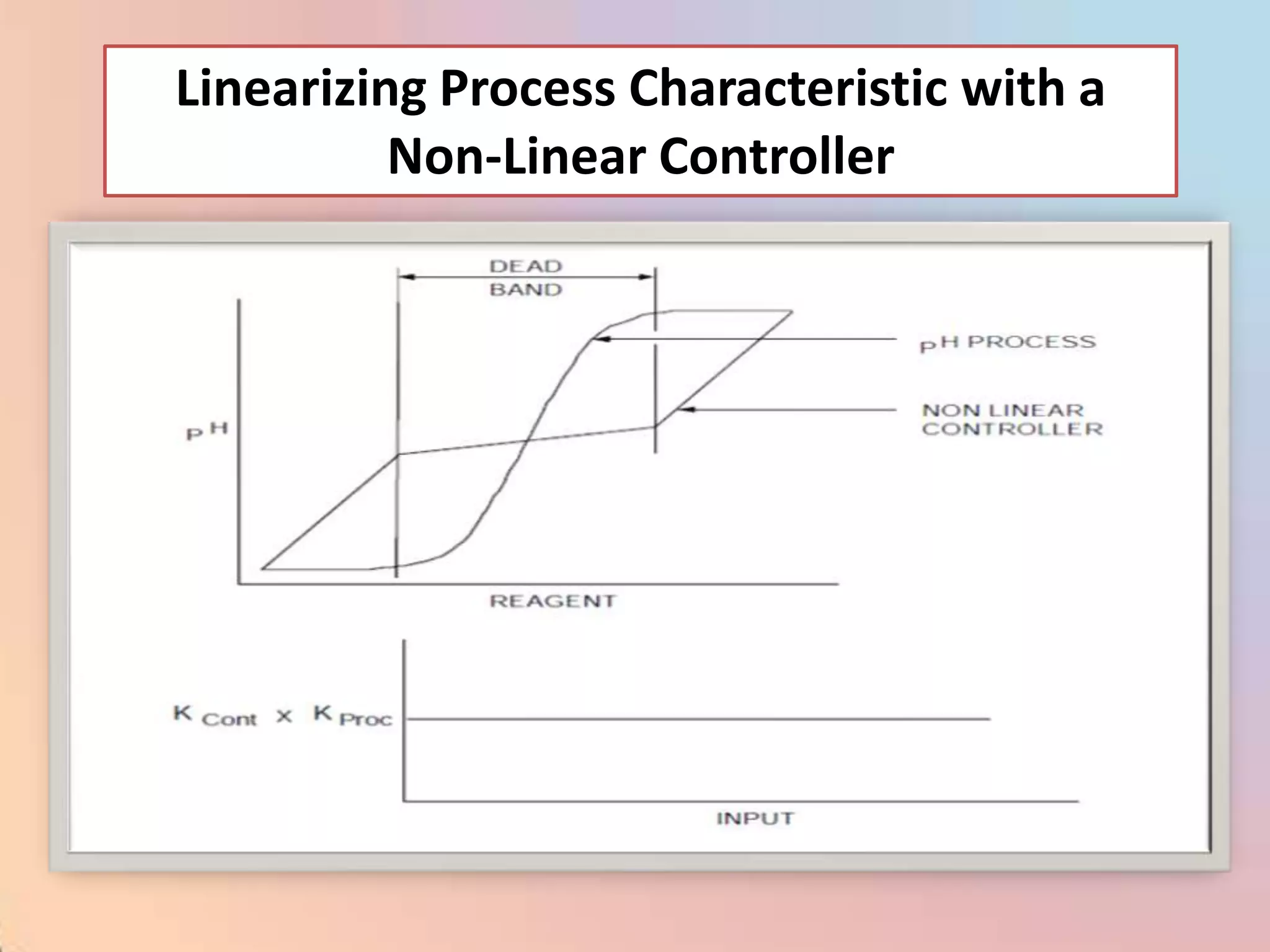
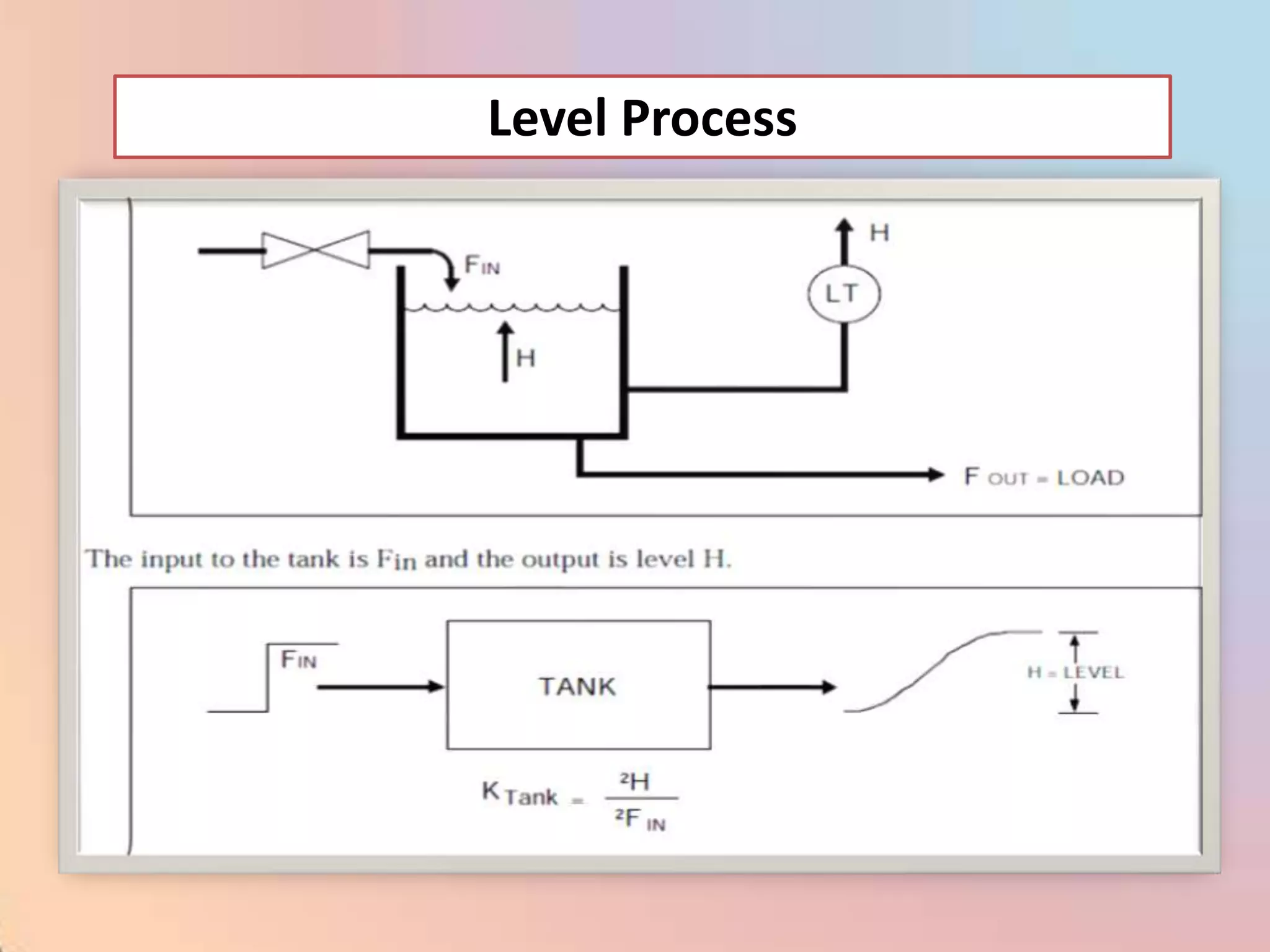
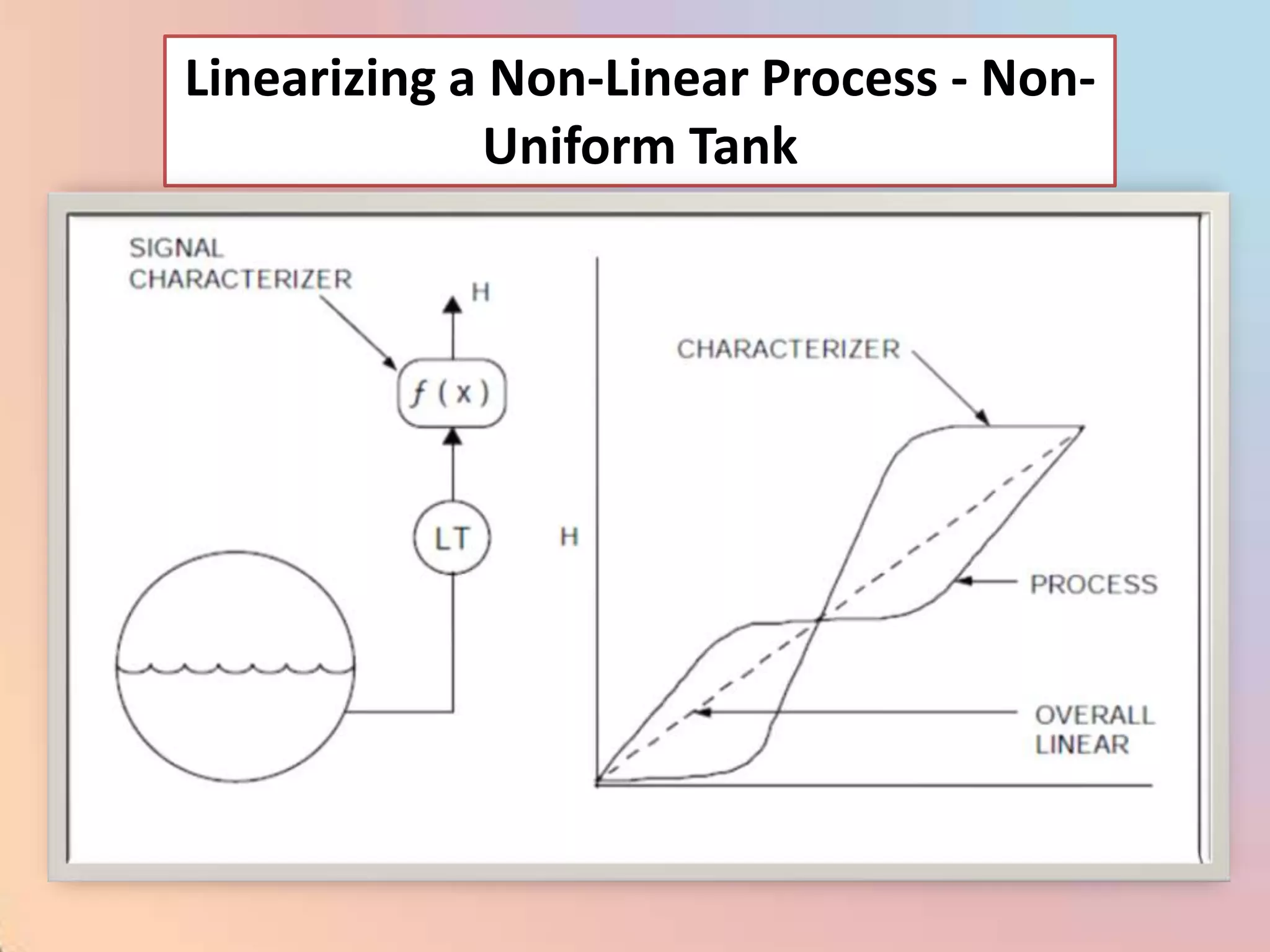
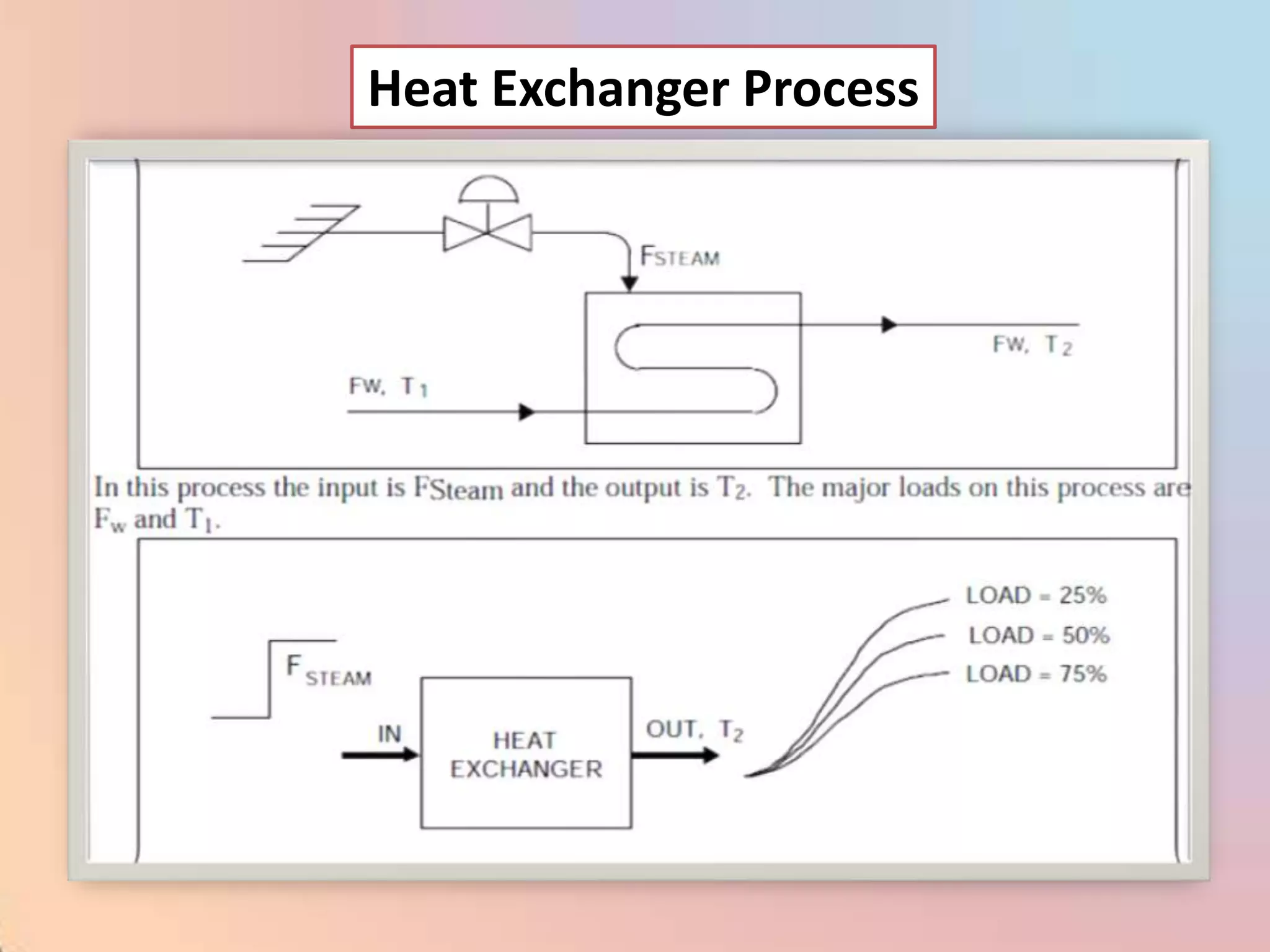
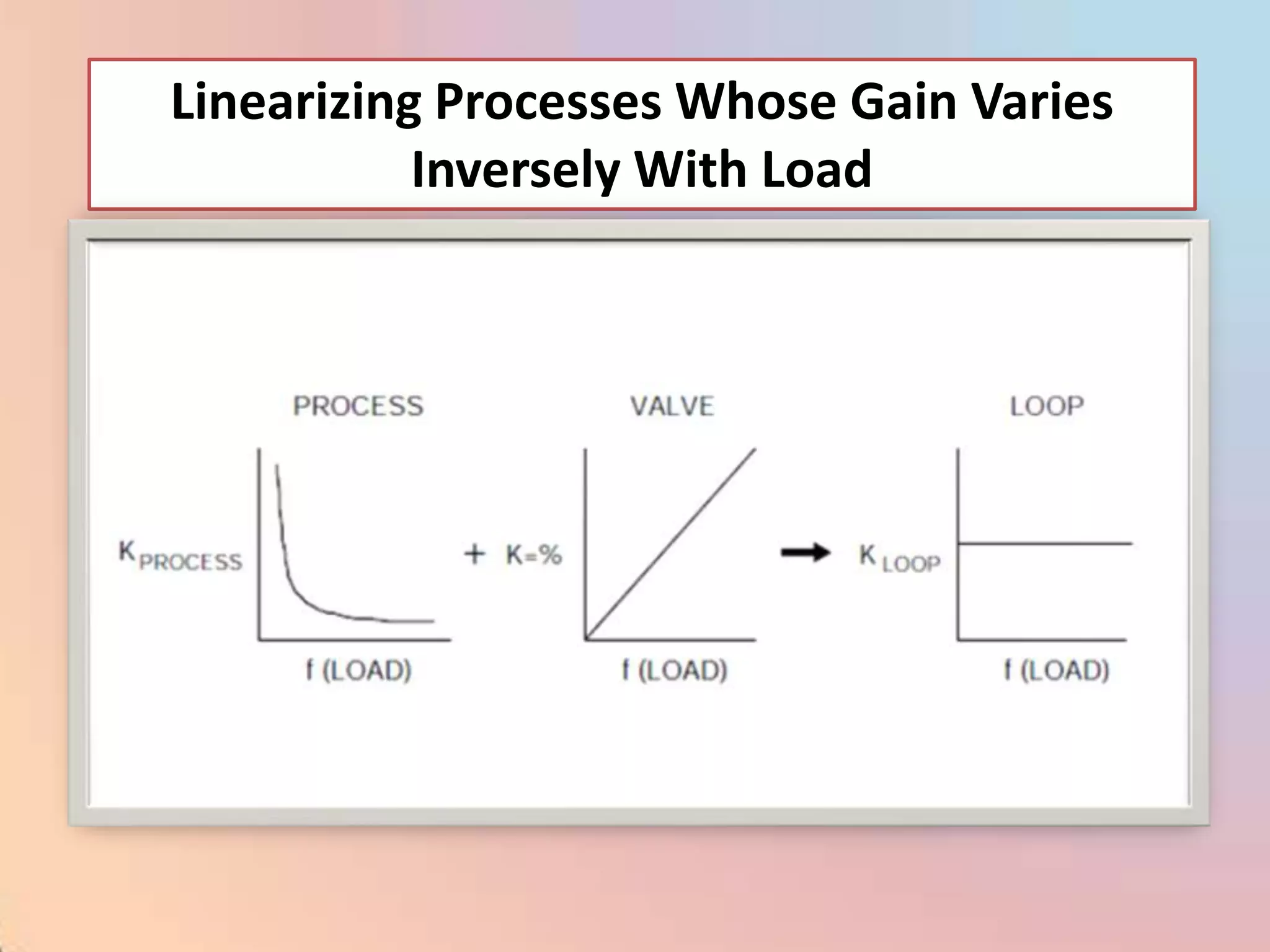

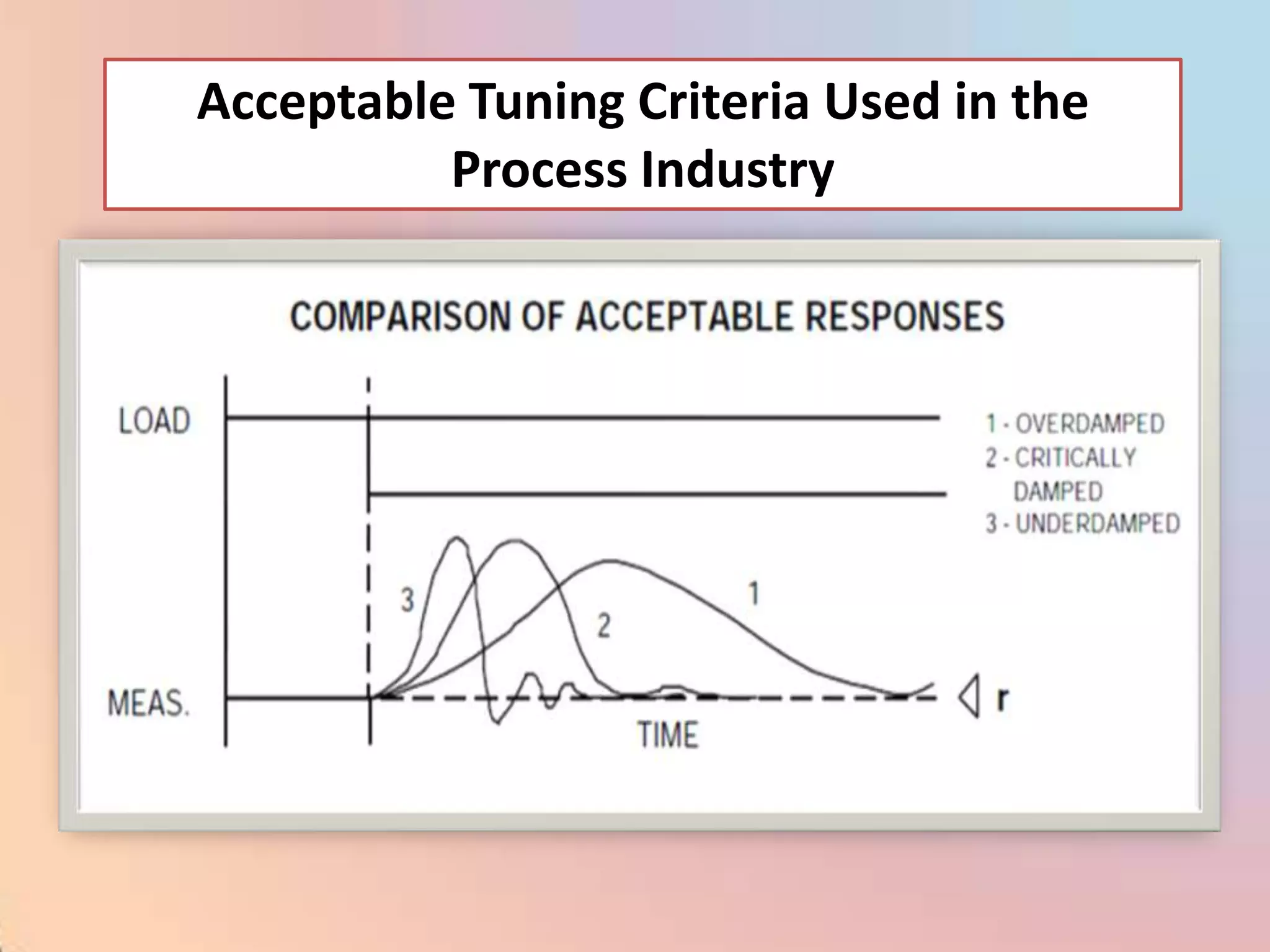








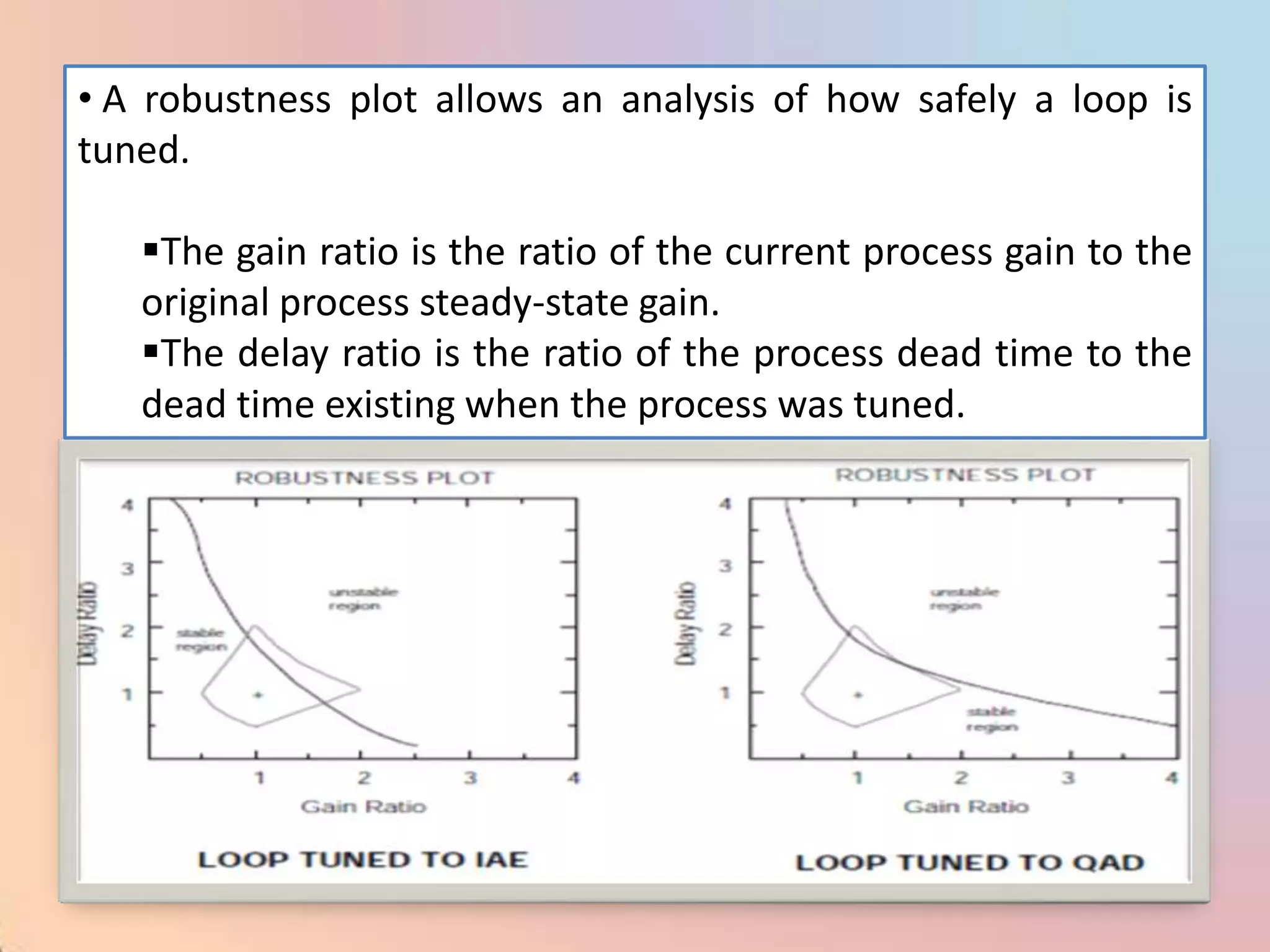








































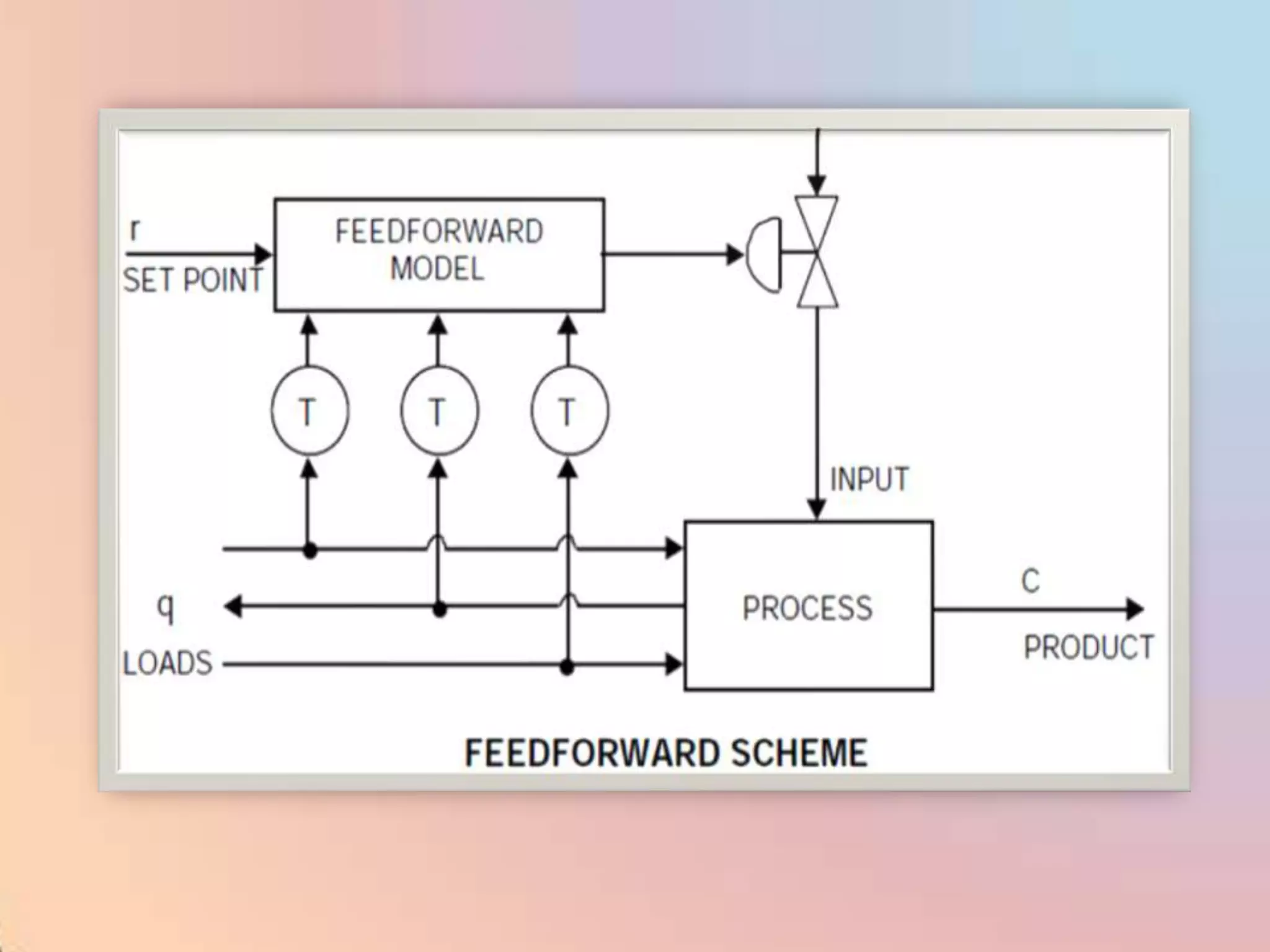



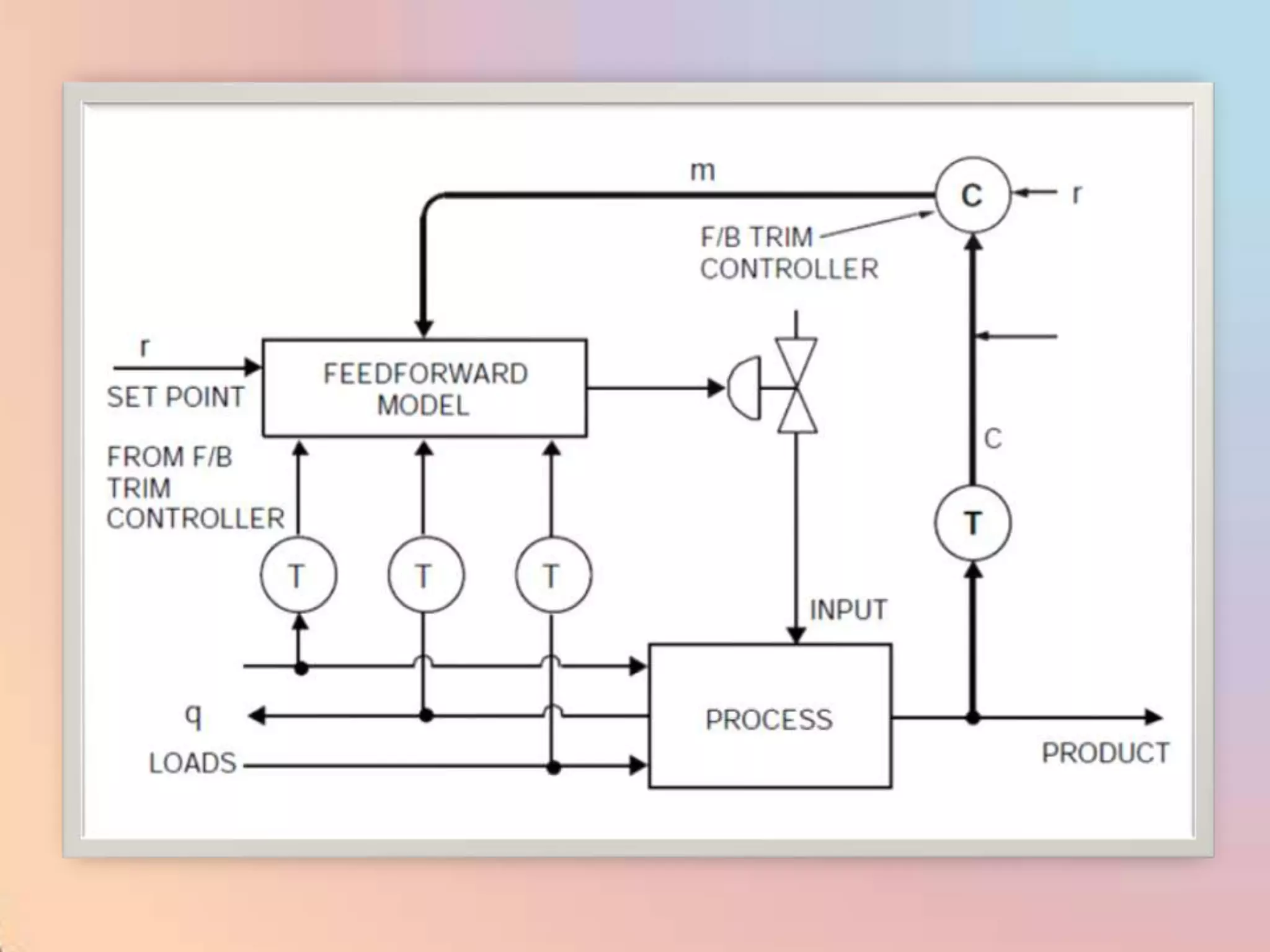
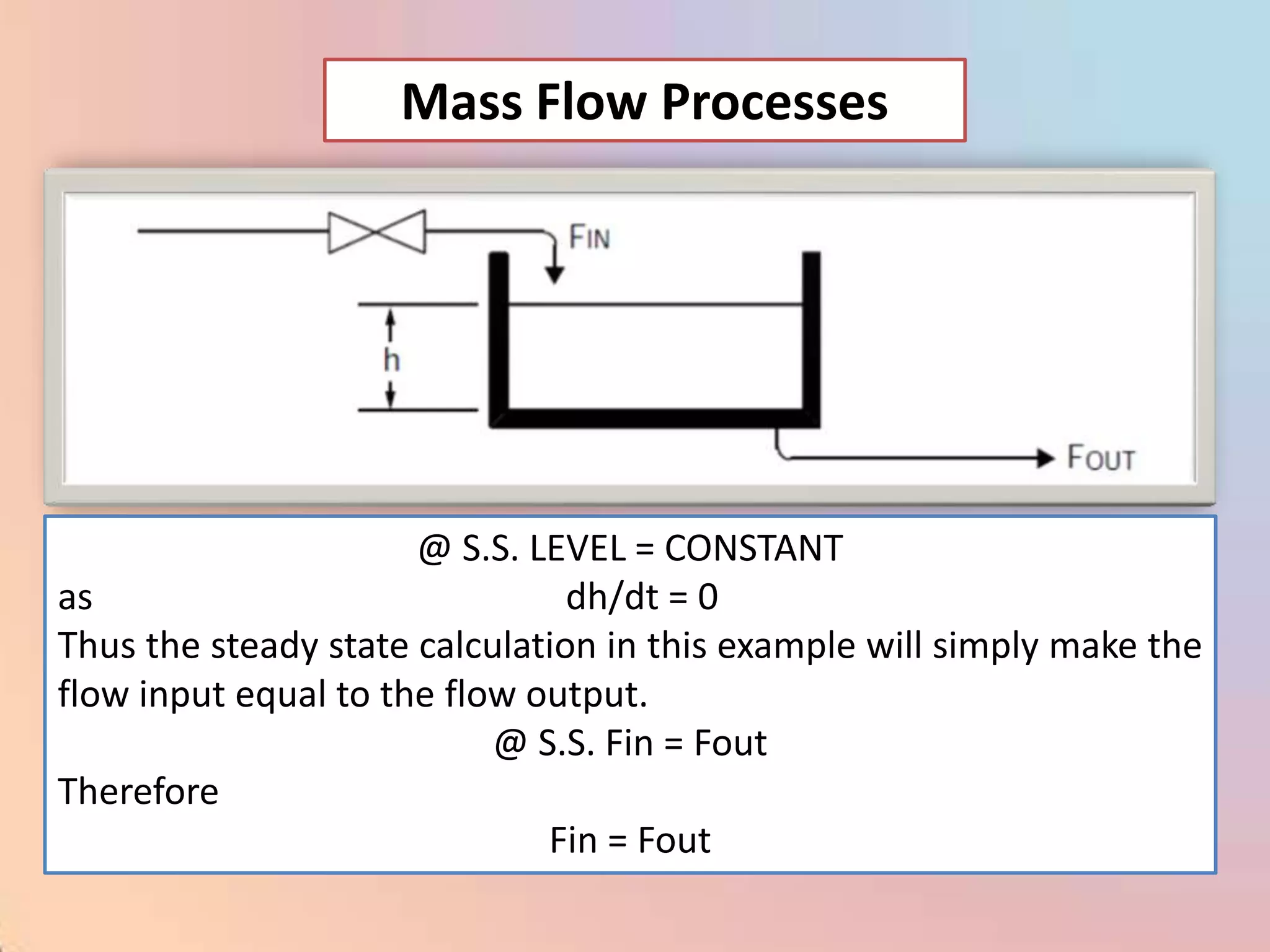

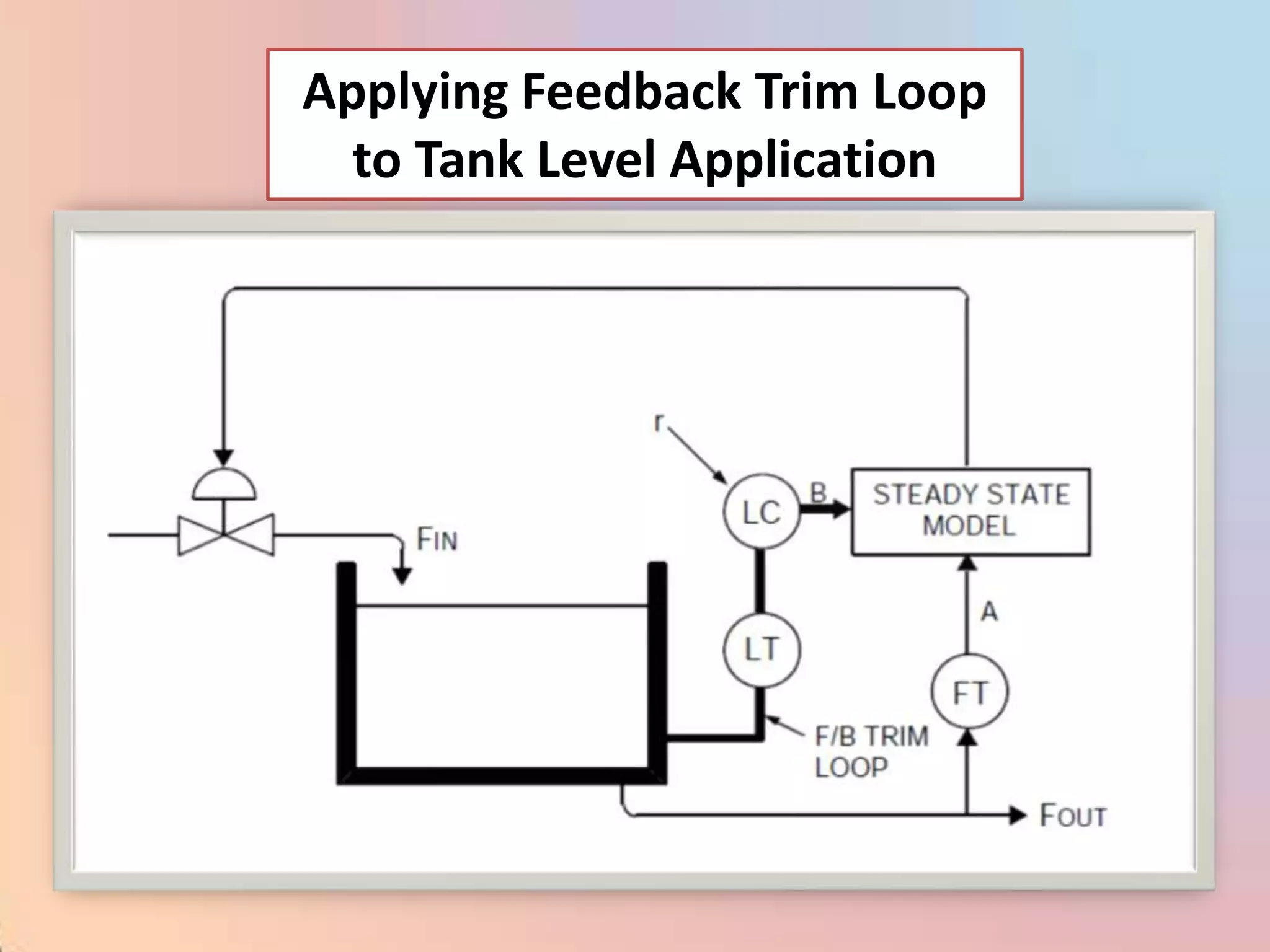















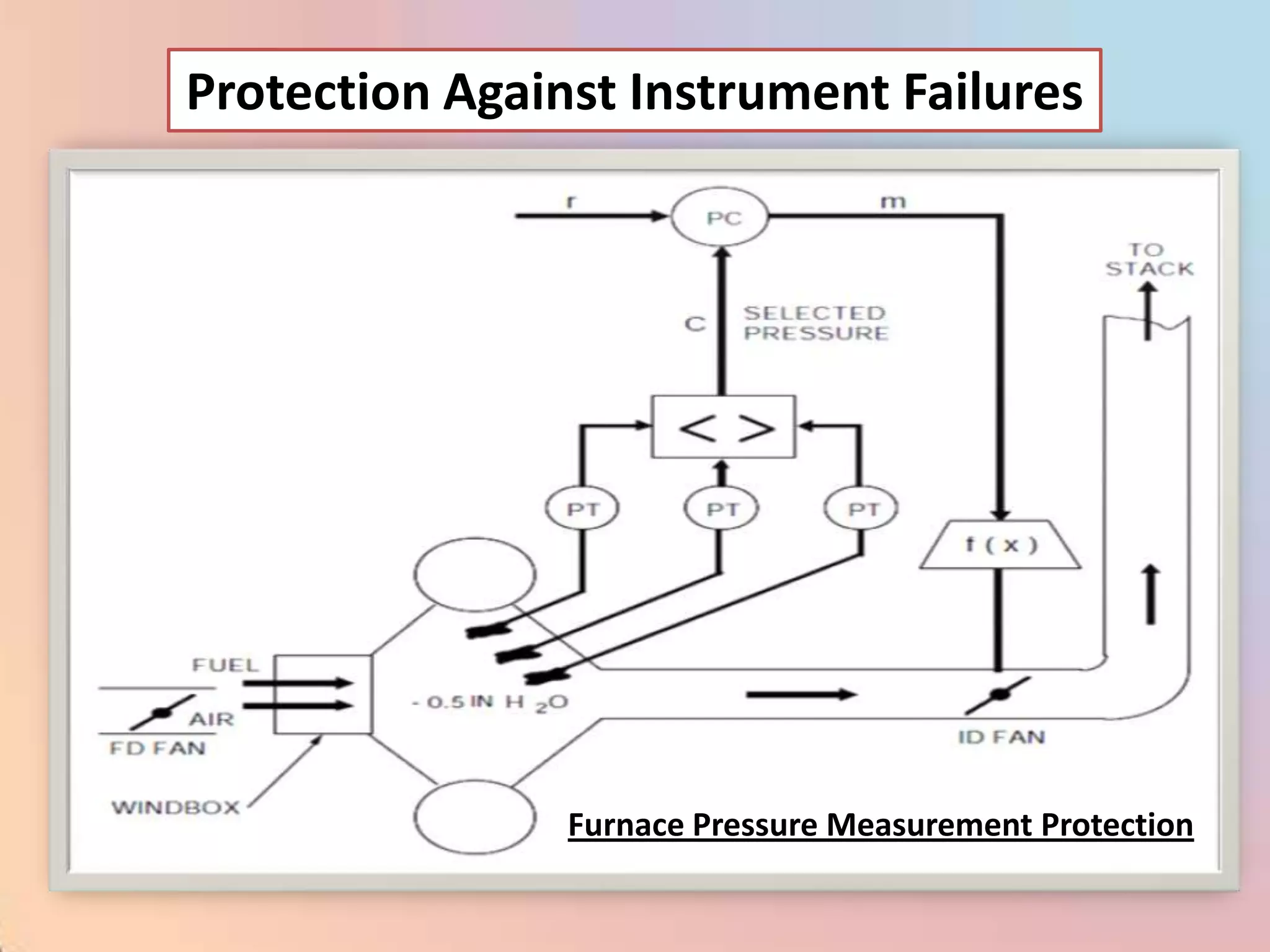
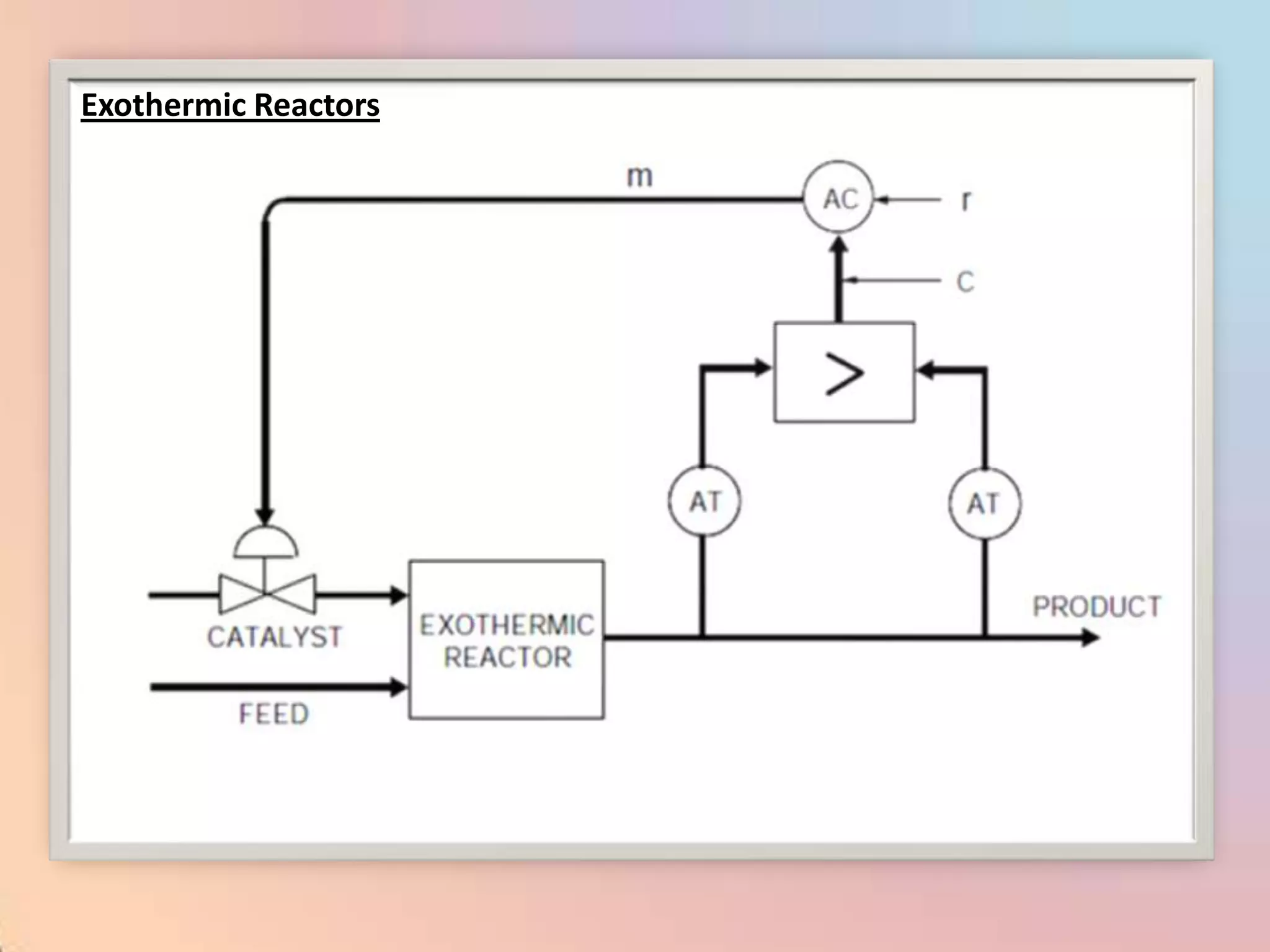
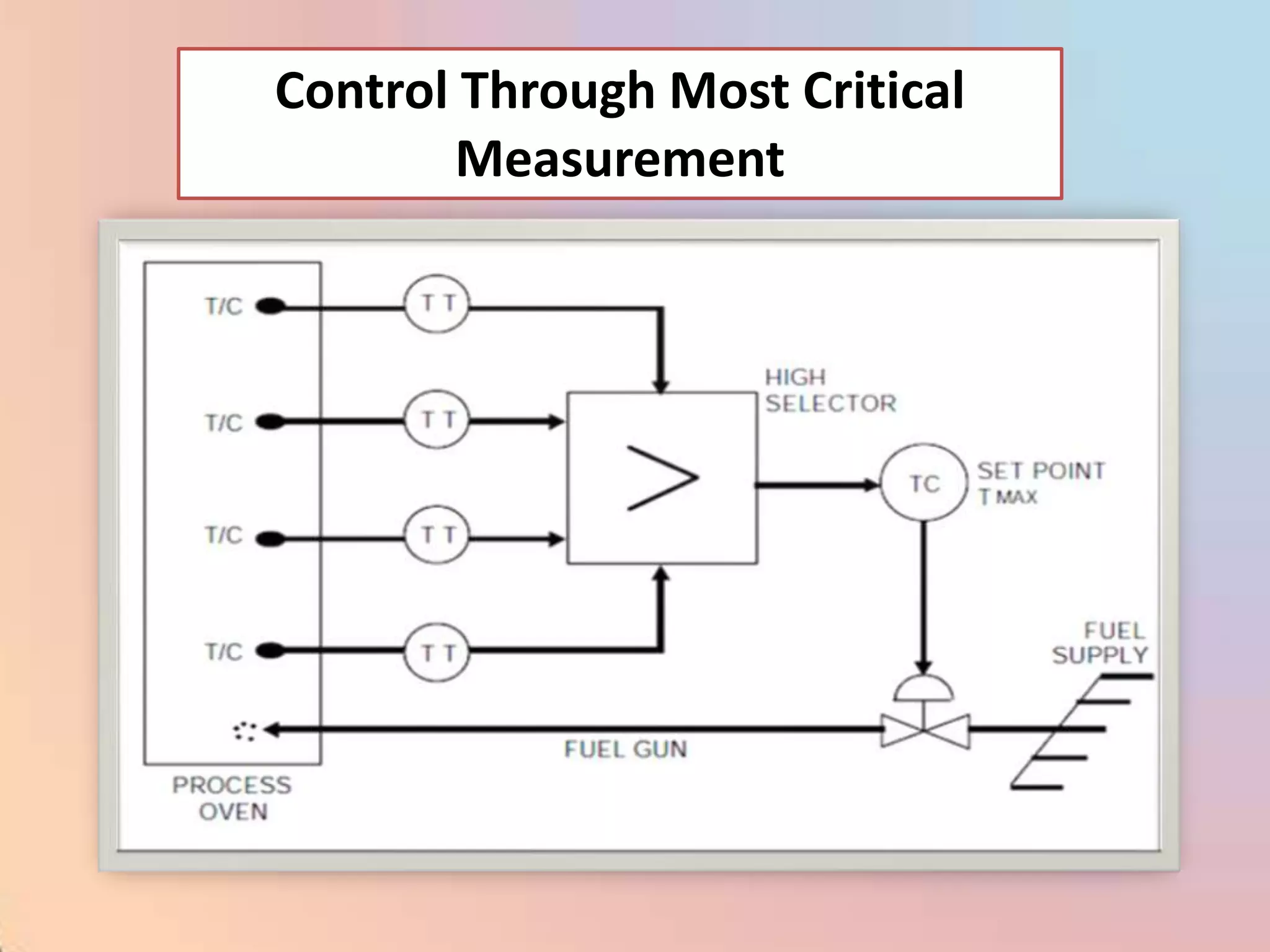

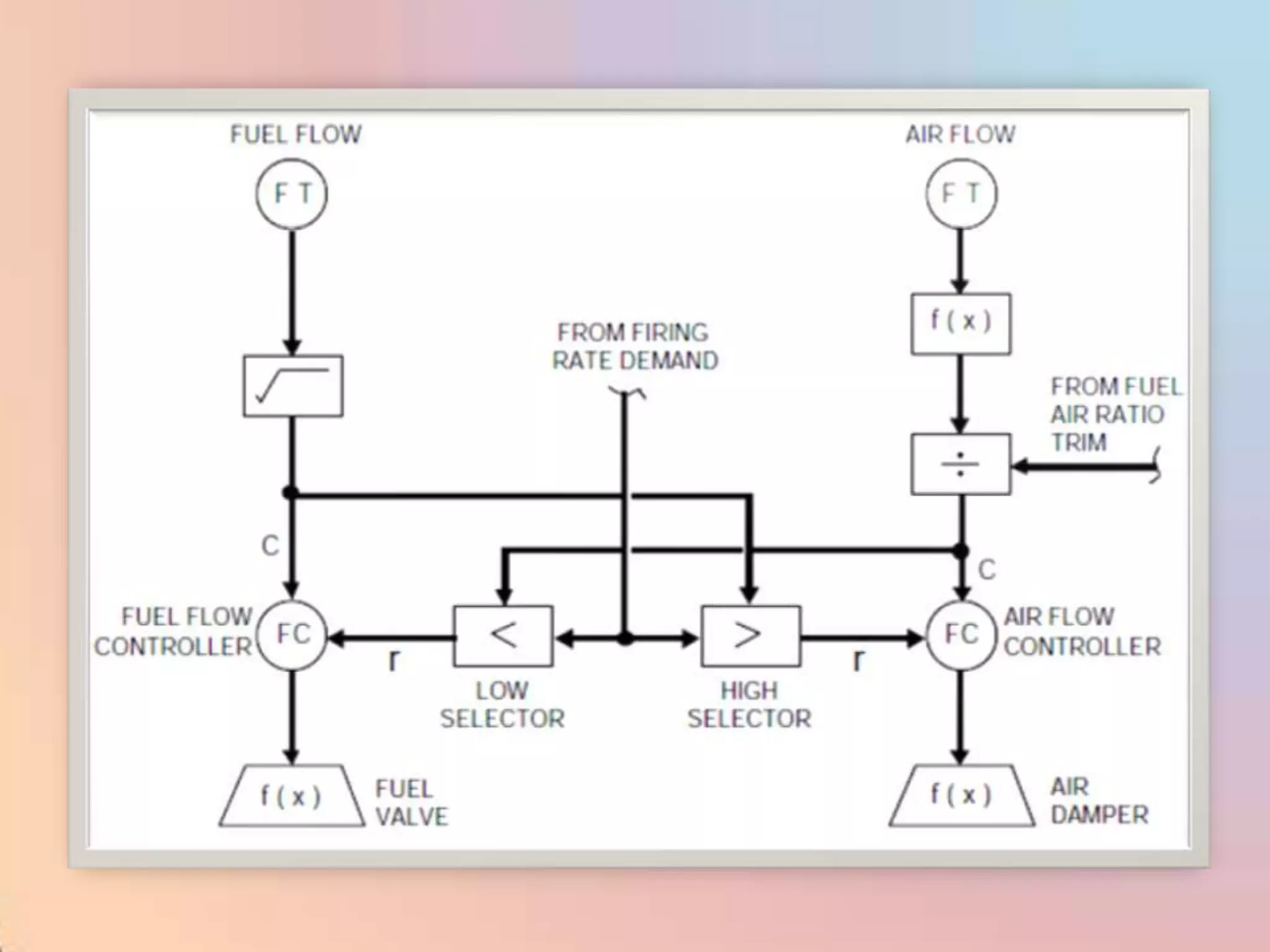









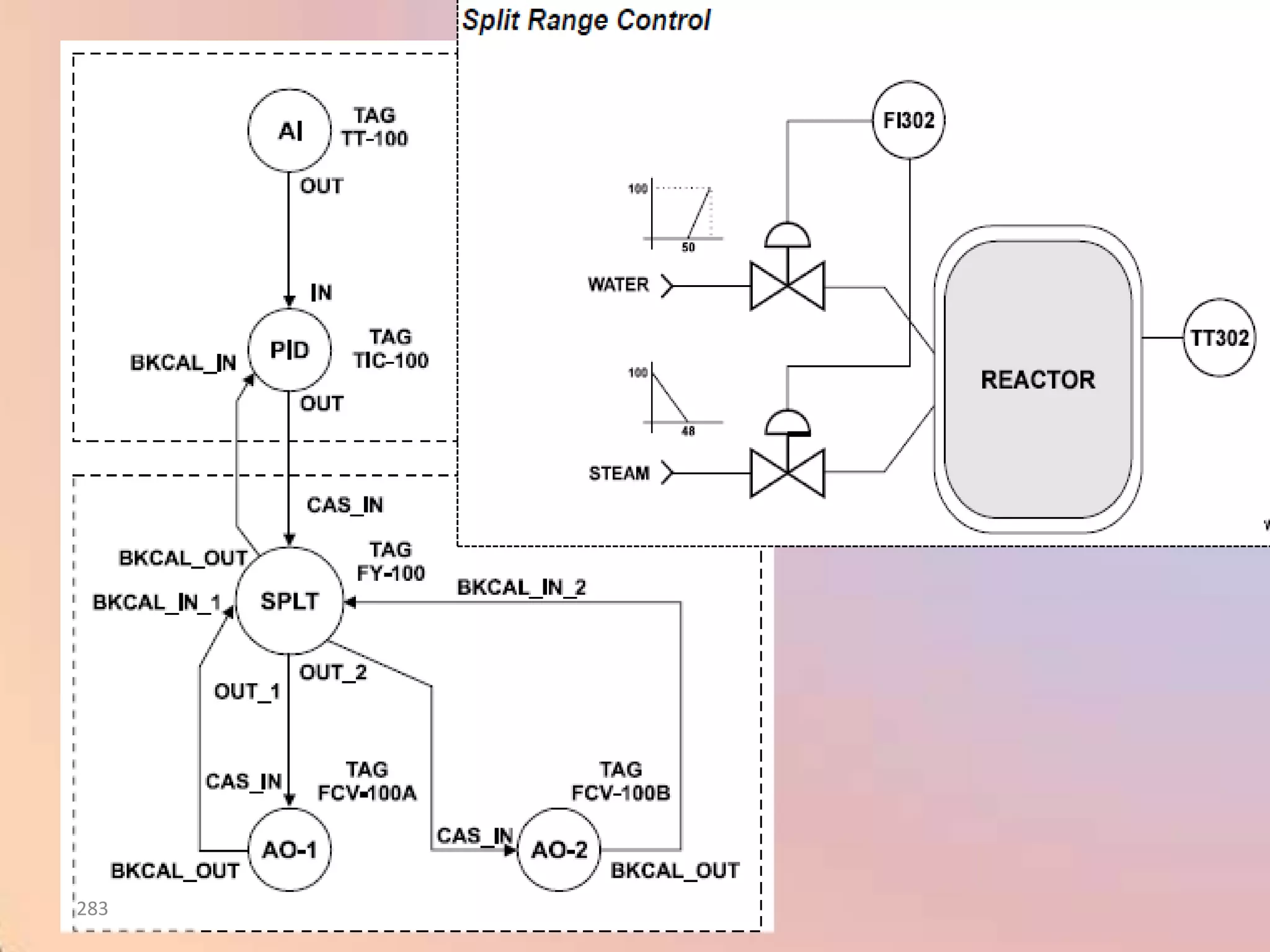
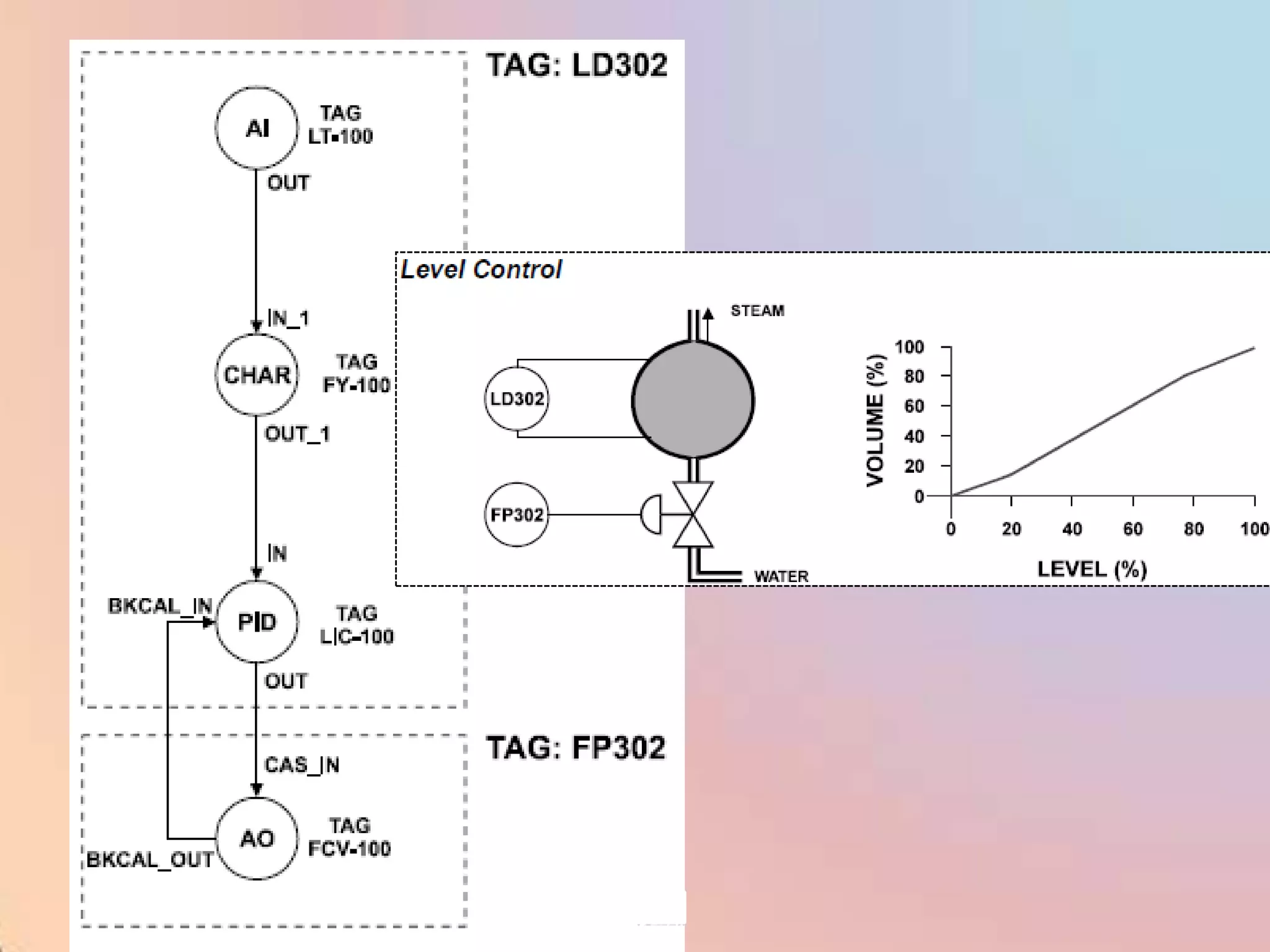
![CHAR - Signal Characterizer
•The block calculates OUT_1 from IN_1 and OUT_2 from IN_2, according to a curve
given by the points:
[x1 ;y1 ], [x2 ; y2 ]..............[x21 ; y21]
Where x corresponds to the Input and y to the Output.
•OUT_1 is related to IN_1 and OUT_2 is related to IN_2 using the same curve, but there
is no correlation between IN_1 and IN_2 or between OUT_1 and OUT_2.
273](https://image.slidesharecdn.com/industrialprocesscontrol-120310035732-phpapp02/75/Industrial-process-control-273-2048.jpg)