The document discusses periodic functions and their properties. The key points are: - A periodic function f(x) satisfies f(x) = f(x + T) for some fixed period T and all real x. - Periodic functions repeat their values at intervals of their period, including integer multiples of the period. - Functions are defined as even if f(-x) = f(x) and odd if f(-x) = -f(x). - Several important formulas are provided for integrating exponential and trigonometric functions.

1. Fourier Series
N. B. Vyas
Department of Mathematics,
Atmiya Institute of Tech. and Science,
Rajkot (Guj.) - INDIA
N. B. Vyas Fourier Series

2. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
N. B. Vyas Fourier Series

3. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
N. B. Vyas Fourier Series

4. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
N. B. Vyas Fourier Series

5. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
f (x) = f (x + T ) = f (x + 2T ) = . . . = f (x + nT )
N. B. Vyas Fourier Series

6. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
f (x) = f (x + T ) = f (x + 2T ) = . . . = f (x + nT )
f (x) = f (x − T ) = f (x − 2T ) = . . . = f (x − nT )
N. B. Vyas Fourier Series

7. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
f (x) = f (x + T ) = f (x + 2T ) = . . . = f (x + nT )
f (x) = f (x − T ) = f (x − 2T ) = . . . = f (x − nT )
∴ f (x) = f (x ± nT ), where n is a positive integer
N. B. Vyas Fourier Series

8. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
f (x) = f (x + T ) = f (x + 2T ) = . . . = f (x + nT )
f (x) = f (x − T ) = f (x − 2T ) = . . . = f (x − nT )
∴ f (x) = f (x ± nT ), where n is a positive integer
Eg. Sinx, Cosx, Secx and Cosecx are periodic functions with period
2π
N. B. Vyas Fourier Series

9. Periodic Function
A function f (x) which satisfies the relation f (x) = f (x + T ) for
all real x and some fixed T is called Periodic function.
The smallest positive number T , for which this relation holds, is
called the period of f (x).
If T is the period of f (x) then
f (x) = f (x + T ) = f (x + 2T ) = . . . = f (x + nT )
f (x) = f (x − T ) = f (x − 2T ) = . . . = f (x − nT )
∴ f (x) = f (x ± nT ), where n is a positive integer
Eg. Sinx, Cosx, Secx and Cosecx are periodic functions with period
2π
tanx and cotx are periodic functions with period π.
N. B. Vyas Fourier Series

10. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
N. B. Vyas Fourier Series

11. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
Eg. x2 and cosx are even function.
N. B. Vyas Fourier Series

12. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
Eg. x2 and cosx are even function.
c c
f (x)dx = 2 f (x)dx ; if f (x) is an even function.
−c 0
N. B. Vyas Fourier Series

13. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
Eg. x2 and cosx are even function.
c c
f (x)dx = 2 f (x)dx ; if f (x) is an even function.
−c 0
A function f (x) is said to be odd if f (−x) = −f (x).
N. B. Vyas Fourier Series

14. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
Eg. x2 and cosx are even function.
c c
f (x)dx = 2 f (x)dx ; if f (x) is an even function.
−c 0
A function f (x) is said to be odd if f (−x) = −f (x).
Eg. x3 and sinx are odd function.
N. B. Vyas Fourier Series

15. Even & Odd functions
A function f (x) is said to be even if f (−x) = f (x).
Eg. x2 and cosx are even function.
c c
f (x)dx = 2 f (x)dx ; if f (x) is an even function.
−c 0
A function f (x) is said to be odd if f (−x) = −f (x).
Eg. x3 and sinx are odd function.
c
f (x)dx = 0 ; if f (x) is an odd function.
−c
N. B. Vyas Fourier Series

16. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
N. B. Vyas Fourier Series

17. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
N. B. Vyas Fourier Series

18. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
c+2π
cos nx c+2π
sin nx dx = − = 0, n = 0
c n c
N. B. Vyas Fourier Series

19. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
c+2π
cos nx c+2π
sin nx dx = − = 0, n = 0
c n c
c+2π c+2π
sin nx
cos nx dx = = 0, n = 0
c n c
N. B. Vyas Fourier Series

20. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
c+2π
cos nx c+2π
sin nx dx = − = 0, n = 0
c n c
c+2π c+2π
sin nx
cos nx dx = = 0, n = 0
c n c
c+2π
1 c+2π
sin mx cos nx dx = 2sin mx cos nx dx
c 2 c
N. B. Vyas Fourier Series

21. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
c+2π
cos nx c+2π
sin nx dx = − = 0, n = 0
c n c
c+2π c+2π
sin nx
cos nx dx = = 0, n = 0
c n c
c+2π
1 c+2π
sin mx cos nx dx = 2sin mx cos nx dx
c 2 c
1 c+2π
= [sin (m + n)x + sin (m − n)x] dx
2 c
N. B. Vyas Fourier Series

22. Some Important Formula
eax
eax sin bx dx = (a sin bx − b cos bx) + c
a2 + b 2
eax
eax cos bx dx = 2 (a cosbx + b sinbx) + c
a + b2
c+2π
cos nx c+2π
sin nx dx = − = 0, n = 0
c n c
c+2π c+2π
sin nx
cos nx dx = = 0, n = 0
c n c
c+2π
1 c+2π
sin mx cos nx dx = 2sin mx cos nx dx
c 2 c
1 c+2π
= [sin (m + n)x + sin (m − n)x] dx
2 c
c+2π
1 cos (m + n)x cos (m − n)x
=− + = 0, n = 0
2 m+n m−n c
N. B. Vyas Fourier Series

23. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
N. B. Vyas Fourier Series

24. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
N. B. Vyas Fourier Series

25. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx
c
N. B. Vyas Fourier Series

26. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx
c
N. B. Vyas Fourier Series

27. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx = 0, n = 0
c
N. B. Vyas Fourier Series

28. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx = 0, n = 0
c
c+2π
cos2 nx dx
c
N. B. Vyas Fourier Series

29. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx = 0, n = 0
c
c+2π
cos2 nx dx = π
c
N. B. Vyas Fourier Series

30. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx = 0, n = 0
c
c+2π
cos2 nx dx = π
c
c+2π
sin2 nx dx
c
N. B. Vyas Fourier Series

31. Some Important Formula
c+2π c+2π
1
cos mx cos nx dx = 2
2cos mx cos nx dx
c c
c+2π
1
= 2
[cos (m + n)x + cos (m − n)x] dx
c
c+2π
1 sin (m + n)x sin (m − n)x
= 2
+ = 0, m = n
m+n m−n c
c+2π
sin mx sin nx dx = 0
c
c+2π
sin nx cos nx dx = 0, n = 0
c
c+2π
cos2 nx dx = π
c
c+2π
sin2 nx dx = π
c
N. B. Vyas Fourier Series

32. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
N. B. Vyas Fourier Series

33. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
N. B. Vyas Fourier Series

34. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
N. B. Vyas Fourier Series

35. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
N. B. Vyas Fourier Series

36. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
sin nπ = 0
N. B. Vyas Fourier Series

37. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
sin nπ = 0 and cos nπ = (−1)n
N. B. Vyas Fourier Series

38. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
sin nπ = 0 and cos nπ = (−1)n
sin n + 1 π = (−1)n
2
N. B. Vyas Fourier Series

39. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
sin nπ = 0 and cos nπ = (−1)n
sin n + 1 π = (−1)n and cos n +
2
1
2
π=0
N. B. Vyas Fourier Series

40. Some Important Formula
(Leibnitz’s Rule)To integrate the product of two
functions, one of which is power of x . We apply the
generalized rule of integration by parts
u vdx = u v1 − u v2 + u v3 − u v4 + . . .
Eg. x3 e−2x dx
e−2x e−2x e−2x e−2x
= x3 − 3x2 + 6x −6
−2 (−2)2 (−2)3 (−2)4
1
= − e−2x (4x3 + 6x2 + 6x + 3)
8
sin nπ = 0 and cos nπ = (−1)n
sin n + 1 π = (−1)n and cos n +
2
1
2
π=0
where n is integer.
N. B. Vyas Fourier Series

41. Fourier Series
The Fourier series for the function f (x) in the interval
c < x < c + 2π is given by
N. B. Vyas Fourier Series

42. Fourier Series
The Fourier series for the function f (x) in the interval
c < x < c + 2π is given by
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
N. B. Vyas Fourier Series

43. Fourier Series
The Fourier series for the function f (x) in the interval
c < x < c + 2π is given by
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
c+2π
1
where a0 = f (x) dx
π c
N. B. Vyas Fourier Series

44. Fourier Series
The Fourier series for the function f (x) in the interval
c < x < c + 2π is given by
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
c+2π
1
where a0 = f (x) dx
π c
c+2π
1
an = f (x) cos nx dx
π c
N. B. Vyas Fourier Series

45. Fourier Series
The Fourier series for the function f (x) in the interval
c < x < c + 2π is given by
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
c+2π
1
where a0 = f (x) dx
π c
c+2π
1
an = f (x) cos nx dx
π c
c+2π
1
bn = f (x) sin nx dx
π c
N. B. Vyas Fourier Series

46. Fourier Series
Corollary 1: If c = 0, the interval becomes 0 < x < 2π
N. B. Vyas Fourier Series

47. Fourier Series
Corollary 1: If c = 0, the interval becomes 0 < x < 2π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
N. B. Vyas Fourier Series

48. Fourier Series
Corollary 1: If c = 0, the interval becomes 0 < x < 2π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
2π
1
where a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

49. Fourier Series
Corollary 1: If c = 0, the interval becomes 0 < x < 2π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

50. Fourier Series
Corollary 1: If c = 0, the interval becomes 0 < x < 2π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

51. Fourier Series
Corollary 2: If c = −π, the interval becomes −π << π
N. B. Vyas Fourier Series

52. Fourier Series
Corollary 2: If c = −π, the interval becomes −π << π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
N. B. Vyas Fourier Series

53. Fourier Series
Corollary 2: If c = −π, the interval becomes −π << π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
π
1
where a0 = f (x) dx
π −π
N. B. Vyas Fourier Series

54. Fourier Series
Corollary 2: If c = −π, the interval becomes −π << π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
π
1
where a0 = f (x) dx
π −π
π
1
an = f (x) cos nx dx
π −π
N. B. Vyas Fourier Series

55. Fourier Series
Corollary 2: If c = −π, the interval becomes −π << π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
π
1
where a0 = f (x) dx
π −π
π
1
an = f (x) cos nx dx
π −π
π
1
bn = f (x) sin nx dx
π −π
N. B. Vyas Fourier Series

56. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
N. B. Vyas Fourier Series

57. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
N. B. Vyas Fourier Series

58. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
π
1
where a0 = f (x) dx = 0
π −π
N. B. Vyas Fourier Series

59. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π
where a0 = f (x) dx = 0
π −π
1 π
an = f (x) cos nx dx = 0
π −π
N. B. Vyas Fourier Series

60. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π
where a0 = f (x) dx = 0
π −π
1 π
an = f (x) cos nx dx = 0
π −π
because cos nx is an even function , f (x)cos nx is an odd
function
N. B. Vyas Fourier Series

61. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π
where a0 = f (x) dx = 0
π −π
1 π
an = f (x) cos nx dx = 0
π −π
because cos nx is an even function , f (x)cos nx is an odd
function
1 π 2 π
bn = f (x) sin nx dx = f (x) sin nx dx
π −π π 0
N. B. Vyas Fourier Series

62. Fourier Series
Special Case 1: If the interval is −c < x < c and f (x) is an
odd function i.e. f (−x) = −f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π
where a0 = f (x) dx = 0
π −π
1 π
an = f (x) cos nx dx = 0
π −π
because cos nx is an even function , f (x)cos nx is an odd
function
1 π 2 π
bn = f (x) sin nx dx = f (x) sin nx dx
π −π π 0
because sin nx is an odd function , f (x)sin nx is an even
function
N. B. Vyas Fourier Series

63. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
N. B. Vyas Fourier Series

64. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
N. B. Vyas Fourier Series

65. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
π π
1 2
where a0 = f (x) dx = f (x) dx
π −π π 0
N. B. Vyas Fourier Series

66. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π 2 π
where a0 = f (x) dx = f (x) dx
π −π π 0
1 π 2 π
an = f (x) cos nx dx = f (x) cos nx dx
π −π π 0
N. B. Vyas Fourier Series

67. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π 2 π
where a0 = f (x) dx = f (x) dx
π −π π 0
1 π 2 π
an = f (x) cos nx dx = f (x) cos nx dx
π −π π 0
because cos nx is an even function , f (x)cos nx is an even
function
N. B. Vyas Fourier Series

68. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π 2 π
where a0 = f (x) dx = f (x) dx
π −π π 0
1 π 2 π
an = f (x) cos nx dx = f (x) cos nx dx
π −π π 0
because cos nx is an even function , f (x)cos nx is an even
function
1 π
bn = f (x) sin nx dx = 0
π −π
N. B. Vyas Fourier Series

69. Fourier Series
Special Case 2: If the interval is −c < x < c and f (x) is an
even function i.e. f (−x) = f (x). Let C = π
∞ ∞
a0
f (x) = + an cos nx + bn sin nx
2 n=1 n=1
1 π 2 π
where a0 = f (x) dx = f (x) dx
π −π π 0
1 π 2 π
an = f (x) cos nx dx = f (x) cos nx dx
π −π π 0
because cos nx is an even function , f (x)cos nx is an even
function
1 π
bn = f (x) sin nx dx = 0
π −π
because sin nx is an odd function , f (x)sin nx is an odd
function
N. B. Vyas Fourier Series

70. Example
2
π−x
Ex. Obtain Fourier series of f (x) = in the
2
interval 0 ≤ x ≤ 2π. Hence deduce that
π2 1 1 1
= 2 − 2 + 2 − ...
12 1 2 3
N. B. Vyas Fourier Series

71. Example
2
π−x
Ex. Obtain Fourier series of f (x) = in the
2
interval 0 ≤ x ≤ 2π. Hence deduce that
π2 1 1 1
= 2 − 2 + 2 − ...
12 1 2 3
N. B. Vyas Fourier Series

72. Example
Sol. Step 1. The Fourier series of f (x) is given by
N. B. Vyas Fourier Series

73. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
N. B. Vyas Fourier Series

74. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

75. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

76. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

77. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

78. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

79. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
2π
1 (π − x)2
a0 = dx
π 0 4
N. B. Vyas Fourier Series

80. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
2π
1 (π − x)2
a0 = dx
π 0 4
2π
1 (π − x)3 1
= =− (−π 3 − π 3 )
4π (−3) 0 12π
N. B. Vyas Fourier Series

81. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
2π
1 (π − x)2
a0 = dx
π 0 4
2π
1 (π − x)3 1
= =− (−π 3 − π 3 )
4π (−3) 0 12π
2
π
=
6
N. B. Vyas Fourier Series

82. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

83. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
2π
1 (π − x)2
an = cos nx dx
π 0 4
N. B. Vyas Fourier Series

84. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
2π
1 (π − x)2
an = cos nx dx
π 0 4
1
= 2
n
N. B. Vyas Fourier Series

85. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

86. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
2π
1 (π − x)2
bn = sin nx dx
π 0 4
N. B. Vyas Fourier Series

87. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
2π
1 (π − x)2
bn = sin nx dx
π 0 4
=0
N. B. Vyas Fourier Series

88. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
N. B. Vyas Fourier Series

89. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
2 ∞
π−x π2 1
= + cos nx
2 12 n=1 n2
N. B. Vyas Fourier Series

90. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
2 ∞
π−x π2 1
= + cos nx
2 12 n=1 n2
π2 1 1 1
= + 2 cos x + 2 cos 2x + 2 cos 3x + . . .
12 1 2 3
N. B. Vyas Fourier Series

91. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
2 ∞
π−x π2 1
= + cos nx
2 12 n=1 n2
π2 1 1 1
= + 2 cos x + 2 cos 2x + 2 cos 3x + . . .
12 1 2 3
Putting x = π, we get
N. B. Vyas Fourier Series

92. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
2 ∞
π−x π2 1
= + cos nx
2 12 n=1 n2
π2 1 1 1
= + 2 cos x + 2 cos 2x + 2 cos 3x + . . .
12 1 2 3
Putting x = π, we get
π2 1 1 1 1
0= − 2 + 2 − 2 + 2 − ...
12 1 2 3 4
N. B. Vyas Fourier Series

93. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
2 ∞
π−x π2 1
= + cos nx
2 12 n=1 n2
π2 1 1 1
= + 2 cos x + 2 cos 2x + 2 cos 3x + . . .
12 1 2 3
Putting x = π, we get
π2 1 1 1 1
0= − 2 + 2 − 2 + 2 − ...
12 1 2 3 4
π2 1 1 1 1
= 2 − 2 + 2 − 2 + ...
12 1 2 3 4
N. B. Vyas Fourier Series

94. Example
Ex. Expand in a Fourier series the function f (x) = x
in the interval 0 ≤ x ≤ 2π.
N. B. Vyas Fourier Series

95. Example
Ex. Expand in a Fourier series the function f (x) = x
in the interval 0 ≤ x ≤ 2π.
N. B. Vyas Fourier Series

96. Example
Sol. Step 1. The Fourier series of f (x) is given by
N. B. Vyas Fourier Series

97. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
N. B. Vyas Fourier Series

98. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

99. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

100. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

101. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

102. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

103. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
2π
1
a0 = x dx
π 0
N. B. Vyas Fourier Series

104. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
2π
1
a0 = x dx
π 0
2 2π
1 x
=
4π 2 0
N. B. Vyas Fourier Series

105. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
2π
1
a0 = x dx
π 0
2 2π
1 x
=
4π 2 0
= 2π
N. B. Vyas Fourier Series

106. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

107. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
2π
1
an = x cos nx dx
π 0
N. B. Vyas Fourier Series

108. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x cos nx dx
π 0
2π
sin nx cos nx
x − −
n n 0
N. B. Vyas Fourier Series

109. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x cos nx dx
π 0
2π
sin nx cos nx
x − −
n n 0
=0
N. B. Vyas Fourier Series

110. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

111. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
2π
1
bn = x sin nx dx
π 0
N. B. Vyas Fourier Series

112. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
2π
1
bn = x sin nx dx
π 0
−2
=
n
N. B. Vyas Fourier Series

113. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
N. B. Vyas Fourier Series

114. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
∞
2π −2
f (x) = +0+ sin nx
2 n=1
n
N. B. Vyas Fourier Series

115. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
∞
2π −2
f (x) = +0+ sin nx
2 n=1
n
∞
sin nx
=π−
n=1
n
N. B. Vyas Fourier Series

116. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval [0, 2π]
∞
2π −2
f (x) = +0+ sin nx
2 n=1
n
∞
sin nx
=π−
n=1
n
N. B. Vyas Fourier Series

117. Example
Ex. Determine the Fourier series expansion of the
function f (x) = xsin x in the interval 0 ≤ x ≤ 2π.
N. B. Vyas Fourier Series

118. Example
Ex. Determine the Fourier series expansion of the
function f (x) = xsin x in the interval 0 ≤ x ≤ 2π.
N. B. Vyas Fourier Series

119. Example
Sol. Step 1. The Fourier series of f (x) is given by
N. B. Vyas Fourier Series

120. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
N. B. Vyas Fourier Series

121. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

122. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

123. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

124. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
2π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

125. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

126. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
2π
1
a0 = x sin x dx
π 0
N. B. Vyas Fourier Series

127. Example
2π
1
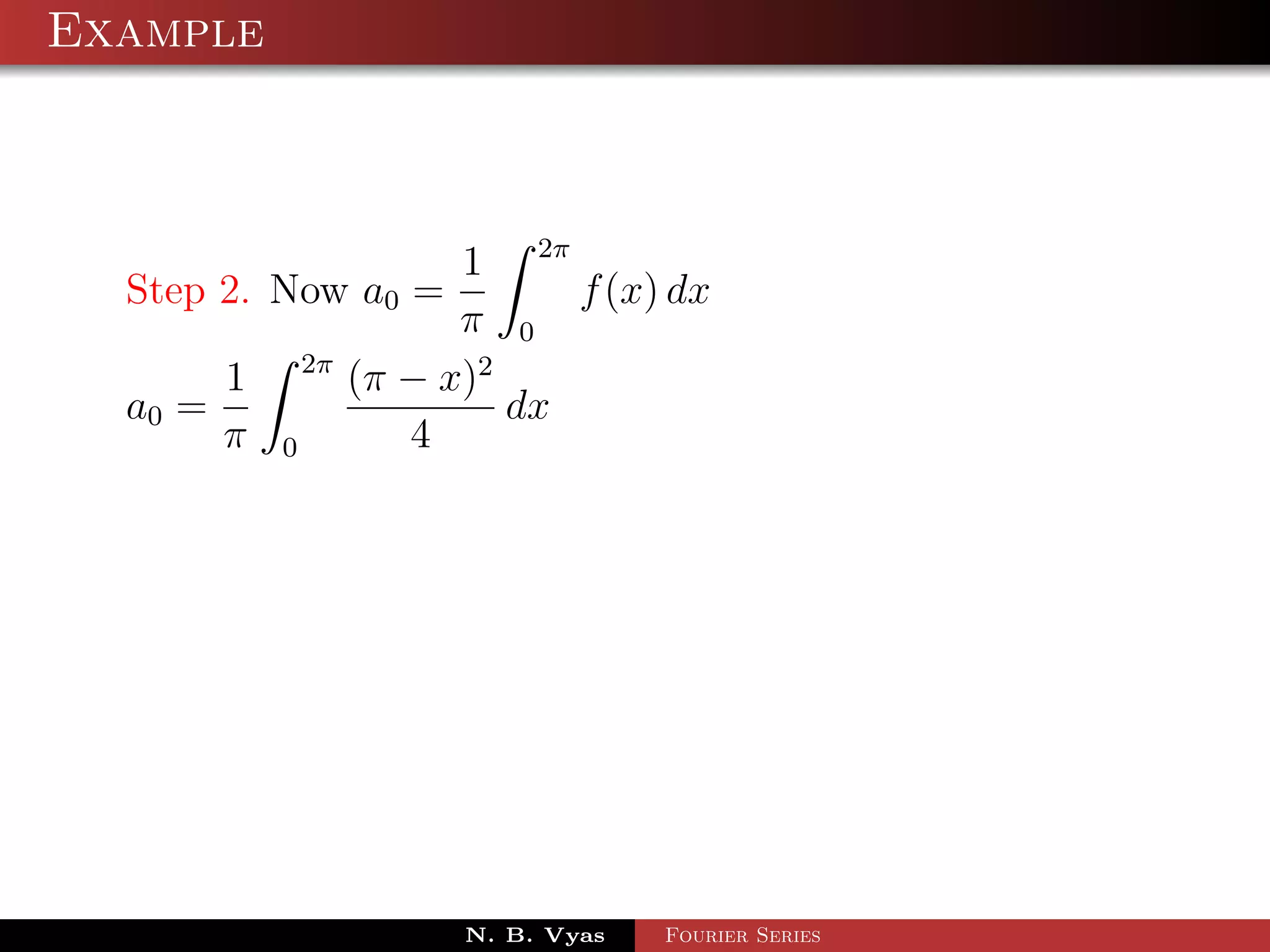
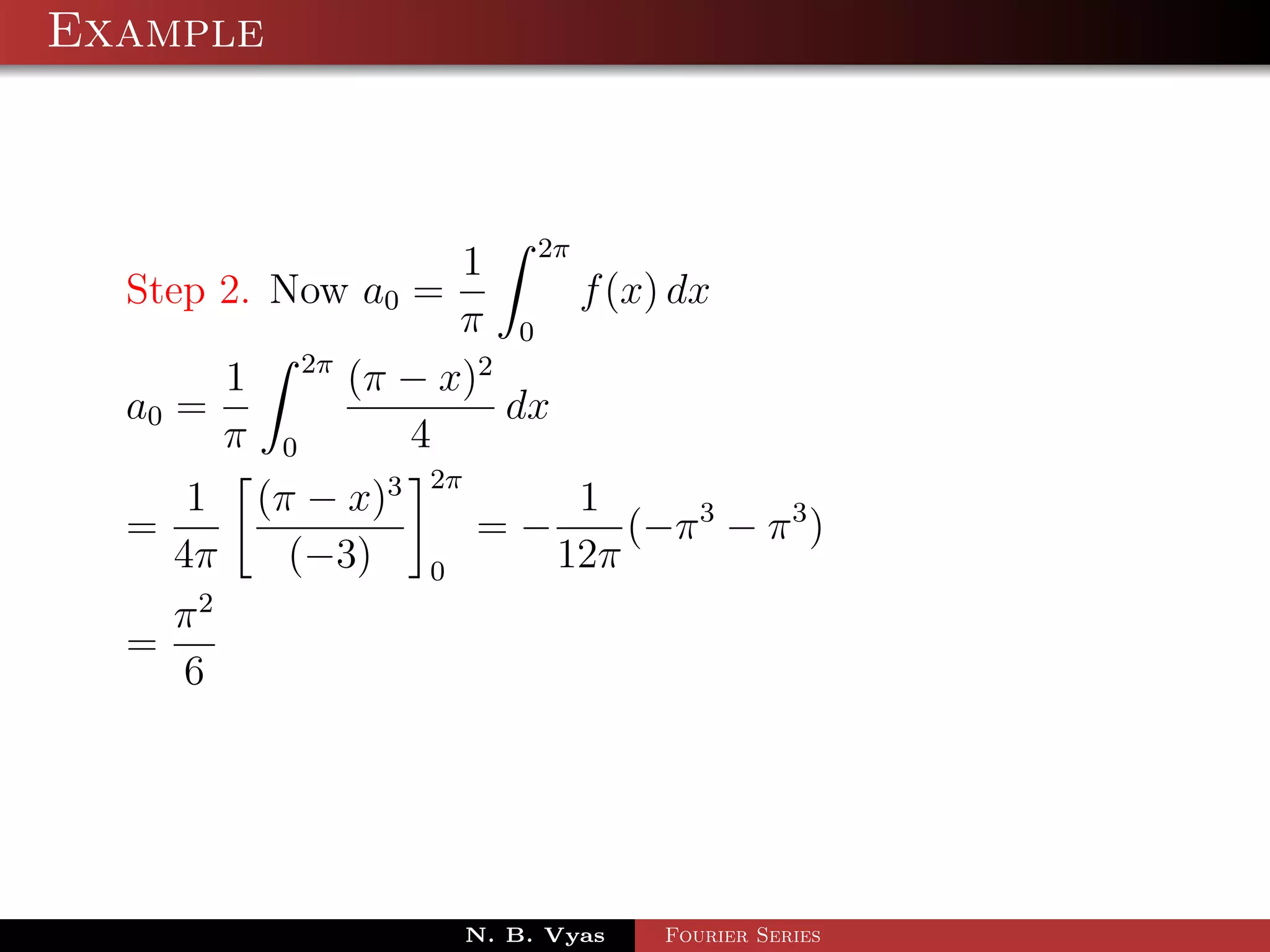
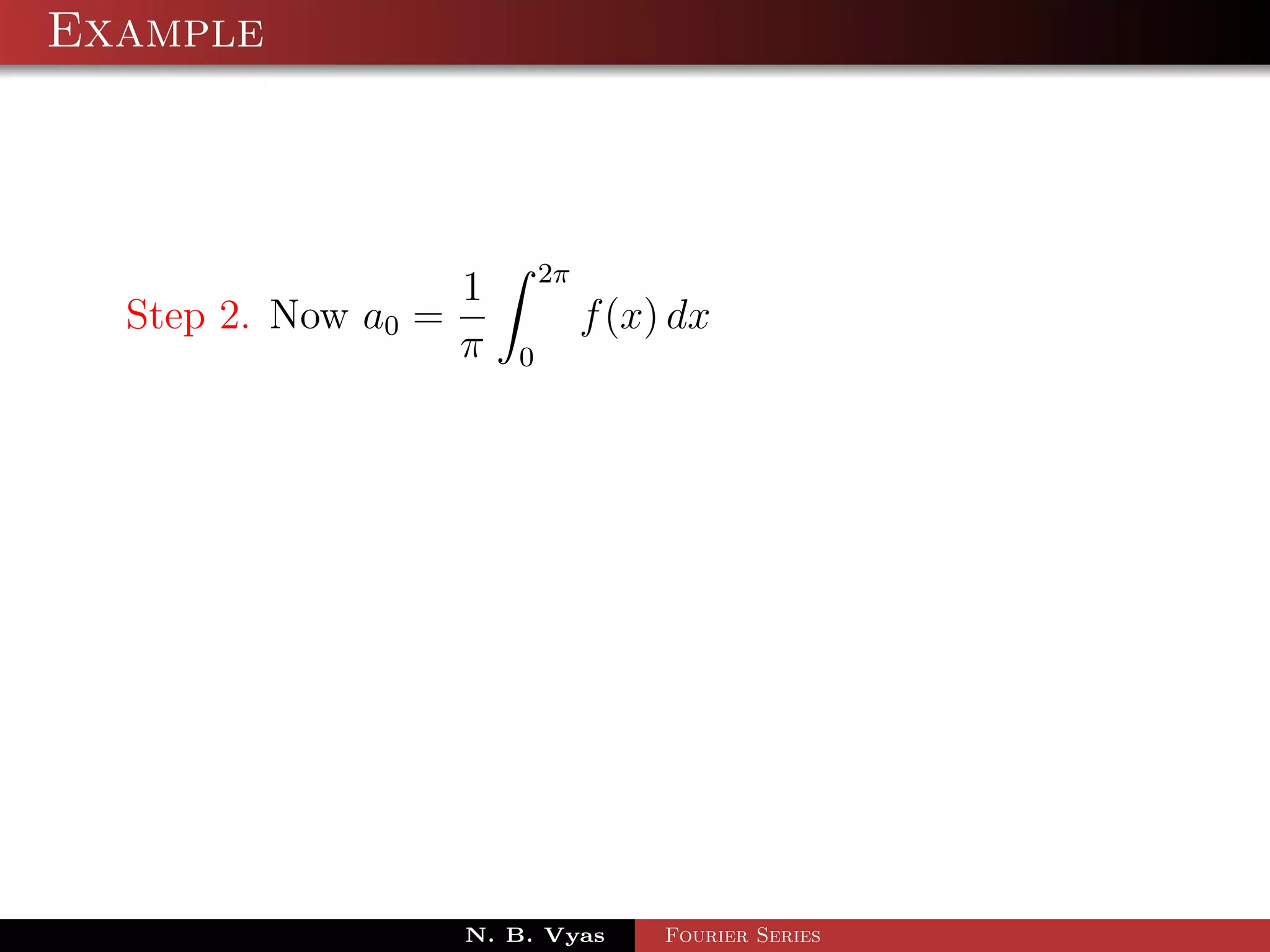
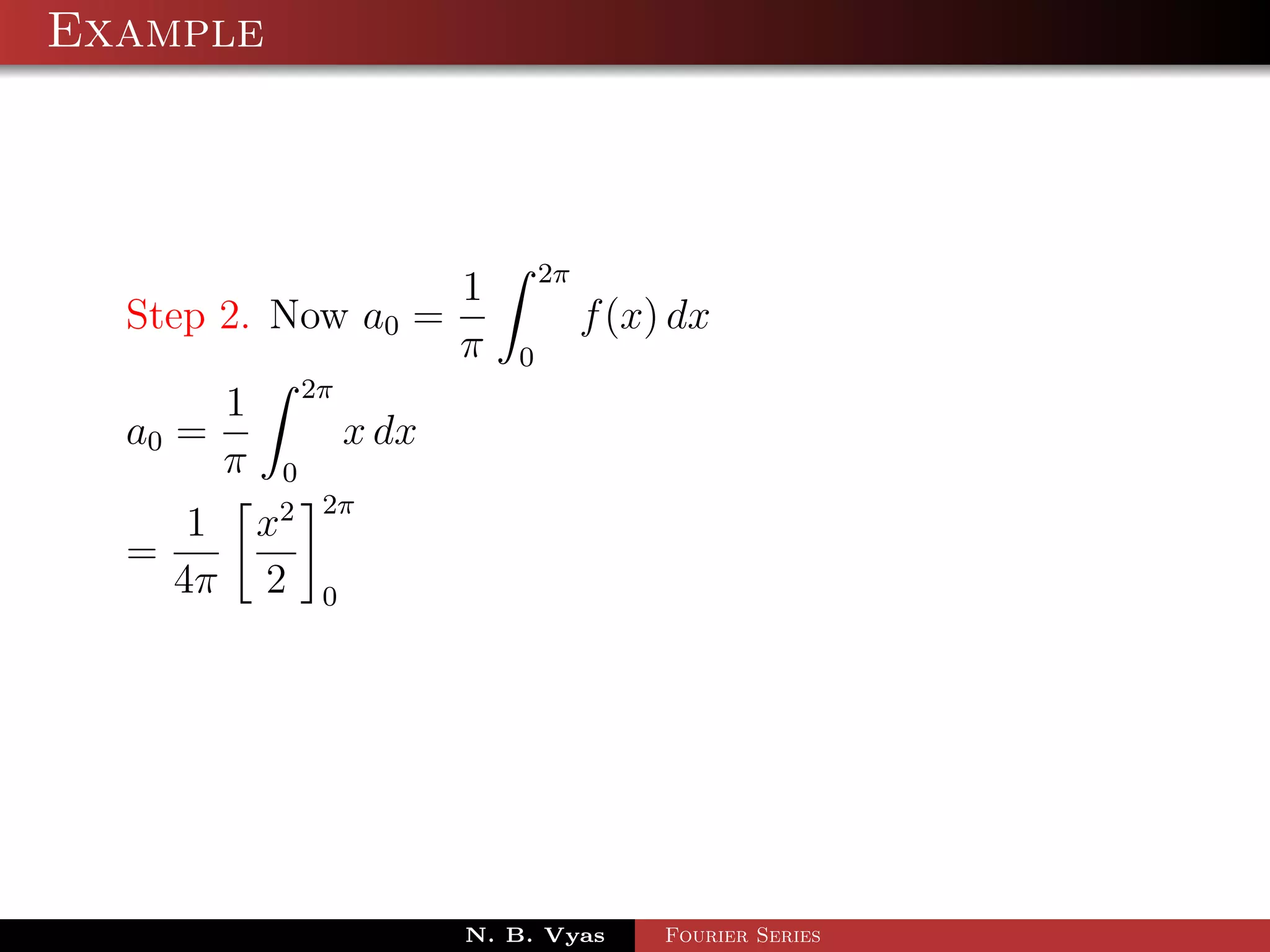
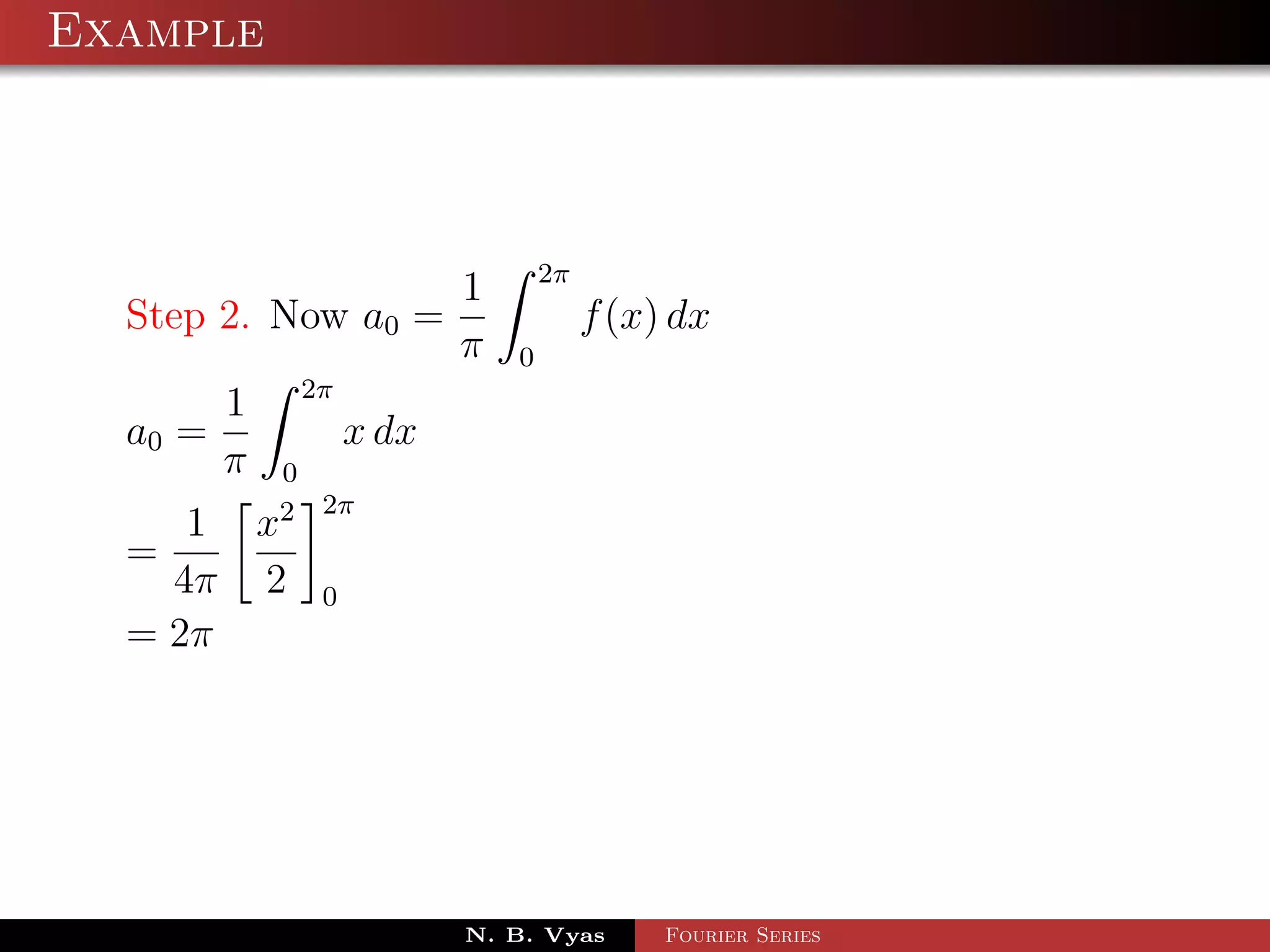
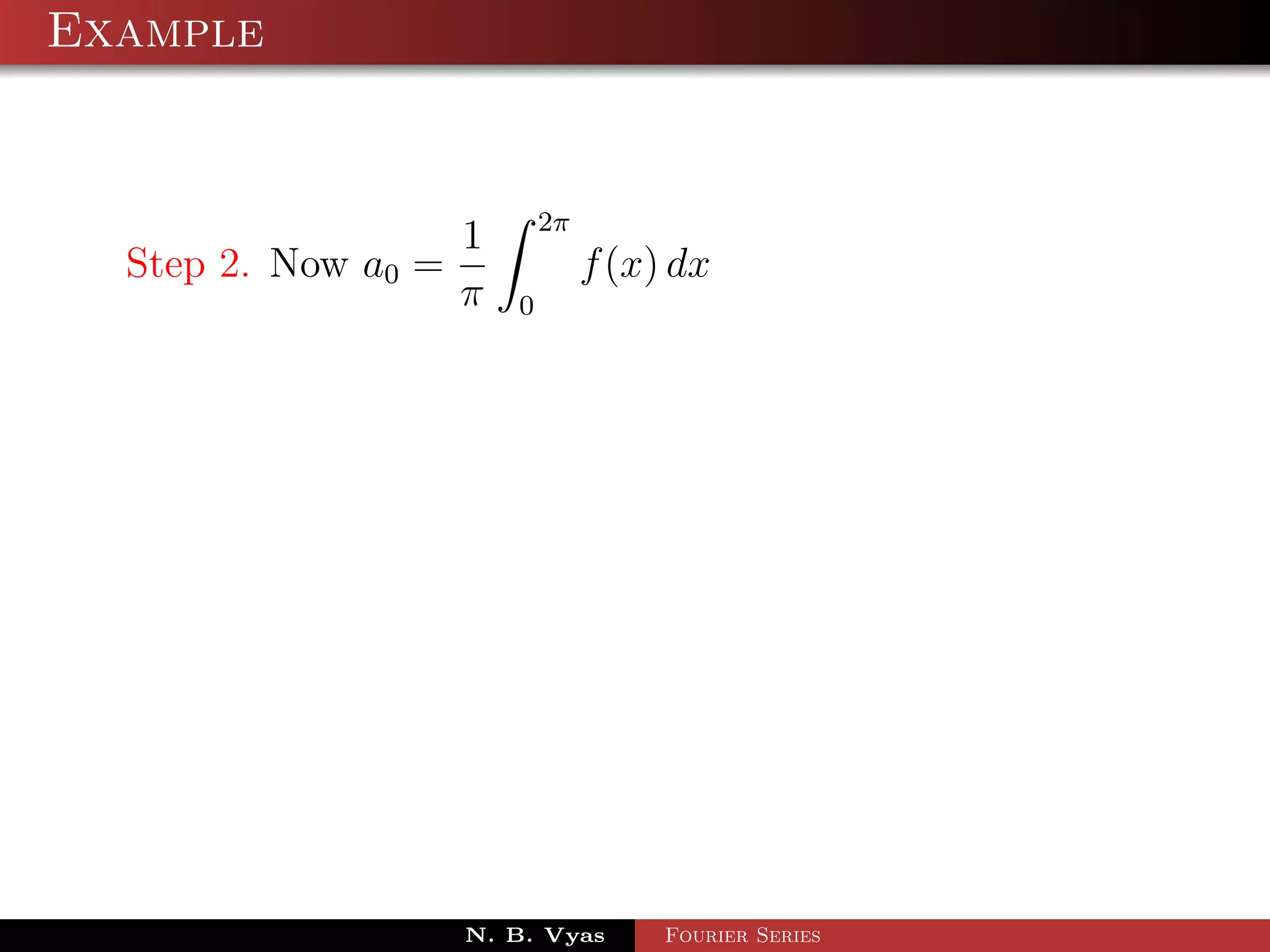
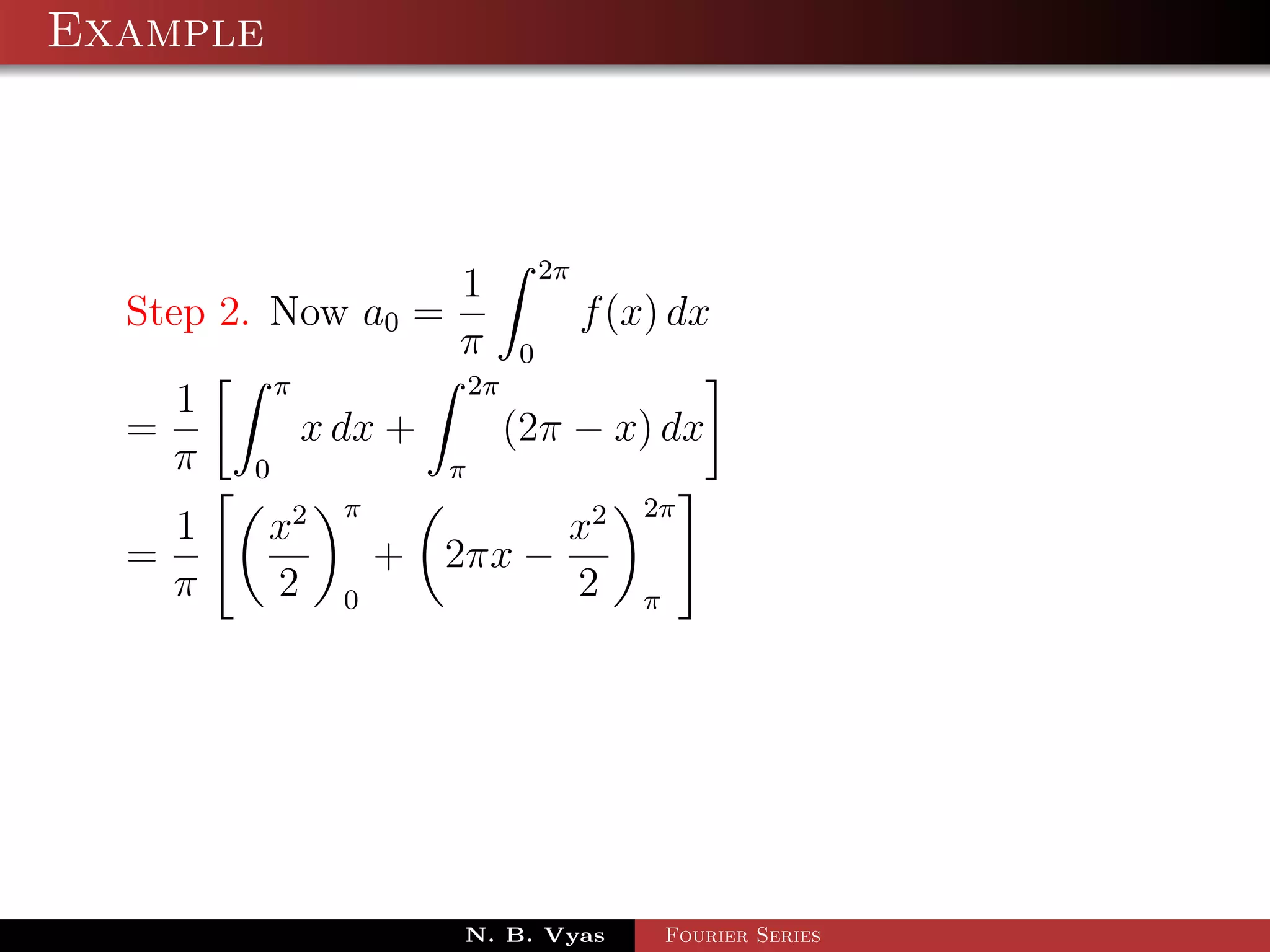
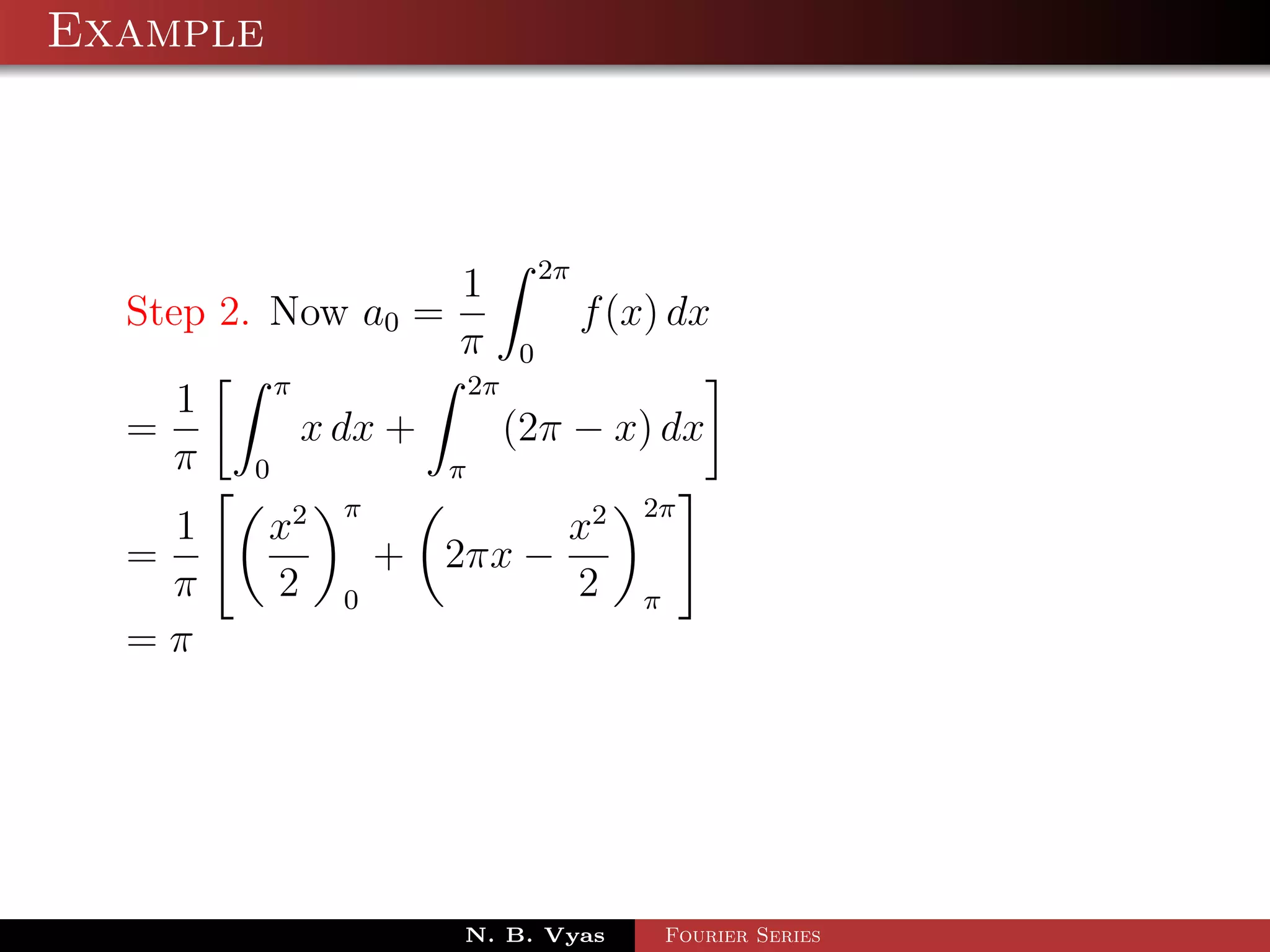
Step 2. Now a0 = f (x) dx
π 0
1 2π
a0 = x sin x dx
π 0
1
= [−x cos x + sin x]2π
0
π
N. B. Vyas Fourier Series

128. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
1 2π
a0 = x sin x dx
π 0
1
= [−x cos x + sin x]2π
0
π
1
= (−2 π cos 2π + sin 2π − 0 + sin 0)
π
N. B. Vyas Fourier Series

129. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
1 2π
a0 = x sin x dx
π 0
1
= [−x cos x + sin x]2π
0
π
1
= (−2 π cos 2π + sin 2π − 0 + sin 0)
π
−2π
a0 = = −2
π
N. B. Vyas Fourier Series

130. Example
2π
1
Step 3. an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

131. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x sin x cos nx dx
π 0
N. B. Vyas Fourier Series

132. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x sin x cos nx dx
π 0
2π
1
= x (2 sin x cos nx) dx
2π 0
N. B. Vyas Fourier Series

133. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x sin x cos nx dx
π 0
2π
1
= x (2 sin x cos nx) dx
2π 0
2π
1
= x (sin (n + 1)x − sin (n − 1)x) dx
2π 0
N. B. Vyas Fourier Series

134. Example
1 2π
Step 3. an = f (x) cos nx dx
π 0
1 2π
an = x sin x cos nx dx
π 0
2π
1
= x (2 sin x cos nx) dx
2π 0
2π
1
= x (sin (n + 1)x − sin (n − 1)x) dx
2π 0
2π 2π
1 1
= x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
N. B. Vyas Fourier Series

135. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
N. B. Vyas Fourier Series

136. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
N. B. Vyas Fourier Series

137. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1
∴ a1 = x sin 2x dx
2π 0
N. B. Vyas Fourier Series

138. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1
∴ a1 = x sin 2x dx
2π 0
2π
1 cos 2x sin 2x
= −x +
2π 2 4 0
N. B. Vyas Fourier Series

139. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1
∴ a1 = x sin 2x dx
2π 0
2π
1 cos 2x sin 2x
= −x +
2π 2 4 0
1
=−
2
N. B. Vyas Fourier Series

140. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
N. B. Vyas Fourier Series

141. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
N. B. Vyas Fourier Series

142. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1 cos (n + 1)x sin (n + 1)x
∴ an = x − − −
2π n+1 (n + 1)2 0
N. B. Vyas Fourier Series

143. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1 cos (n + 1)x sin (n + 1)x
∴ an = x − − −
2π n+1 (n + 1)2 0
2π
1 cos (n − 1)x sin (n − 1)x
− x − − −
2π n−1 (n − 1)2 0
N. B. Vyas Fourier Series

144. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1 cos (n + 1)x sin (n + 1)x
∴ an = x − − −
2π n+1 (n + 1)2 0
2π
1 cos (n − 1)x sin (n − 1)x
− x − − −
2π n−1 (n − 1)2 0
1 2π 2π
= − +0+ −0
2π n+1 n−1
N. B. Vyas Fourier Series

145. Example
2π 2π
1 1
an = x sin (n + 1)x dx − x sin (n − 1)x dx
2π 0 2π 0
If n = 1
2π
1 cos (n + 1)x sin (n + 1)x
∴ an = x − − −
2π n+1 (n + 1)2 0
2π
1 cos (n − 1)x sin (n − 1)x
− x − − −
2π n−1 (n − 1)2 0
1 2π 2π
= − +0+ −0
2π n+1 n−1
2
= 2
n −1
N. B. Vyas Fourier Series

146. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

147. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
2π
1
= x sin x sin nx dx
π 0
N. B. Vyas Fourier Series

148. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
2π
1
= x sin x sin nx dx
π 0
2π
1
= x (2sin nx sin x) dx
2π 0
N. B. Vyas Fourier Series

149. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
2π
1
= x sin x sin nx dx
π 0
2π
1
= x (2sin nx sin x) dx
2π 0
2π
1
= x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
N. B. Vyas Fourier Series

150. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
N. B. Vyas Fourier Series

151. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
N. B. Vyas Fourier Series

152. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π 2π
1 1
∴ b1 = (−x cos 2x) dx + x dx
2π 0 2π 0
N. B. Vyas Fourier Series

153. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π 2π
1 1
∴ b1 = (−x cos 2x) dx + x dx
2π 0 2π 0
2π
1 sin 2x cos 2x x2
= x − − +
2π 2 4 2 0
N. B. Vyas Fourier Series

154. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π 2π
1 1
∴ b1 = (−x cos 2x) dx + x dx
2π 0 2π 0
2π
1 sin 2x cos 2x x2
= x − − +
2π 2 4 2 0
b1 = π
N. B. Vyas Fourier Series

155. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
N. B. Vyas Fourier Series

156. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
N. B. Vyas Fourier Series

157. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π
1 sin (n + 1)x cos (n + 1)x
∴ bn = x − −
2π n+1 (n + 1)2 0
N. B. Vyas Fourier Series

158. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π
1 sin (n + 1)x cos (n + 1)x
∴ bn = x − −
2π n+1 (n + 1)2 0
2π
1 sin (n − 1)x cos (n − 1)x
+ x +
2π n−1 (n − 1)2 0
N. B. Vyas Fourier Series

159. Example
2π
1
bn = x (−cos (n + 1)x + cos (n − 1)x) dx
2π 0
If n = 1
2π
1 sin (n + 1)x cos (n + 1)x
∴ bn = x − −
2π n+1 (n + 1)2 0
2π
1 sin (n − 1)x cos (n − 1)x
+ x +
2π n−1 (n − 1)2 0
=0
N. B. Vyas Fourier Series

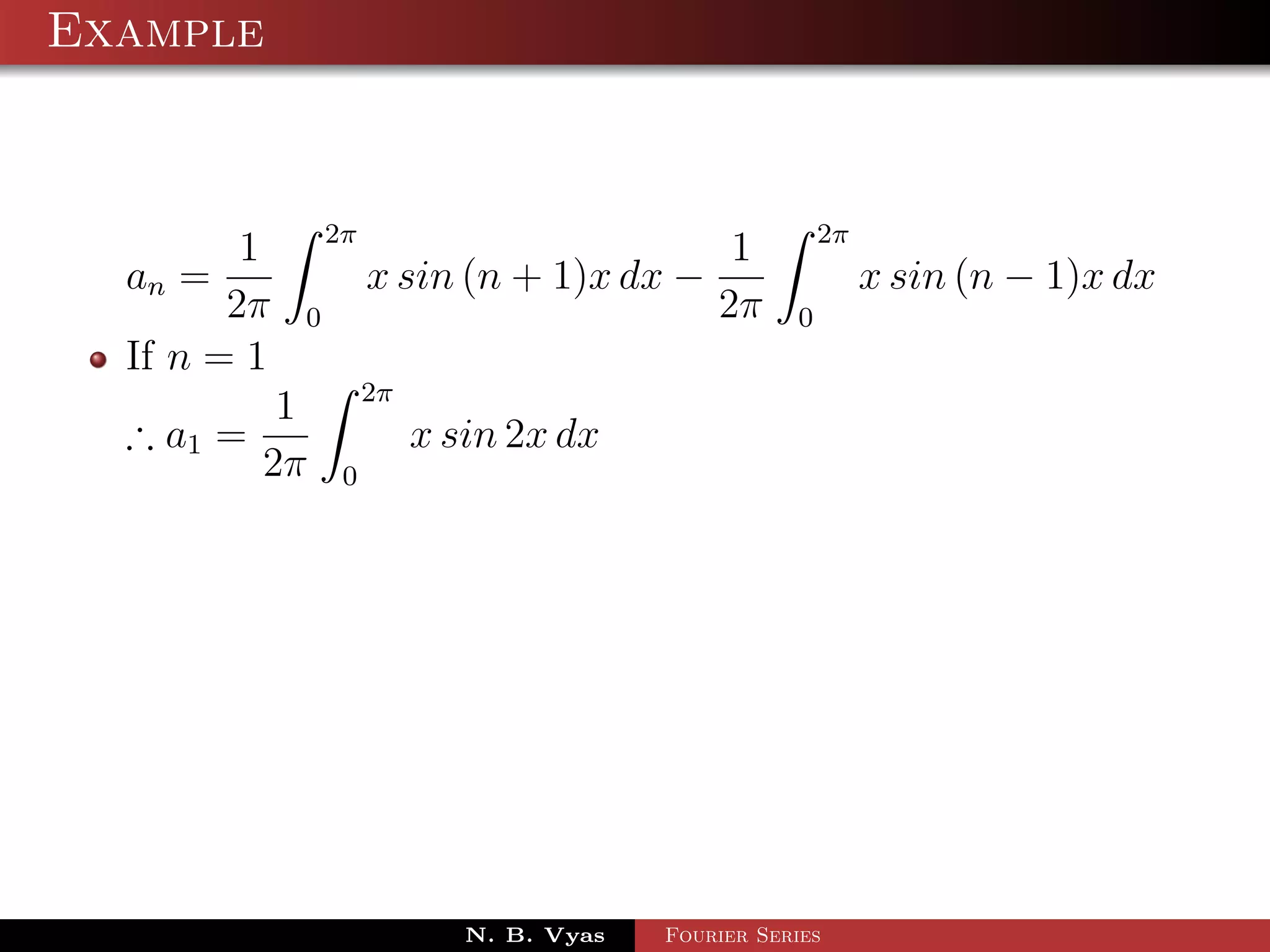
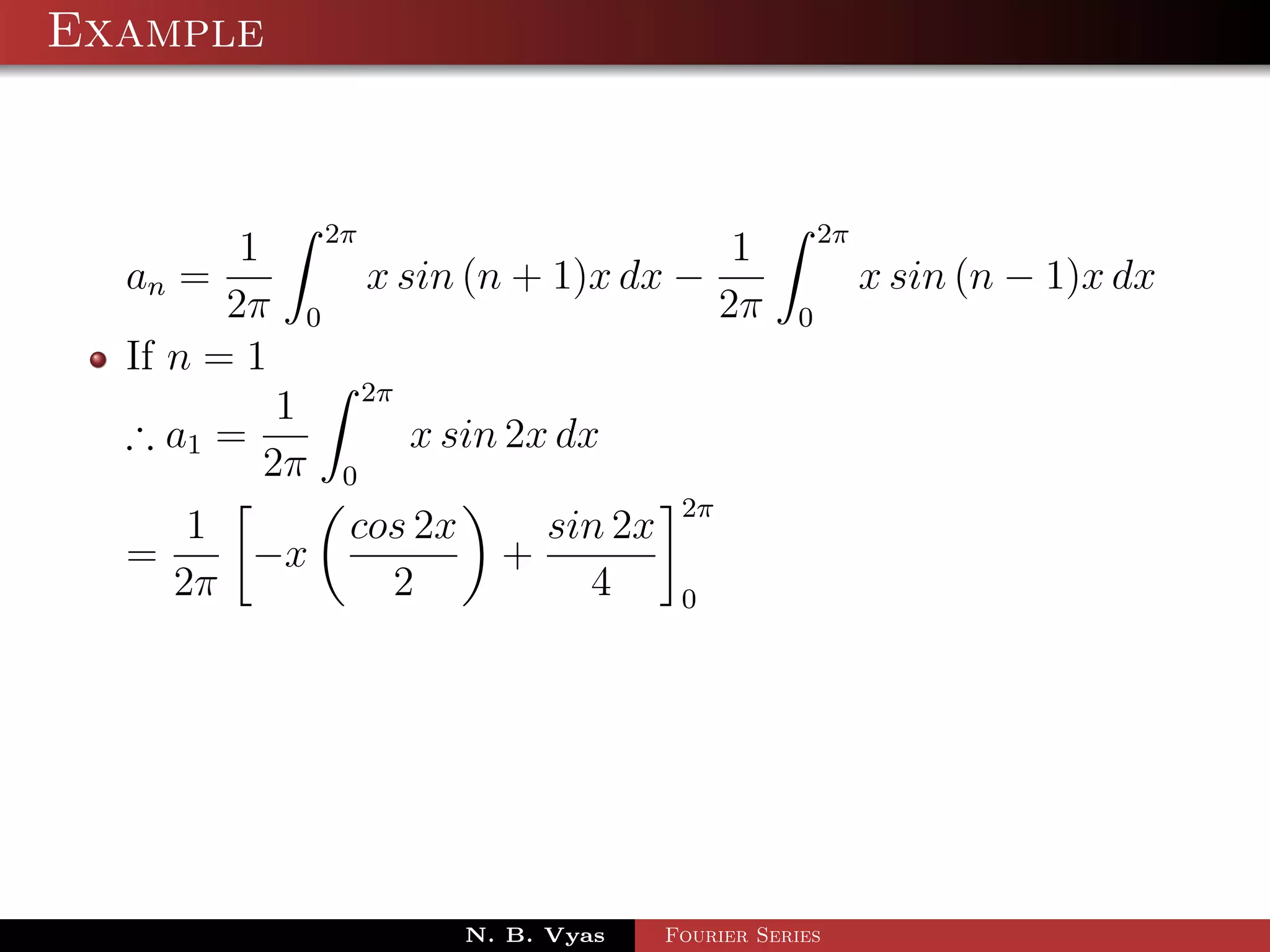
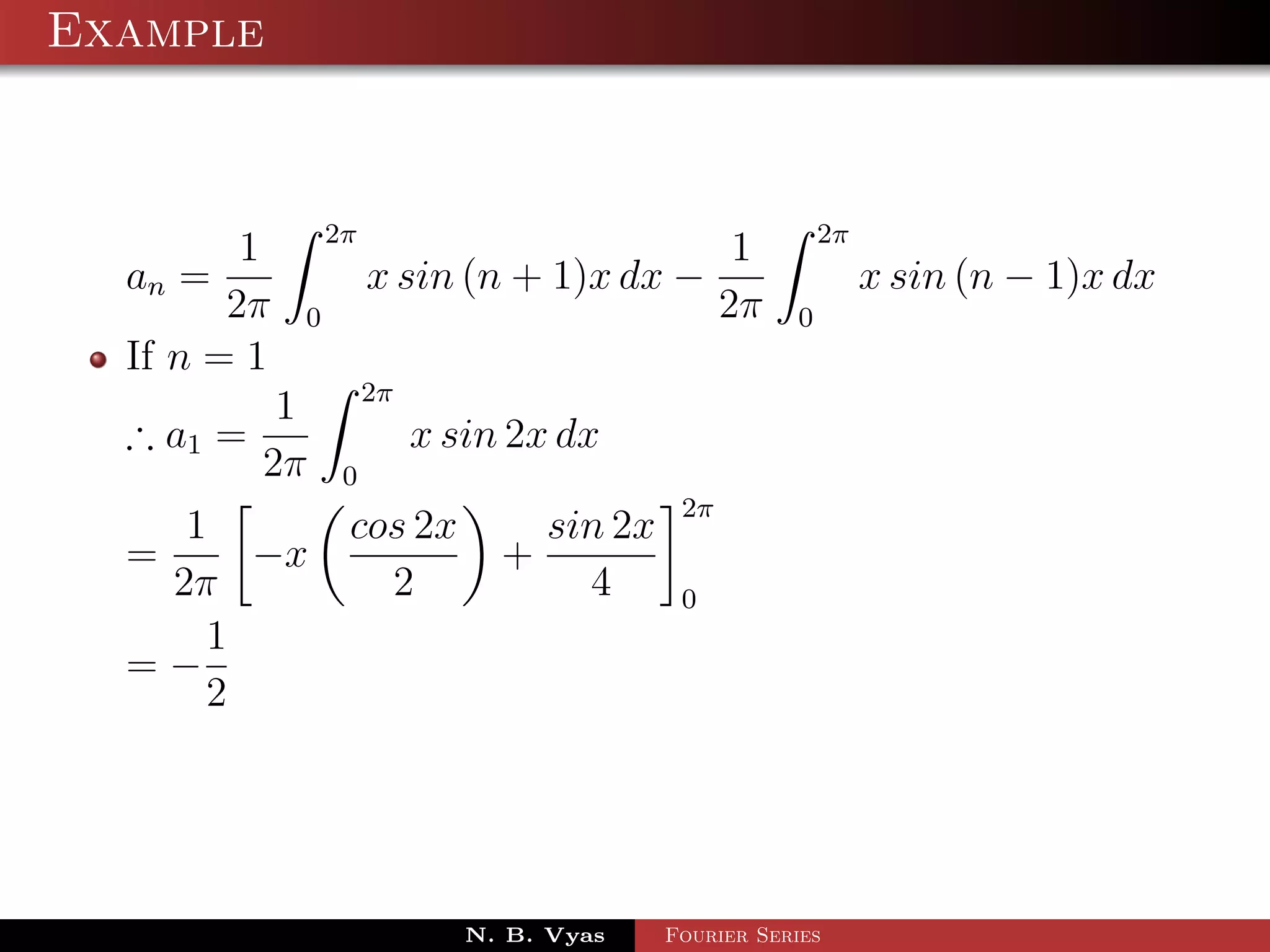
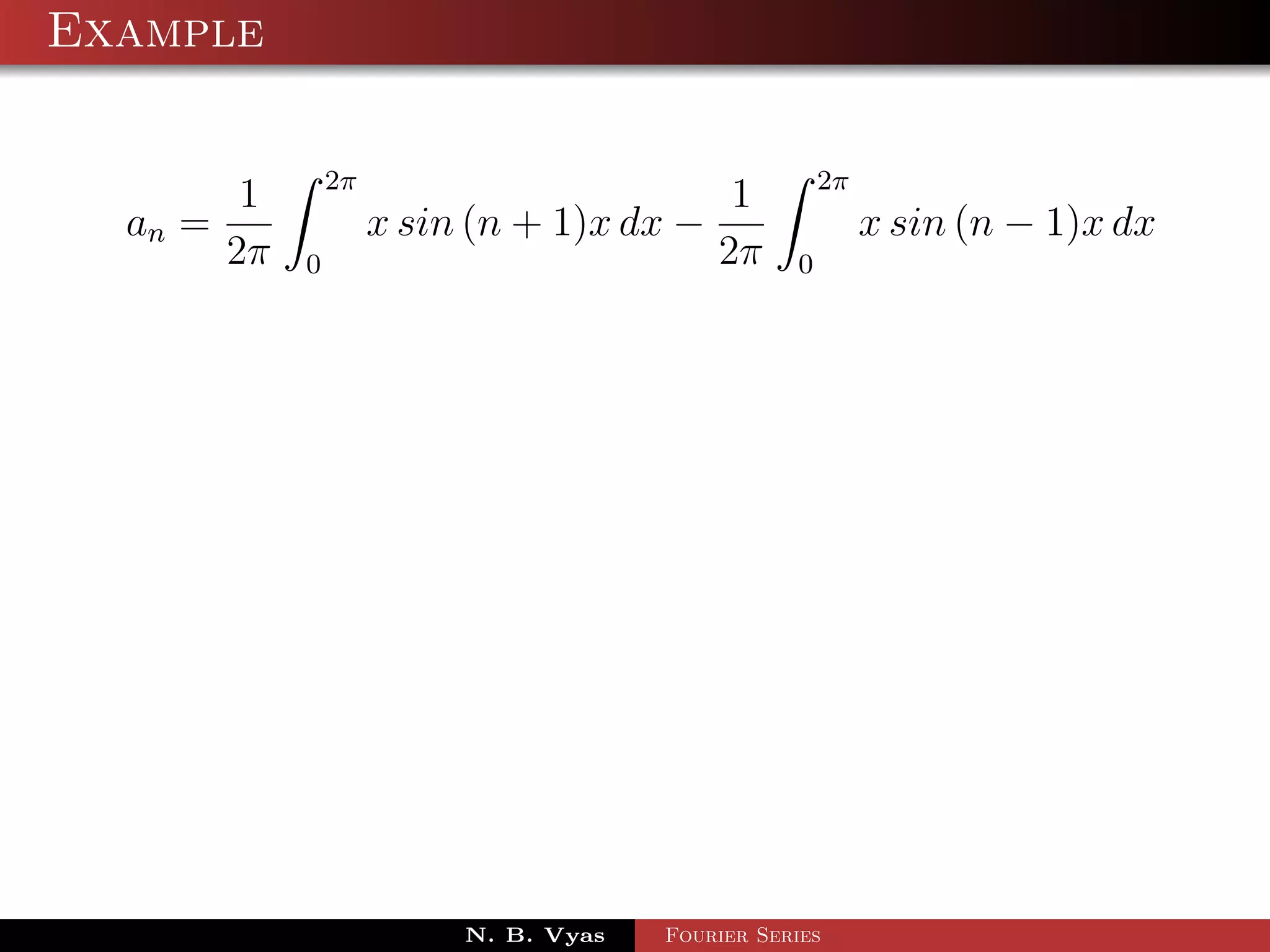
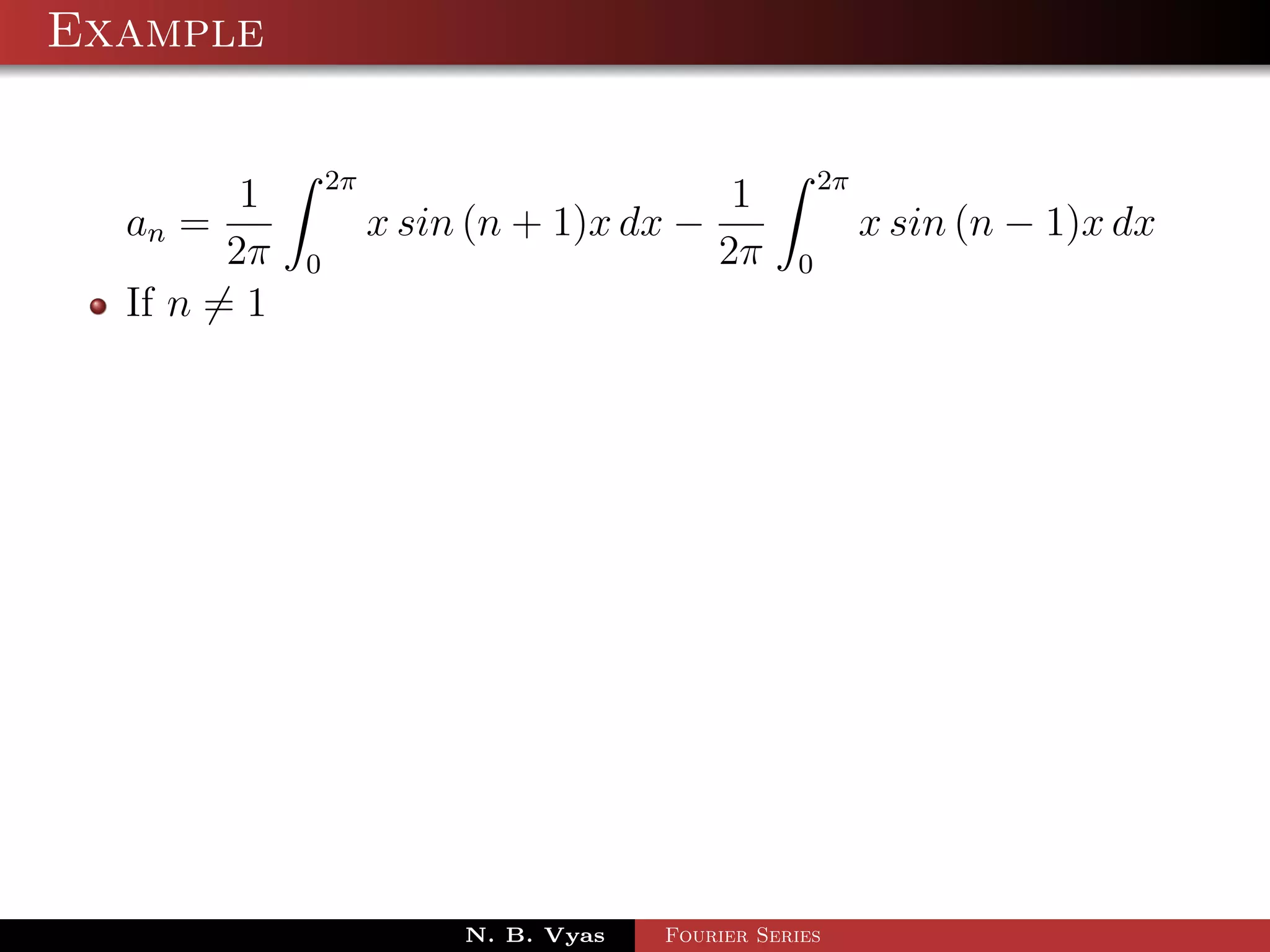
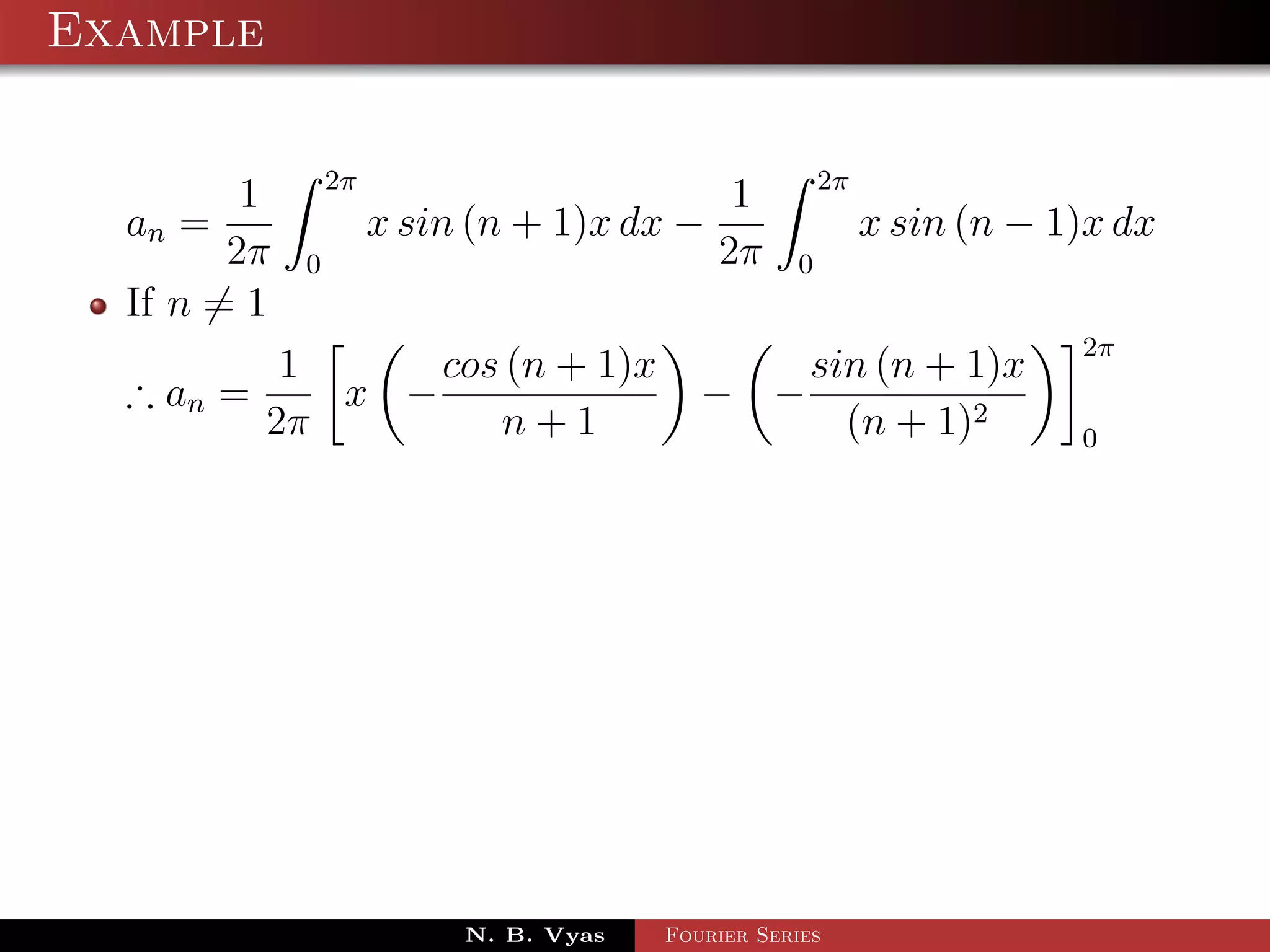
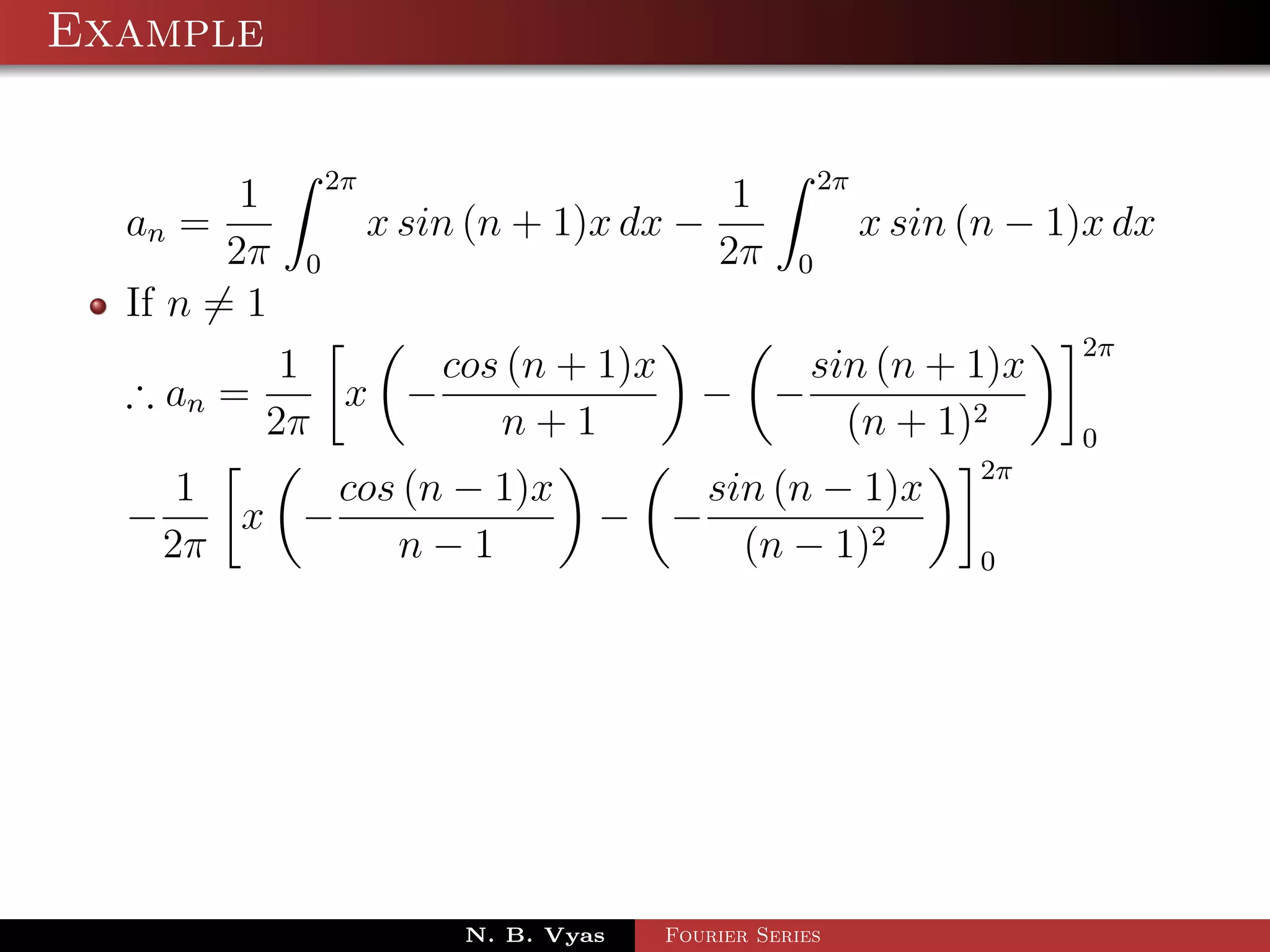
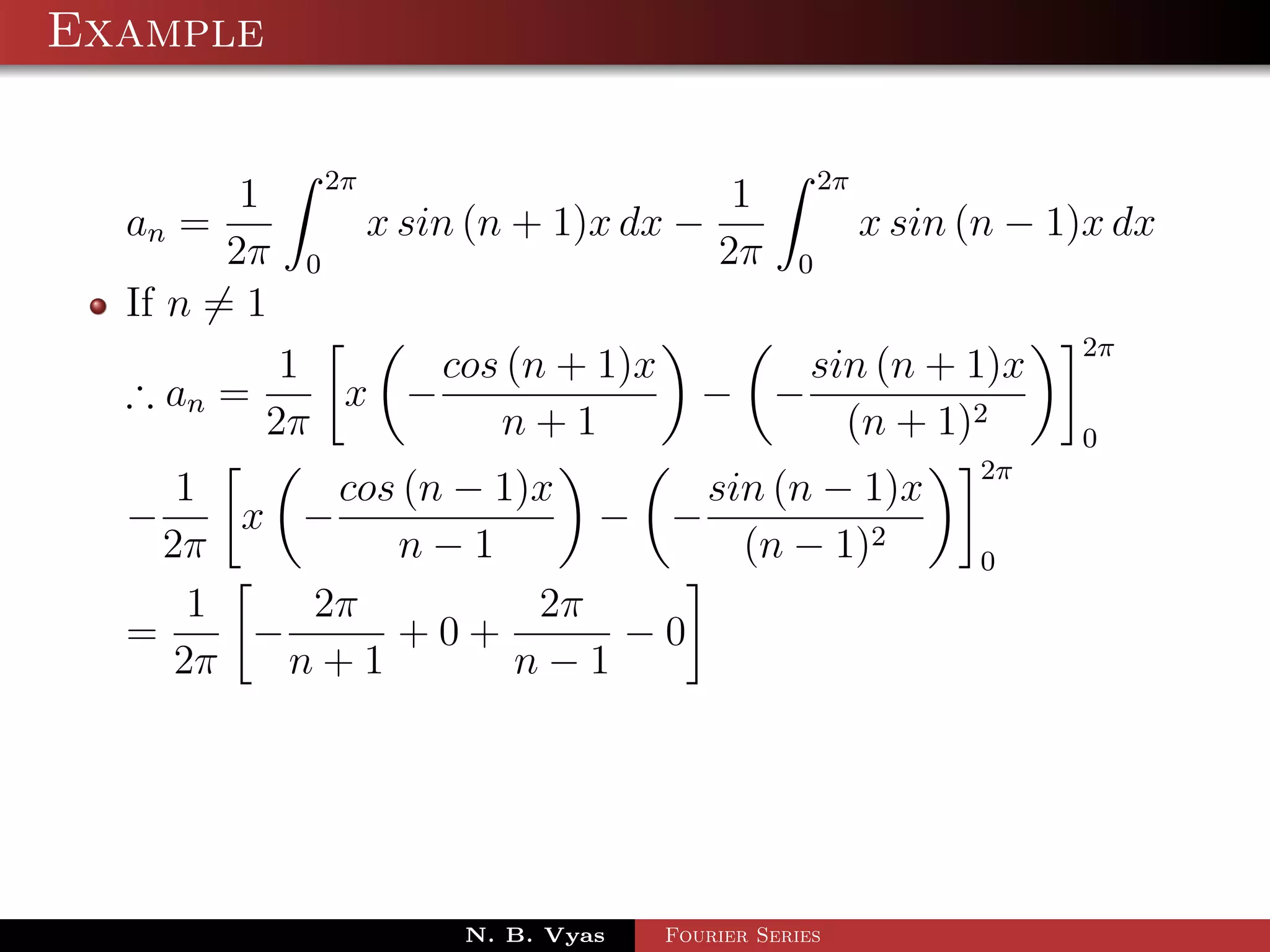
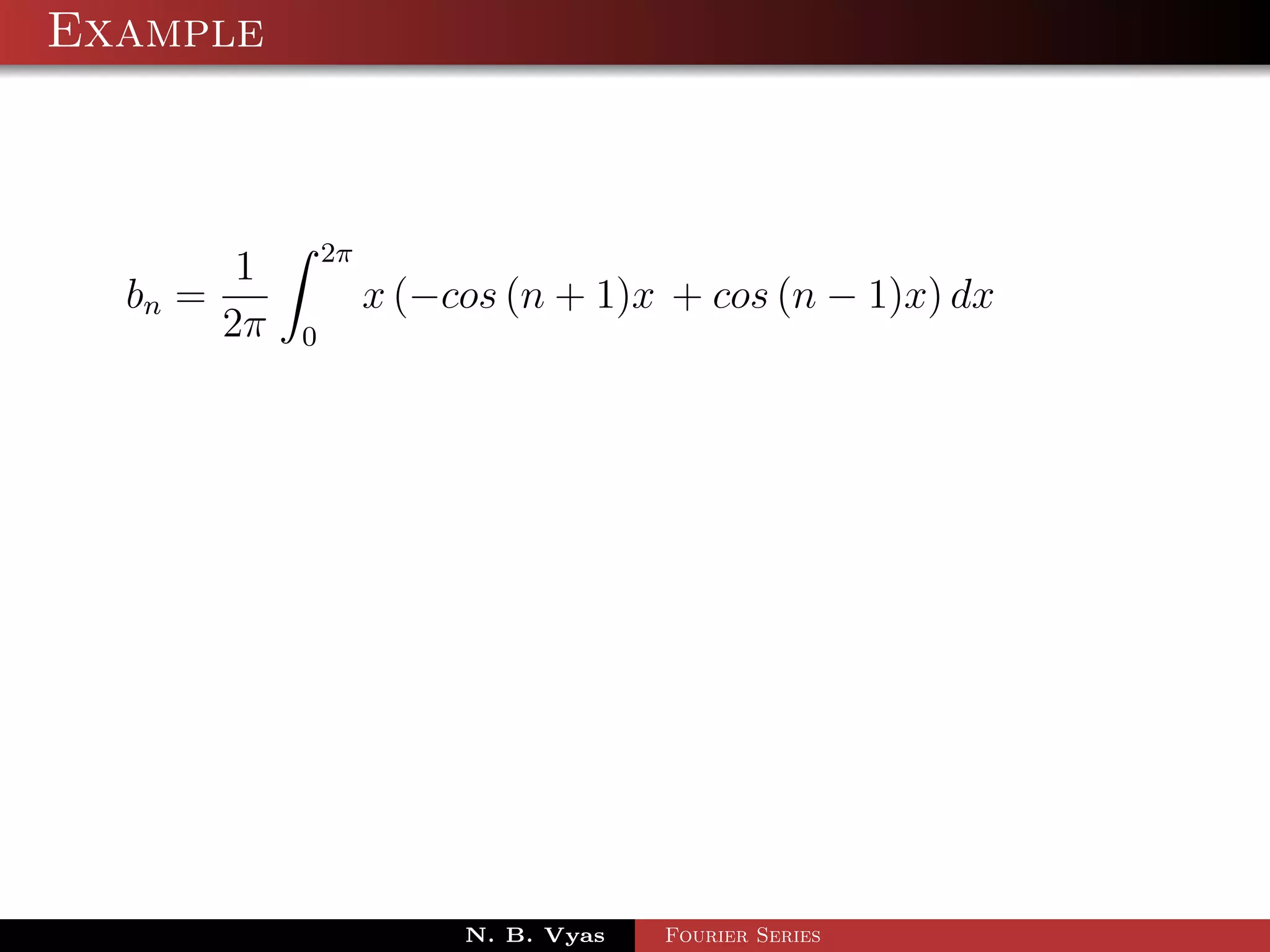
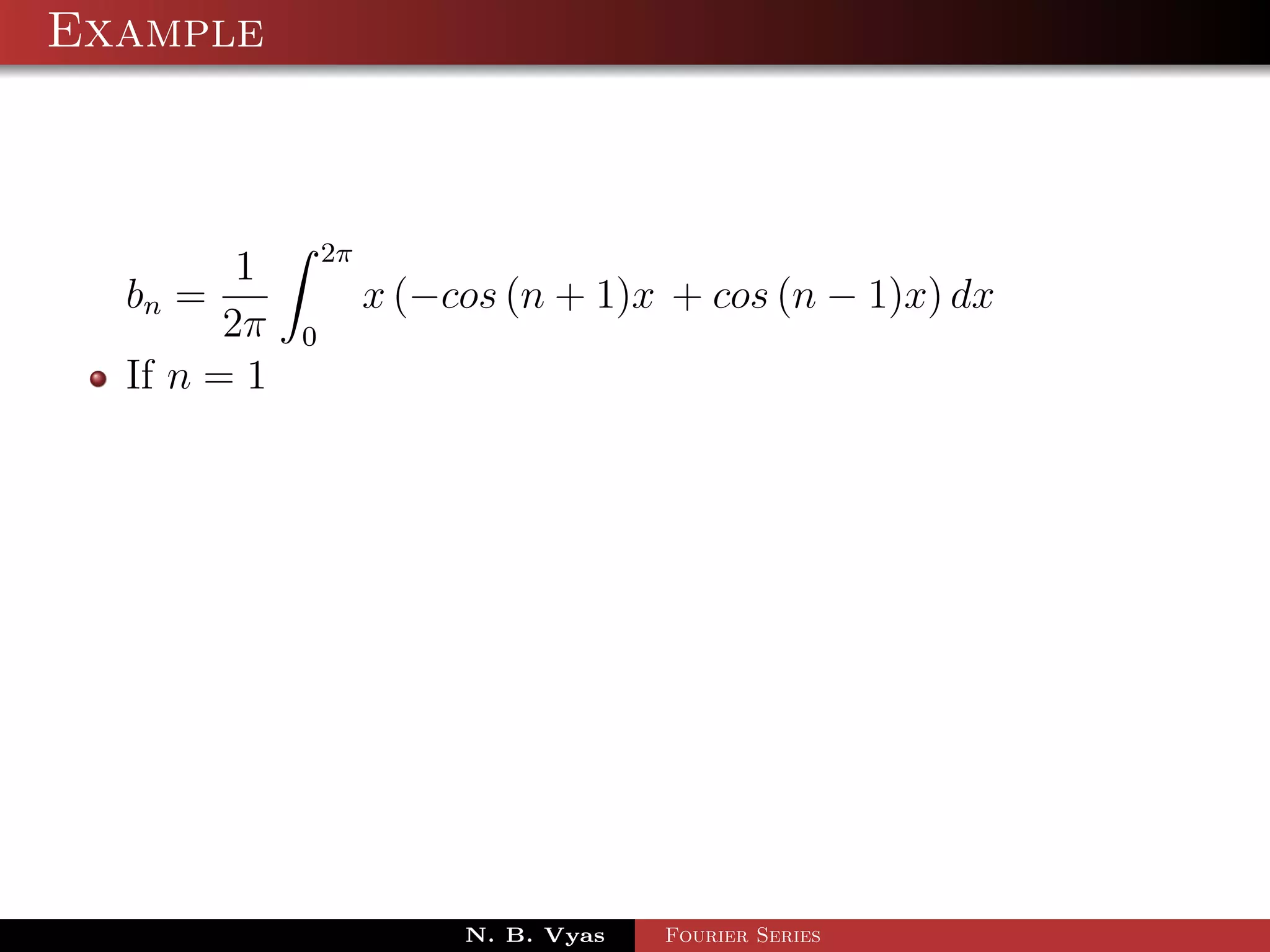
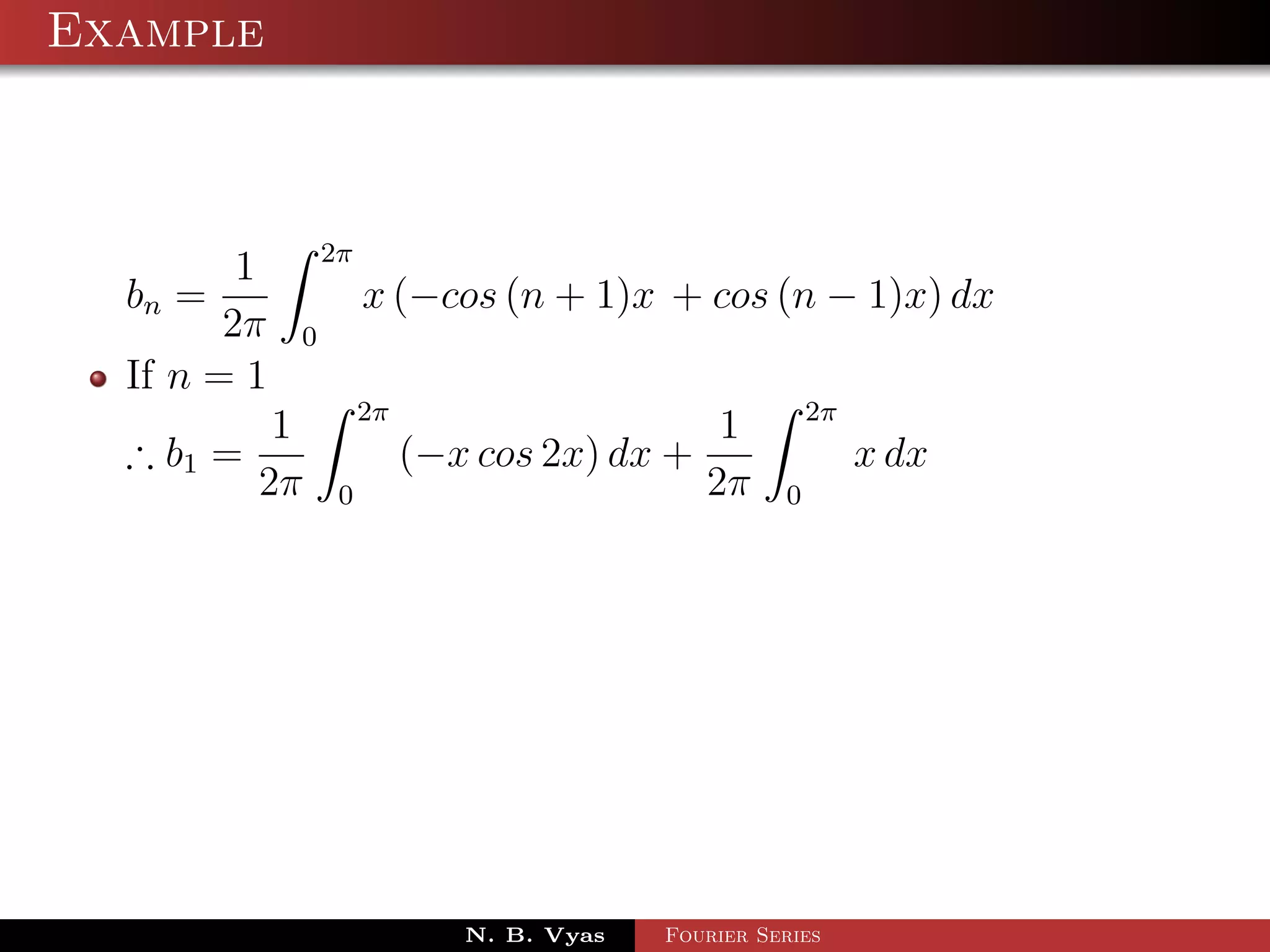
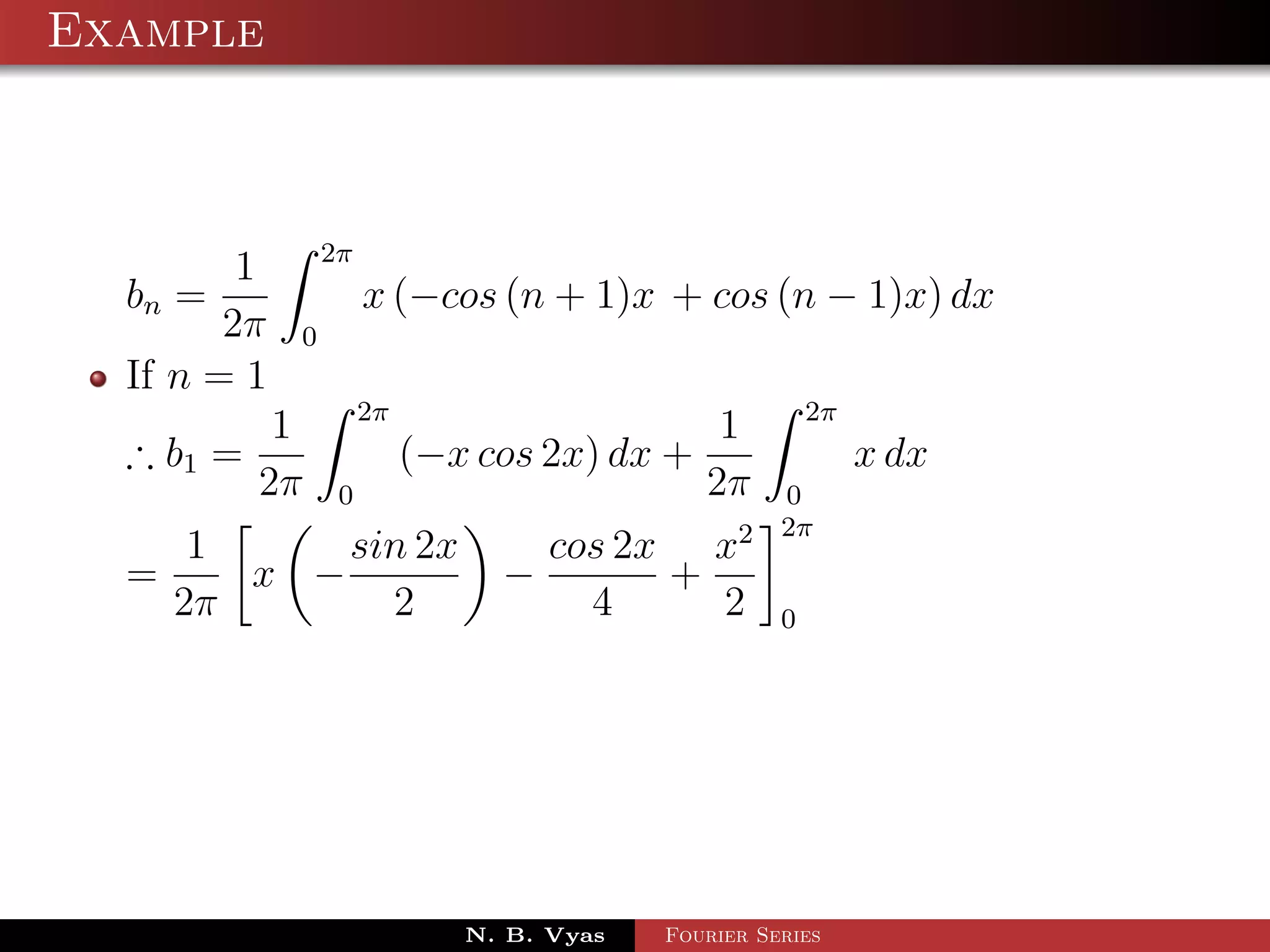
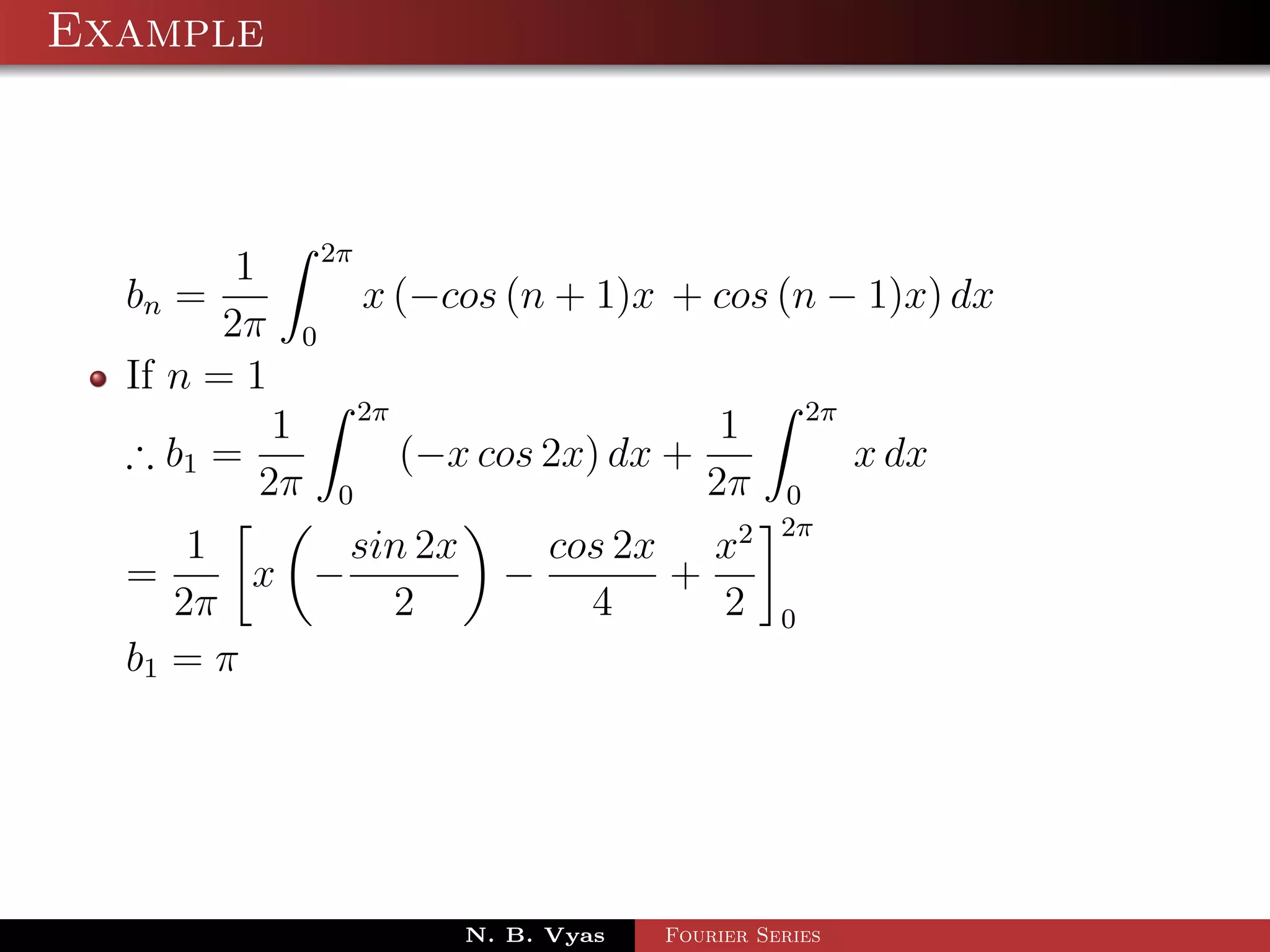
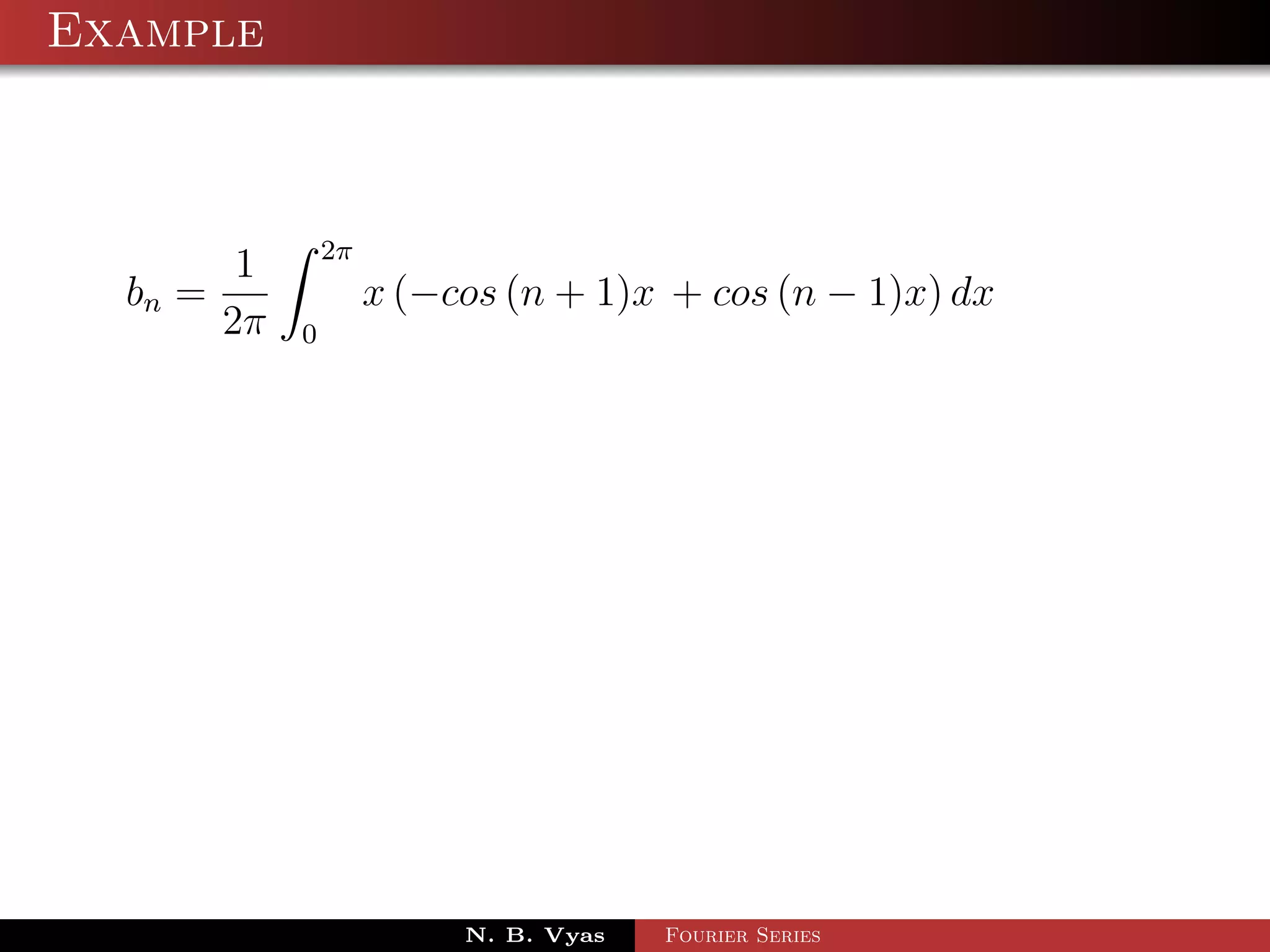
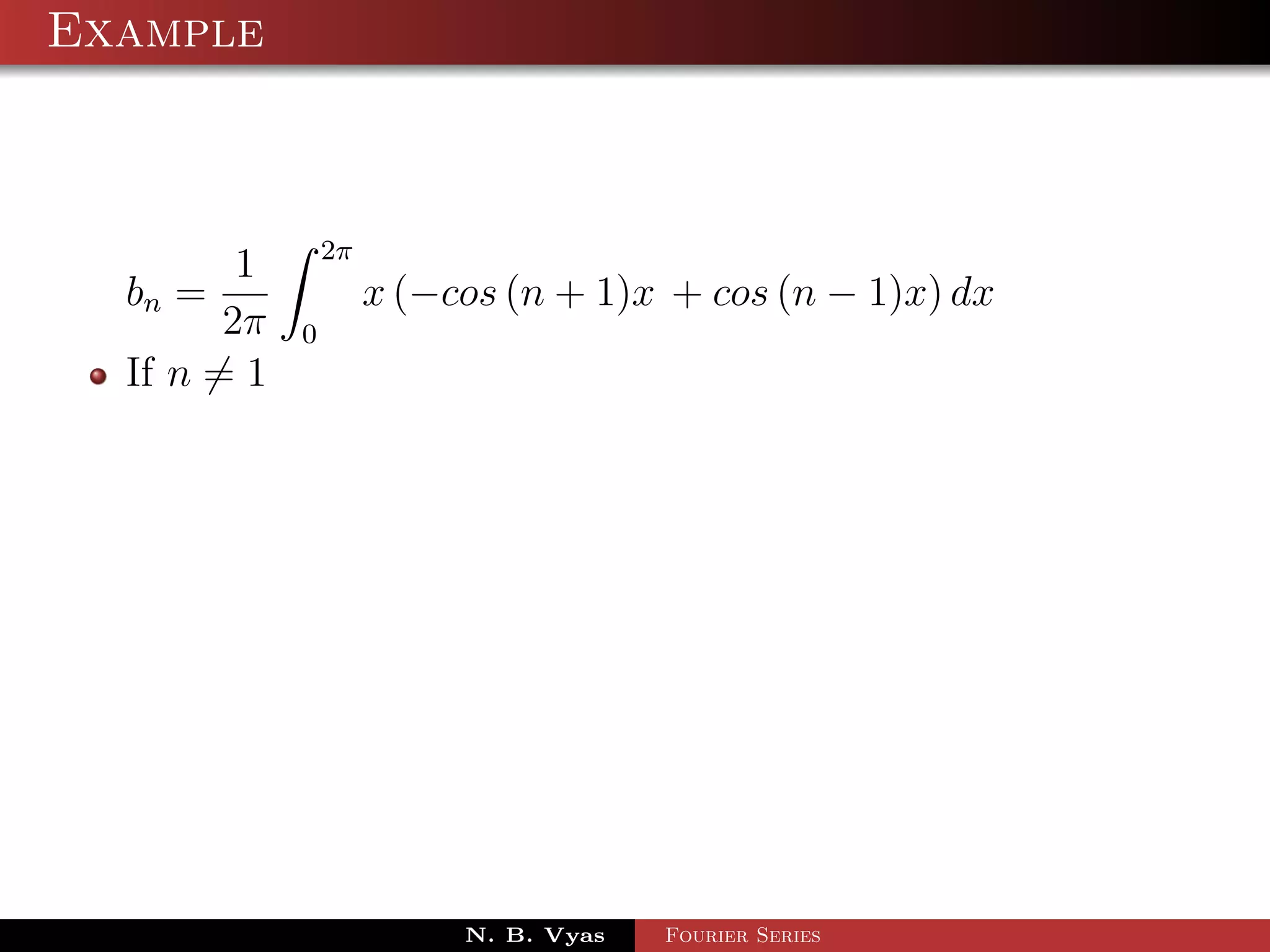
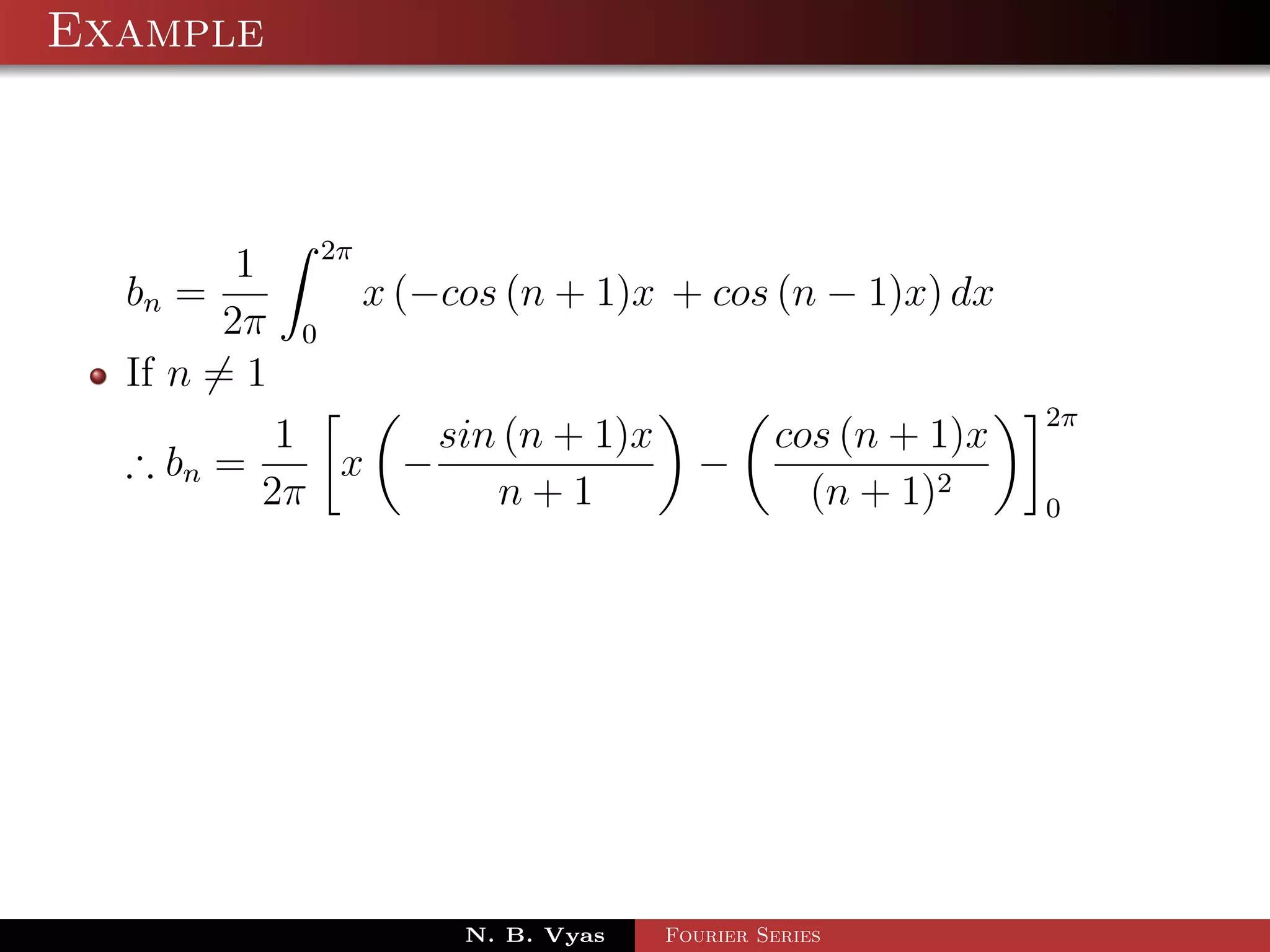
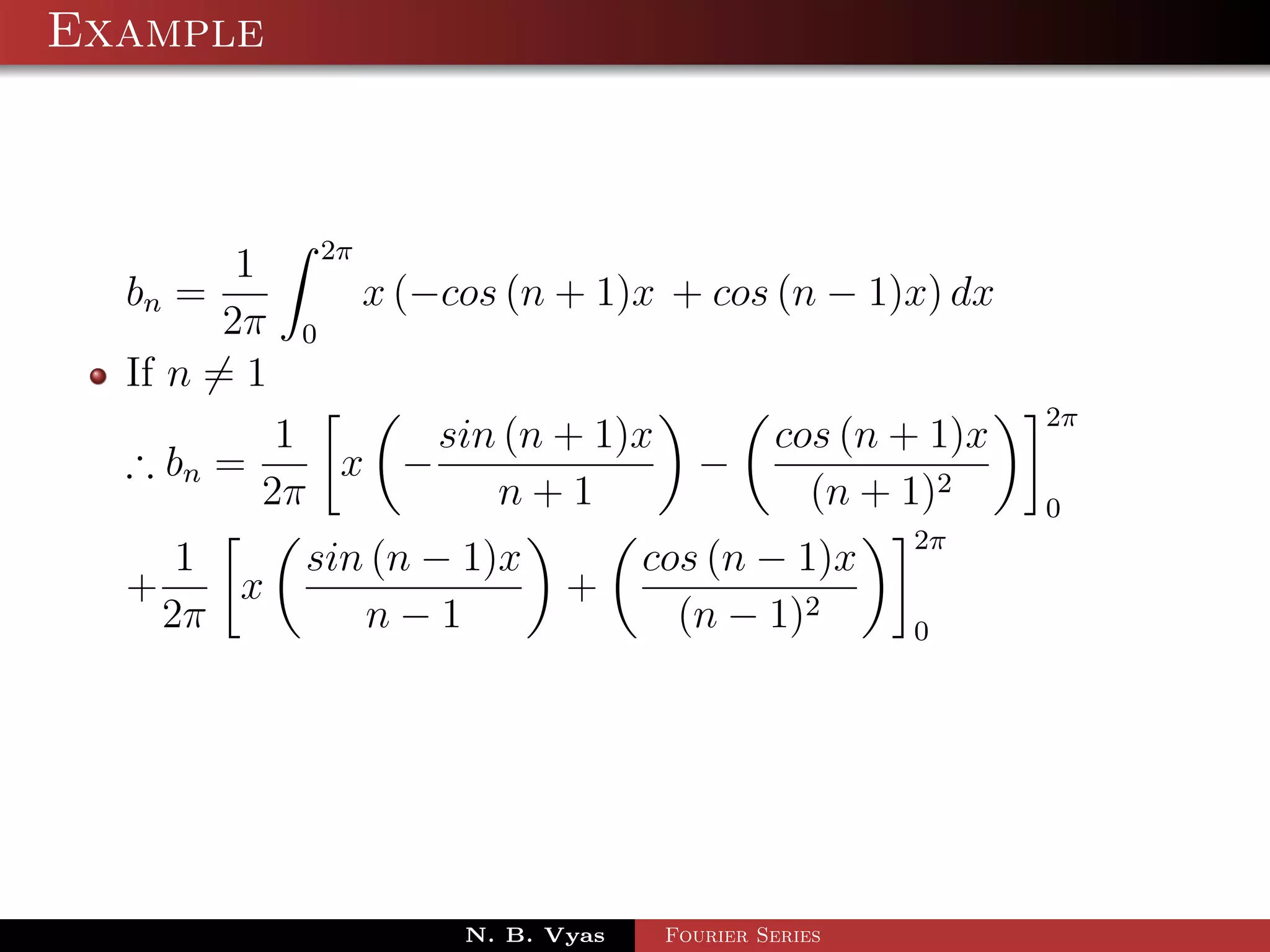
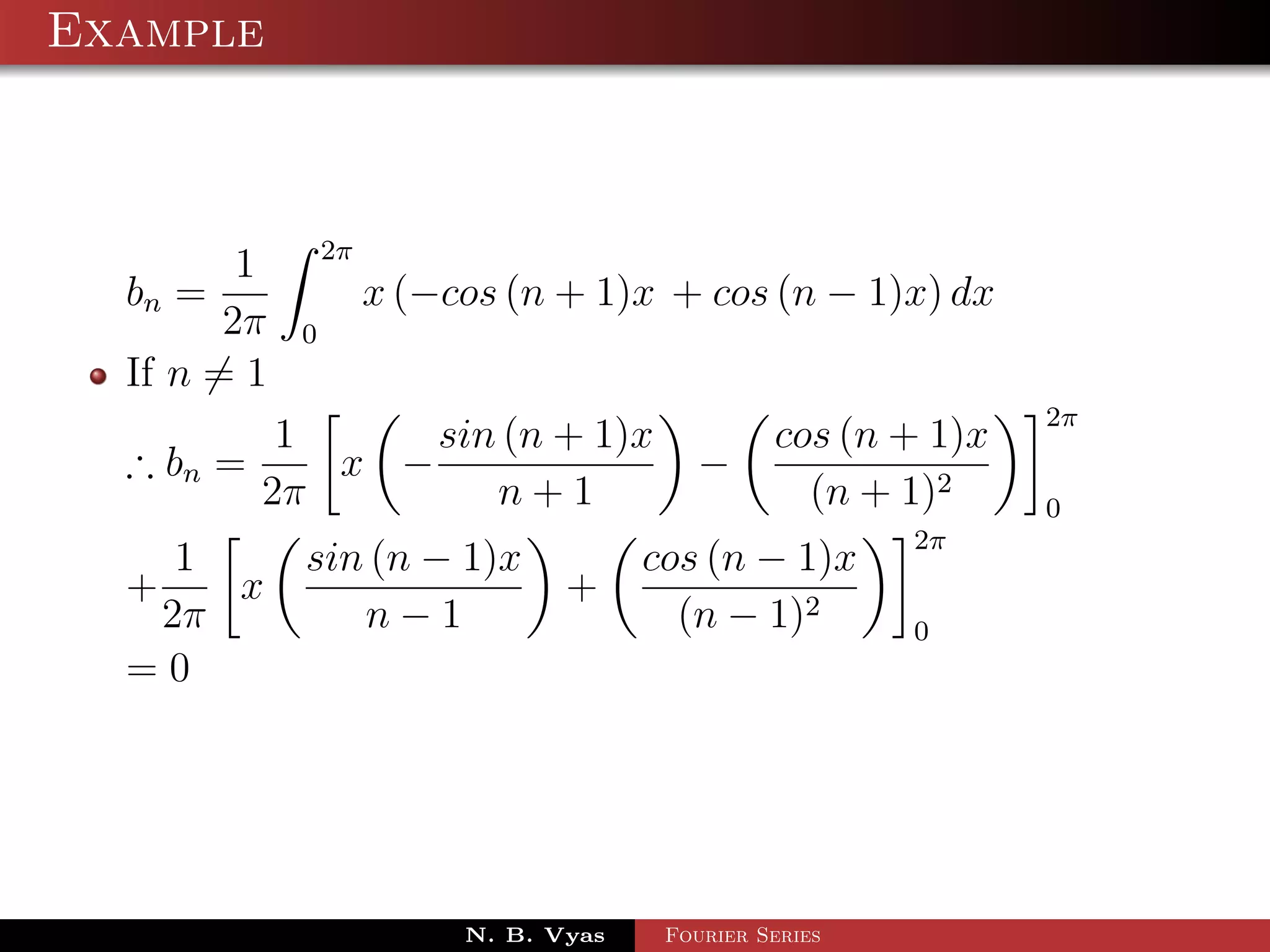
160. Example
Step 5. Substituting values of a0 , a1 , an (n > 1), b1 and
bn (n > 1) in (1), we get the required Fourier series of f (x) in
the interval [0, 2π]
N. B. Vyas Fourier Series

161. Example
Step 5. Substituting values of a0 , a1 , an (n > 1), b1 and
bn (n > 1) in (1), we get the required Fourier series of f (x) in
the interval [0, 2π]
∞
−2
f (x) = + (an cos nx + bn sin nx)
2 n=1
N. B. Vyas Fourier Series

162. Example
Step 5. Substituting values of a0 , a1 , an (n > 1), b1 and
bn (n > 1) in (1), we get the required Fourier series of f (x) in
the interval [0, 2π]
∞
−2
f (x) = + (an cos nx + bn sin nx)
2 n=1
N. B. Vyas Fourier Series

163. Example
Ex. Find the Fourier series for the periodic function
f (x)= −π; −π < x < 0
= x; 0 < x < π
N. B. Vyas Fourier Series

164. Example
Ex. Find the Fourier series for the periodic function
f (x)= −π; −π < x < 0
= x; 0 < x < π
N. B. Vyas Fourier Series

165. Example
Sol. Step 1. The Fourier series of f (x) is given by
N. B. Vyas Fourier Series

166. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
N. B. Vyas Fourier Series

167. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
π
1
where a0 = f (x) dx
π −π
N. B. Vyas Fourier Series

168. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
π
1
where a0 = f (x) dx
π −π
π
1
an = f (x) cos nx dx
π −π
N. B. Vyas Fourier Series

169. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
π
1
where a0 = f (x) dx
π −π
π
1
an = f (x) cos nx dx
π −π
π
1
bn = f (x) sin nx dx
π −π
N. B. Vyas Fourier Series

170. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
π
1
where a0 = f (x) dx
π −π
π
1
an = f (x) cos nx dx
π −π
π
1
bn = f (x) sin nx dx
π −π
N. B. Vyas Fourier Series

171. Example
π
1
Step 2. Now a0 = f (x) dx
π −π
N. B. Vyas Fourier Series

172. Example
π
1
Step 2. Now a0 = f (x) dx
π −π
0 π
1
= f (x) dx + f (x) dx
π −π 0
N. B. Vyas Fourier Series

173. Example
π
1
Step 2. Now a0 = f (x) dx
π −π
0 π
1
= f (x) dx + f (x) dx
π −π 0
0 π
1
= (−π) dx + x dx
π −π 0
N. B. Vyas Fourier Series

174. Example
π
1
Step 2. Now a0 = f (x) dx
π −π
0 π
1
= f (x) dx + f (x) dx
π −π 0
0 π
1
= (−π) dx + x dx
π −π 0
π
=−
2
N. B. Vyas Fourier Series

175. Example
π
1
Step 2. Now a0 = f (x) dx
π −π
0 π
1
= f (x) dx + f (x) dx
π −π 0
0 π
1
= (−π) dx + x dx
π −π 0
π
=−
2
N. B. Vyas Fourier Series

176. Example
0 π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π −π 0
N. B. Vyas Fourier Series

177. Example
1 0 π
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π −π 0
0 π
1
= (−π) cos nx dx + x cos nx dx
π −π 0
N. B. Vyas Fourier Series

178. Example
1 0 π
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π −π 0
0 π
1
= (−π) cos nx dx + x cos nx dx
π −π 0
0
1 sin nx
= −π +
π n −π
N. B. Vyas Fourier Series

179. Example
1 0 π
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π −π 0
0 π
1
= (−π) cos nx dx + x cos nx dx
π −π 0
0 π
1 sin nx sin nx cos nx
= −π + x − (1) −
π n −π n n2 0
N. B. Vyas Fourier Series

180. Example
1 0 π
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π −π 0
0 π
1
= (−π) cos nx dx + x cos nx dx
π −π 0
0 π
1 sin nx sin nx cos nx
= −π + x − (1) −
π n −π n n2 0
n
(−1) − 1
=
πn2
N. B. Vyas Fourier Series

181. Example
0 π
1
Step 4. bn = f (x) sin nx dx + f (x) sin nx dx
π −π 0
N. B. Vyas Fourier Series

182. Example
0 π
1
Step 4. bn = f (x) sin nx dx + f (x) sin nx dx
π −π 0
0 π
1
= (−π) sin nx dx + x sin nx dx
π −π 0
N. B. Vyas Fourier Series

183. Example
0 π
1
Step 4. bn = f (x) sin nx dx + f (x) sin nx dx
π −π 0
0 π
1
= (−π) sin nx dx + x sin nx dx
π −π 0
0
1 −cosnx
= −π +
π n −π
N. B. Vyas Fourier Series

184. Example
0 π
1
Step 4. bn = f (x) sin nx dx + f (x) sin nx dx
π −π 0
0 π
1
= (−π) sin nx dx + x sin nx dx
π −π 0
0 π
1 −cosnx −cos nx −sin nx
= −π + x −
π n −π n n2 0
N. B. Vyas Fourier Series

185. Example
0 π
1
Step 4. bn = f (x) sin nx dx + f (x) sin nx dx
π −π 0
0 π
1
= (−π) sin nx dx + x sin nx dx
π −π 0
0 π
1 −cosnx −cos nx −sin nx
= −π + x −
π n −π n n2 0
n
1 − 2(−1)
=
n
N. B. Vyas Fourier Series

186. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval (−π, π)
N. B. Vyas Fourier Series

187. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval (−π, π)
∞
−π
f (x) = + (an cos nx + bn sin nx)
4 n=1
N. B. Vyas Fourier Series

188. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval (−π, π)
∞
−π
f (x) = + (an cos nx + bn sin nx)
4 n=1
∞ ∞
−π (−1)n − 1 1 − 2(−1)n
= + cos nx + sin nx
4 n=1
πn2 n=1
n
N. B. Vyas Fourier Series

189. Example
Step 5. Substituting values of a0 , an and bn in (1), we get the
required Fourier series of f (x) in the interval (−π, π)
∞
−π
f (x) = + (an cos nx + bn sin nx)
4 n=1
∞ ∞
−π (−1)n − 1 1 − 2(−1)n
= + cos nx + sin nx
4 n=1
πn2 n=1
n
N. B. Vyas Fourier Series

190. Example
Ex. Find the Fourier series for the periodic function
f (x)= 2; −π < x < 0
= 1; 0 < x < π
N. B. Vyas Fourier Series

191. Example
Ex. Find the Fourier series for the periodic function
f (x)= 2; −π < x < 0
= 1; 0 < x < π
N. B. Vyas Fourier Series

192. Example
Ex. Find the Fourier series for the periodic function
f (x)= −k; −π < x < 0
= k; 0 < x < π
N. B. Vyas Fourier Series

193. Example
Ex. Find the Fourier series for the periodic function
f (x)= −k; −π < x < 0
= k; 0 < x < π
1 1 1 π
Hence deduce that 1 − + − + . . . =
3 5 7 4
N. B. Vyas Fourier Series

194. Example
Ex. Find the Fourier series of the function
f (x)= x; 0 ≤ x < π
= 2π ; x = π
= 2π − x ; π < x < 2π
3π 2 1 1 1
Hence deduce that = 2 + 2 + 2 + ...
8 1 3 5
N. B. Vyas Fourier Series

195. Example
Sol. Step 1. The Fourier series of f (x) is given by
N. B. Vyas Fourier Series

196. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
N. B. Vyas Fourier Series

197. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

198. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
π
1
an = f (x) cos nx dx
π 0
N. B. Vyas Fourier Series

199. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

200. Example
Sol. Step 1. The Fourier series of f (x) is given by
∞
a0
f (x) = + (an cos nx + bn sin nx) . . . (1)
2 n=1
2π
1
where a0 = f (x) dx
π 0
π
1
an = f (x) cos nx dx
π 0
2π
1
bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

201. Example
2π
1
Step 2. Now a0 = f (x) dx
π 0
N. B. Vyas Fourier Series

202. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
π 2π
1
= x dx + (2π − x) dx
π 0 π
N. B. Vyas Fourier Series

203. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
π 2π
1
= x dx + (2π − x) dx
π 0 π
π 2π
1 x2 x2
= + 2πx −
π 2 0 2 π
N. B. Vyas Fourier Series

204. Example
1 2π
Step 2. Now a0 = f (x) dx
π 0
π 2π
1
= x dx + (2π − x) dx
π 0 π
π 2π
1 x2 x2
= + 2πx −
π 2 0 2 π
=π
N. B. Vyas Fourier Series

205. Example
π 2π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π 0 π
N. B. Vyas Fourier Series

206. Example
π 2π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π 0 π
π 2π
1
= x cos nx dx + (2π − x) cos nx dx
π 0 π
N. B. Vyas Fourier Series

207. Example
π 2π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π 0 π
π 2π
1
= x cos nx dx + (2π − x) cos nx dx
π 0 π
π
1 sin nx cos nx
= x − (1) −
π n n2 0
N. B. Vyas Fourier Series

208. Example
π 2π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π 0 π
π 2π
1
= x cos nx dx + (2π − x) cos nx dx
π 0 π
π
1 sin nx cos nx
= x − (1) −
π n n2 0
2π
1 sin nx cos nx
+ (2π − x) − (−1) −
π n n2 π
N. B. Vyas Fourier Series

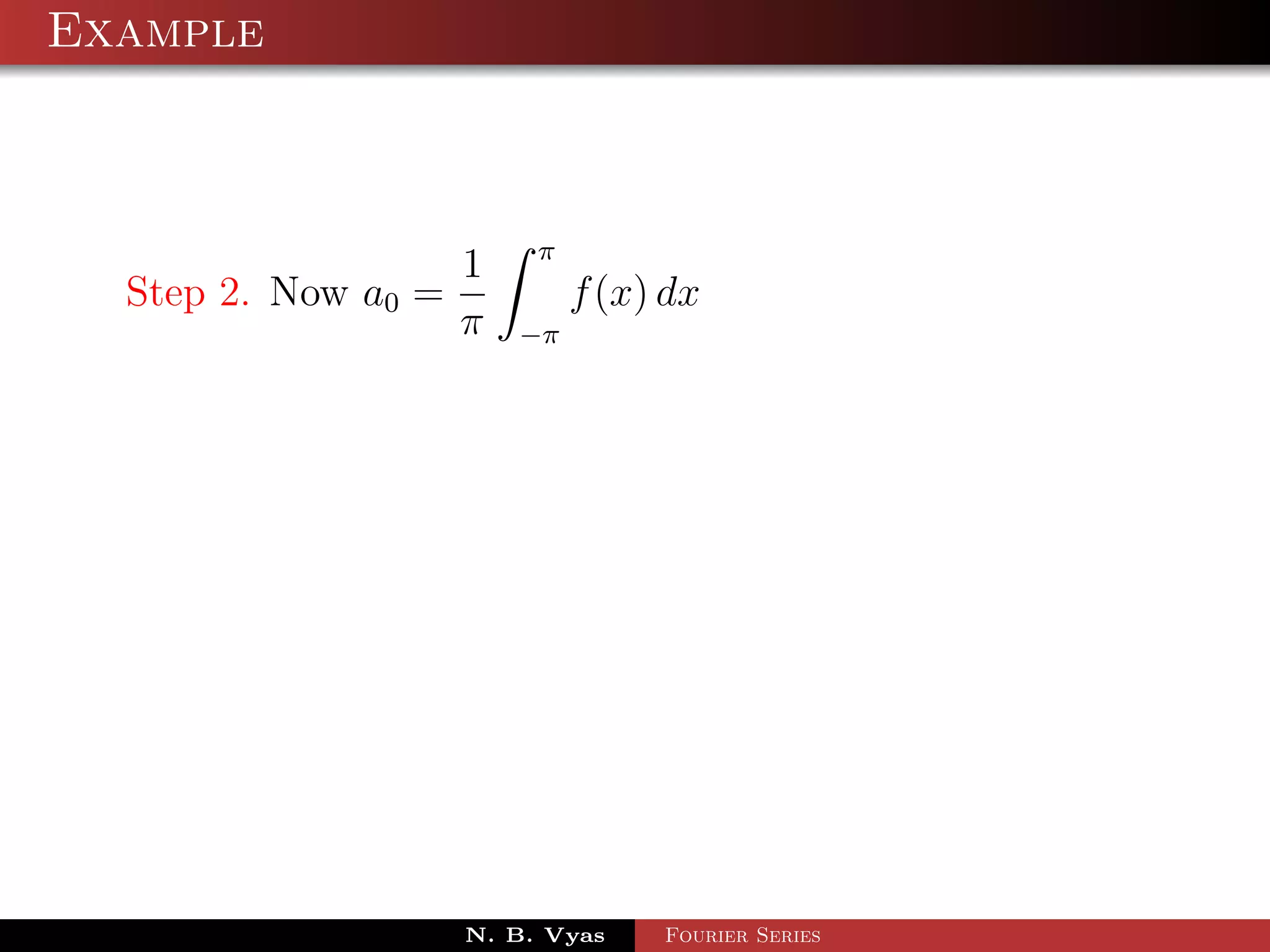
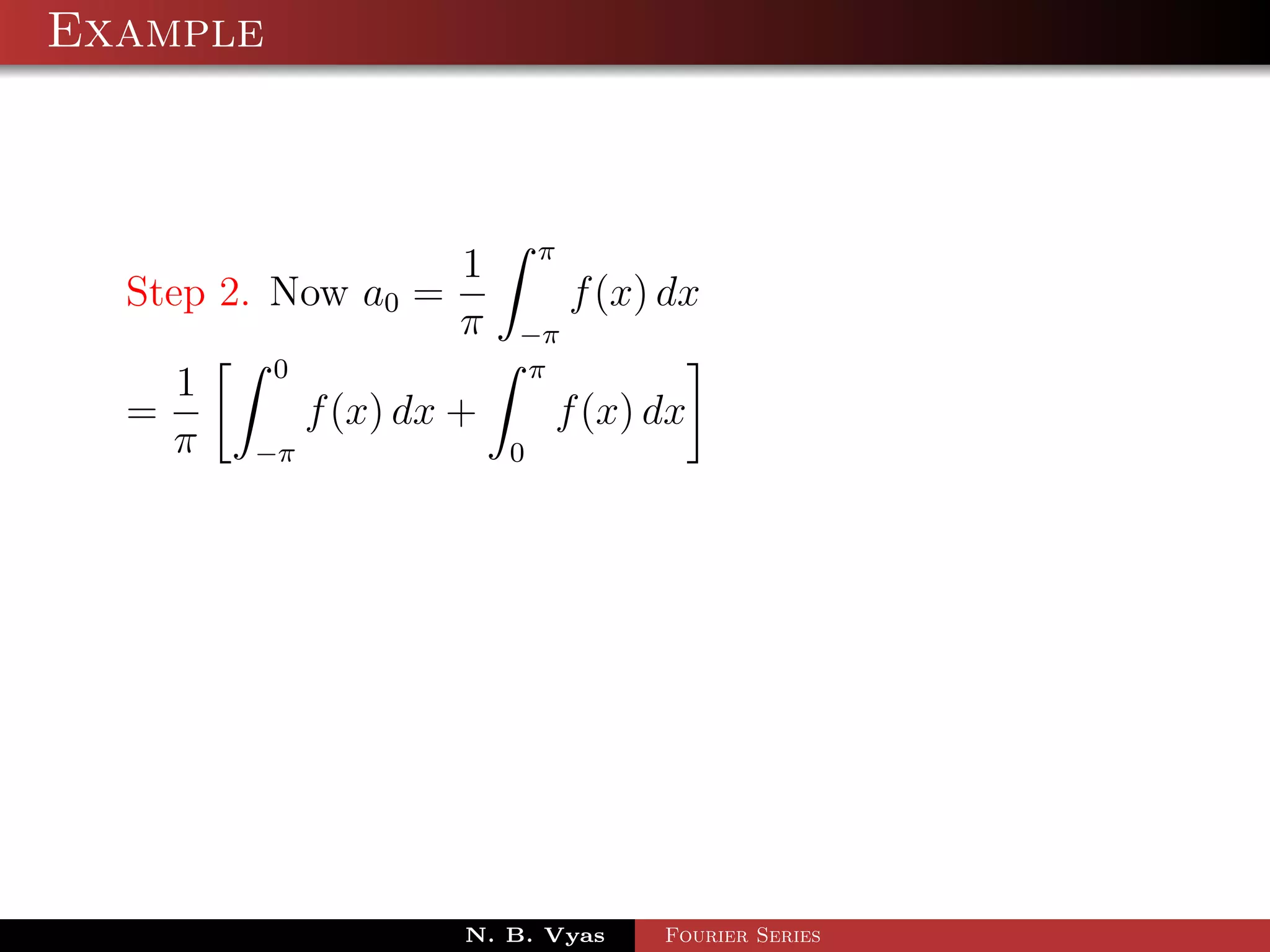
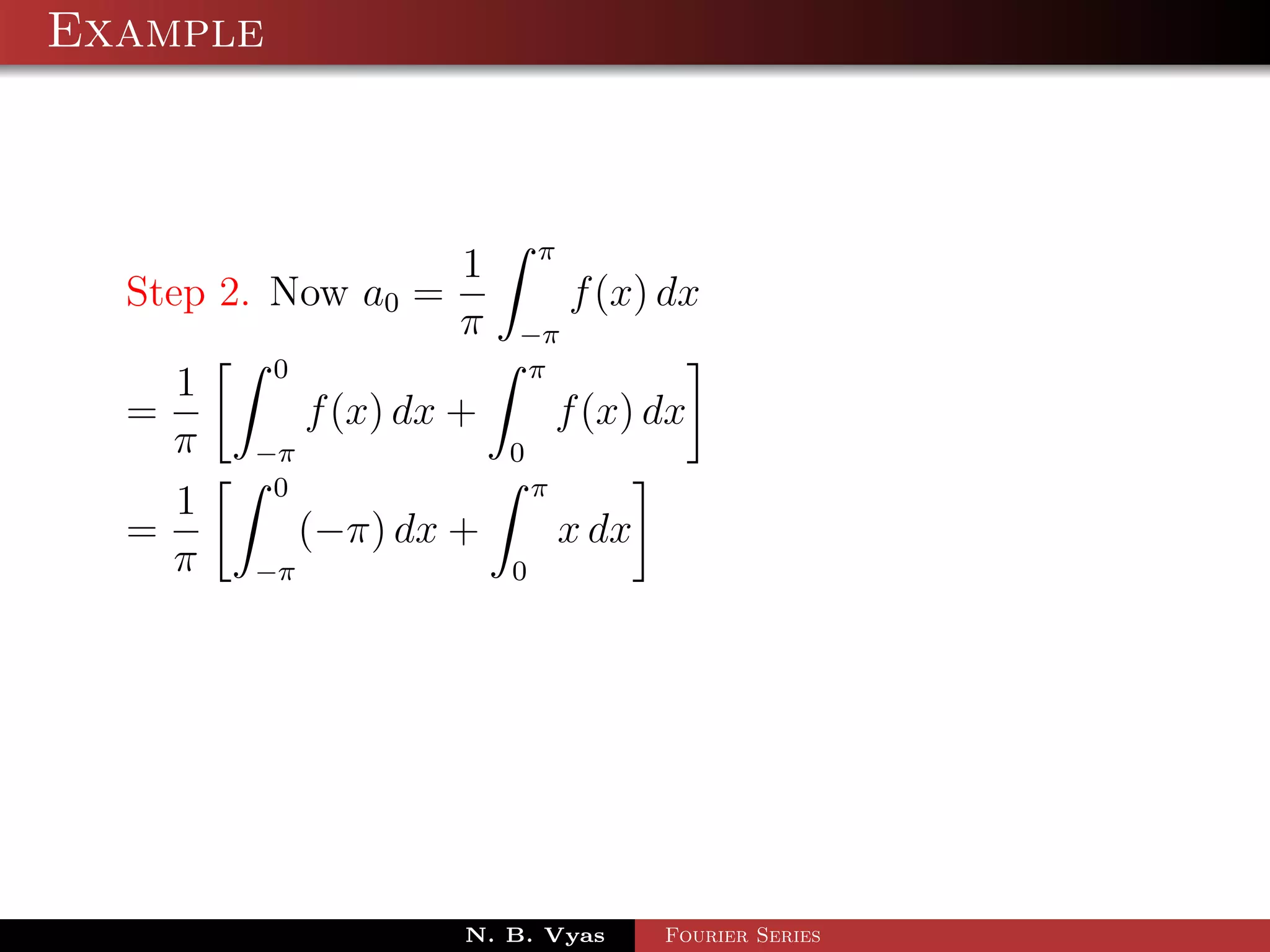
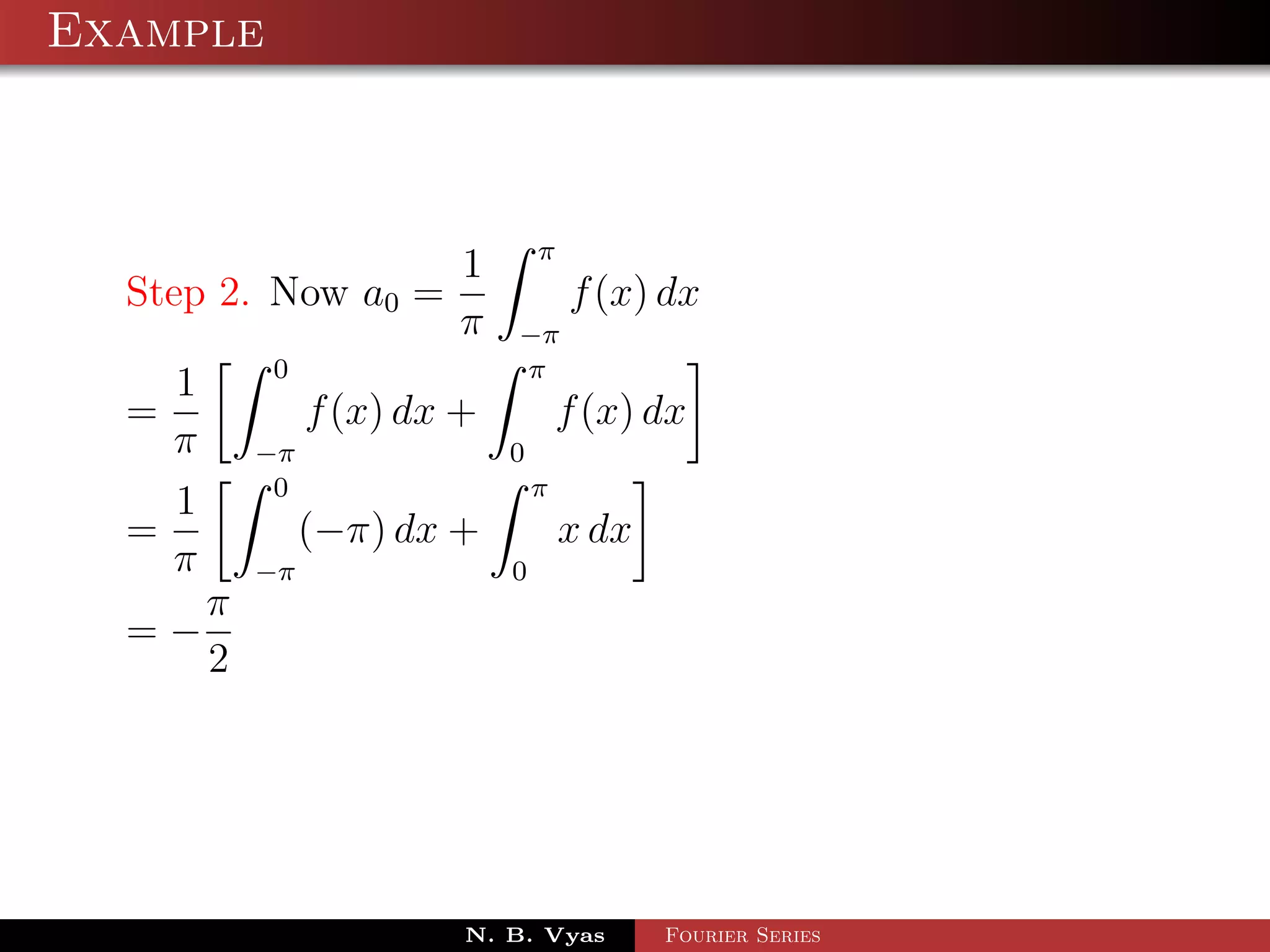
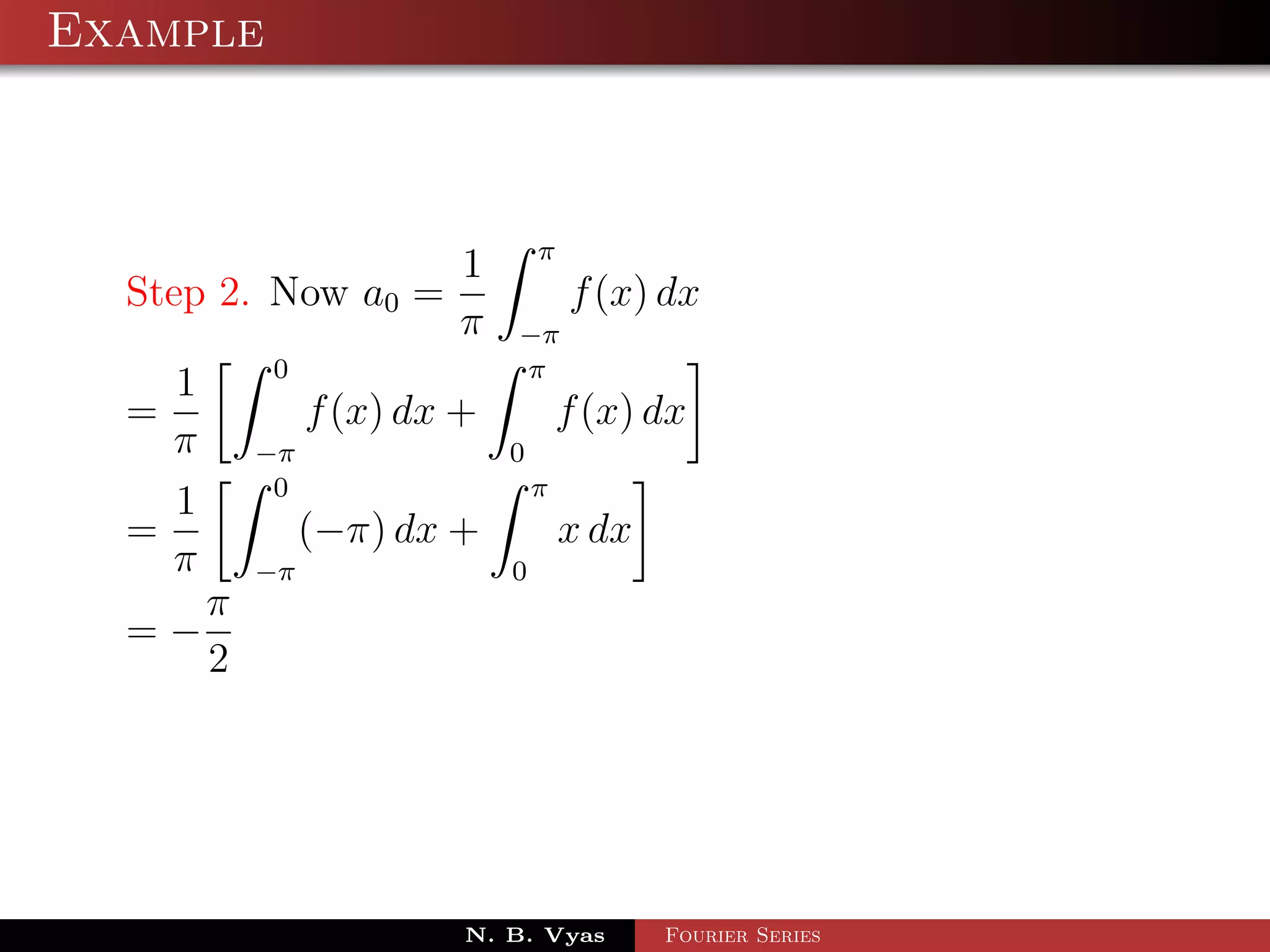
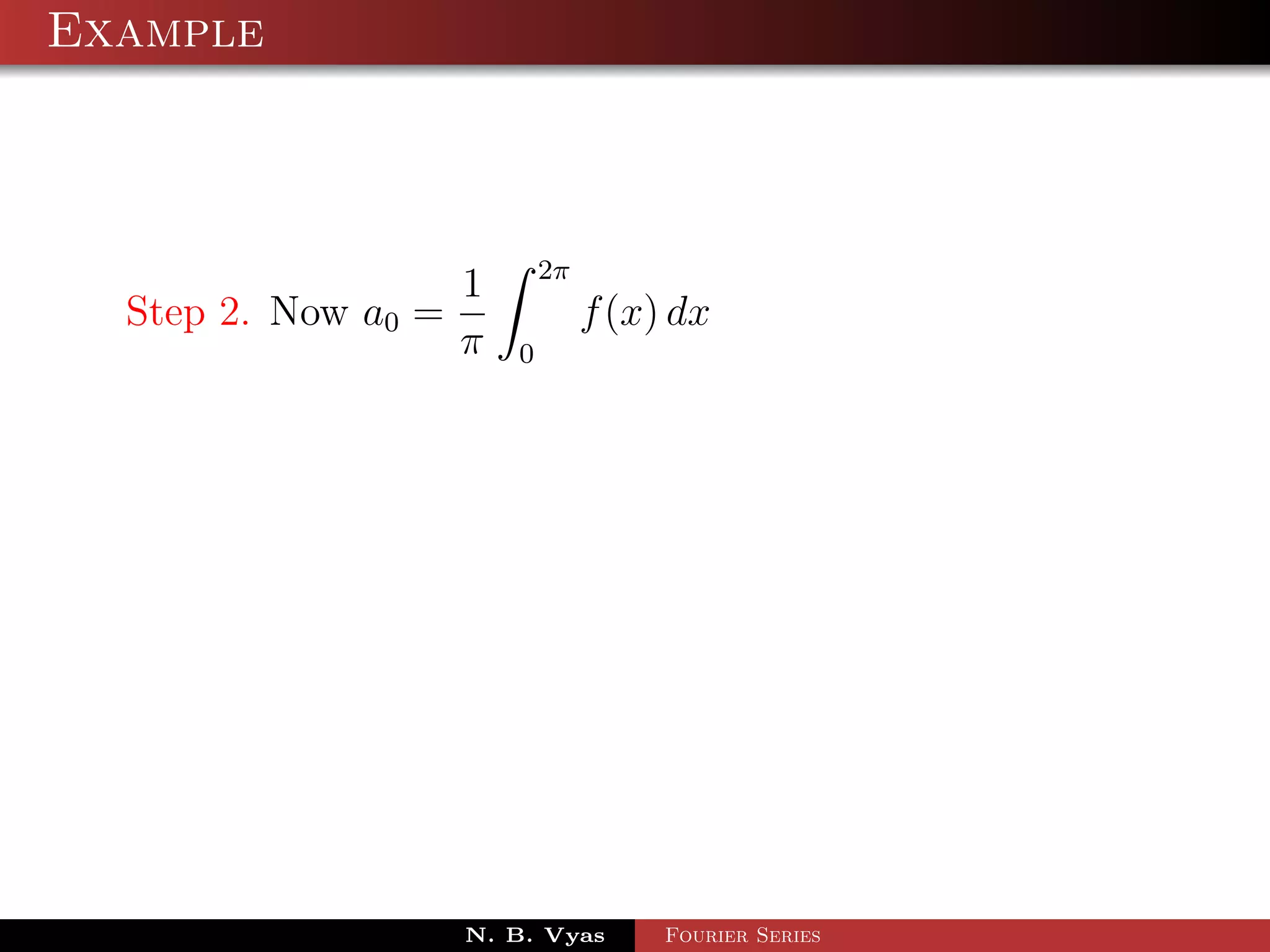
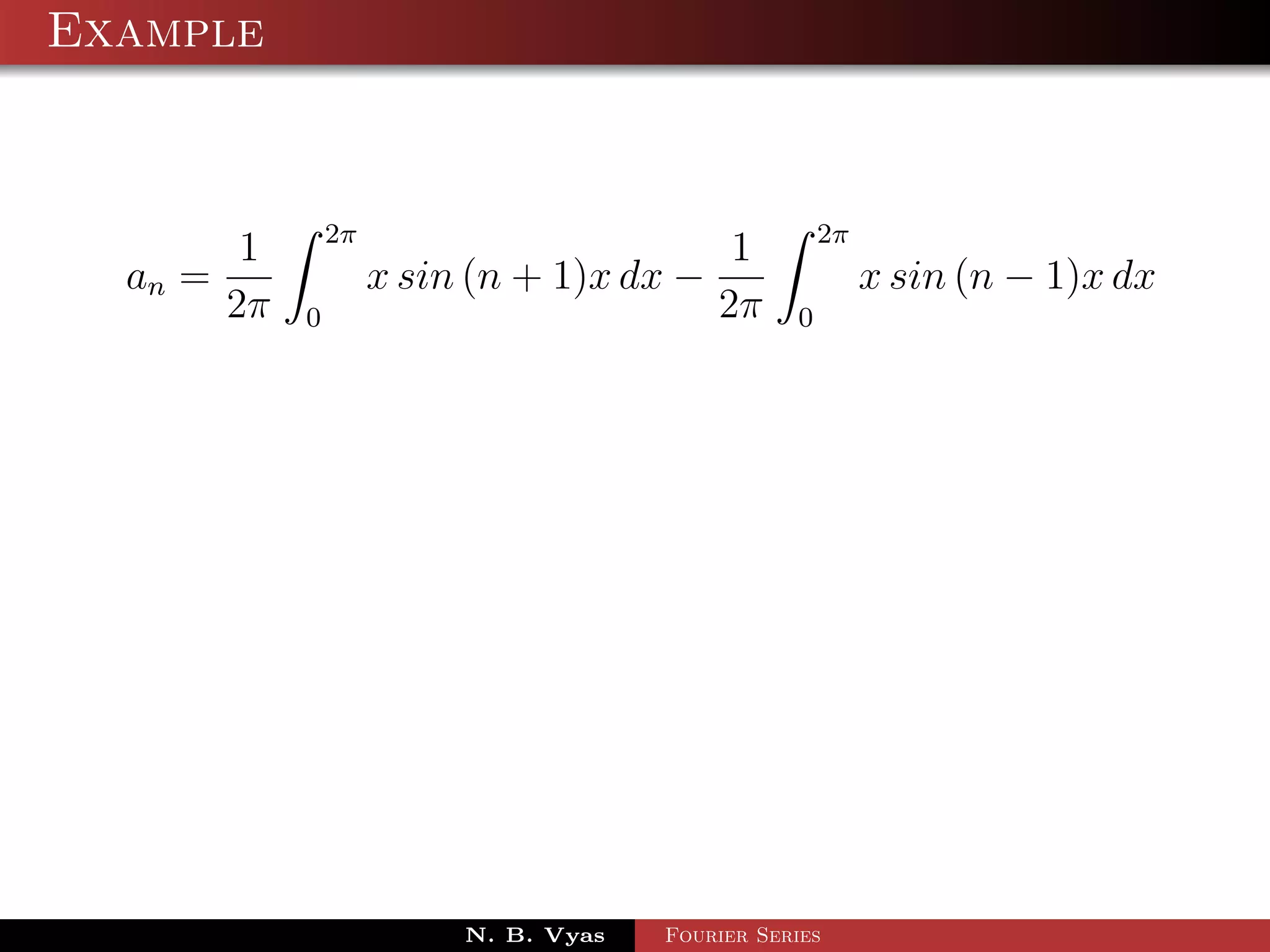
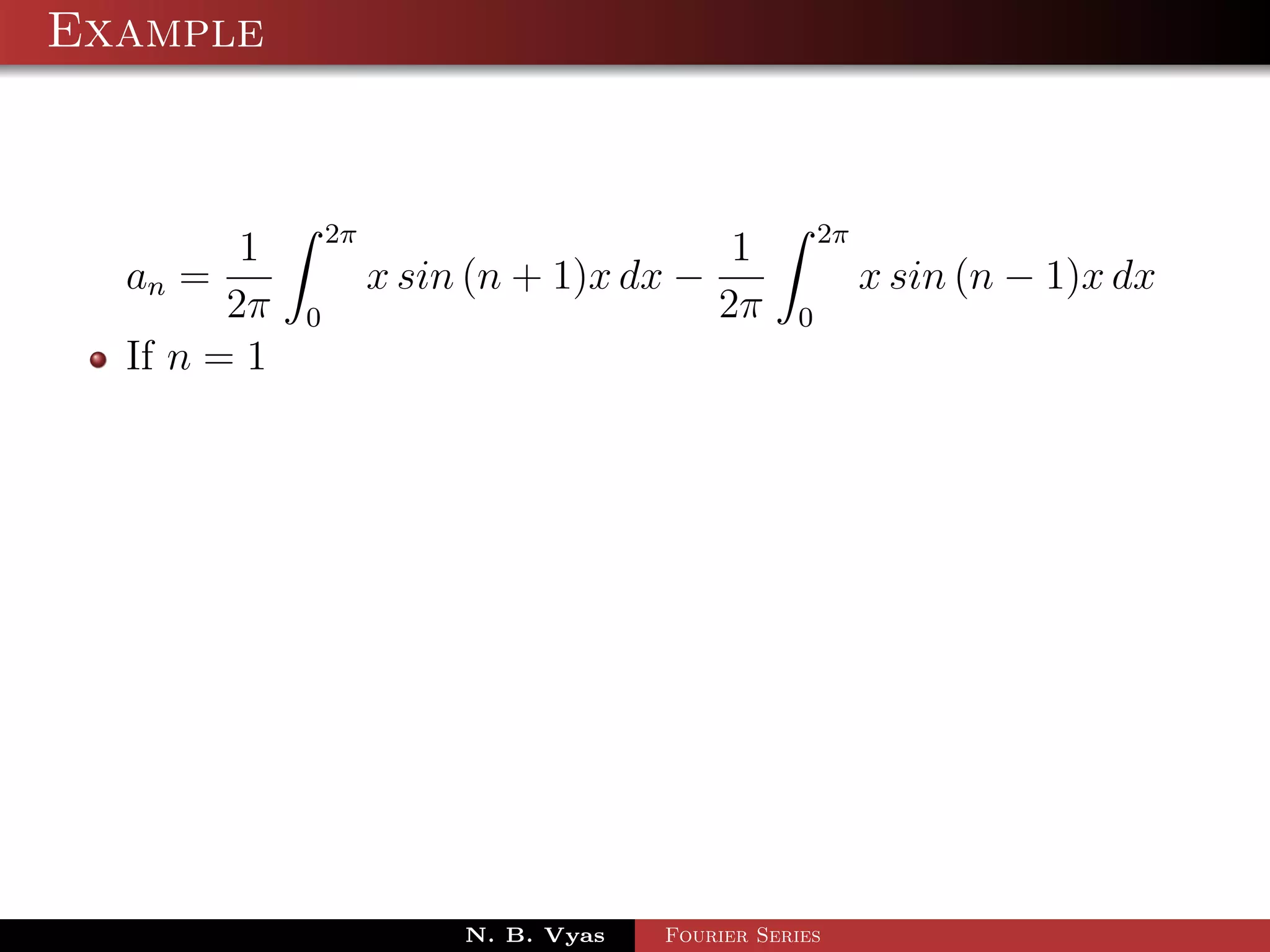
209. Example
π 2π
1
Step 3. an = f (x) cos nx dx + f (x) cos nx dx
π 0 π
π 2π
1
= x cos nx dx + (2π − x) cos nx dx
π 0 π
π
1 sin nx cos nx
= x − (1) −
π n n2 0
2π
1 sin nx cos nx
+ (2π − x) − (−1) −
π n n2 π
1 cos nπ 1
= 0+ 2
− 0+ 2
π n n
1 cos 2nπ cos nπ
+ 0− 2
− 0−
π n n2
2 [(−1)n − 1]
=
πn2
N. B. Vyas Fourier Series

210. Example
2π
1
Step 4. bn = f (x) sin nx dx
π 0
N. B. Vyas Fourier Series

211. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
π 2π
1
= x sin nx dx + (2π − x) sin nx dx
π 0 π
N. B. Vyas Fourier Series

212. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
π 2π
1
= x sin nx dx + (2π − x) sin nx dx
π 0 π
π
1 cos nx sin nx
= x − − (1) −
π n n2 0
N. B. Vyas Fourier Series

213. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
π 2π
1
= x sin nx dx + (2π − x) sin nx dx
π 0 π
π
1 cos nx sin nx
= x − − (1) −
π n n2 0
2π
1 cos nx sin nx
+ (2π − x) − − (−1) −
π n n2 π
N. B. Vyas Fourier Series

214. Example
1 2π
Step 4. bn = f (x) sin nx dx
π 0
π 2π
1
= x sin nx dx + (2π − x) sin nx dx
π 0 π
π
1 cos nx sin nx
= x − − (1) −
π n n2 0
2π
1 cos nx sin nx
+ (2π − x) − − (−1) −
π n n2 π
=0
N. B. Vyas Fourier Series

215. Example
Ex. Find the Fourier series of
f (x)= −1; −π < x < − π 2
= 0 ; −π < x < π
2 2
= 1; π < x < π
2
N. B. Vyas Fourier Series