This document discusses numerical methods for solving nonlinear equations. It describes two types of methods - bracket/close methods which include bisection and false position, and open methods which include fixed point iteration and Newton-Raphson. For each method, it provides the algorithm, works through an example problem, and discusses advantages and disadvantages. The document was presented by three students at North Western University, Khulna on the topic of numerical methods for solving nonlinear equations.

1. North Western University, Khulna
Numerical Analysis
Course code : EEE -2307
Presentation Topic :Presentation Topic :
Numerical method for solving
Non-linear equations
Presented by :
20183025021- Md. Milan Molla
20183026021- Md. Mozammel Haque
20183029021- Madan Mohon Debnath

2. What is Non-linear equations?
If the power of independent variable is more than
one, it is called non-linear equation. Trigonometric functions (like
sine or cosine) are non-linear. Square roots are non-linear,
y=xcosx+(x^2)tanx
Types of Non-linear equations
Two methods:
(i) Bracket/Close method :
(a) Bisection method
(b) False Position method
(ii) Open method :
(a) Fixed point iteration method
(b) Newton-Raphson method

3. Bracket/Close method
(a)Bisection method
The bisection method in
mathematics is a root finding
method which repeatedly
bisects an interval and then
selects a subinterval in which a
root must lie for further
processing. It is also known asprocessing. It is also known as
mid-point method.
Theorem: An equation f(x)=0,
where f(x) is a real continuous
function, has at least on root
between a and b if f(a)*f(b)<0.

4. Algorithm of Bisection method
Bisection method Steps (Rule)
Step-1: Find points a and b such that a<b and f(a)⋅f(b)<0.
Step-2: Take the interval [a,b] and find mid value c=(a+b)/2Step-2: Take the interval [a,b] and find mid value c=(a+b)/2
Step-3: If f(c)=0 then c is an exact root and stop
the algorithm.
else if f(a)⋅f(c)<0 then the root lies between a and c, so update b=c and a=a.
else if f(a)⋅f(c)>0 then the root lies between c and b, so update a=c and b=b.
Step-4: Repeat steps 2 & 3 until f(xi)=0 or |f(xi)|≤Accuracy.

5. The absolute relative approximate error:
Error = |[(new value of c – old value of c)/ new value of c]| *100%
Problem: Find the root of f(x)=x^2-3 using bisection method
with interval [1,2].

6. Advantages and Disadvantages of
Bisection method
Advantages:
• The bisection method is always convergent. Since the method brackets the
root, so the method is guaranteed to converge.
• Error can be controlled. As the iterations are conducted, the interval gets
halved, so one can guarantee the error in the solution of the equation.
• It is also considered to be the safest and simplest method.
Disadvantages:
• The convergence of the bisection method is slow as it is simply based on
halving the interval.
• If one of the initial guesses is closer to the root, it will take larger number
of iterations to reach the root.
• If f(x) is such that it just touches the x-axis, it will be unable to find the
lower and upper guess.

7. (b)False Position method
The poor convergence of the bisection
method motivate the use of better
techniques. One such method is
the Method of False Position.
Here, we start with an initial interval [a,
b], and we assume that the function
changes sign only once in this interval.changes sign only once in this interval.
Now we find 'c' in this interval, which is
given by the intersection of the x axis
and the straight line passing
through (a, f(a)) and (b, f(b)).
C =

8. Algorithm for False Position method
False Position method Steps (Rule)
Step-1:Find points a and b such that a<b and f(a)⋅f(b)<0.
Step-2: Take the interval [a, b] and find next valueStep-2: Take the interval [a, b] and find next value
c=[{a f(a)-b f(b)}/{f(b)-f(a)}]
Step-3: If f(c)=0 then c is an exact root, else if f(a)⋅f(c)<0 then update
b=c and a=a, else if f(a)⋅f(c)>0 then update a=c and b=b.
Step-4: Repeat steps 2 & 3 until f(xi)=0 or |f(xi)|≤Accuracy.

9. The absolute relative approximate error
Error=|[(new value of c – old value of c)/ new value of c]|*100%
Problem: Find the root of f(x)=x^2-3 using False Position
method with interval [1,2].

10. Open method
(a) Fixed point iteration method
• Rearrange the function f(x)=0 to x=g(x), so that x is on the left side
of the equation:
• Now if is the initial guess of the root, a new estimate can
)(
)(0)(
1 ii xgx
xxgxf



1x 1ix• Now if is the initial guess of the root, a new estimate can
be expressed by the iterative formula.
• Approximate error,
1x 1ix
)(1 ii xgx 

11. Steps of Simple Fixed Pint Iteration
• 1. Rearrange the equation f(x) = 0 so that x is on the left hand side
and g(x) is on the right hand side.
– e.g f(x) = x2-2x-1 = 0  x= (x2-1)/2
g(x) = (x2-1)/2
• 2. Set xi at an initial guess xo.• 2. Set xi at an initial guess xo.
• 3. Evaluate g(xi)
• 4. Let xi+1 = g(xi), and set xi at xi+1.
• 5. Find a=(Xi+1 – xi)/Xi+1
• 6. Repeat steps 3 through 5 until |a|<= a

12. Example: Simple Fixed-Point Iteration
f(x) = e-x - x
1. f(x) is manipulated so that we get
x=g(x) g(x) = e-x
2. Thus, the formula predicting the new
value of x is: x = e-xivalue of x is: xi+1 = e-xi
3. Guess xo = 0
4. The iterations continues till the approx.
error reaches a certain limiting value

13. Example: Simple Fixed-Point Iteration
• i xi g(xi) ea% et%
• 0 0 1.0
• 1 1.0 0.367879 100 76.3
• 2 0.367879 0.692201 171.8 35.1
• 3 0.692201 0.500473 46.9 22.1• 3 0.692201 0.500473 46.9 22.1
• 4 0.500473 0.606244 38.3 11.8
• 5 0.606244 0.545396 17.4 6.89
• 6 0.545396 0.579612 11.2 3.83
• 7 0.579612 0.560115 5.90 2.2
• 8 0.560115 0.571143 3.48 1.24
• 9 0.571143 0.564879 1.93 0.705
• 10 0.564879 1.11 0.399

14. (b) Newton - Raphson method
Newton - Raphson method is a
widely-used classical method for
finding the solution to a
nonlinear univariate function
of f(x) on the interval [a,b]. It is
also referred to as the Newton-also referred to as the Newton-
Raphson method.

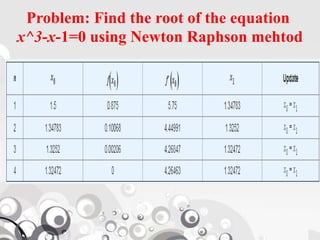
15. Algorithm for Newton Raphson method
Newton Raphson method Steps (Rule)
Step-1:Find points a and b such that a<b and f(a)⋅f(b)<0.
Step-2:Take the interval [a,b] and find next value x0=(a+b)/2Step-2:Take the interval [a,b] and find next value x0=(a+b)/2
Step-3:Find f(x0) and f′(x0)
x1=x0-(f(x0)/f′(x0))
Step-4:If f(x1)=0 then x1 is an exact root, else x0=x1
Step-5:Repeat steps 2 to 4 until f(xi)=0 or |f(xi)|≤Accuracy

16. Problem: Find the root of the equation
x^3-x-1=0 using Newton Raphson mehtod