Transformasi Laplace merupakan transformasi integral yang digunakan untuk merubah persoalan diferensial berkala menjadi persoalan aljabar. Transformasi Laplace memiliki sifat linearitas dan keberadaannya tergantung pada kontinuitas dan keterbatasan eksponensial fungsi.

1. 6. TRANSFORMASI
LAPLACE
1KPB-6-firda

2. Definisi Transformasi Laplace
Misal fungsi f(t) terdefinisi untuk t >0, maka
Transformasi Laplace dari f(t) didefinisikan
sebagai:
0 0
[ ( )] ( ) lim ( )
b
st s t
b
L f t e f t dt e f t dt
∞
− −
→∞
= =∫ ∫
Agar diperoleh TL dari fungsi f(t) maka Integral Tak
Wajar harus konvergen (Nilai limit ada dan berhingga).
I / 2KPB-6-firda

3. • Transformasi Laplace (TL) merupakan klas dari
Transformasi Integral
• Penggunaan Transformasi Laplace :
– Merubah bentuk PDB menjadi persamaan aljabar
Notasi: L[f(t)]=F(s)
I / 3KPB-6-firda

4. Akan ditentukan Transformasi Laplace dari fungsi
berikut :
1. f(t) = 1
2. f(t) = t
3. f(t) = t2
4. f(t) = t3
5. f(t) = tn
4KPB-6-firda

5. 1. Transformasi Laplace dari fungsi f(t) = 1
1
lim
0
s t
b
b
e
s
−
→∞
 −
=  
 
0 0
[1] .1 lim
b
st st
b
L e dt e dt
∞
− −
→ ∞
= =∫ ∫
( )1
lim 1sb
b
e
s
−
→∞
= −
−
( )
1 1
0 1
s s
= − =
−
[ ]
1
( ) 1 ( ) [1] 0f t F s L s
s
= ⇔ = = >
Bila s > 0 maka limit akan ada dan berhingga
I / 5KPB-6-firda

6. 2. TL dari Fungsi (t) = t
0 0
[ ] lim
b
st st
b
L t e t dt e t dt
∞
− −
→∞
= =∫ ∫
0
1 1
lim
0
b
st st
b
b
t e e dt
s s
− −
→∞
 
= + 
−  
∫
0
1 1
lim . lim
b
st
sbb b
b
e dt
s se
−
→∞ →∞
= +
− ∫
[ ]2
1
( ) ( ) [ ] 0f t t F s L t s
s
= ⇔ = = >
1
s
I / 6KPB-6-firda

7. 3. TL dari Fungsi f(t) = t2
2 2 2
0 0
[ ] lim
b
st st
b
L t e t dt e t dt
∞
− −
→∞
= =∫ ∫
2
0
1 2
lim
0
b
st st
b
b
t e e t dt
s s
− −
→∞
 
= + 
−  
∫
2
0
1 2
lim lim
b
st
sbb b
b
e t dt
s se
−
→∞ →∞
= +
− ∫
[ ]2 2
3
2
( ) ( ) [ ] 0f t t F s L t s
s
= ⇔ = = >
2
1
s
I / 7

8. 4. Transformasi Laplace dari Fungsi
[ ]
1
( ) 1 ( ) [1] 0f t F s L s
s
= ⇔ = = >
[ ]2
1
( ) ( ) [ ] 0f t t F s L t s
s
= ⇔ = = >
[ ]2 2
3
2
( ) ( ) [ ] 0f t t F s L t s
s
= ⇔ = = >
[ ]3 3
4
6
( ) ( ) [ ] 0f t t F s L t s
s
= ⇔ = = >
[ ]1
!
( ) ( ) [ ] 0n n
n
n
f t t F s L t s
s +
= ⇔ = = >
2 1
2.1
( )F s
s +
=
3 1
3.2.1
( )F s
s +
=
( ) n
f t t=
I / 8
KPB-6-firda

9. 5. TL dari Fungsi ( ) at
f t e=
0
[ ]at st at
L e e e dt
∞
−
= ∫
( )
0
lim
b
s a t
b
e dt
− −
→∞
= ∫
( )1
lim
0
s a t
b
b
e
s a
− −
→∞
 
= − ÷
− 
( ) 01
lim s a b
b
e e
s a
− −
→∞
   = − − ÷  − 
( )
1 1
lim 1s a bbs a e −→∞
  
= − − ÷  −   
Bila s – a > 0
maka limit
ada dan
berhingga
I / 9KPB-6-firda

10. 1
[ ] .at
L e
s a
=
−
1
( ) ( ) [ ]at at
f t e F s L e
s a
= ⇔ = =
−
I / 10KPB-6-firda

11. ( ) sinf t at=
0 0
[sin ] sin lim sin
b
st st
b
L at e at dt at e dt
∞
− −
→∞
= =∫ ∫
6. TL dari fungsi
0
1 1
limsin lim cos
0
b
st st
b b
b
at e e a at dt
s s
− −
→∞ →∞
 
= − + ÷
 
∫
0
lim cos .
b
st
b
a
at e dt
s
−
→∞
= ∫
0
1
lim cos lim sin .
0
b
st st
b b
ba a
at e at e dt
s s s
− −
→∞ →∞
   
= − −  ÷ 
   
∫
2
2 2
0
lim sin .
b
st
b
a a
at e dt
s s
−
→∞
= − ∫
bentuk
udv∫
I / 11KPB-6-firda

12. 2
2 2
0
sin . sta a
at e dt
s s
∞
−
= − ∫
0
[sin ] sin st
L at at e dt
∞
−
= ∫
2
2 2
0 0
sin . sin .st sta a
at e dt at e dt
s s
∞ ∞
− −
+ =∫ ∫
2
2 2
0
1 sin . sta a
at e dt
s s
∞
− 
+ = ÷
 
∫
2
2 2 2 2 2
0
sin . .st a s a
at e dt
s s a s a
∞
−
= =
+ +∫
2 2
( ) sin ( ) [sin ]
a
f t at F s L at
s a
= ⇔ = =
+
I / 12
KPB-6-firda

13. Tabel Transformasi Laplace
1
!
n
n
s +
1
s a−
2 2
a
s a+
2 2
s
s a+
2 2
a
s a−
2 2
s
s a−
at
e
n
t
sin at
cos at
sinh at
cosh at
s a>
0s >
( )f t [ ( )] ( )L f t F s=
1
1
s
13

14. Sifat Transformasi Laplace
• Keberadaan :Transformasi Laplace dari f(t) dengan t ≥
0 ada bila f(t) kontinu bagian demi bagian dan terbatas
eksponensial untuk t ≥ 0
• Ketunggalan : Transformasi Laplace dari suatu fungsi
adalah tunggal yaitu bila F1(s) dan F2(s) merupakan
transformasi Laplace dari f(t) maka F1(s) = F2(s)
I / 14KPB-6-firda

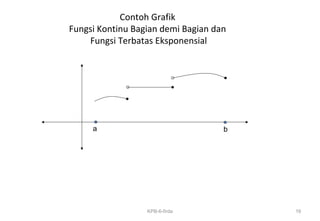
15. Fungsi Kontinu Bagian demi Bagian dan
Fungsi Terbatas Eksponensial
Fungsi f(t) disebut kontinu bagian demi bagian pada
interval [ a,b ] bila
1. Interval [ a,b ] dapat dibagi menjadi sub-sub interval
yang berhingga banyaknya yang menyebabkan f(t)
kontinu pada sub-sub interval tersebut
2. Limit dari f(t) pada setiap ujung sub interval bernilai
hingga
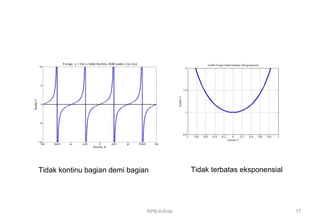
Fungsi f(t) disebut terbatas eksponensial pada interval
[a,b ] bila terdapat bilangan real M dan r sehingga
berlaku| ( ) | [ , ]rt
f t Me t a b≤ ∀ ∈
2
x
y e=Fungsi tidak terbatas eksponensial
15KPB-6-firda

16. Contoh Grafik
Fungsi Kontinu Bagian demi Bagian dan
Fungsi Terbatas Eksponensial
a b
16KPB-6-firda

17. Tidak kontinu bagian demi bagian Tidak terbatas eksponensial
17KPB-6-firda

18. ( ) ( )( ) ( ) ( )L a f t b g t a F s bG s+ = +
Sifat Linear Transformasi Laplace:
Bukti:
( ) ( )( )
0
( ( ) ( ))st
L a f t b g t e af t bg t dt
∞
−
+ = +∫
0 0
. ( ) . ( )st st
e af t dt e bg t dt
∞ ∞
− −
= +∫ ∫
0 0
. ( ) . ( )st st
a e f t dt b e g t dt
∞ ∞
− −
= +∫ ∫
( ) ( )a F s bG s= + terbukti
18KPB-6-firda

19. 5
( ) 3 t
f t e−
=
1 3
( ) 3. .
5 5
F s
s s
= =
+ +
Contoh :
1. Tentukan TL dari
Jawab :
5
( ) 3 t
F s L e−
 =  
5
3. t
L e−
 =  
I / 19KPB-6-firda

20. ( )
2
( ) 2f t t= +
( )
2 2
( ) 2 4 4f t t t t= + = + +
2
3 2 3
2 4 42 4 4
( ) .
s s
F s
ss s s
+ +
= + + =
2. Tentukan TL dari
Jawab :
2
( ) ( 4 4)F s L t t= + +
2
( ) 4 ( ) 4 (1)L t L t L= + +
I / 20KPB-6-firda

21. 4 3
cos5t
L e t t + − = 3.
4 2
1 6
4 25
s
s s s
= + −
− +
4
4. 3sinh 4 4L t t − = 
2 5
12 48
16s s
= −
−
4 2
1 3!
4 25
s
s s s
+ −
− +
2 5
4 4!
3. 4.
16s s
−
−
I / 21KPB-6-firda

22. 1 1 at
L e
s a
−  
= ÷
− 
( )1
( ) ( )f t L F s−
=
Invers Transformasi Laplace
( ) ( ) ( )1 1 1
( ) ( ) ( ) ( )L c F s dG s cL F s dL G s− − −
+ = +
I / 22KPB-6-firda

23. ( )
4s3s
1
sF 2
−−
=
( )
( ) ( )2
1 1
3 4 4 1
F s
s s s s
= =
− − − +
1 1
5 5
( )
4 1
F s
s s
−
= +
− +
4
1 1/ 5 1/ 5
( ) .
4 1 5 5
t t
e e
f t L
s s
−
−  
= − = − − + 
4 1
A B
s s
= +
− +
1 1 at
L e
s a
−  
= ÷
− 
2. Tentukan f(t) dari
Jawab :
Maka
diperoleh A=1/5, B=-1/5.
Contoh:
1 41
1.
4
t
L e
s
− − 
= ÷
+ 
I / 23KPB-6-firda

24. Soal Latihan
1. Tentukan Transformasi Laplace dari fungsi
a) f(t) = sinh at
b) f(t) = cosh at
2. Tentukan invers dari
2
. ( )
3 2
s
a F s
s s
=
+ +
2
. ( )
9
s
b F s
s
=
−
2
3 12
. ( )
( 8)( 1)
s
c F s
s s
−
=
+ −
2
2
4 2 1
. ( )
( 2)( 3)
s s
d F s
s s
+ −
=
+ −
2
1 2 1
. ( )
2 5 36
s
e F s
s s
−
= +
+ +
I / 24KPB-6-firda

25. Misal fungsi f(t) mempunyai transformasi Laplace,
F(s) = L ( f(t) ), maka transformasi Laplace dari fungsi
g(t) = eat
f(t) adalah
( ) ( )
0
( ) ( )at st at
L e f t e e f t dt
∞
−
= ∫
( )
0
( )
s a t
e f t dt
∞
− −
= ∫ ( )F s a= −
Invers Transformasi Laplace :
( )( ) )t(feasFL
at1
=−
−
Pergeseran terhadap sumbu s
25KPB-6-firda

26. ( ) sin 3f t t=
2
( ) ( )t
g t e f t=
2
3
( )
9
F s
s
=
+
Tentukan TL dari
2
( ) sin 3t
g t e t=


( )
2
3
( ) ( 2)
2 9
G s F s
s
= − =
− +
( ) ( )( )at
L e f t F s a= −
Contoh:
Jawab :
26KPB-6-firda

27. ( )
2
1 1
s
s
=
+ + ( ) ( )
2 2
1 1
1 1 1 1
s
s s
+
= −
+ + + +
1 2
( )
1
s
F s
s
=
+
2 2
1
( )
1
F s
s
−
=
+
2
( )
2 2
s
G s
s s
=
+ +
Contoh
Tentukan Invers dari :
Jawab :
2
( )
2 2
s
G s
s s
=
+ +
1( ) cosf t t→ =
2 ( ) sinf t t→ = −
Maka
1 2( ) ( 1) ( 1) ( ) (cos sin ).t
G s F s F s g t e t t−
= + + + → = −
1 1 2 2( ) ( 1), ( ) ( 1)G s F s G s F s= + = +
1( )G s
2 ( )G s
27KPB-6-firda

28. Soal Latihan
1. Tentukan Transformasi Laplace dari fungsi :
a)
b)
2. Cari f(t) untuk F(s) berikut :
a)
b)
2 2
( ) t
f t t e−
=
( ) t
f t e Cos t−
=
2
2
4 5
s
s s
−
− +
( )
2
2 1
1 4
s
s
+
+ +
28KPB-6-firda

29. • Misal fungsi f(t) dan turunannya kontinu dan terbatas
eksponensial, maka f(t) dan f ’(t) mempunyai transformasi
Laplace
• Transformasi Laplace dari turunan orde n fungsi f(t) ditentukan
sebagai berikut :
0
lim ( ) ( )
0
st st
a
a
e f t s e f t dt
∞
− −
→∞
= + ∫
[ '( )] ( ( )) (0)L f t sL f t f= −
TL dari turunan fungsi tingkat-n
( )( ) ( )
0
' 'st
L f t e f t dt
∞
−
= ∫
0
lim ( ) (0) ( )sa st
a
e f a f s e f t dt
∞
− −
→∞
= − + ∫
(0) ( ( ))f sL f t= − +
[ '( )] ( ) (0)L f t sF s f= −atau
I / 29KPB-6-firda

30. ( )( ) ( )
0
'' ''st
L f t e f t dt
∞
−
= ∫
2
( ( )) (0) '(0)s L f t sf f= − −
0
lim '( ) '( )
0
st st
a
a
e f t s e f t dt
∞
− −
→∞
= + ∫
0
lim '( ) '(0) '( )sa st
a
e f a f s e f t dt
∞
− −
→∞
= − + ∫
'(0) ( '( ))f sL f t= − +
'(0) ( ( ( )) (0))f s sL f t f= − + −
2
( ''( )) ( ) (0) '(0)L f t s F s sf f= − −
Maka
I / 30KPB-6-firda

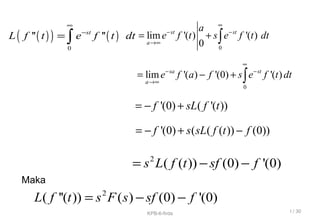
31. ( )( ) 3 2
"' ( ) (0) '(0) ''(0)L f t s F s s f sf f= − − −
( )
( )( ) ( )11 2
( ) (0) '(0) ... (0)n nn n n
L f t s F s s f s f f −− −
= − − − −
Sehingga kita peroleh:
[ '( )] ( ) (0)L f t sF s f= −
2
( ''( )) ( ) (0) '(0)L f t s F s sf f= − −
I / 31KPB-6-firda

32. Tentukan dulu turunan fungsi sampai tingkat ke –2 , dan evaluasi di 0;
 f(t) = sin at  f( 0 ) = 0
 f ‘ (t) = a cos at  f ‘ ( 0 ) = a
 f “ (t) = - a2
sin at
Contoh : Tentukan TL dari f(t) = sin at
( )( ) 2
" ( ( )) (0) '(0)L f t s L f t sf f= − −
( ) ( )2 2
sin sin (0) '(0)L a at s L at sf f− = − −
( ) 2 2
sin
a
L at
s a
=
+
Invers Transformasi : 1
2 2
1 sin at
L
s a a
−  
= ÷
+ 
( )2 2
sin (sin )s L at a L at a+ =
I / 32
( ) 2 2
sin ( )L at s a a+ =
KPB-6-firda

33. Tentukan TL dari fungsi berikut :
1. f(t) = sin 2t
2. f(t) = cos at
3. f(t) = sin ( t – ½ π)
4. f(t) = cos ( t + π )
5. f(t) = sin2
t
6. f(t) = cos2
t
Soal Latihan
I / 33KPB-6-firda

34. • Bentuk persamaan diferensial koefisien konstan dengan
nilai awal dinamakan masalah nilai awal.
• Contoh :
• Dengan mengasumsikan y(t) = f(t) maka didapatkan :
Masalah Nilai Awal
" ' ( )
(0) , '(0)
a y b y c y r t
y k y m
+ + =
= =
( ) ( )' (0)L y sL y y= −
( ) ( )2
" (0) '(0)L y s L y sy y= − −
I / 34KPB-6-firda

35. Contoh : Tentukan Solusi Masalah Nilai Awal
" 3 ' 2 ; (0) 1, '(0) 0y y y t y y+ + = = − =
( )" 3 ' 2 ( )L y y y L t+ + =
( ) ( )2
2
1
3 2 ( ) 3 ,s s L y s
s
+ + = − + ( )
( ) ( )
3 2
2
3 1
2 1
s s
L y
s s s
− − +
→ =
+ +
( )
( )2
3 1 3 1
4 2 4 2 1
L y
s s s s
−
= + + −
+ +
( ) 23 3
4 2 4
t tt
y t e e− −−
= + + −
Jawab ;
selesaikan dengan pecahan parsial, diperoleh
Maka
I / 35KPB-6-firda

36. Soal Latihan
Tentukan solusi dari masalah nilai awal berikut dengan Laplace:
1. y ”+ 2 y ’- 8y = 0, y(0) = 0, y ‘(0) = 6
2. y “ + 4y = 1 – 2 t, y(0) = y ‘(0) = 0
3. y “ – 2 y ‘ – 3y = 1, y(0) = 1 , y ‘(0) = 0
4. y “ + 4y = 0, y(0) = -1 , y ‘(0) = 0
5. y “ - 4y = e2t
, y(0)= 0, y ‘(0) =1
6. y “ – 4 y ‘ = sin t, y(0) = y ‘ (0) = 0
36KPB-6-firda