Transformasi Laplace digunakan untuk mengubah persamaan diferensial dalam domain waktu menjadi persamaan aljabar dalam domain s, memungkinkan memanipulasi persamaan dengan mudah untuk menghasilkan solusi. Invers transformasi Laplace diperlukan untuk mengembalikan solusi ke domain waktu asli.

1. TRANSFORMASI
LAPLACE

2. TRANSFORMASI LAPLACE
• Transformasi adalah teknik atau formula matematis
yang digunakan untuK mengubah representasi
persamaan matematika dari satu bentuk ke bentuk
representasi yang lain. Adanya transformasi
mengharuskan juga adanya inverse transformasi, yang
melakukan hal yang sebaliknya
• Transformasi diperlukan sebagai alat bantu untuk
memecahkan persoalan matematika yang rumit

3. • Transformasi Laplace merupakan salah satu tools yang
digunakan untuk menyelesaikan persamaan differensial.
• Transformasi Laplace mengkonversikan persamaan differensial
(dalam domain t) kedalam persamaan aljabar dalam domain s.
• Memungkinkan memanipulasi persamaan aljabar dengan
aturan sederhana untuk menghasilkan solusi dalam domain s.
• Solusi dalam domain t dapat diperoleh dengan melakukan
operasi inverse transformasi Laplace

4. •Terdapat beberapa tipe/jenis transformasi yang
digunakan, tergantung pada persamaan matematika
yang ingin dicari penyelesaiannya. Beberapa contoh
transformasi yang digunakan dalam bidang teknik
antara lain :
1. Transformasi Laplace
2. Transformasi Fourier
3. Trasnformasi Z
4. Trasnformasi Wavelet
5. Dll

5. Contoh penggunaan Transformasi
• Dalam penggunaan logaritma dan inverse-nya, yaitu fungsi perpangkatan.
Misalnya, Apabila diinginkanbuntuk menghitung hasil dari : 1234 x 5678
tanpa menggunakan kalkulator, namun dengan menggunakan tabel logaritma,
maka solusi hasil perhitungan 1234 x 5678 dapat dicari dengan mudah.

6. Persamaan diferensial dan
Trasformasi Laplace
• Persamaan Differensial yang diperoleh dari pemodelan matematik suatu
sistem mewakili proses dinamik dari sistem tersebut dimana responsenya
akan bergantung pada masukannya
• Solusi dari persamaan differensial terdiri dari solusi steady state (didapat
jika semua kondisi awal nol) dan solusi transien (mewakili pengaruh dari
kondisi awal).
• Transformasi Laplace mengkonversikan persamaan differensial (dalam
domain t) kedalam persamaan aljabar dalam domain s.
• Memungkinkan memanipulasi persamaan aljabar dengan aturan
sederhana untuk menghasilkan solusi dalam domain s.
• Solusi dalam domain t dapat diperoleh dengan melakukan operasi inverse
transformasi Laplace 6

7. Definisi
)
(t
F
suatu fungsi t dan t > 0, maka transformasi Laplace dari F(t) dinotasikan dengan
L{F(t)} yang didefinisikan oleh





`
0
)
(
)
(
)}
(
{ s
f
dt
t
F
e
t
F
L st
)}
(
{ t
F
L

Transformasi Laplace digunakan untuk mengubah fungsi y(t) yang berada dalam kawasan waktu
ke kawasan s. Solusi dari persamaan diferensial didapat dengan mengubah persamaan diferensial
(yang merupakan fungsi waktu) dari kawasan waktu ke kawasan s dengan menggunakan
transformasi laplace, sebagaimana ditunjukkan pada gambar di bawah.

11. Contoh:
1. Bila fungsi f(t) = A maka kita misa menentukan nilai L[f(t)]
dt
e
A
A
L
t
f
L t
s
.
]
[
)]
(
[
0








 0
]
[ st
e
s
A
s
A
s
A
e
e
s
A






 
)
1
0
(
]
1
1
[ 0
Sebagai pemahaman bagi pembaca, berikut ini diberikan beberapa
contoh transformasi Laplace suatu fungsi,Tentukan transformasi
Laplace fungsi berikut

12. 2. f(t) = At
Dibantu dengan formula integral partsial yaitu
dt
e
At
At
L st




0
.
]
[
dt
e
t
A st




0
.
 

 V
U
UV
UV '
'









0
0
.
.
]
[ st
st
de
t
s
A
dt
e
t
A
At
L

13.  

2
0
0
0
)
1
0
(
1
0
]
[
1
)
1
0
0
(
.
1
]
.
[
s
A
s
s
A
e
s
s
A
dt
e
e
t
s
A
st
st
st




































0
0
.
.
]
[ st
st
de
t
s
A
dt
e
t
A
At
L

14. 3. f(t) = e-at











0
)
(
0
.
]
[
dt
e
dt
e
e
e
L
t
s
a
st
at
at


s
a
s
a
e
s
a
t
s
a












1
)
1
0
(
)
(
1
)
(
1
0
)
(

15. )
(t
F





`
0
)
(
)
(
)}
(
{ s
f
dt
t
F
e
t
F
L st
)}
(
{ t
F
L






`
0
)
(
)
(
)}
(
{ s
f
dt
t
F
e
t
F
L st





p
st
p
dt
t
F
e
Lim
0
)
(
Karena nilai integral di atas tidak wajar dikarenakan batas atas bernilai
tak hingga ∞ ,
Maka kita bisa menyelesaikan transformasi ini dapat juga diselesaiakn dengan
menggunakan konsep limit

16. Contoh dengan menggunakan Metoda limit

17. Contoh 2

18. Contoh 3

19. Sifat-sifat Transformasi Laplace
• Sifat Linier.
Jika c1 dan c2 konstan, sedang F1(t) dan F2(t) fungsi-fungsi yang
transformasi laplacenya masing-masing f1(s) dan f2(s), maka:
   
   
   
 
   
s
f
c
s
f
c
t
F
L
c
t
F
L
c
t
F
c
t
F
c
L
2
2
1
1
2
2
1
1
2
2
1
1






20. •Sifat Translasi
Jika L[F(t)] = f(s) maka : L[eat F(t) ] = f(s-a)
• Sifat Pengubahan Skala
Jika L[F(t)] = f(s), maka :
L[F(at)] = 





a
s
f
a
1

21. • Sifat Integral
Jika L[F(t)] = f(s) maka
• Sifat Turunan
Jika L[F(t)] = f(s) maka
L{F’(t)} = sf(s) – F(0)
   
s
s
f
du
u
F
L
t








0
)
0
(
)
0
(
...
)
0
(
'
)
0
(
)
(
)]
(
[ )
1
(
)
2
(
2
1 








 n
n
n
n
n
n
F
sF
F
s
F
s
s
f
s
t
F
L

22. •Sifat Perkalian dengan tn
Jika L[F(t)] = f(s) maka
L[tn F(t)]= (-1) = (-1)n fn(s)
•Sifat Pembagian oleh t
Jika L[F(t)] = f(s) maka
𝑑𝑛
𝑑𝑠𝑛
𝑓(𝑠)









0
)
(
)
(
du
u
f
t
t
F
L

28. Teorema Transformasi Laplace
• Linieritas
 
   
   
     
s
F
s
F
t
f
t
f
L
s
aF
t
af
L
2
1
2
1 



     
       
dt
df
f
s
F
s
dt
t
f
d
L
f
s
sF
dt
t
df
L
0
0
0
2
2
2

















28
 
     
dt
s
f
s
s
F
dt
t
f
L

 

0
   
s
sF
t
f
s
t 


 lim
lim
0
   
s
sF
t
f
s
t 0
lim
lim




 
   
s
F
e
t
f
L s
 


• Differensiasi
• Integrasi
• Nilai awal
• Nilai akhir
• Pergeseran waktu

29. Tabel transformasi laplace
•Jenis transformasi integral ini memiliki sejumlah sifat yang
membuatnya amat berguna bagi analisis sistem dinamik
linier.
•Perubahan persamaan integral dan diferensial menjadi
bentuk polinomial menyederhanakan proses penyelesaian.
• Dari Urain penyelessian di atasdapt dibuatkan table sebagai
berikut
Mengingat Bentuk Intergral yang terkadang menjenuhkan maka
integral tersebut biasanya dibentuk table

30. Tabel Transformasi Laplace untuk fungsi sederhana
f(t) L(f) f(t) L(f)
1 1 1/s 7
cos at
2 t 1/s2 8
sin at
3 t2 2!/s3 9
cosh at
4 tn
(n=0, 1,…)
10
sinh at
5 ta
(a positive)
11
ebt cos at
6 eat 12
ebt sin at
1
!

n
s
n
1
)
1
(



a
s
a
a
s 
1
1
)
1
(



a
s
a
2
2
a
s
s

2
2
a
s
a

2
2
a
s
s

2
2
a
s
a

2
2
)
( a
b
s
b
s



2
2
)
( a
b
s
a



31. Contoh Tentukan

33. Sehingga bila kita kembalikan ke dalam inversnya akan berlaku

36. Invers transformasi laplace
•Jika mengubah sinyal analog kontinyu dari domain
waktu menjadi domain frekuensi menggunakan
transformasi laplace, maka untuk mengembalikan
sinyal tersebut dari domain frekuensi menjadi
domain waktu menggunakan invers transformasi
laplace.

37. Jika transformasi Laplace suatu fungsi F(t) adalah f(s), yaitu jika
maka F(t) disebut suatu transformasi Laplace Invers
dari f(s).
Secara simbolis ditulis dan L disebut operator
transformasi Laplace invers.
INVERS TRANSFORMASI LAPLACE
Invers Transformasi Laplace adalah proses kebalikan dari Transformasi
Laplace.
jika diberikan suatu transformasi Laplace, Maka kita harus mencari
fungsi t dari laplace tsb.

38. Sebagai contoh, kita ketahui adalah transformasi laplace
dari f(t) =Sin at maka kita dapat menuliskan:

39.    
 
s
F
L
t
f 1


   
   





0
dt
e
t
f
t
f
L
s
F st
39
Transformasi Laplace F(s)
dari fungsi f(t)
Inverse Transformasi Laplace
Fungsi f(t) haruslah real dan kontinyu sepanjang interval waktu
yang akan dievaluasi, jika tidak, maka transformasi Laplace tidak
dapat digunakan.

40. Sifat-sifat Invers Transformasi
Laplace
•Sifat Linier.
Jika c1 dan c2 konstan, sedang f1(s) dan f2(s) berturut-turut
transformasi laplace dari F1(t) dan F2(t), maka:
a). L-1 [ c1 f1 (s) ] = c1 L-1[ f1 (s) ] = c1 F1 (t)
L-1 [ c2 f2 (s) ] = c2 L-1[ f2 (s) ] = c1 F2 (t)
b). L-1 [ c1 f1 (s) + c2 f2 (s) ] = L-1 [ c1 f1 (s) ] + L-1 [ c2 f2 (s) ]
= c1 F1 (t) + c2 F2 (t)

41. Contoh

42. • Sifat Translasi
Jika L-1[f(s)] = F(t)
maka :
L-1[f(s-a) ] = eat F(t)
• Sifat Pengubahan Skala
Jika L-1[f(s)] = F(t), maka :
L-1[f(as)] = 





a
t
F
a
1

43. Contoh

44. • Sifat Integral
Jika L-1[f(s)] = F(t), maka
L-1
• Sifat Turunan
Jika L-1[f(s)] = F(t), maka
L-1[fn(s)] = = (-1)n tn F(t)
   
t
t
F
du
u
F
s








~
]
)
(
[
L1
-
s
f
ds
d
n
n

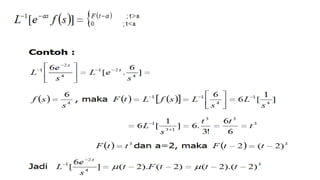
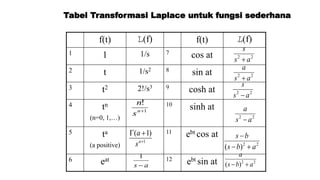
50. Invers Transformasi Laplace untuk fungsi sederhana
f(s) L-1[f(s)] f(s) L-1[f(s)]
1 1/s 1 7
cos at
2 1/s2 t 8
sin at
3 t2 2!/s3 9
cosh at
4
tn/n! 10
sinh at
5 ta/ (a+1) 11
ebt cos at
6 eat 12
ebt sin at
1
1

n
s
1
1

a
s
a
s 
1
2
2
a
s
s

2
2
1
a
s 
2
2
a
s
s

2
2
1
a
s 
2
2
)
( a
b
s
b
s



2
2
)
( a
b
s
a



a
1
a
1

51. Metode Pecahan Parsial untuk mencari invers
Transformasi Laplace
•Jika f(s) berbentuk pecahan parsial yang pembilang dan
penyebutnya berbentuk polinomial.
•Derajat P(s) < derajat Q(s), maka
)
(
)
(
)
(
s
Q
s
P
s
f 

52. •Jika akar-akar Q(s) berbeda, tidak ada yang sama,
•maka :
)
(
...
)
(
)
(
)
(
)
)...(
)(
(
)
(
)
(
2
2
1
1
2
1
n
n
n
p
s
A
p
s
A
p
s
A
s
f
p
s
p
s
p
s
s
P
s
f









t
n
p
n
t
p
t
p
e
A
e
A
e
A
t
F 





 ...
)
( 2
2
1
1

53. •Q(s) mempunyai akar rangkap
•maka F(t) sama dengan invers transformasi laplace dari
masing-masing suku.
)
(
...
)
(
)
(
...
)
(
)
(
)
(
)
)...(
(
)
(
)
(
)
(
2
2
1
1
2
1
12
1
11
2
1
n
n
r
r
n
r
p
s
A
p
s
A
p
s
A
p
s
A
p
s
A
s
f
p
s
p
s
p
s
s
P
s
f

















54. APLIKASI TRANSFORMASI LAPLACE
PADA PERSAMAAN DIFFERENSIAL ( PD )
Transformasi Laplace dapat digunakan untuk
menyelesaikan persamaan differensial biasa.
Metode ini akan menghasilkan solusi khusus
secara langsung yang sesuai dengan kondisi
awal yang diberikan.

56. Langkah–langkah untuk menyelesaikan PD
• Membentuk persamaan pembantu, yaitu gunakan transformasi
laplace pada kedua ruas dari PD yg diberikan dan gunakan kondisi
awal.
• Selesaikan persamaan aljabar (persamaan pembantu) itu dan
dapatkan Y = f(s) .
• Gunakan transformasi Laplace invers pada kedua ruas. Yang akan
memberikan solusi yang dibutuhkan, yaitu :
L-1 [Y] = L-1 [f(s)] atau y = F(t)

57. Contoh :
Selesaikan PD dibawah ini bila F(0) = 1, F’(0) = 1
Jawab :
PD diatas dapat ditulis dalam bentuk :
Y” – 2y’ + 2y = 0
•Gunakan transf. Laplace pada kedua ruasnya :
L{y”} – 2L{y’} + 2L{y} = L{0}
• L{y”} = s2f(s) – s F(0) – F’(0)
= s2f(s) – s.1 – 1 = s2f(s) – s – 1 ….(1)
0
2
2
2
2


 y
dt
dy
dt
y
d

58. • L{y’) = sf(s) - F(0) = sf(s) – 1 ……………………………..…………………(2)
• L{Y} = f(s) ………………………………………………………………………(3)
• Subtitusikan pers. (1) , (2) dan (3) kedalam transformasi laplace dari
PD yg diberikan, yaitu :
[s2f(s) – s – 1] – 2 [ s f(s) – 1 ] + 2f(s) = 0
(s2 -2s + 2)f(s) – s + 1 = 0
(s2 -2s + 2)f(s) = s - 1 →
2
2
1
)
( 2




s
s
s
s
f
1
)
1
(
1
)
( 2




s
s
s
f

59. • Gunakan Invers Transformasi Laplace pada kedua ruasnya, yaitu :
F(t) = et cos t
• Jadi solusi khusus PD yang memenuhi kedua kondisi awal diatas
adalah : F(t) = et cos t
]
1
)
1
(
1
[
)]
(
[ 2
1
1



 

s
s
L
s
f
L

66. Transformasi Laplace Untuk Solusi
Persamaan Differensial
Misalkan Diberikan persamaan differensial sbb:
       
t
f
t
y
dt
t
dy
dt
t
y
d
5
2
3
2
2



Dimana f(t) adalah fungsi unit step dengan kondisi awal
y(0)=-1 dan y´(0)=2.

67. Contoh:
Solusi Persamaan Differensial
     
s
s
Y
y
s
sY
y
sy
s
Y
s
1
5
)
(
2
)
0
(
3
3
)
0
´(
0
2






67
Transformasi Laplace menghasilkan:
Menggunakan teorema
differensiasi
transformasi Laplace
       
t
f
t
y
dt
t
dy
dt
t
y
d
5
2
3
2
2




68.    
)
2
3
(
5
)
(
5
)
(
)
2
3
(
5
)
(
2
3
3
2
2
2
2
2
2


















s
s
s
s
s
s
Y
s
s
s
Y
s
s
s
s
s
Y
s
sY
s
s
Y
s
Fungsi unit step dari
tabel transformasi
Laplace
Solusi dalam domain t
diperoleh dengan
invers transformasi
Laplace
       
t
f
t
y
dt
t
dy
dt
t
y
d
5
2
3
2
2




69. Selanjutnya
)
2
)(
1
(
5
)
2
3
(
5
)
(
2
2
2












s
s
s
s
s
s
s
s
s
s
s
Y
)
2
)(
1
(
5
)
2
(
)
1
(
)
(
2











s
s
s
s
s
s
C
s
B
s
A
s
Y
69
Invers transformasi Laplace dilakukan dengan memanipulasi penyebut
(denumerator) dalam fungsi Y(s) kedalam akar-akarnya:
Ekpansi dalam pecahan parsial,

70. 2
3
)
1
(
5
)]
(
)
2
[(
5
)
2
(
5
)]
(
)
1
[(
2
5
)
2
)(
1
(
5
)]
(
[
2
2
2
1
2
0






























s
s
s
s
s
Y
s
C
s
s
s
s
s
Y
s
B
s
s
s
s
s
sY
A
s
s
s
Dimana A, B dan C adalah koefisien

71. )
2
(
2
3
)
1
(
5
2
5
)
(





s
s
s
s
Y
t
t
e
e
t
y 2
2
3
5
2
5
)
( 




71
Persamaan Y(s) dalam bentuk pecahan parsial menjadi
Dengan invers transformasi Laplace (di dapat dari tabel),
persamaan dalam domain waktu y(t) menjadi
Dengan t ≥ 0

72. Prosedur Solusi pers. Differensial dengan:
Transformasi Laplace
1. Transformasi persamaan differensial ke dalam domain s
dengan transformasi Laplace menggunakan tabel
transformasi Laplace.
2. Manipulasi persamaan aljabar yang telah ditransformasikan
untuk mendapatkan variabel outputnya.
3. Lakukan ekspansi pecahan parsial terhadap persamaan
aljabar pada langkah 2.
4. Lakukan invers transformasi Laplace dengan tabel
transformasi Laplace untuk mendapatkan solusi dalam
domain t.
72

73. Ekspansi Pecahan Parsial:
• Transformasi Laplace dari suatu persamaan differensial f(t) lazimnya
diberikan dalam bentuk:
)
(
)
(
)
(
s
D
s
N
s
F 
)
)...(
)(
(
)
(
)
(
2
1 N
s
s
s
s
s
s
s
N
s
F




73
• Bentuk ekspansi pecahan parsial dari F(s) bergantung pada akar-akar persamaan
karakteristiknya (denumerator).
– Kasus 1: Persamaan karakteristik hanya memiliki akar real dan tidak sama
N(s) adalah numerator (pembilang) dalam s,
D(s) denumerator (penyebut) dalam s

74. )
(
...
)
(
)
(
)
(
2
2
1
1
N
N
s
s
K
s
s
K
s
s
K
s
F






 Ki (i=1,…,N) adalah konstanta
yang harus dicari
Dalam kasus tersebut pecahan parsialnya dapat dituliskan
dalam bentuk:

75. Ekspansi Pecahan Parsial:
)
)...(
)(
)...(
)(
(
)
(
)]
(
)
[(
1
1
2
1 N
i
i
i
i
i
i
i
i
s
s
i
i
s
s
s
s
s
s
s
s
s
s
s
N
s
F
s
s
K i


















M
n
n
n
n
n
n s
s
s
s
s
s
s
N
s
F
)
2
...(
)
2
(
)
2
(
)
(
)
( 2
2
2
2
2
1
2
2





 






75
• Kasus 2: Persamaan karakteristik hanya memiliki akar kompleks
Dalam kasus tersebut pecahan parsialnya dapat dituliskan dalam
bentuk:
Konstanta K dicari dengan persamaan berikut:
Jika persamaan karakteristik hanya memiliki M pasangan complex-conjugate, F(s) dapat
dituliskan sbb:

76. M
n
n
n
n
n
n
N s
s
s
s
s
s
s
s
s
s
s
s
s
N
s
F
)
2
...(
)
2
(
)
2
)(
)...(
)(
(
)
(
)
( 2
2
2
2
2
1
2
2
2
1 




 









76
• Kasus 3: Persamaan karakteristik memiliki akar real, tidak sama dan
kompleks
Dalam kasus tersebut pecahan parsialnya dapat dituliskan dalam bentuk:
M
n
n
M
M
n
n
n
n
N
N
s
s
B
s
A
s
s
B
s
A
s
s
B
s
A
s
s
K
s
s
K
s
s
K
s
F
)
2
(
...
)
2
(
)
2
(
)
(
...
)
(
)
(
)
(
2
2
2
2
2
2
2
1
2
2
1
1
2
2
1
1





 



















M
n
n
M
M
n
n
n
n s
s
B
s
A
s
s
B
s
A
s
s
B
s
A
s
F
)
2
(
...
)
2
(
)
2
(
)
( 2
2
2
2
2
2
2
1
2
2
1
1





 












Dimana Ai dan Bi konstanta yang dicari dengan menyamakan pangkat dalam s