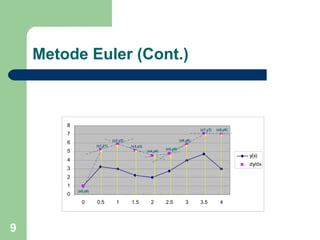
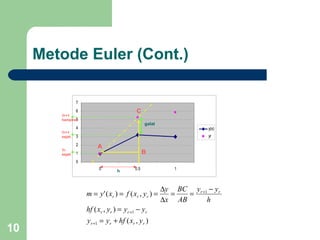
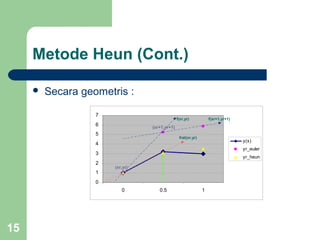
Dokumen tersebut membahas tentang persamaan diferensial biasa dan metode numerik untuk menyelesaikannya, yaitu metode Euler, Heun, dan Runge Kutta hingga orde 4. Metode-metode tersebut digunakan untuk memperoleh aproksimasi solusi persamaan diferensial dengan menghitung nilai fungsi pada setiap langkah iterasi.

1. 1
8. Persamaan Differensial Biasa
(PDB)
Euler, Heun, Runge Kutta 1-4

2. 2
Pendahuluan
 Persamaan Differensial :
gabungan dari fungsi yang tidak diketahui dengan turunannya.
 Kategori Persamaan Differensial :
– PD Biasa :
Persamaan Differensial yang hanya memiliki satu variabel bebas.
Berdasarkan turunan tertinggi yang dimiliki, PDB dikategorikan
menjadi :
 PDB Orde 1 : turunan tertingginya adalah turunan pertama
 PDB Orde 2 : turunan kedua merupakan turunan tertinggi
 PDB Orde 3 : turunan ketiga merupakan turunan tertingginya.
 Dan seterusnya
– PD Parsial
Persamaan Differensial yang memiliki lebih dari satu variabel
bebas.

3. 3
Pendahuluan Cont.
Contoh Persamaan :
yx
dx
dy +=
Turunan dilambangkan dengan : dy/dx atau f’(x) atau y’, sedangkan fungsi yang tidak diketahui
dilambangkan dengan keberadaan variabel terikatnya.
seperti contoh di atas, maka :
Turunan dilambangkan dengan dy/dx dan fungsi yang tidak diketahui diwakili dengan variabel y.

4. 4
Pendahuluan Cont.
22
' yxy +=
Kategorikan : (PD / bukan PD / PDP / PDB ?)
02 2
=−+ yyx
dx
dy
)2(3)(''' xSinyxCosyy =−+
''1'2'''2 yyy −=−
2
2
2
2
2
)1()(3
y
u
x
x
u
txSin
t
u
∂
∂
++
∂
∂
++=
∂
∂
4)(' 2
−=−− xxxf
)(;173' 53
tfytty =+−= −
1. PDB orde 1
2. PDP
3. Bukan PD
4. PDB orde 2
5. PDB orde 3
6. Bukan PD
7. PDP
8. PDB orde 1
yx
xye
y
u
x
u +
=
∂
∂
+
∂
∂
62
2
2
2

5. 5
Pendahuluan (Cont.)
 Solusi PDB :
– solusi analitik : salah satunya dengan teknik integral
– solusi numerik : menggunakan metode hampiran.
 Solusi Numerik :
mencari nilai fungsi di xr+1, dimana r menunjukkan
jumlah langkah atau iterasi.
 Langkah/iterasi memiliki jarak yang sama (h)
xr = x0 +rh; r = 0,1,2,…,n

6. 6
PDB Orde Satu
 Bentuk baku PDB orde satu :
 Contoh :
 Metode penyelesaian :
– Euler
– Heun
– Runge Kutta
),(')(' yxfyxf
dx
dy ===
y
x
yxyyyyy
x
yxy
xy
yyxyy
++−=→−=−=+−
−
=→==+
2'1)1(;'2
2
100
'1)0(;100'2

7. 7
Metode Euler
 Bentuk baku :
 Penurunan
– Deret Taylor : uraikan y(xr+1) disekitar xr
– Dipotong sampai orde 3 :
– Karena y’(xr) = f(xr,yr) dan xr+1-xr = h, maka :
rhxx
xyy
yxyyxfyxf
dx
dy
r
rr
+=
=
====
0
00
)(
)();,(')('
...)(''
!2
)(
)('
!1
)(
)()(
2
11
1 +
−
+
−
+= ++
+ r
rr
r
rr
rr xy
xx
xy
xx
xyxy
1
2
11
1 );(''
!2
)(
)('
!1
)(
)()( +
++
+ ≤≤
−
+
−
+= rr
rr
r
rr
rr xtxty
xx
xy
xx
xyxy
nrhOyxhfxyxy rrrr ,...,2,1,0);(),()()( 2
1 =++≈+

8. 8
Metode Euler (Cont.)
 Penurunan secara geometris :
f(x,y) adalah persamaan differensial yang dapat
digambarkan sebagai gradien garis singgung di titik
(x,y).
 Garis singgung ditarik menyinggung titik (x0,y0) untuk
menemukan nilai y(x1), pada titik (x1,y1) ditarik lagi
garis yang menyinggung titik tersebut dengan fungsi
f(x,y) untuk mendapatkan f(x2) dan seterusnya.

9. 9
0
1
2
3
4
5
6
7
8
0 0.5 1 1.5 2 2.5 3 3.5 4
y(x)
dy/dx
(x1,y1)
(x0,y0)
(x2,y2)
(x3,y3)
(x4,y4)
(x5,y5)
(x6,y6)
(x7,y7) (x8,y8)
Metode Euler (Cont.)

10. 10
0
1
2
3
4
5
6
7
0 0.5 1
y(x)
yr
Yr+1
sejati
Yr+1
hampiran
Yr
sejati
A
B
C
galat
h
),(
),(
),()('
1
1
1
rrrr
rrrr
rr
rrr
yxhfyy
yyyxhf
h
yy
AB
BC
x
y
yxfxym
+=
−=
−
==
∆
∆
===
+
+
+
Metode Euler (Cont.)

11. 11
Metode Euler (Cont.)
 Galat
– Galat Pemotongan
sebanding dengan kuadrat ukuran langkah
– Galat Kumulatif
)()(''
2
1 22
hOtyhEp =≈
)(
2
)('')(
)(''
2
)(
)(''
2
)(''
2
1 2
2
2
1
hO
thyab
tyh
h
ab
yy
nh
tyhE
n
r
kumulatif =
−
=
−
==≈ ∑=

12. 12
Metode Euler (Cont.)
 Contoh Soal :
1. dy/dx =x + y ; y(0) = 0
Berapa y(0.1) dengan langkah h = 0.02 dan h = 0.05
jika diketahui fungsi asli adalah y(x) = ex
-x-1, langkah mana yang lebih teliti ?
h = 0.05
x = 0 y(0) = 0
x = 0.05 y(0.05) = 0 + 0.05(0+0) = 0
x = 0.1 y(0.1) = 0 + 0.05(0.05+0) = 0.0025
h = 0.02
x = 0 y(0) = 0
x = 0.02 y(0.02) = 0 + 0.02(0+0) = 0
x = 0.04 y(0.04) = 0 + 0.02(0.02+0) = 0.0004
x = 0.06 y(0.06) = 0.004 +0.02(0.04+0.004) = 0.001208
x = 0.08 y(0.08) = 0.001208 +0.02(0.06+0.001208) = 0.00243216
x = 1 y(0.1) = 0.00243216 + 0.02(0.08+0.00243216) = 0.0040808032
y(0.1) = e0.1
-0.1-1 =
Langkah h = 0.02 lebih teliti
0.00517091807564762

13. 13
Metode Heun
 Merupakan perbaikan metode Euler.
 Solusi Euler dijadikan solusi perkiraan awal
dan diperbaiki dengan metode Heun.
 Perbaikan gradien yang digunakan
merupakan rata-rata gradien dari 2 titik yang
ada.

14. 14
Metode Heun (Cont.)
 Dari satu titik awal (xr,yr), iterasi dan
gradien didapatkan perkiraan nilai
y(xr+1) selanjutnya (xr+1,yr+1)
beserta gradiennya.
 Dari dua gradien yang ada dicari
rata-ratanya kemudian digunakan
untuk menghitung kembali nilai
y(xr+1).
 Misal :
– Awal iterasi dimiliki (x0,y0) dan
f(x0,y0)
– Kemudian digunakan untuk
menghitung y(x1) dan didapatkan
f(x1,y1)
– Hitung kembali y(x1) dengan gradien
(f(x0,y0)+f(x1,y1)/2
),(
)),(),((
2
1
,(
),();,(
),(
),();,(
1
0
11)
0
11
0
11
0
1
rrrr
rrrrrr
rrrr
rrrr
rrrr
yxfhyy
yxfyxfyxf
yxfyx
yxhfyy
yxfyx
+=
+=
+=
+
++
++++
+

15. 15
Metode Heun (Cont.)
 Secara geometris :
0
1
2
3
4
5
6
7
0 0.5 1
y(x)
yr_euler
yr_heun
f(xr,yr) f(xr+1,yr+1)
frat(xr,yr)
(xr,yr)
(xr+1,yr+1)

16. 16
Metode Runge Kutta
 Bentuk umum Runge Kutta Orde n:
yr+1 = yr + a1k1 + a2k2 + … + ankn
Dengan a1,a2,a3, …,an adalah konstanta
k1 = hf(xr,yr)
k2 = h(f(xr+p1h, yr+q11k1)
k3 = h(f(xr+p2h,yr+q21k1+q22k2)
k4 = h(f(xr+p3h,yr+q31k1+q32k2+q33k3)
…
kn = h(xr+pn-1h,yr+qn-1,1k1+qn-1,2+…+qn-1,n-1kn-1)
 Galat
– Per langkah Runge Kuta orde –n : O(hn+1
)
– Kumulatif orde-n :O(hn
)

17. 17
 Orde 1
k1 = hf(xr,yr)
yr+1 = yr + a1k1 ; a1 = 1
yr+1 = yr + hf(xr,yr)  Rumus Euler
Galat :
Per langkah : O(h2
)
Kumulatif : O(h)
Metode Runge Kutta (Cont. )

18. 18
 Orde 2
k1 = hf(xr,yr)
k2 = h(f(xr+p1h, yr+q11k1)
yr+1 = yr + a1k1 + a2k2
Dengan penurunan rumus yang sudah ada didapatkan :
a1 = 1-a2 = 1-t
p1 = 1/(2a2) = 1/(2t)
q11 = 1/(2a2) = 1/(2t)
Artinya ada tak berhingga formula orde dua.
Dengan a1=a2 = ½, p1 = 1
yr+1 = yr + ½ (k1 + k2)  Metode Heun
Metode Runge Kutta (Cont. )

19. 19
 Orde 3
k1 = hf(xr,yr)
k2 = h(f(xr+p1h, yr+q11k1)
k3 = h(f(xr+p2h,yr+q21k1+q22k2)
yr+1 = yr + a1k1 + a2k2 + a3k3
dengan menggunakan penurunan rumus yang ada
didapatkan :
k1 = hf(xr,yr)
k2 = h(f(xr+1/2 h, yr+1/2 k1)
k3 = h(f(xr+h,yr-k1+2k2)
yr+1 = yr + 1/6( k1 + 4k2 + k3)
Metode Runge Kutta (Cont. )

20. 20
 Orde 4
k1 = hf(xr,yr)
k2 = h(f(xr+p1h, yr+q11k1)
k3 = h(f(xr+p2h,yr+q21k1+q22k2)
k4 = h(f(xr+p3h,yr+q31k1+q32k2+q33k3)
yr+1 = yr + a1k1 + a2k2 + a3k3 + a4k4
dengan menggunakan penurunan rumus yang ada
didapatkan :
k1 = hf(xr,yr)
k2 = h(f(xr+1/2 h, yr+1/2 k1)
k3 = h(f(xr+1/2h,yr+2k2)
k4 = h(f(xr+h,yr+k3)
yr+1 = yr + 1/6( k1 + 2k2 + 2k3 + k4)
Metode Runge Kutta (Cont. )