1. Model matematis sistem mewakili hubungan input dan output sistem melalui persamaan matematis. 2. Transfer function menjelaskan hubungan antara transformasi Laplace dari input dan output sistem. 3. Blok diagram dan signal flow graph digunakan untuk merepresentasikan model matematis sistem secara visual.

1. MODEL-MODEL MATEMATIS DARI SISTEM-SISTEM FISIS
Model matematis suatu sistem :
Persamaan matematis yang menunjukan hubungan input dan output dari suatu sistem
yang bersangkutan.
Dengan mengteahui model matematis ini, maka kita dapat menganalisa tingkah laku sistem.
Sistem
INPUT OUPUT
R(s) C(s)
Diagram diatas menunjukan diagram model matematis suatu sistem.
R(s) = transformasi Laplace dari input
C(s) = transformasi Laplace dari output
G(s) = transformasi Laplace dari hubungan input dan output dari sistem.
C(s) = G(s).R(s)
 Transfer function : )(
)(
)(
sG
sR
sC

model matematis sistem ekuivalen dengan transfer function.
Transfer function / fungsi alih :
Perbandingan antara transformasi laplace dari output dengan transformasi laplace dari
inputnya, dengan anggapan semua kondisi awal = 0.
1. F = input (gaya) ; x = output (pergeseran)
k = konstanta pegas
m = massa f
= koefisien gesekan (piston)
carilah transfer function sistem mekanis diatas !
Solusi :
F = m.a
F – k.x – f.
.
x = m.
..
x
F(s) – kX(s) – fsX(s) = ms2X(s)
F(s) = (ms2 + fs + k) X(s)
kfs2ms
1
F(s)
X(s)


1.
G(s)

2. J = momen inersia
f = koefisien gesek
 = kecepatan sudut (output)
T = torsi (input)
 = percepatan sudut
 = pergeseran sudut
J = T
J
.
ω = T-f.
Js(s) = T(s) – f(s)
T(s) = (Js +f) (s)
fJs
1
T(s)
Ω(s)


eI =  i.dt
c
1
R.i
dt
di
L. ………………(1)
e0 = i.dt
c
1
………………(2)
Transformasi Laplace :
1 EI(s) = Ls I(s) + R I(s) + I(s)
Cs
1
2 E0(s) = I(s)
Cs
1
 I(s) = C s E0(s)
21:
EI(s) = L C s2 E0(s) + R C E0(s) + E0(s)
EI(s) = C L C s2 + R (s +1) E0(s)
1RCs2LCs
1
(s)
i
E
(s)
0
E



3. 1RCs
1
(s)
i
E
(s)
0
E

 (Buktikan !!!)
Bila kedua rangkaian RC
disamping tidak dianggap
terpisah.
EI = R1.i1 +   )dt
2
i
1
(i ………………… (1)
0 =   .dt
2
i
2
C
1
2
.i
2
R)dt
1
i
2
(i
1
C
1
………..(2)
e0 =  .dt
2
i
2
C
1
………………….(3)
Transformasi Laplace :
1 (s))
2
I(s)
1
(I
(s)
1
C
1
1
.i
1
R(s)
i
E 
2 (s)
2
I
s
2
C
1
(s)
2
.I
2
R(s))
1
I(s)
2
(I
s
1
C
1
0 
3 (s)
2
I
s
2
C
1
(s)
0
E 
Eliminasi I1(s) dan I2(s) dari ketiga persamaan diatas menghasilkan :
1)s
2
C
1
R
2
C
2
R
1
C
1
(R2s
2
C
2
R
1
C
1
R
1
(s)
1
E
(s)
0
E


Bila Kedua rangkaian RC diatas dianggap terpisah.

4. 1s
1
C
1
R
1
(s)
i
E
(s)
m
E


1s
2
C
2
R
1
(s)
i
E
(s)
m
E


Transfer Function :
1s
1
C
1
R
1
.
1s
2
C
2
R
1
(s)
i
E
(s)
m
E
.
(s)
m
E
(s)
0
E
(s)
i
E
(s)
0
E


1)s
2
C
2
R
1
C
1
(R2s
2
C
2
R
1
C
1
R
1


X1(s) X2(s) X3(s) X

X1(s) X3(s)
(s)
2
X
(s)
3
X
(s)
2
G,
(s)
1
X
(s)
2
X
(s)
1
G 
(s)
2
(s).G
1
G
(s)
2
X
(s)
3
X
.
(s)
1
X
(s)
2
X
(s)
1
X
(s)
3
X
G(s) 
)
1s
2
C
2
R
1
)(K)(
1s
1
C
1
R
1
(
(s)
i
E
(s)
0
E


1)s
2
C
2
1)(Rs
1
C
1
(R 

K
BLOK DIAGRAM (DIAGRAM KOTAK)
Blok diagram : Suatu pernyataan grafis untuk menggambarkan sistem pengaturan.
Elemen-elemen blok diagram :
G1(s) G2(s)
G1(s) G2(s)

5. a. PROSES atau TRANSFER FUNCTION
b. ELEMEN PENJUMLAHAN
A C C = A - B
B
c. PERCABANGAN
BLOK DIAGRAM LENGKAP UNTUK SISTEM SEDERHANA :
R(s) = input
C(s) = output
G(s) = transfer function “feedforward”
H(s) = transfer function “feedback”
G(s)H(s) = transfer function “open-loop”
Transfer function “closed-loop” :
E(s) = R(s) – B(s) ………..(1)
B(s) = C(s) . H(s) ………. (2)
C(s) = E(s) . G(s) ………..(3)
21 : E(s) = R(s) – C(s).H(s) ……..(4)
43 : C(s) = (R(s) – C(s).H(s)) G(s)
C(s) + G(s)H(s)C(s) = G(s)R(s)

G(s)H(s)1
G(s)
R(s)
C(s)


Contoh :
TRANSFER
FUNCTION G(s)

6. (s)H(s)
2
(s)G
1
G1
(s)
2
(s)G
1
G
R(s)
C(s)


SISTEM CLOSED-LOOP (SISTEM TERTUTUP) DENGAN DISTURBANSI :
N(s) = Disturbance
a. N(s) = 0
(s)H(s)
2
(s)G
1
G1
(s)
2
(s)G
1
G
R(s)
C(s)


R(s)
(s)H(s)
2
(s)G
1
G1
(s)
2
(s)G
1
G
C(s)


b. R(s) = 0

7. Atau
(s).H(s)
2
(s)G
1
G1
(s)
2
G
N(s)
C(s)


N(s)
(s).H(s)
2
(s)G
1
G1
(s)
2
G
C(s)


 output total :
N(s)
(s)H(s)
2
(s)G
1
G1
(s)
2
G
R(s)
(s)H(s)
2
(s)G
1
G1
(s)
2
(s)G
1
G
C(s)




BLOK DIAGRAM SISTEM FISIS :
EI = R.i + i.dt
C
1
.…. (1)
E0 = i.dt
C
1
….. (2)
Transformasi Laplace :
1 EI(s) = RI(s) + I(s)
Cs
1
2 E0(s) = I(s)
Cs
1
21 : EI(s) = RI(s) + E0(s)
RI(s) = EI(s) – E0(s)

8. I(s) =
R
(s)
0
E(s)
i
E 
BLOK DIAGRAM PERSAMAAN : I(s) =
R
(s)
0
E(s)
i
E 
BLOK DIAGRAM PERSAMAAN : E0(s) = I(s)
Cs
1
I(s) E0(s)
BLOK DIAGRAM RANGKAIAN RC
Atau :
RCs1
1
1/RCs1
1/RCs
(s)
i
E
(s)
0
E




ATURAN PENYEDERHANAAN BLOK DIAGRAM
Cs
1

9. Contoh : Hitung
R(s)
C(s)
u/ sistem yang mempunyai blok diagram sebagai berikut :

10. MENDAPATKAN TRANSFER FUNCTION DARI SISTEM FISIS
1 MOTOR DC DENGAN PENGATURAN JANGKAR

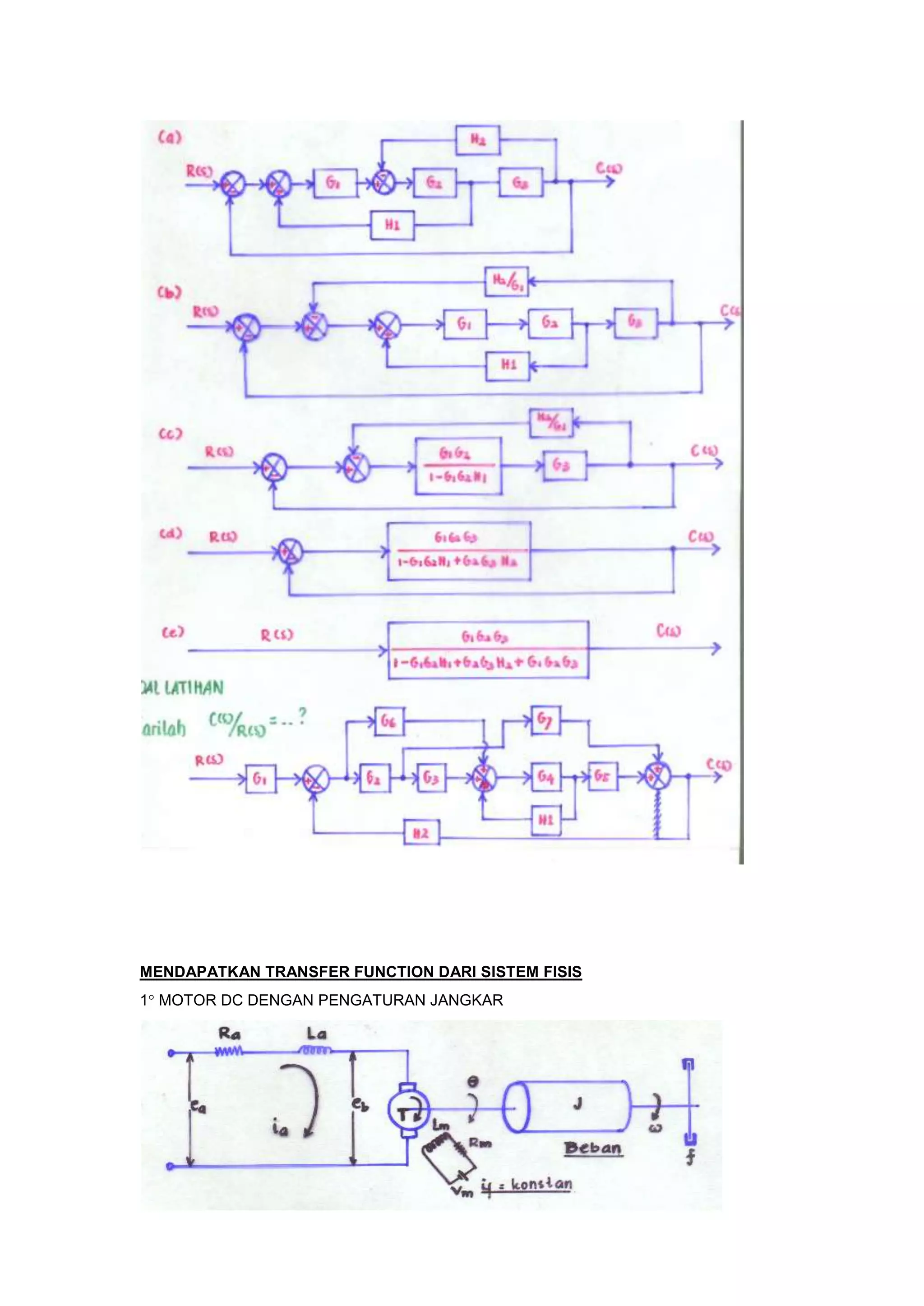
11. Ra = tahanan jangkar
La = induktansi jangkar
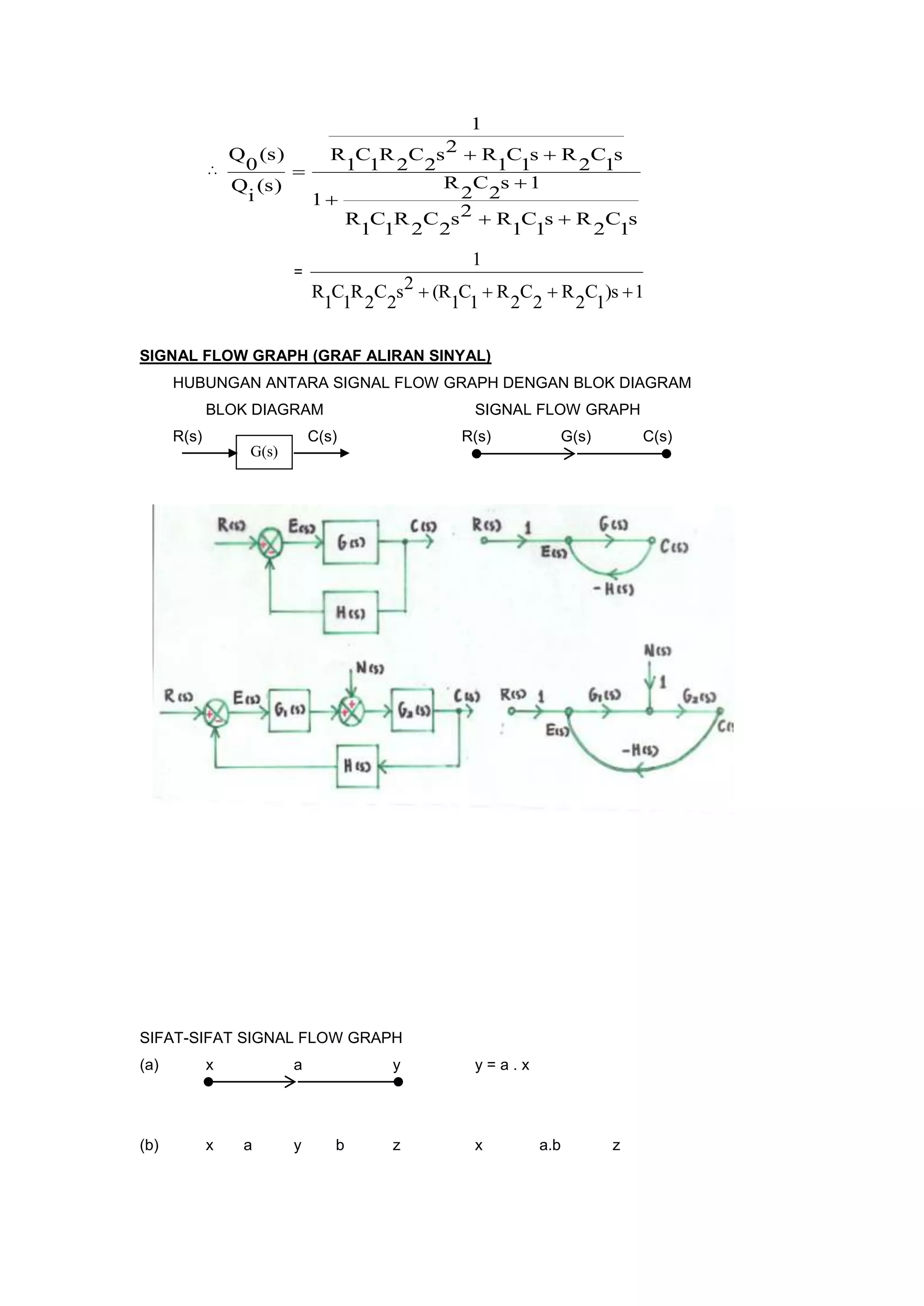
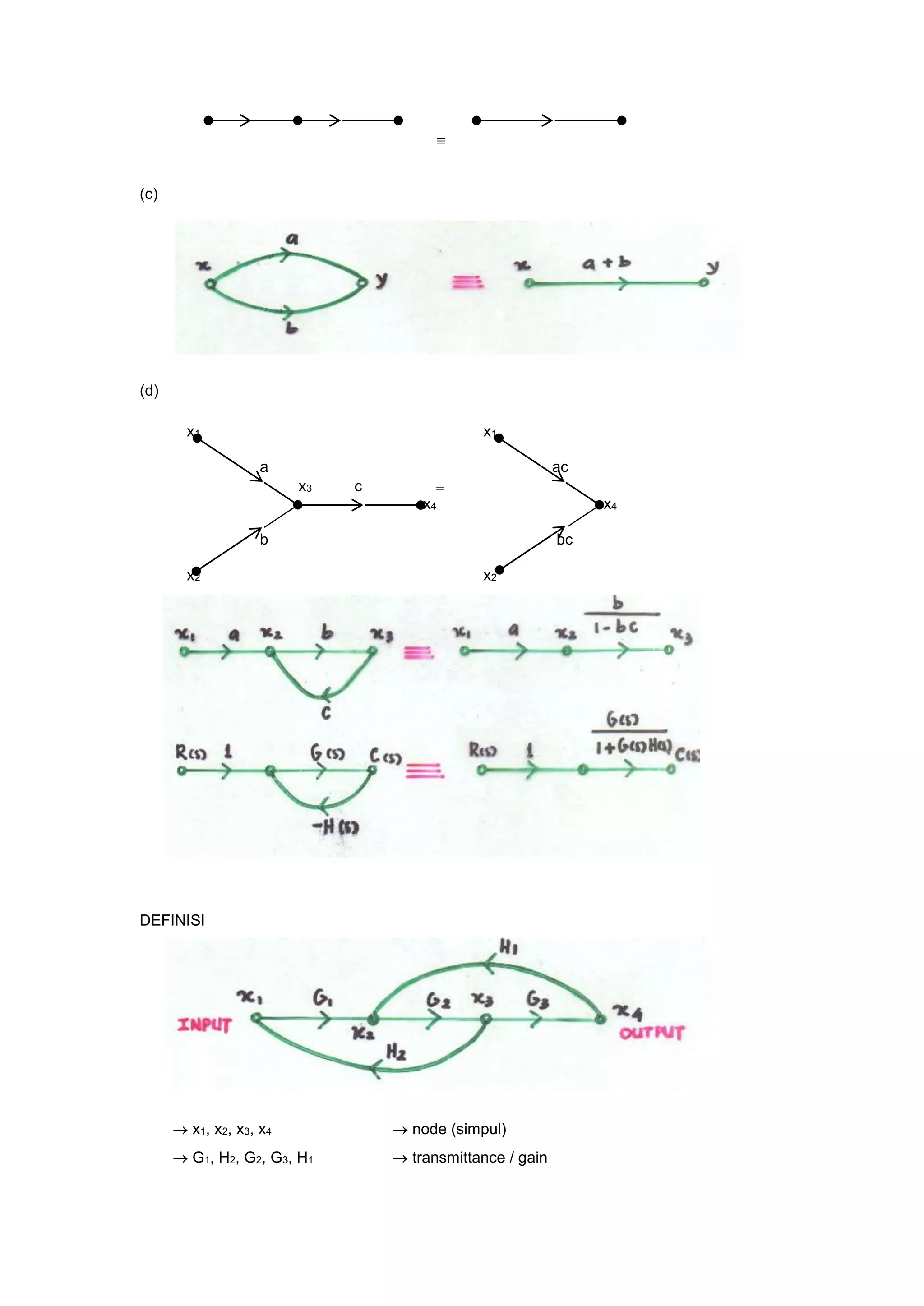
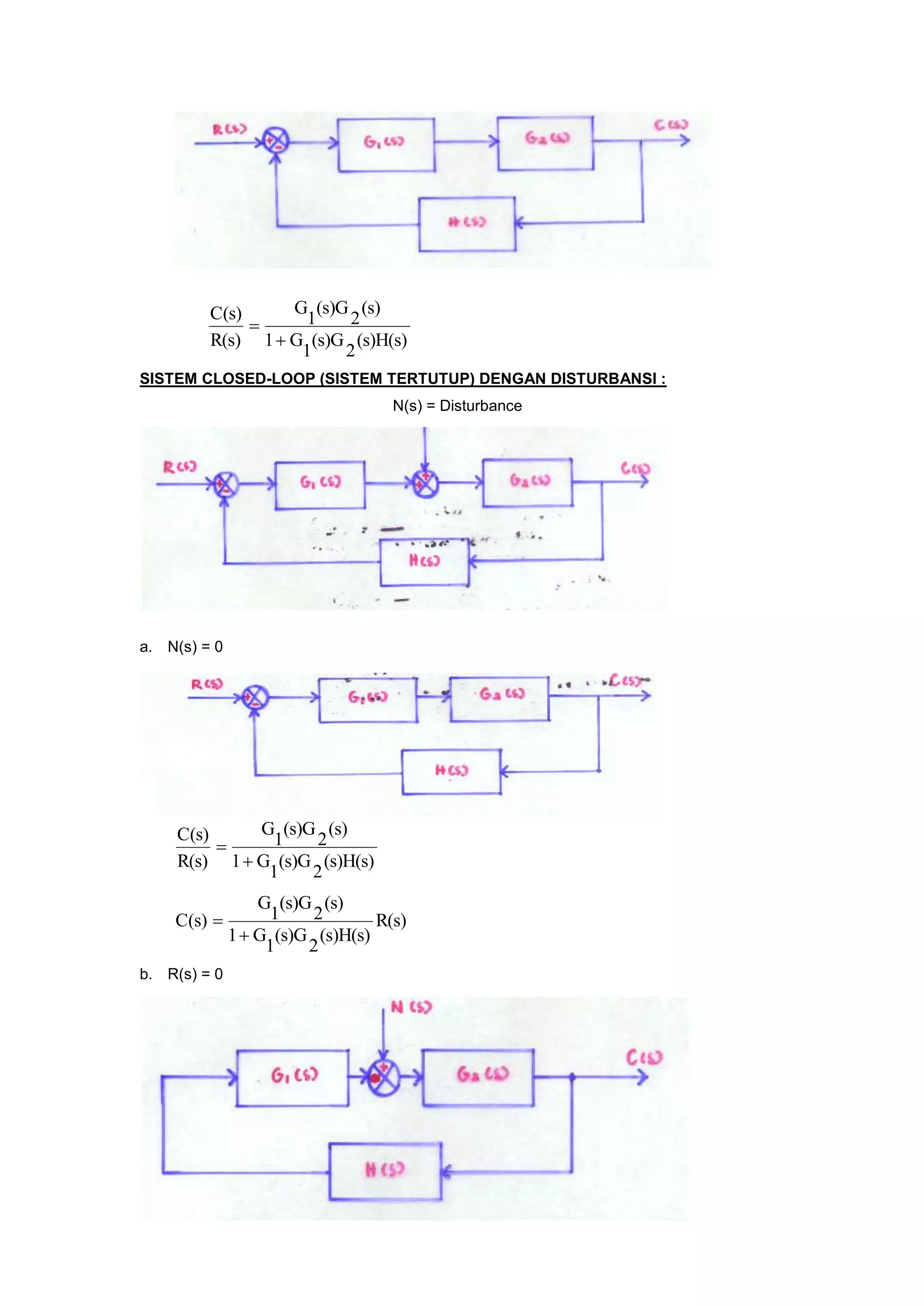
ia = arus jangkar
if = arus medan
ea = tegangan jangkar
eb = emf terinduksi
 = perpindahan sudut dari poros / batang meter
T = torsi
J = momen inersia total
f = koefisien geseran total
Persamaan Sistem :
(1) ea = Ra.ia + La.
b
e
dt
a
di

(2) eb = K . n .  = c . n = c . 
(3) T = KI .  . Ia = cI . ia
(4) J.
.
ω + f .  = T
......?
(s)
a
E
Ω(s)

Transformasi Laplace :
(1) Ea(s) = Ia(s) [Ra + La . s] + Eb(s)
(2) Eb(s) = c . (s)
(3) T(s) = CI.Ia(s)
(4) T(s) = (s) [Js +f]
(1) Ia(s) [Ra + Las] = Ea(s) – Eb(s)
(2) Eb(s) = c . (s)
(s) Eb(s)
(3) T(s) = cI . Ia(s)
C

12. fJs
1

Ia(s) T(s)
(4) (s) =
fJs 
1
T(s)
(s)T(s)
Blok Diagram Sistem :

)
1
ccf
a
(RJ)s
a
Rf
a
(L2Js
a
L
1
c
(s)
a
E
Ω(s)


2 SISTEM LEVEL CAIRAN
A)
qI = aliran air yg masuk
q0 = aliran air yang keluar
R = tahanan kran
C = kapasitas tangki
h = tinggi air
(1) h = q0 . R  H(s) = R Q0(s)
CI

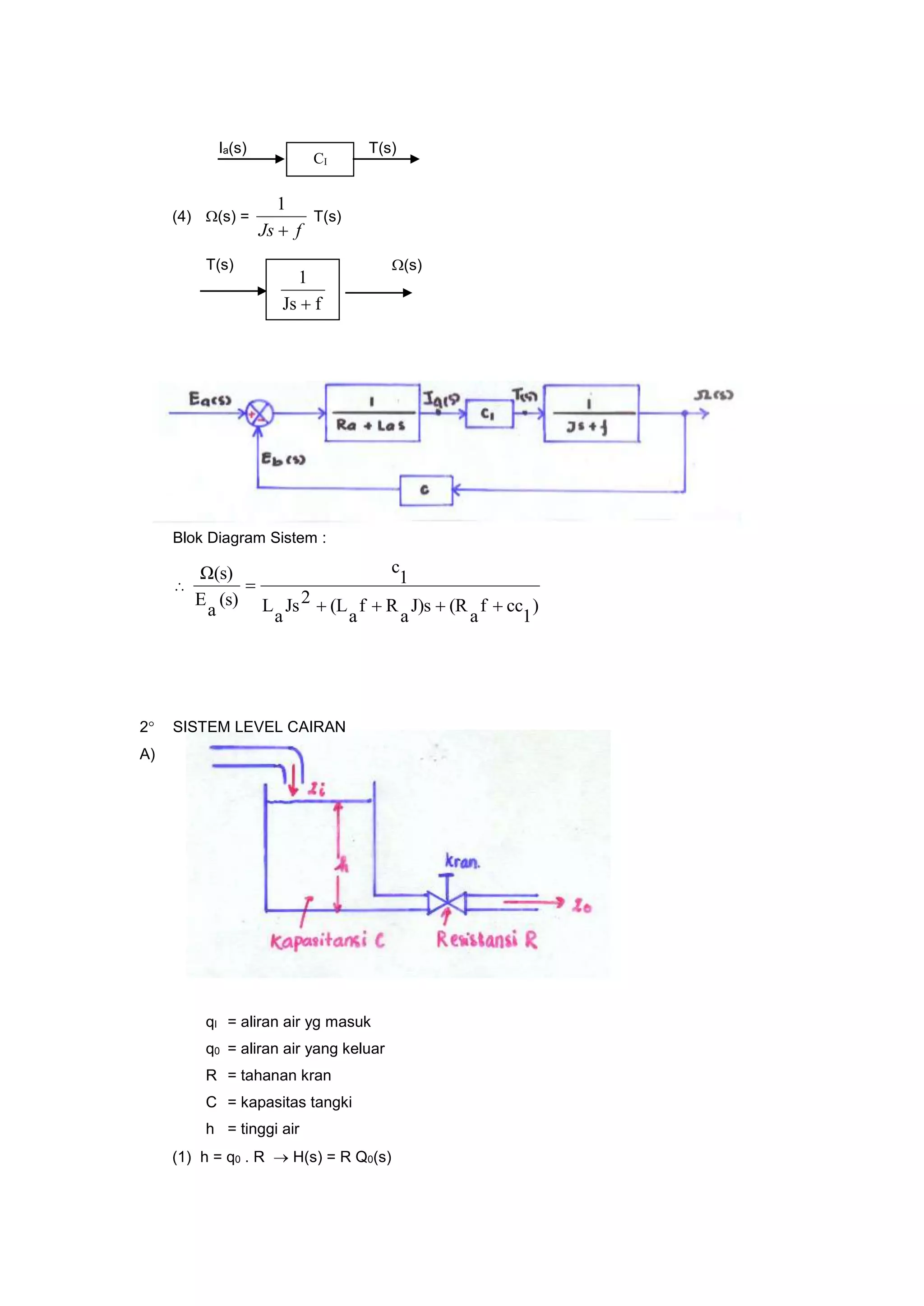
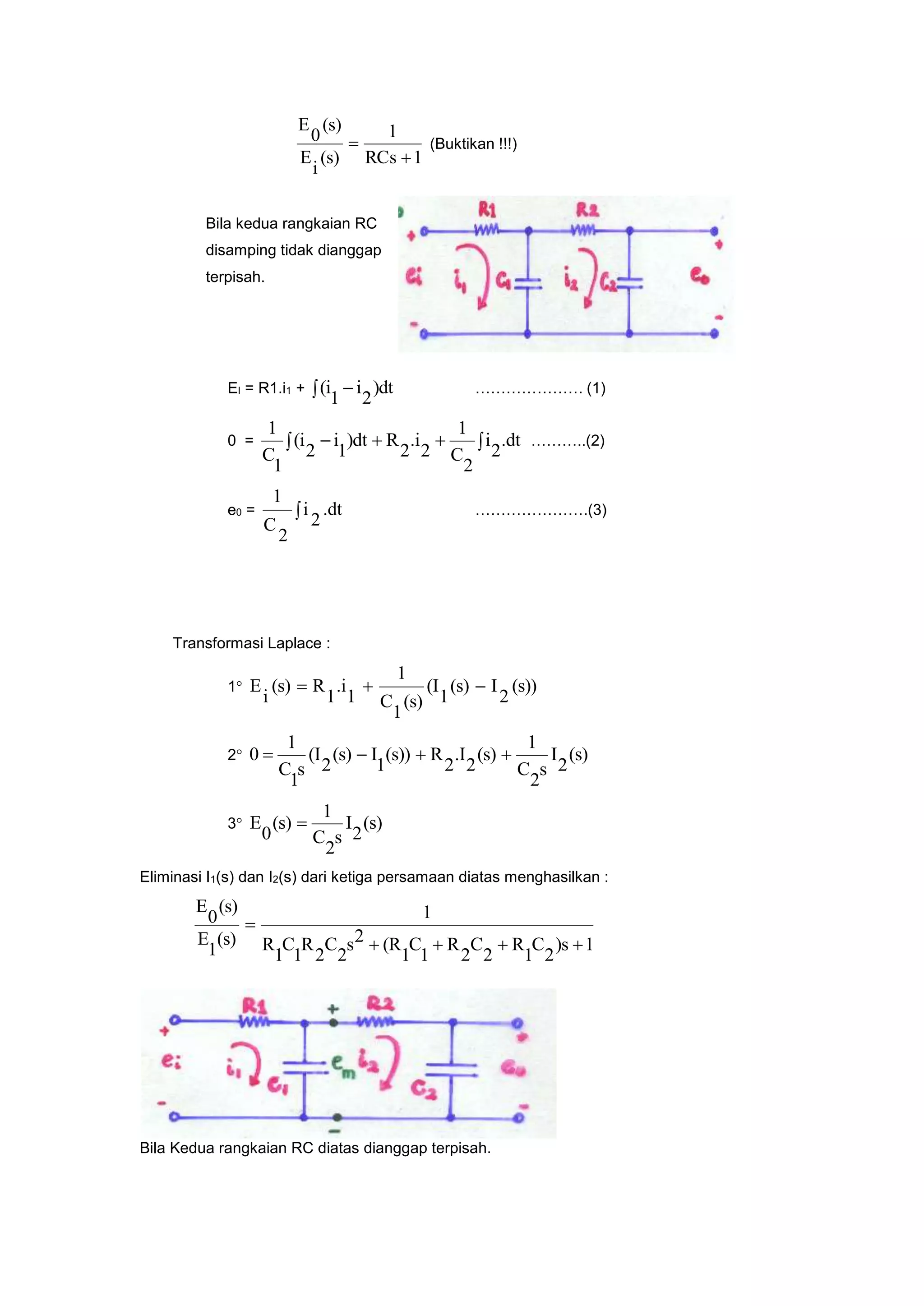
13. (2)
0
q
i
q
dt
dh
C   C.sH(s) = QI(s) – Q0(s)
.....?
(s)
i
Q
H(s)

H(s) = R [QI(s) – CsH(s)]
[RC.s + 1] H(s) = RQi(s)]

1)R(s
R
(s)
i
Q
H(s)


B)
......?
(s)
i
Q
(s)
0
Q

Tangki 2 :
q0 =
2
R
2
h
 Q0(s) =
2
R
(s)
2
H
…. (1)
C2
dt
2
dh
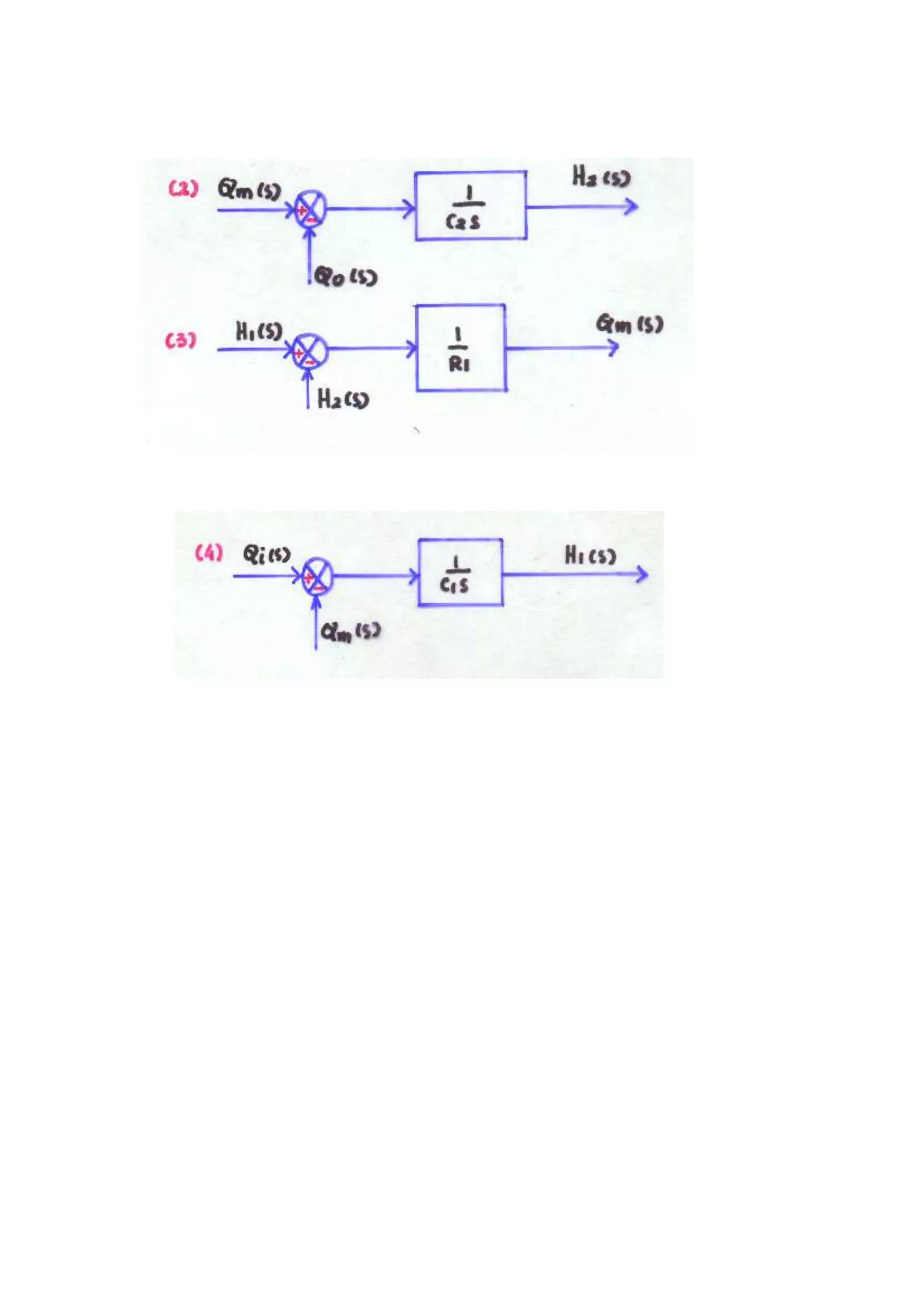
= qm – q0  C2sH2(s) = Qm(s) – Q0(s) ….(2)
Tangki 1 :
(s)....(4)
m
Q(s)
i
Q(s)
1
sH
1
C
m
q
1
q
dt
1
dh
1
C
.....(3)
1
R
(s)
2
H(s)
1
H
(s)
m
Q
1
R
2
h
1
h
m
q





(1) H2(s) Q0(s)
2
R
1

15. Penggabungan :

16. 
s
1
C
2
Rs
1
C
1
R2s
2
C
2
R
1
C
1
R
1s
2
C
2
R
1
s
1
C
2
Rs
1
C
1
R2s
2
C
2
R
1
C
1
R
1
(s)
i
Q
(s)
0
Q





=
1)s
1
C
2
R
2
C
2
R
1
C
1
(R2s
2
C
2
R
1
C
1
R
1

SIGNAL FLOW GRAPH (GRAF ALIRAN SINYAL)
HUBUNGAN ANTARA SIGNAL FLOW GRAPH DENGAN BLOK DIAGRAM
BLOK DIAGRAM SIGNAL FLOW GRAPH
R(s) C(s) R(s) G(s) C(s)
SIFAT-SIFAT SIGNAL FLOW GRAPH
(a) x a y y = a . x
(b) x a y b z x a.b z
G(s)

17. 
(c)
(d)
DEFINISI
 x1, x2, x3, x4  node (simpul)
 G1, H2, G2, G3, H1  transmittance / gain
x1 x1
a ac
x3 c 
x4 x4
b bc
x2 x2

18.  x1  input node (source)
 x4  output node (sink)
 x2, x3  mixed node
 G1 G2 G3 = gain lintasan maju / kedepan (forward path gain)
 Gain lintasan tertutup :
G1, G2, H2 / G2, H2, G1
G2, G3, H1
 Dua atau lebih lintasan tertutup dikatakan tidak bersentuhan bila lintasan-lintasan tersebut
tidak melintasi suatu transmittance yang sama.
Contoh :
Gain lintasan maju : 1) G1 G2 G3 G4 G5
2) G1 G2 G6 G5
gain lintasan tertutup : 1) G1 G2 H1 3) G4 G5 H3
2) G2 G3 H2 4) G2 G6 G5 H3 H2
TEORI MASON
P = fungsi alih / tranfer function total
 = ....
kj,i,
k
L
j
L
i
L
ji,
j
L
i
L
i
i
L1 
PI = gain / transmittance lintasan maju ke I
LiLj = gain total dari dua buah lintasan tertutup yang tidak saling bersinggungan
LiLjLk = gain total dari tiga buah lintasan tertutup yang tidak saling bersinggungan
I =  bila lintasan maju ke i dihilangkan, atau bila lintasan-lintasan tertutup yang
menyentuh lintasan maju ke i dihilangkan
Contoh :
P1 = G1 G2 G3 G4 G5

i
i
Δ
i
P
Δ
1
P
R(s)
C(s)

19. P2 = G1 G2 G5 G6
L1 = G1 G2 H1 L3 = G4 G5 H3
L2 = G2 G3 H2 L4 = G2 G5 G6 H2 H3
Dua buah lintasan tertutup yang tidak bersinggungan
L1 L3 = G1 G2 G4 G5 H1 H3
L2 L3 = G2 G3 G4 G5 H2 H3
 = 1 – L1 – L2 – L3 – L4 + L1 L3 + L2 L3
1 = 1
2 = 1
32543231542132652354232121
652154321
32314321
2211
HHGGGGHHGGGGHHGGGHGGHGGHGG1
GGGGGGGGG
R(s)
C(s)
LLLLLLLL1
ΔPΔP
P
R(s)
C(s)






soal latihan :