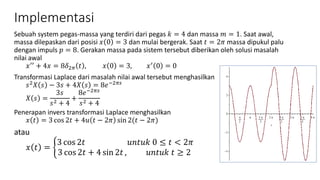
Dokumen tersebut membahas tentang transformasi Laplace dan beberapa fungsi dasar yang terkait dengan transformasi Laplace seperti fungsi tangga, fungsi periodik, dan impuls. Secara singkat, dokumen tersebut memberikan definisi transformasi Laplace dan rumus-rumus dasar serta contoh penerapannya dalam menyelesaikan masalah nilai awal dan masalah diferensial biasa.

1. Transformasi Laplace
(Bag 2)
Mata Kuliah
Persamaan Diferensial Biasa
Rabu, 7 November 2018

2. Fungsi Tangga Satuan
DEFINISI 1.
Fungsi Tangga satuan (unit step function) didefinisikan sebagai
𝑢 𝑎 𝑡 = 𝑢 𝑡 − 𝑎 =
0, 𝑢𝑛𝑡𝑢𝑘 𝑡 < 𝑎
1, 𝑢𝑛𝑡𝑢𝑘 𝑡 ≥ 𝑎
Fungsi 𝑢 𝑡 − 𝑎 seolah-olah seperti tombol switch on yang mulai
dinyalakan saat 𝑡 = 𝑎.
Perhatikan bahwa
𝑢 𝑎 𝑡 ℎ 𝑡 = 𝑢 𝑡 − 𝑎 ℎ 𝑡 =
0, 𝑢𝑛𝑡𝑢𝑘 𝑡 < 𝑎
ℎ(𝑡), 𝑢𝑛𝑡𝑢𝑘 𝑡 ≥ 𝑎

3. Grafik beberapa fungsi tangga
𝐜𝐨𝐬 𝟐𝒕 (𝒖 𝒕 − 𝝅 − 𝒖(𝒕 − 𝟑𝝅))
𝑢(𝑡)𝑢(𝑡 − 𝜋)𝒕𝒖 𝒕 − 𝝅
𝒔𝒊𝒏(𝒕) 𝟏 − 𝒖(𝒕 − 𝝅)

4. 1. Tunjukkan bahwa
ℒ 𝑢0 𝑡 =
1
𝑠
untuk 𝑠 > 0
2. Tunjukkan bahwa
ℒ 𝑢 𝑎 𝑡 =
𝑒−𝑎𝑠
𝑠
, 𝑢𝑛𝑡𝑢𝑘 𝑠 > 0 𝑑𝑎𝑛 𝑎 > 0
Contoh soal (1)

5. PROPOSISI 2 (Translasi sepanjang sumbu-𝑡)
Jika 𝐹 𝑠 = ℒ(𝑓(𝑡)) untuk 𝑠 > 𝑐, maka
ℒ 𝑢 𝑡 − 𝑎 𝑓 𝑡 − 𝑎 = 𝑒−𝑎𝑠 𝐹 𝑠 , untuk 𝑠 > 𝑐 + 𝑎
BUKTI :
𝑒−𝑎𝑠 𝐹 𝑠 = 𝑒−𝑎𝑠
0
∞
𝑒−𝑠𝑡 𝑓 𝑡 𝑑𝑡 =
0
∞
𝑒−𝑠 𝑡+𝑎 𝑓(𝑡) 𝑑𝑡
Substitusi 𝜏 = 𝑡 + 𝑎 menghasilkan
𝑒−𝑎𝑠
𝐹 𝑠 =
𝑎
∞
𝑒−𝑠𝜏
𝑓 𝜏 − 𝑎 𝑑𝜏 =
𝑎
∞
𝑒−𝑠𝜏
𝑢(𝜏 − 𝑎)𝑓 𝜏 − 𝑎 𝑑𝜏

6. LATIHAN SOAL
1. Tentukan ℒ−1 𝑒−𝑎𝑠
𝑠3 !
2. Tentukan ℒ{𝑔(𝑡)} jika diketahui
𝑔 𝑡 =
0, 𝑗𝑖𝑘𝑎 𝑡 < 3
𝑡2, 𝑗𝑖𝑘𝑎 𝑡 ≥ 3
3. Tunjukkan bahwa jika
𝑓 𝑡 =
cos 2𝑡, 𝑗𝑖𝑘𝑎 0 ≤ 𝑡 < 2𝜋
0, 𝑗𝑖𝑘𝑎 𝑡 ≥ 2𝜋
maka 𝐹 𝑠 =
𝑠(1−𝑒−2𝜋𝑠)
𝑠2+4
4. Sebuah sistem yang terdiri dari pegas (𝑘 = 4 𝑙𝑏/𝑓𝑡) dan massa (𝑚 = 32 𝑙𝑏)
mula-mula berada dalam kondisi diam. Pada saat awal 𝑡 = 0, massa dikenai
gaya luar sebesar 𝑓 𝑡 = cos 2𝑡 dan pada 𝑡 = 2𝜋 gaya seketika dihentikan.
Jika 𝑥(𝑡) menyatakan simpangan massa dari posisi setimbang saat 𝑡,
tentukan 𝑥(𝑡). Bagaimanakah gerak sistem untuk 𝑡 → ∞?

7. TEOREMA 3 : (Translasi sepanjang sumbu-𝑠)
Jika 𝐹 𝑠 = ℒ{𝑓(𝑡)} untuk 𝑠 > 𝑐, maka
ℒ 𝑒 𝑎𝑡
𝑓 𝑡 = 𝐹(𝑠 − 𝑎), untuk 𝑠 > 𝑎 + 𝑐
Dengan menggunakan teorema di atas diperoleh rumus berikut
1. ℒ 𝑒 𝑎𝑡 𝑡 𝑛 =
𝑛!
(𝑠−𝑎) 𝑛+1 , 𝑠 > 𝑎
2. ℒ 𝑒 𝑎𝑡 cos 𝑘𝑡 =
𝑠−𝑎
(𝑠−𝑎)2+𝑘2 , 𝑠 > 𝑎
3. ℒ 𝑒 𝑎𝑡 sin 𝑘𝑡 =
𝑘
(𝑠−𝑎)2+𝑘2 , 𝑠 > 𝑎

8. CONTOH SOAL
Tunjukkan bahwa
1. ℒ−1 3𝑠+19
𝑠2+6𝑠+34
= 3𝑒−3𝑡 cos 5𝑡 + 2𝑒−3𝑡 sin 5𝑡
2. ℒ−1 𝑠2+1
𝑠3−2𝑠2−8𝑠
= −
1
8
+
5
12
𝑒−2𝑡 +
17
24
𝑒4𝑡

9. LATIHAN SOAL
1. Tentukan transformasi Laplace dari fungsi berikut
a. 𝑢1 𝑡 + 2𝑢3 𝑡 − 6𝑢4(𝑡) b. 𝑡4
𝑒 𝜋𝑡
c. 𝑡3/2
𝑒−4𝑡
d. 𝑒−2𝑡
sin 3𝜋𝑡 e. 𝑒−𝑡/2
cos 2(𝑡 − 𝜋/4)
2. Tentukan invers transformasi Laplace dari fungsi berikut
a.
2
𝑠𝑒3𝑠 b.
3𝑠+5
𝑠2−6𝑠+25
c.
𝑠2−2𝑠
𝑠4+5𝑠2+4
3. Tentukan solusi masalah nilai awal berikut
a. 𝑥′′ + 6𝑥′ + 25𝑥 = 0, 𝑥 0 = 2, 𝑥′ 0 = 3
b. 𝑥′′
+ 4𝑥′
+ 8𝑥 = 𝑒−𝑡
, 𝑥 0 = 𝑥′
0 = 0
c. 𝑥′′
+ 6𝑥′
+ 18𝑥 = cos 2𝑡 , 𝑥 0 = 1, 𝑥′
0 = −1

10. Perkalian, turunan, dan integral dari
transformasi
DEFINISI 4 .
Konvolusi dari fungsi f dan g yang kontinu bagian demi bagian, didefinisikan sebagai
𝑓 ∗ 𝑔 𝑡 =
0
𝑡
𝑓 𝜏 𝑔 𝑡 − 𝜏 𝑑𝜏 , 𝑡 ≥ 0
PROPOSISI 5.
Beberapa sifat konvolusi yakni
1. 𝑓 ∗ 𝑔 = 𝑔 ∗ 𝑓
2. 𝑓 ∗ 𝑔1 + 𝑔2 = 𝑓 ∗ 𝑔1 + 𝑓 ∗ 𝑔2
3. 𝑓 ∗ 𝑔 ∗ ℎ = 𝑓 ∗ 𝑔 ∗ ℎ
4. 𝑓 ∗ 0 = 0 ∗ 𝑓 = 0

11. PROPOSISI 6. (Transformasi Lamplace dari Konvolusi)
ℒ 𝑓 𝑡 ∗ 𝑔 𝑡 = ℒ 𝑓 𝑡 ℒ 𝑔 𝑡
⟺ ℒ−1 𝐹 𝑠 𝐺 𝑠 = 𝑓 𝑡 ∗ 𝑔(𝑡)
PROPOSISI 7. (Diferensial dari transformasi)
ℒ 𝑡𝑓 𝑡 = −𝐹′(𝑠)
⟺ 𝑡𝑓 𝑡 = −ℒ−1{𝐹′ 𝑠)}
Jika sifat pada Proposisi 7 diterapkan berulang-ulang akan diperoleh
ℒ 𝑡 𝑛 𝑓 𝑡 = −1 𝑛 𝐹 𝑛 (𝑠), untuk 𝑛 = 1,2,3, …

12. PROPOSISI 8. (Integral dari transformasi)
Jika lim
𝑡→0
𝑓(𝑡)
𝑡
ada dan transformasi Laplace dari 𝑓(𝑡) ada untuk 𝑠 > 𝑐,
maka
ℒ
𝑓(𝑡)
𝑡
= 0
∞
𝐹(𝜎) 𝑑𝜎, untuk 𝑠 > 𝑐

13. LATIHAN SOAL
1. Tunjukkan bahwa
a. ℒ 𝑡 cos 𝑘𝑡 =
𝑠2−𝑘2
(𝑠2+𝑘2)2 c. ℒ−1 1
(𝑠2+𝑘2)2 =
1
2𝑘3 sin 𝑘𝑡 − 𝑘𝑡 cos 𝑘𝑡
b. ℒ 𝑡 sinh 𝑘𝑡 =
2𝑘𝑠
(𝑠2−𝑘2)2
2. Buktikan ℒ 𝑡 sinh 𝑡 =
2𝑠
(𝑠2−1)2 dan ℒ
sin 𝑡
𝑡
= arctan
1
𝑠
!
3. Tentukan invers transformasi Laplace dari
a.
𝑒−𝜋𝑠
𝑠2+1
b. 𝐹 𝑠 =
𝑒−𝑠−𝑒−3𝑠
𝑠2 c. 𝐹 𝑠 =
𝑠𝑒−𝑠
𝑠2+𝜋2

14. 4. Tentukan transformasi Laplace dari
a. 𝑓 𝑡 =
2, 𝑗𝑖𝑘𝑎 0 ≤ 𝑡 < 3
0, 𝑗𝑖𝑘𝑎 𝑡 ≥ 3
b. 𝑓 𝑡 =
sin 𝑡, 𝑗𝑖𝑘𝑎 0 ≤ 𝑡 < 3𝜋
0, 𝑗𝑖𝑘𝑎 𝑡 ≥ 3𝜋
c. 𝑓 𝑡 =
cos
𝜋𝑡
2
, 𝑗𝑖𝑘𝑎 3 ≤ 𝑡 ≤ 5
0, 𝑗𝑖𝑘𝑎 𝑡 < 3 𝑎𝑡𝑎𝑢 𝑡 > 5
5. Hitunglah ℒ−1 ln
𝑠+1
𝑠
dengan menggunakan rumus diferensial
dan rumus integral dari transformasi !

15. Gaya luar berupa fungsi periodik
PROPOSISI 9. (Transformasi dari fungsi periodik)
Misalkan f(t) fungsi periodic dengan periode 𝑝 dan kontinu bagian demi
bagian untuk 𝑡 ≥ 0, maka transformasi 𝐹(𝑠) ada dan rumusannya
𝐹 𝑠 =
1
1 − 𝑒−𝑝𝑠
0
𝑝
𝑒−𝑠𝑡 𝑓(𝑡) 𝑑𝑡, 𝑠 > 0

16. Perhatikan fungsi gelombang persegi
berperiode 2𝑎 dengan formula
𝑓 𝑡 = (−1) 𝑡/𝑎
Transformasi Laplace dari fungsi f(t) tersebut diperoleh menggunakan
rumus transformasi fungsi periodik, sebagai berikut
𝐹 𝑠 =
1
1 − 𝑒−2𝑎𝑠
0
2𝑎
𝑒−𝑠𝑡
𝑓(𝑡) 𝑑𝑡 =
1
1 − 𝑒−2𝑎𝑠
0
𝑎
𝑒−𝑠𝑡
𝑓(𝑡) 𝑑𝑡 +
𝑎
2𝑎
−1 𝑒−𝑠𝑡
𝑑𝑡
=
1
1 − 𝑒−2𝑎𝑠
−
1
𝑠
𝑒−𝑠𝑡
0
𝑎
− −
1
𝑠
𝑒−𝑠𝑡
𝑎
2𝑎
=
1 − 𝑒−𝑎𝑠
𝑠(1 + 𝑒−𝑎𝑠)
=
1
𝑠
tanh
𝑎𝑠
2
𝑓 𝑡 = (−1) 𝑡/2

17. Perhatikan fungsi gelombang segitiga g(t) seperti pada gambar berikut.
Jelas bahwa 𝑔′(𝑡) tak lain adalah fungsi gelombang persegi f(t),
sehingga kita dapat memanfaatkan sifat transformasi dari turunan ,
ℒ 𝑔′ 𝑡 = 𝑠𝐺 𝑠 − 𝑔 0
1
𝑠
tanh
𝑎𝑠
2
= 𝑠𝐺 𝑠 − 0
𝐺 𝑠 =
1
𝑠2
tanh
𝑎𝑠
2

18. CONTOH SOAL
Tentukan transformasi Laplace dari fungsi berikut

19. IMPULS
Andaikan gaya 𝑓(𝑡) bekerja hanya untuk selang waktu yang singkat,
misal 𝑎 ≤ 𝑡 ≤ 𝑏 dan 𝑓 𝑡 = 0 di luar selang itu. Contoh khan dari
masalah tersebut adalah : lemparan bola pada tembok, kejut voltase
listrik pada pasien dan lain sebagainya. Dalam situasi itu, pengaruh dari
gaya tersebut lebih tepat diwakili oleh nilai dari integralnya
𝑝 =
𝑎
𝑏
𝑓(𝑡) 𝑑𝑡
dibanding dengan fungsi 𝑓(𝑡) itu sendiri. Nilai 𝑝 dari integral di atas
disebut 𝑖𝑚𝑝𝑢𝑙𝑠 dari gaya 𝑓(𝑡) pada selang waktu [𝑎, 𝑏].

20. Delta Dirac
Suatu gaya dengan impuls 1 bekerja selama waktu 𝜀, gaya tersebut dapat
diformulasikan sebagai
𝑑 𝑎,𝜀 =
1
𝜀
, 𝑗𝑖𝑘𝑎 𝑎 −
𝜀
2
≤ 𝑡 < 𝑎 +
𝜀
2
0, 𝑡 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
Untuk 𝑎 > 0 dan 𝜀 > 0. Jelas bahwa impuls dari 𝑑 𝑎,𝜀(𝑡) adalah 1.
Selanjutnya, delta Dirac diperkenalkan sebagai limit dari 𝑑 𝑎,𝜀(t) atau
𝛿 𝑎(𝑡) ≡ lim
𝜀→0
𝑑 𝑎,𝜀(𝑡)
Jelas bahwa impuls dari 𝛿 𝑎 𝑡 tetap bernilai 1, atau
0
∞
𝛿 𝑎 𝑡 𝑑𝑡 = 1
Dengan demikian fungsi delta Dirac bernilai 0 untuk 𝑡 ≠ 𝑎 dan bernilai +∞ untuk
𝑡 = 𝑎, atau
𝛿 𝑎 𝑡 =
+∞, 𝑗𝑖𝑘𝑎 𝑡 = 𝑎
0, 𝑗𝑖𝑘𝑎 𝑡 ≠ 𝑎

21. PROPOSISI 10. Jika 𝑎 ∈ [0, ∞), maka
0
∞
𝑔 𝑡 𝛿 𝑎 𝑡 𝑑𝑡 = 𝑔(𝑎)
Transformasi Laplace dari delta Dirac langsung dapat diperoleh dengan
menerapkan Proposisi 10, sehingga diperoleh
ℒ 𝛿 𝑎 𝑡 = 𝑒−𝑎𝑠, 𝑢𝑛𝑡𝑢𝑘 𝑎 ≥ 0
Notasi lain bagi fungsi delta Dirac :
𝛿 𝑡 = 𝛿0(𝑡), 𝛿 𝑡 − 𝑎 = 𝛿 𝑎(𝑡)
Jadi, ℒ 𝛿 𝑡 = 1.

22. Implementasi
Sebuah system pegas-massa yang terdiri dari pegas 𝑘 = 4 dan massa 𝑚 = 1. Saat awal,
massa dilepaskan dari posisi 𝑥 0 = 3 dan mulai bergerak. Saat 𝑡 = 2𝜋 massa dipukul palu
dengan impuls 𝑝 = 8. Gerakan massa pada sistem tersebut diberikan oleh solusi masalah
nilai awal
𝑥′′
+ 4𝑥 = 8𝛿2𝜋 𝑡 , 𝑥 0 = 3, 𝑥′
0 = 0
Transformasi Laplace dari masalah nilai awal tersebut menghasilkan
𝑠2
𝑋 𝑠 − 3𝑠 + 4𝑋 𝑠 = 8𝑒−2𝜋𝑠
𝑋 𝑠 =
3𝑠
𝑠2 + 4
+
8𝑒−2𝜋𝑠
𝑠2 + 4
Penerapan invers transformasi Laplace menghasilkan
𝑥 𝑡 = 3 cos 2𝑡 + 4𝑢 𝑡 − 2𝜋 sin 2(𝑡 − 2𝜋)
atau
𝑥 𝑡 =
3 cos 2𝑡 𝑢𝑛𝑡𝑢𝑘 0 ≤ 𝑡 < 2𝜋
3 cos 2𝑡 + 4 sin 2𝑡 , 𝑢𝑛𝑡𝑢𝑘 𝑡 ≥ 2

23. Latihan Soal
1. Buktikan bahwa solusi dari kedua masalah nilai awal berikut adalah
sama
a. 𝑚𝑥′′
+ 𝑘𝑥 = 0, 𝑥(0) = 0, 𝑥′(0) = 𝑣0
b. 𝑚𝑥′′
+ 𝑘𝑥 = 𝑚𝑣0 𝛿 𝑡 , 𝑥 0 = 0, 𝑥′
0 = 0
2. Tentukan solusi masalah nilai awal berikur dan amati gerakan massa
setelah waktu cukup lama
a. 𝑥′′ + 4𝑥 = 𝛿 𝑡 + 𝛿 𝑡 − 𝜋 , 𝑥 0 = 𝑥′ 0 = 0
b. 𝑥′′ + 9𝑥 = 𝛿 𝑡 − 3𝜋 + cos 3𝑡 , 𝑥 0 = 𝑥′ 0 = 0
c. 𝑥′′ + 2𝑥′ + 𝑥 = 𝑡 + 𝛿 𝑡 , 𝑥 0 = 0, 𝑥′ 0 = 1