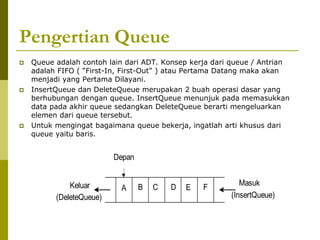
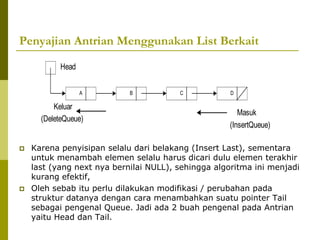
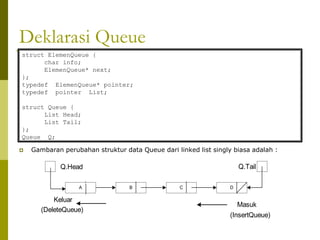
Dokumen tersebut membahas tentang konsep antrian (queue) dan implementasinya menggunakan array dan linked list. Terdapat penjelasan mengenai operasi insert queue dan delete queue serta ilustrasinya. Juga dibahas mengenai queue circular untuk menghindari ketidakefisienan saat delete. Di akhir ada latihan untuk membuat prosedur insert pada priority queue.

1. Queue / Antrian
Akmal, S.Si, MT
Mata Kuliah : Struktur Data

2. Tujuan
 Mahasiswa dapat: menganalisis antrian
dan menyajikannya dengan operasi
InsertQueue dan DeleteQueue, baik
dengan array maupun dengan list berkait
dengan benar

3. Pokok Bahasan
 Pengertian Antrian
 Penyajian Antrian dengan Array dan List
 Operasi Insert Queue dan Delete Queue
 Antrian berprioritas

4. Pengertian Queue
 Queue adalah contoh lain dari ADT. Konsep kerja dari queue / Antrian
adalah FIFO ( “First-In, First-Out” ) atau Pertama Datang maka akan
menjadi yang Pertama Dilayani.
 InsertQueue dan DeleteQueue merupakan 2 buah operasi dasar yang
berhubungan dengan queue. InsertQueue menunjuk pada memasukkan
data pada akhir queue sedangkan DeleteQueue berarti mengeluarkan
elemen dari queue tersebut.
 Untuk mengingat bagaimana queue bekerja, ingatlah arti khusus dari
queue yaitu baris.
A B C D E FKeluar Masuk
Depan
(InsertQueue)(DeleteQueue)

5. Penyajian Antrian Menggunakan List Berkait
 Karena penyisipan selalu dari belakang (Insert Last), sementara
untuk menambah elemen selalu harus dicari dulu elemen terakhir
last (yang next nya bernilai NULL), sehingga algoritma ini menjadi
kurang efektif,
 Oleh sebab itu perlu dilakukan modifikasi / perubahan pada
struktur datanya dengan cara menambahkan suatu pointer Tail
sebagai pengenal Queue. Jadi ada 2 buah pengenal pada Antrian
yaitu Head dan Tail.
B C D
Head
A
Masuk
(InsertQueue)
Keluar
(DeleteQueue)

6. Deklarasi Queue
 Gambaran perubahan struktur data Queue dari linked list singly biasa adalah :
struct ElemenQueue {
char info;
ElemenQueue* next;
};
typedef ElemenQueue* pointer;
typedef pointer List;
struct Queue {
List Head;
List Tail;
};
Queue Q;
B C D
Q.Head
A
Masuk
(InsertQueue)
Keluar
(DeleteQueue)
Q.Tail

7. Insert Queue
Ada 2 kasus yang harus ditangani yaitu :
* Kasus Kosong
 Kasus ada isi
 Dalam hal ini tidak diperlukan lagi pencarian elemen terakhir karena elemen terakhir
selalu dicatat oleh Q.Tail
Q.Head Q.Tail
A
pBaru
Q.Head Q.Tail
A
pBaru
1 2
1. Q.Head=pBaru
2. Q.Tail=pBaru
B C
D
Q.Head
A
pBaru
Q.Tail
1
2
1. Q.Tail->next = pBaru
2. Q.Tail=pBaru

8. Fungsi insertQueue
void insertQueue( Queue& Q, pointer pBaru){
if (Q.Head==NULL && Q.Tail==NULL) { // kosong
Q.Head = PBaru;
Q.Tail = PBaru;
}
else { // ada isi
Q.Tail->next = PBaru;
Q.Tail = PBaru;
}
}

9. Delete Queue
Ada 3 kasus yang harus ditangani yaitu :
a. Queue kosong
Ciri dari Queue kosong adalah Q.Head==NULL dan Q.Tail==NULL
Tidak ada elemen yang dihapus
b. Queue dengan isi 1 elemen
List akan menjadi kosong dengan keadaan Head dan Tail bernilai NULL
Q.Head=NULL
Q.Tail = NULL
c. Queue dengan isi lebih dari 1 elemen
A B C
Q.Head
pHapus
1
3
2
Q.Tail
D

10. Fungsi DeleteQueue
void deleteQueue(Queue& Q, pointer& pHapus){
cout<<"Delete Queue"<<endl;
if (Q.Head==NULL && Q.Tail==NULL) { //kasus kosong
pHapus=NULL;
cout<<"List Queue kosong "<<endl;
}
else if (Q.Head->next==NULL) { // kasus isi 1 elemen
pHapus=Q.Head;
Q.Head=NULL;
Q.Tail=NULL;
}
else { // kasus > 1 elemen
pHapus=Q.Head;
Q.Head=Q.Head->next;
pHapus->next=NULL;
}
}

11. Penyajian Antrian Menggunakan Array
 Deklarasi array untuk mendefinisikan struktur data antrian adalah dengan
cara seperti berikut
 Ada 2 operasi dasar yang bisa dilakukan dengan menggunakan array yaitu
insertQueue dan deleteQueue.
 Untuk membuat sebuah Queue kosong adalah dengan membuat suatu
fungsi createQueue dengan memberikan indeks head=0 dan tail=-1;
const int maxElemen = 255;
struct Queue{
char isi[maxElemen];
int head; // depan
int tail; // belakang
};
void createQueue (Queue& Q){
Q.head = 0;
Q.tail = -1;
}

12. Illustrasi Antrian
 Penyisipan selalu di belakang dengan indexnya bertambah 1 dari keadaan
sebelumnya.
 Sedangkan penghapusan selalu di posisi depan. Selanjutnya semua elemen yang
tersisa digeser posisinya ke depan.
0
1
2
3
4
5
head=0
tail =-1
B
C
D
0
1
2
3
4
5
head=0
tail=3
0
1
2
3
4
5
tail=2
E
0
1
2
3
4
5
tail=3
A
B
C
D
D masuk
A keluar
Langsung di geser
E masuk
Antrian dengan menggeser elemen
C
D
B

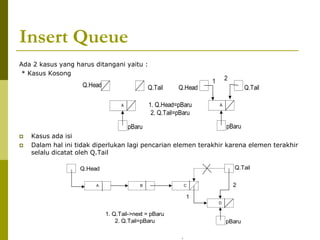
13. Insert Queue / Penyisipan
 Kasus yang ditangani dalam insert Queue adalah jika kapasitas array
sudah penuh dan jika belum. Jika sudah penuh maka tidak bisa lagi
dilakukan penyisipan, tetapi jika belum maka index dari Tail bertambah 1
dan kemudian di posisi index yang baru elemen yang baru disisipkan.
 Fungsi untuk insert Queue adalah sbb:
void insertQueue(Queue& Q, char elemen) {
cout<<"Insert Queue (Antrian) "<<endl;
if (Q.tail==maxElemen-1){
cout<<"Antrian sudah penuh"<<endl;
}
else {
Q.tail=Q.tail + 1;
Q.isi[Q.tail] = elemen;
}
}

14. Delete Queue / Penghapusan
 Untuk melakukan proses delete Queue dengan cara sbb:
 Kasus yang ditangani ádalah kasus kosong dan ada isi. Untuk kasus kosong (dengan
ciri index head>tail, atau tail=-1) maka tidak ada yang dihapus, sementara untuk
kasus ada isi setelah data yang dihapus diamankan maka selanjutnya elemen yang
lain digeser ke depan satu persatu.
void deleteQueue(Queue& Q, char& elemenHapus){
cout<<"Delete Queue (Antrian) "<<endl;
if (Q.head>Q.tail){ // atau Q.tail=-1
cout<<"Antrian kosong"<<endl;
}
else {
elemenHapus= Q.isi[Q.head]; //Q.head=0
for (int i=0;i<Q.tail;i++){ // Geser ke depan
Q.isi[i]=Q.isi[i+1];
}
Q.tail=Q.tail-1;
}
}

15. Queue Circular
 Terlihat dalam fungsi sebelumnya ada ketidakefisienan ketika dilakukan proses
delete yaitu selalu terjadi proses pergeseran elemen. Untuk itu dilakukan pengaturan
penyimpanan array dengan bentuk circular (memutar) untuk menghindari ketidak
efisienan ketika proses delete tersebut. Dengan bentuk memutar ini maka elemen
pertama larik terletak berdekatan dengan elemen terakhir larik.
 Gambaran logic
D
E
F
0
1
2
3
4
5
Depan=3
Belakang=5
D
E
F
0
1
2
3
4
5
Depan=3
Belakang=0
F
0
1
2
3
4
5 Depan=5
Belakang=0
F
0
1
2
3
4
5 Depan=5
Belakang=3
G
G G
H
I
G masuk
D keluar
E keluar
H masuk
I masuk
Antrian secara circular (memutar)

16. Insert Queue Circular
 Kasus yang ditangani adalah kasus queue masih kosong dan kasus sudah ada isi.
Jika kosong maka indeks Q.Head=0 dan juga Q.Tail=0.
 Jika ada isi maka dilihat posisi Q.Tail nya. Jika posisi Q.Tail belum di akhir indeks
maka posisi indeks Q.tail akan bertambah 1, tetapi jika sudah di akhir indeks maka
penyisipan akan diletakkan diposisi 0.
if (Q.tail< maxElemen-1 ) {
Q.tail=Q.tail+1;
}
else {
Q.tail=0;
}
 Selanjutnya akan diperiksa apakah posisi baru yang akan ditempati masih kosong
atau sudah ada isi. Jika ada isi artinya antrian sudah penuh.
void createQueue(Queue& Q){
Q.head = -1;
Q.tail = -1;
}

17. Fungsi InsertQueue sirkular
void insertQueue(Queue& Q, char elemen) {
int posisiTemp;
cout<<"Insert Queue (Antrian) "<<endl;
if (Q.tail==-1) { // kosong pertama kali
Q.head=0;
Q.tail=0;
Q.isi[Q.tail] = elemen;
}
else {
posisiTemp=Q.tail; // amankan posisi Q.tail
if (Q.tail< maxElemen-1 ) { // proses circular
Q.tail=Q.tail+1;
}
else { // Q.tail>=maxElemen-1
Q.tail=0;
}
if (Q.tail==Q.head){
cout<<"Antrian sudah penuh"<<endl;
Q.tail=posisiTemp; // kembalikan posisi Q.tail
}
else {
Q.isi[Q.tail] = elemen;
}
}
}

18. Delete Queue Circular
void deleteQueue(Queue& Q, char& elemenHapus){
cout<<"Delete Queue (Antrian) "<<endl;
if (Q.head==-1 ) { //kosong
cout<<"Antrian kosong"<<endl;
}
else if (Q.head==Q.tail){ // isi 1 elemen
elemenHapus= Q.isi[Q.head];
Q.isi[Q.head]=' ';
Q.head=-1; // kembalikan ke kosong
Q.tail=-1;
}
else { // isi > 1 elemen
elemenHapus= Q.isi[Q.head];
Q.isi[Q.head]=' ';
if (Q.head<maxElemen-1) {
Q.head=Q.head+1;
}
else { // Q.head=maxElemen-1
Q.head=0;
}
}
}

19. Latihan dan Tugas
 Buatlah prosedur untuk menyisipkan elemen dalam Priority Queue / Antrian
berprioritas yang bisa terjadi diawal, ditengah atau dibelakang antrian. Priority
Queue banyak digunakan dalam S.O. misalnya untuk mencetak suatu job duluan
karena punya prioritas tinggi.
Struktur datanya adalah sbb :
type ElmtQueue : <Info : InfoType,
Prior : integer,
Next : address >
type Queue : < Head : address, Tail : address>
Procedure InsertPriorQueue (Input / Output Q : Queue, input P : address)
{I.S. Queue mungkin kosong }
{F.S. Priority Queue adalah penyisipan elemen P ke dalam antrian dengan aturan khusus
sbb :
 Elemen P dengan prioritas tertentu (10 - tertinggi, 1 - terendah) akan menyisip
sebelum elemen dengan prioritas yang lebih rendah darinya.
 Jika prioritas sama maka P akan menyisip tepat dibelakang deretan elemen yang
sama prioritasnya
 P akan menyisip dibelakang antrian jika prioritasnya paling kecil atau sama dengan
prioritas Tail