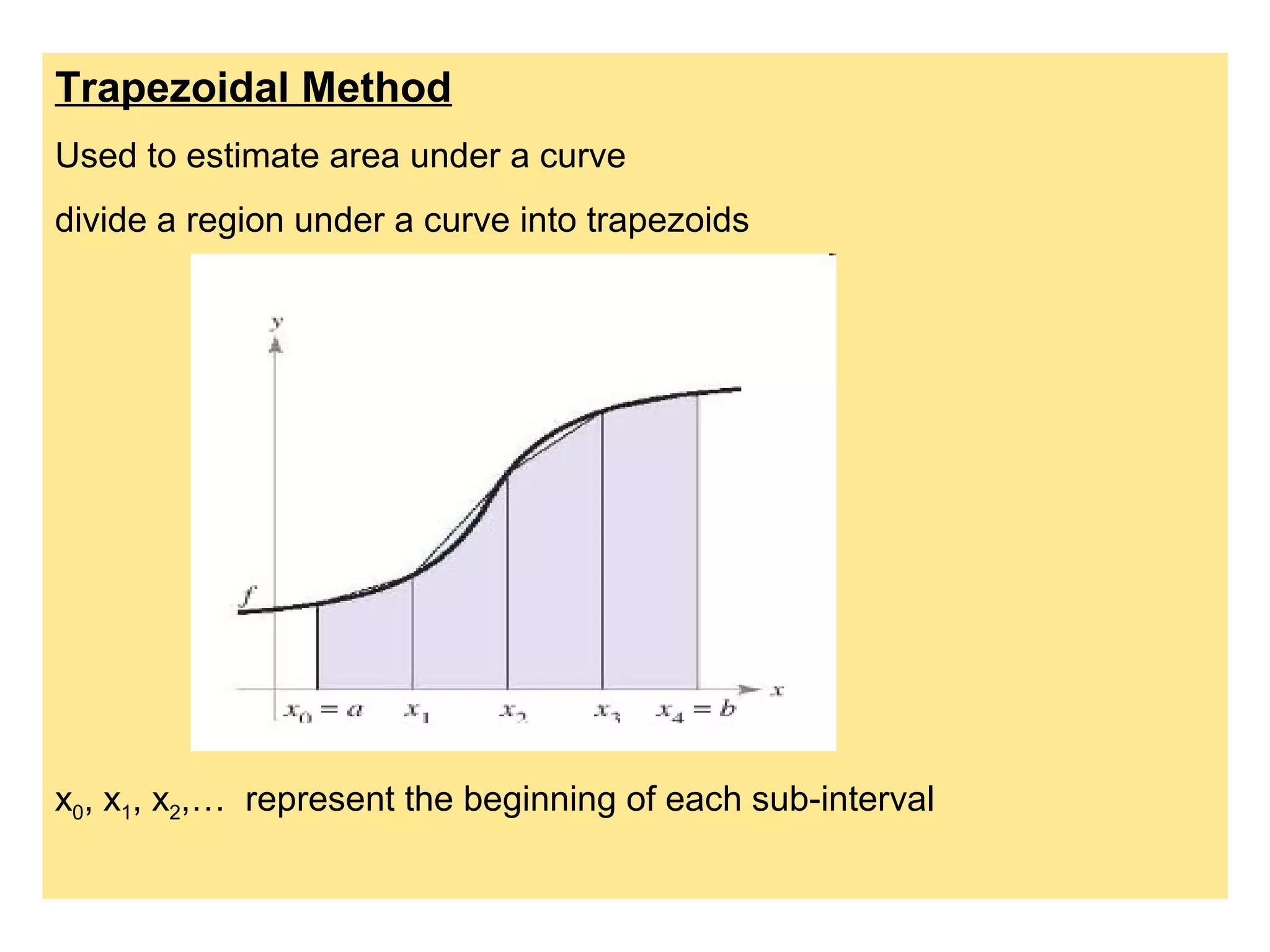
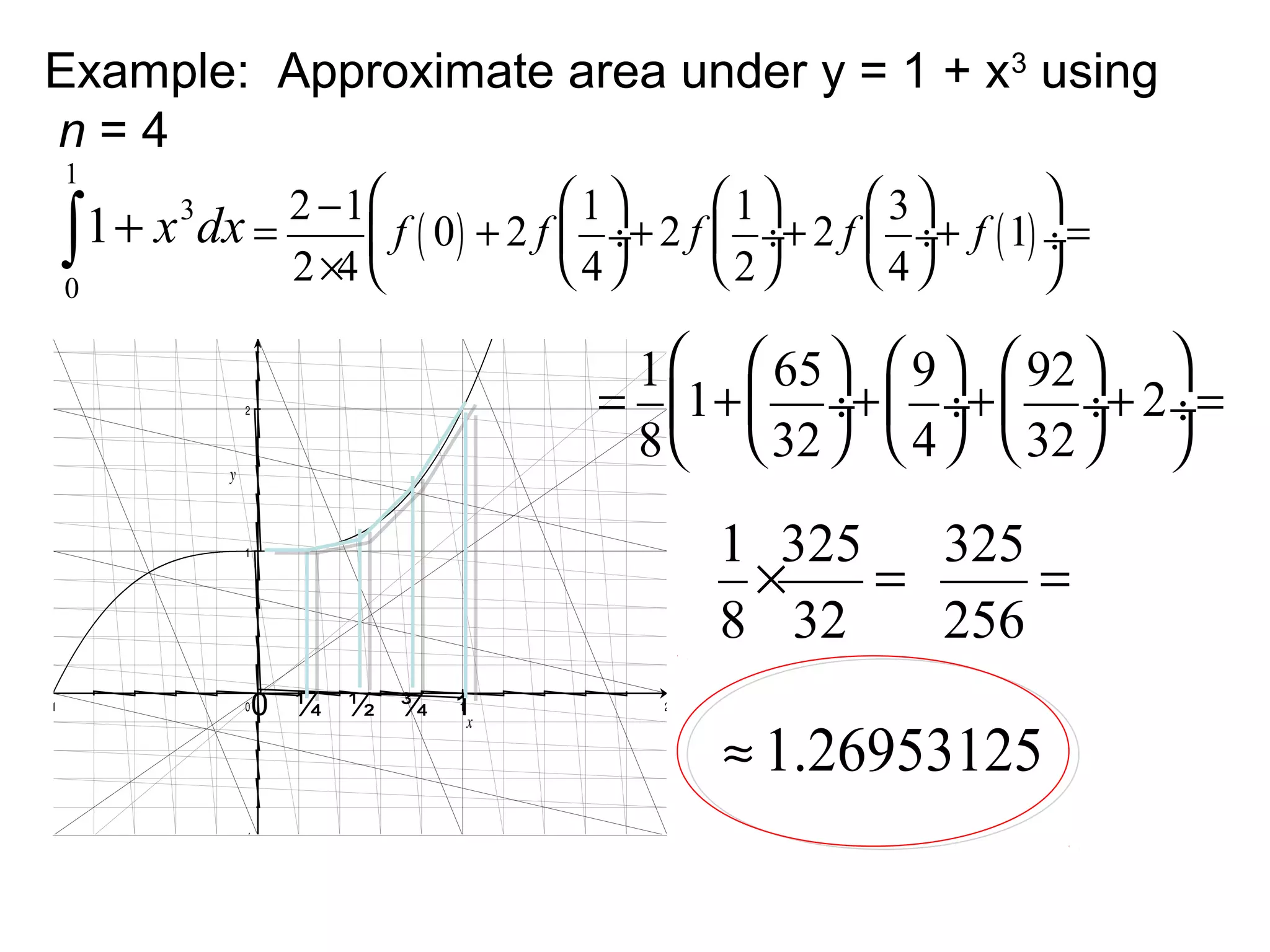
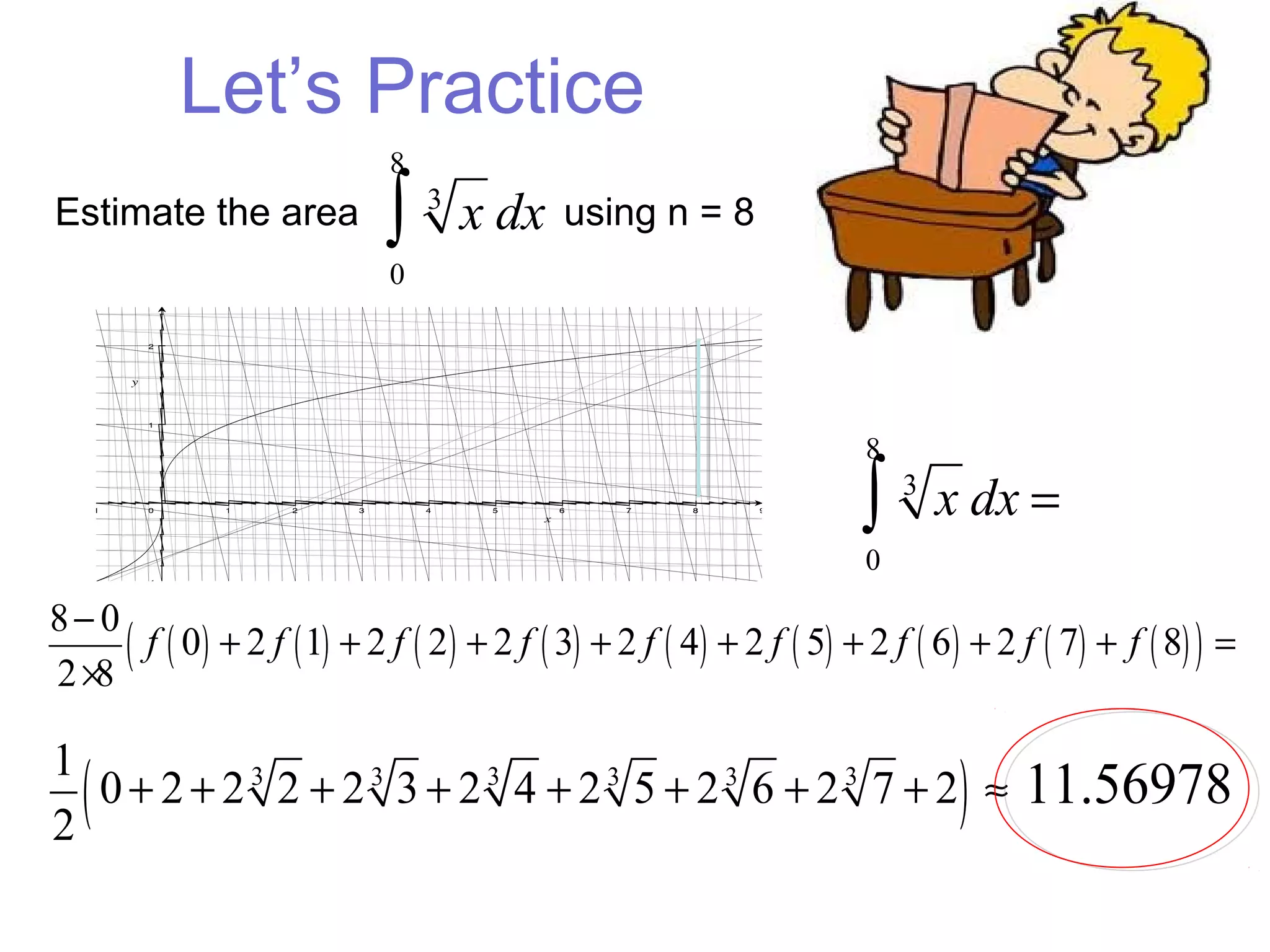
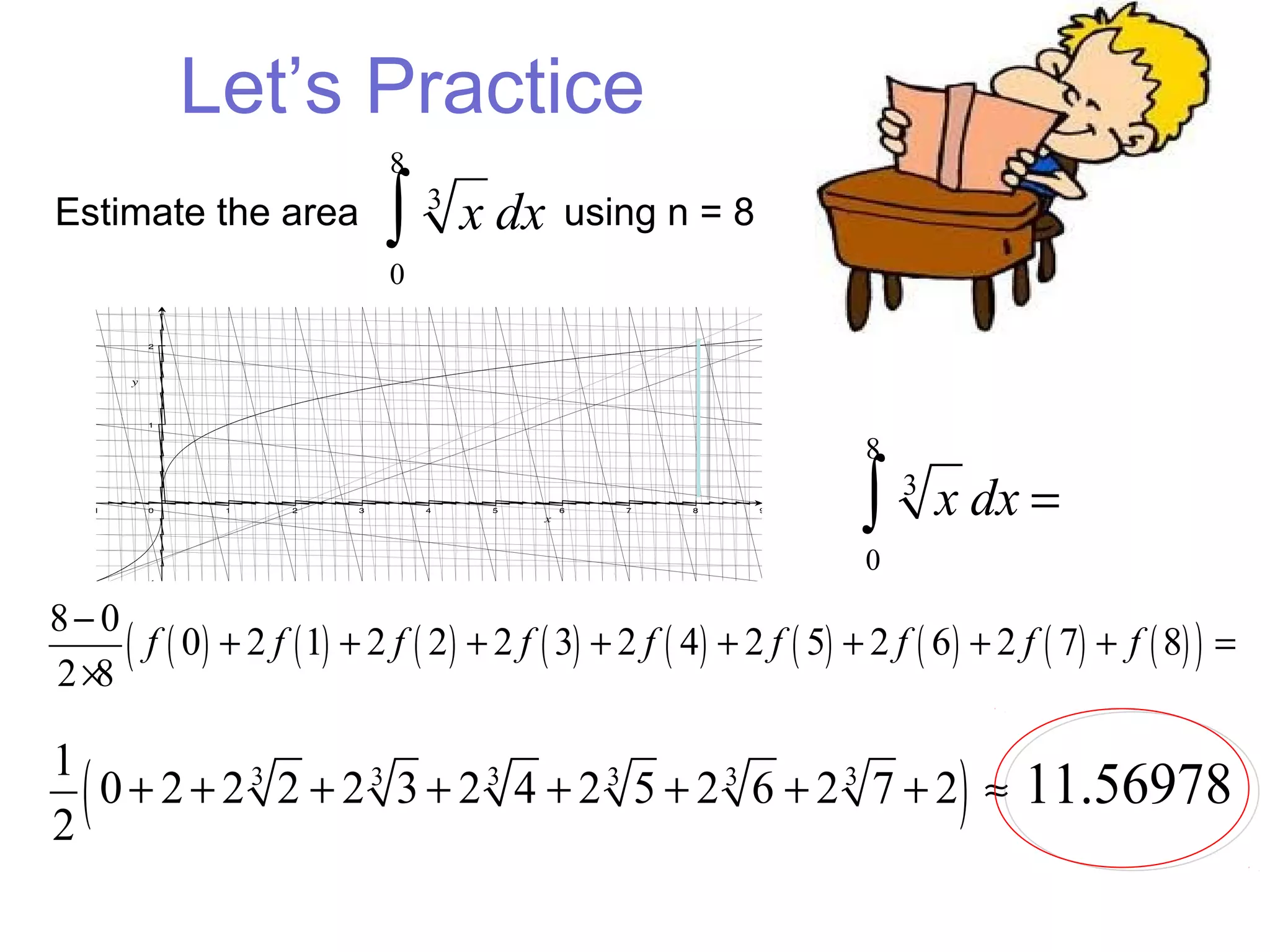
The trapezoidal rule is used to approximate the area under a curve by dividing it into trapezoids. It takes the average of the function values at the beginning and end of each sub-interval multiplied by the sub-interval width. The general formula sums these values over all sub-intervals divided by the number of intervals. An example calculates the area under y=1+x^3 from 0 to 1 using n=4 sub-intervals and gets an approximate value of 1.26953125.

1. Numerical Integration
Trapezoidal Approximation

2. Trapezoidal Method
Used to estimate area under a curve
divide a region under a curve into trapezoids
x0, x1, x2,… represent the beginning of each sub-interval

3. Trapezoidal Rule
b
∫
a
b−a
( f ( x0 ) + 2 f ( x1 ) + 2 f ( x2 ) +  + f ( xn ) )
f ( x ) dx =
2n
Where n is the number of sub-intervals between a and b
Parts:
b−a
2n
x0 , x1 , , xn
→ calculate from given intervals
→ the starting x-value of each sub-interval
1, 2, 2, 2,…, 1 → coefficients in trapezoidal rule

4. Example: Approximate area under y = 1 + x3 using
n=4
1

1
1
 3
2 −1 
1 + x dx =
 f ( 0) + 2 f  ÷+ 2 f  ÷+ 2 f  ÷+ f ( 1) ÷=
4
2
4
2 ×4 

0
∫
3
1   65   9   92  
= 1+  ÷+  ÷+  ÷+ 2 ÷=
8   32   4   32  
1 325 325
×
=
=
8 32
256
0 ¼ ½ ¾ 1
≈ 1.26953125

5. Let’s Practice
8
Estimate the area
∫
3
x dx
using n = 8
0
8
∫
3
x dx =
0
8− 0
( f ( 0) + 2 f ( 1) + 2 f ( 2) + 2 f ( 3) + 2 f ( 4) + 2 f ( 5) + 2 f ( 6) + 2 f ( 7) + f ( 8) ) =
2 ×8
(
)
1
0+ 2+23 2 + 23 3+ 23 4 +23 5 +23 6 +23 7 +2 ≈
2
11.56978

6. Let’s Practice
8
Estimate the area
∫
3
x dx
using n = 8
0
8
∫
3
x dx =
0
8− 0
( f ( 0) + 2 f ( 1) + 2 f ( 2) + 2 f ( 3) + 2 f ( 4) + 2 f ( 5) + 2 f ( 6) + 2 f ( 7) + f ( 8) ) =
2 ×8
(
)
1
0+ 2+23 2 + 23 3+ 23 4 +23 5 +23 6 +23 7 +2 ≈
2
11.56978