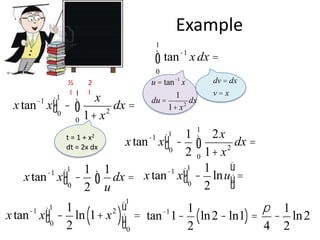
Integration by parts is a technique for evaluating integrals of the form ∫udv, where u and v are differentiable functions. It works by expressing the integral as uv - ∫vdu. Some examples of integrals solved using integration by parts include ∫xe^xdx, ∫lnxdx, and ∫xe^-xdx. The technique can also be used repeatedly and for definite integrals between limits a and b using the formula ∫abudv = uv|_a^b - ∫avdu.

1. Integration by Parts

2. Integration by parts is used when integrating the
product of two expressions . We can also sometimes
use integration by parts when we want to integrate a
function that cannot be split into the product of two
things.
udv = uv - ò v du
ò

3. Let’s see some examples
ò x cos x dx =
u=x
du = dx
dv = cos x dx
Sdv = Scos x dx
v = sin x
xsin x - ò sin x dx = xsin x - (-cos x ) + C

4. More Examples
ò xe
x
dx =
u=x
du = dx
xe - ò e dx =
x
x
xe x - e x + C
dv = ex dx
Sdv = Sex dx
v = ex

5. One More !!!
ò ln x dx =
u = ln x
du = 1/x dx
x ln x - ò dx =
dv = dx
S dv = S dx
v=x
x ln x - x +C

6. Repeated Integration by Parts
òxe
2 -x
u = x2
du = 2x dx
dx = x (-e
2
dv = e-x dx
Sdv =S e-x dx
v = -e-x
-x
) - ò -e (2x) dx =
-x
-x 2 e-x + 2 ò xe- x dx =
é-xe- x - ò -e- x dxù =
-x e + 2 ë
û
2 -x
u=x
du = dx
dv = e-x dx
Sdv =S e-x dx
v = -e-x
-x 2 e-x + 2 (-xe- x - e- x ) + C = -x 2 e-x - 2xe-x - 2e- x + C =
-e- x ( x 2 + 2x + 2) + C

7. Integration by Parts for Definite
Integrals
b
b
udv = uv] a - ò v du
ò
a
b
a

8. Example
1
ò tan
-1
x dx =
0
½
I 1
x tan x ù û0
1
-1
2
I
x
ò 1+ x 2 dx =
0
x2
t=1+
dt = 2x dx
ù -1
x tan xû
0
2
-1
1
ò
u = tan -1 x
1
du =
dx
2
1+ x
dv = dx
v=x
1 1 2x
x tan -1 xù - ò
dx =
û0
2
2 0 1+ x
ù
1
1
-1 ù1
dx = x tan xû0 - lnuú =
û
2
u
1
ù - 1 ln (1+ x 2 )ù = tan-1 1- 1 ( ln 2 - ln1) = p - 1 ln 2
x tan xû
ú
0
û0
2
2
4 2
-1
1
1