The document presents a lecture on numerical integration methods, specifically focusing on the trapezoidal rule, Simpson's 1/3 rule, and Simpson's 3/8 rule. It provides definitions and formulas for each method and includes example calculations for evaluating the integral of 1/(1+x^2) using different step sizes. The calculated results illustrate the application of these integration techniques.

1. ARHAM VEERAYATAN INSTITUTE
OF ENGINEERING, TECHNOLOGY & RESEARCH
NUMERICAL INTEGRATION
1
PRESENTED BY
KOTADIYA URVISH(150920106001)
KATHIRIYA VISHAL(150920106003)
VYAS KEYUR (150920106004)

2. TOPIC
1. Trapezoidal Rule
2. Simson
1
3
Rule
3. Simson
3
8
Rule
9 May 2017
2

3. 9 May 2017
3
1. Trapezoidal Rule

4. DEFINITION & FORMULA
 If 𝑥0, 𝑥1, 𝑥2,…. 𝑥 𝑛 be the value of equally spaced x’s and 𝑦0, 𝑦1, 𝑦2,…. 𝑦𝑛
be the corresponding values of y’s then,
𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
2
[ (𝑦0+𝑦𝑛)+2(𝑦1+𝑦2+𝑦3+….. 𝑦 𝑛−1) ]
 Where h is difference between two consecutive x’s
9 May 2017
4

5. 9 May 2017
5
2. Simson
𝟏
𝟑
Rule

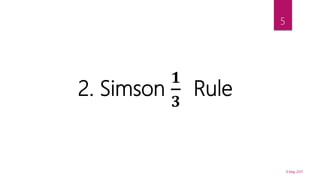
6. DEFINITION & FORMULA
 If 𝑥0, 𝑥1, 𝑥2,…. 𝑥 𝑛 be the value of equally spaced x’s and 𝑦0, 𝑦1,
𝑦2,…. 𝑦𝑛 be the corresponding values of y’s then,
𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
3
[ (𝑦0+𝑦𝑛)+4(𝑦1+𝑦3+…..+ 𝑦 𝑛−1)+2(𝑦2+𝑦4+…..+𝑦 𝑛−2)]
 Where h is difference between two consecutive x’s
9 May 2017
6

7. 9 May 2017
7
3. Simson
𝟑
𝟖
Rule

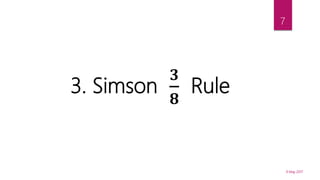
8. DEFINITION & FORMULA
 If 𝑥0, 𝑥1, 𝑥2,…. 𝑥 𝑛 be the value of equally spaced x’s and 𝑦0, 𝑦1, 𝑦2,…. 𝑦𝑛 be
the corresponding values of y’s then,
𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
3ℎ
8
[𝑦0+3(𝑦1+𝑦2+𝑦4+𝑦5+…..+𝑦 𝑛−1)+2(𝑦3+𝑦6+….. 𝑦 𝑛−3)+𝑦𝑛 ]
 Where h is difference between two consecutive x’s
9 May 2017
8

9. EXAMPLE
 Evaluate 0
1 𝑑𝑥
1+𝑥2 𝑢𝑠𝑖𝑛𝑔
(A) Trapezoidal rule taking h =
1
5
(B) Simson’s
1
3
Rule taking h=
1
4
(C) Simson’s
3
8
Rule taking h=
1
6
9 May 2017
9

10. (A) Trapezoidal rule taking h =
1
5

𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
2
[ (𝑦0+𝑦𝑛)+2(𝑦1+𝑦2+𝑦3+….. 𝑦 𝑛−1) ]
h =
1
5
=0.2
𝑥0 = 0 , 𝑥1 = 0.2 , 𝑥2 = 0.4 , 𝑥3 = 0.6 , 𝑥4 = 0.8 , 𝑥5 = 1
∴ 𝑦0 = f(𝑥0) =
1
1+(0)2 = 1
∴ 𝑦1 = f(𝑥1) =
1
1+(0.2)2 = 0.961
∴ 𝑦2 = f(𝑥2) =
1
1+(0.4)2 = 0.862
∴ 𝑦3 = f(𝑥3) =
1
1+(0.6)2 = 0.7352
∴ 𝑦4 = f(𝑥4) =
1
1+(0.8)2 = 0.6097
∴ 𝑦5 = f(𝑥5) =
1
1+(1)2 = 0.5
9 May 2017
10

11. 9 May 2017
11
𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
2
[ (𝑦0+𝑦𝑛)+2(𝑦1+𝑦2+𝑦3+….. 𝑦 𝑛−1) ]
0
1 1
1+𝑥2 =
0.2
2
[ (1+0.5)+2(0+0.961+0.862+0.7352+0.6097+0.5)]
= 0.1 [ 1.5 +6.3358 ]
0
1 1
1+𝑥2 = 0.78358

12. (B) Simson’s
1
3
Rule taking h=
1
4

𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
3
[ (𝑦0+𝑦 𝑛)+4(𝑦1+𝑦3+…..+ 𝑦 𝑛−1)+2(𝑦2+𝑦4+…..+𝑦 𝑛−2)]
h =
1
4
= 0.25
𝑥0 = 0 , 𝑥1 = 0.25 , 𝑥2 = 0.50 , 𝑥3 = 0.75 , 𝑥4 = 1
∴ 𝑦0 = f(𝑥0) =
1
1+(0)2 = 1
∴ 𝑦1 = f(𝑥1) =
1
1+(0.25)2 = 0.9411
∴ 𝑦2 = f(𝑥2) =
1
1+(0.50)2 = 0.8
∴ 𝑦3 = f(𝑥3) =
1
1+(0.75)2 = 0.64
∴ 𝑦4 = f(𝑥4) =
1
1+(1)2 = 0.5
9 May 2017
12

13. 9 May 2017
13𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
ℎ
3
[ (𝑦0+𝑦 𝑛)+4(𝑦1+𝑦3+…..+ 𝑦 𝑛−1)+2(𝑦2+𝑦4+…..+𝑦 𝑛−2)]
0
1 1
1+𝑥2 dx =
0.25
3
[ (1+0.5)+4(0.9411+0.64)+2(0.8+0.5)]
= 0.0833 [ 1.5 +6.3244+2.6 ]
0
1 1
1+𝑥2dx = 0.8686

14. (C) Simson’s
3
8
Rule taking h=
1
6

𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
3ℎ
8
[𝑦0+3(𝑦1+𝑦2+𝑦4+𝑦5+…..+𝑦 𝑛−1)+2(𝑦3+𝑦6+….. 𝑦 𝑛−3)+𝑦𝑛 ]
h =
1
6
= 0.166
𝑥0 = 0 , 𝑥1 = 0.166 , 𝑥2 = 0.333 , 𝑥3 = 0.499 , 𝑥4 = 0.666 , 𝑥5 = 0.833 , 𝑥6 = 0.999 , 𝑥7 = 0.1.1663
∴ 𝑦0 = f(𝑥0) =
1
1+(0)2 = 1
∴ 𝑦1 = f(𝑥1) =
1
1+(0.166)2 = 0.9731
∴ 𝑦2 = f(𝑥2) =
1
1+(0.333)2 = 0.900
∴ 𝑦3 = f(𝑥3) =
1
1+(0.499)2 = 0.800
∴ 𝑦4 = f(𝑥4) =
1
1+(0.666)2 = 0.6927
∴ 𝑦5 = f(𝑥5) =
1
1+(0.833)2 = 0.59035
∴ 𝑦6 = f(𝑥6) =
1
1+(0.999)2 = 0.5
9 May 2017
14

15. 9 May 2017
15𝑥0
𝑥 𝑛
𝑓(𝑥)dx =
3ℎ
8
[𝑦0+3(𝑦1+𝑦2+𝑦4+𝑦5+…..+𝑦 𝑛−1)+2(𝑦3+𝑦6+….. 𝑦 𝑛−3)+𝑦 𝑛 ]
0
1 1
1+𝑥2 dx =
3(0.166)
3
[ 1+3(0.9731+0.9+0.6927+0.5903)+2(0.8)+0.5]
= 0.06225 [ 1+9.4683+1.6+0.5 ]
0
1 1
1+𝑥2dx = 0.7823

16. Thank
you
16