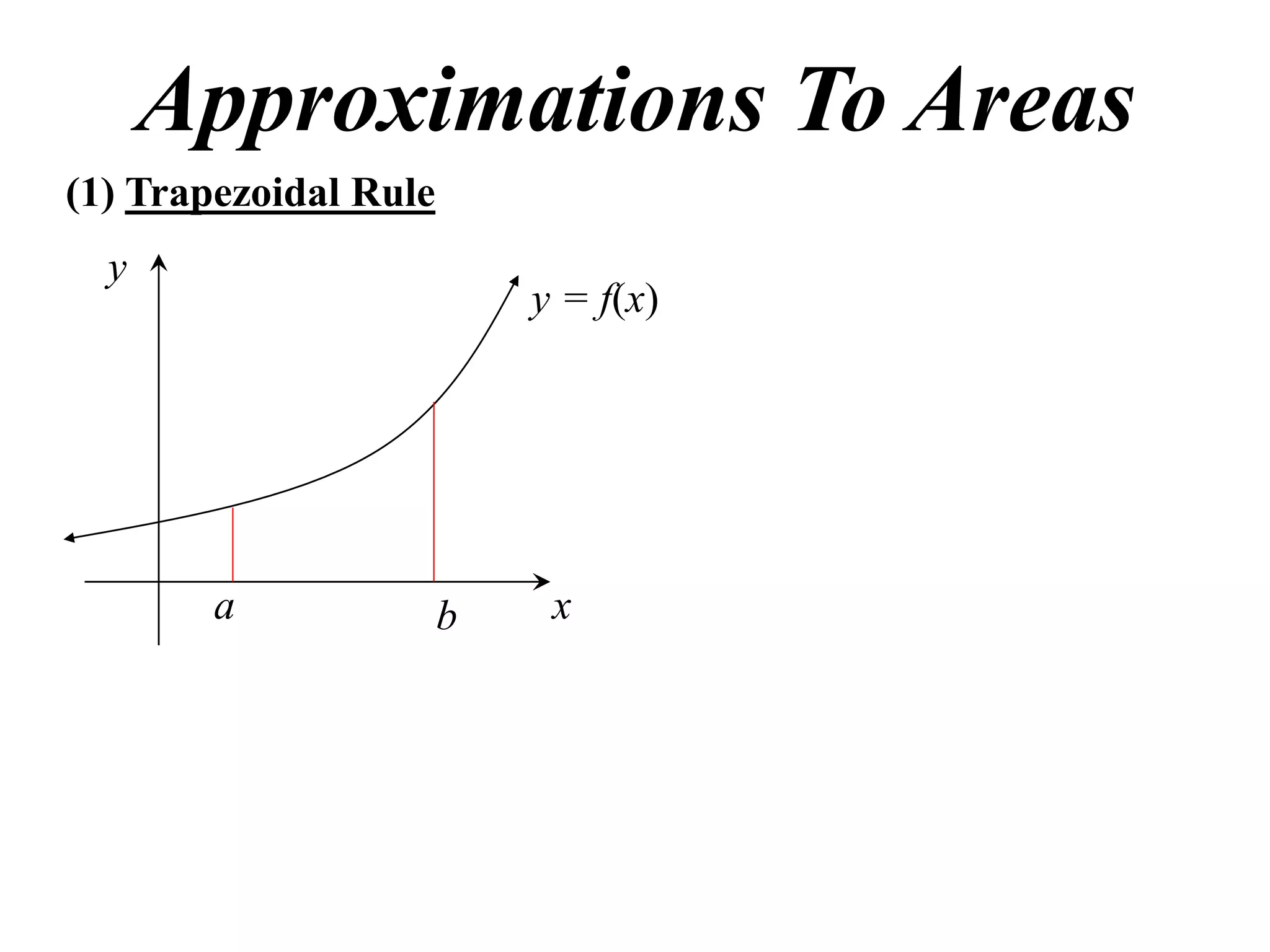
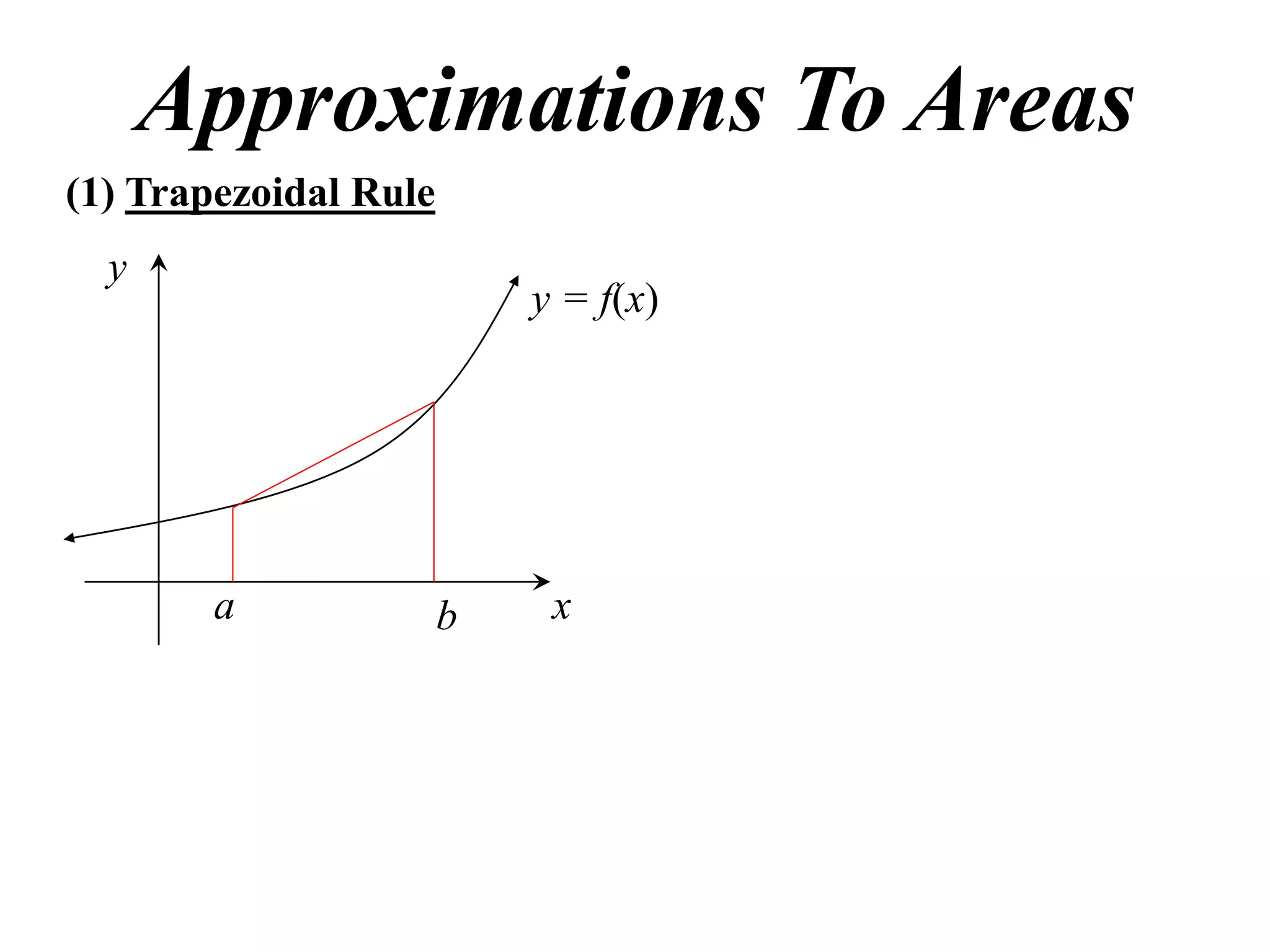
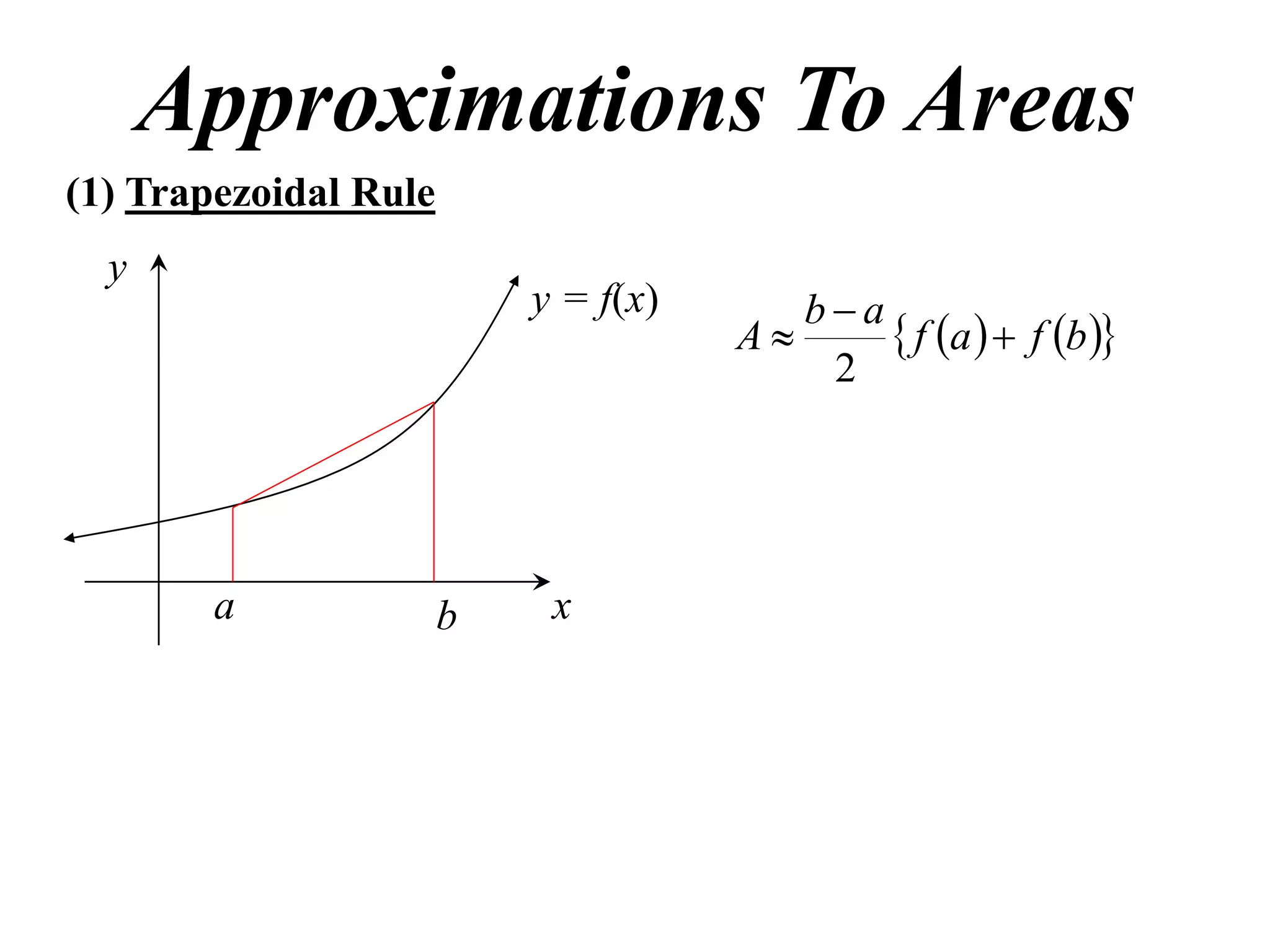
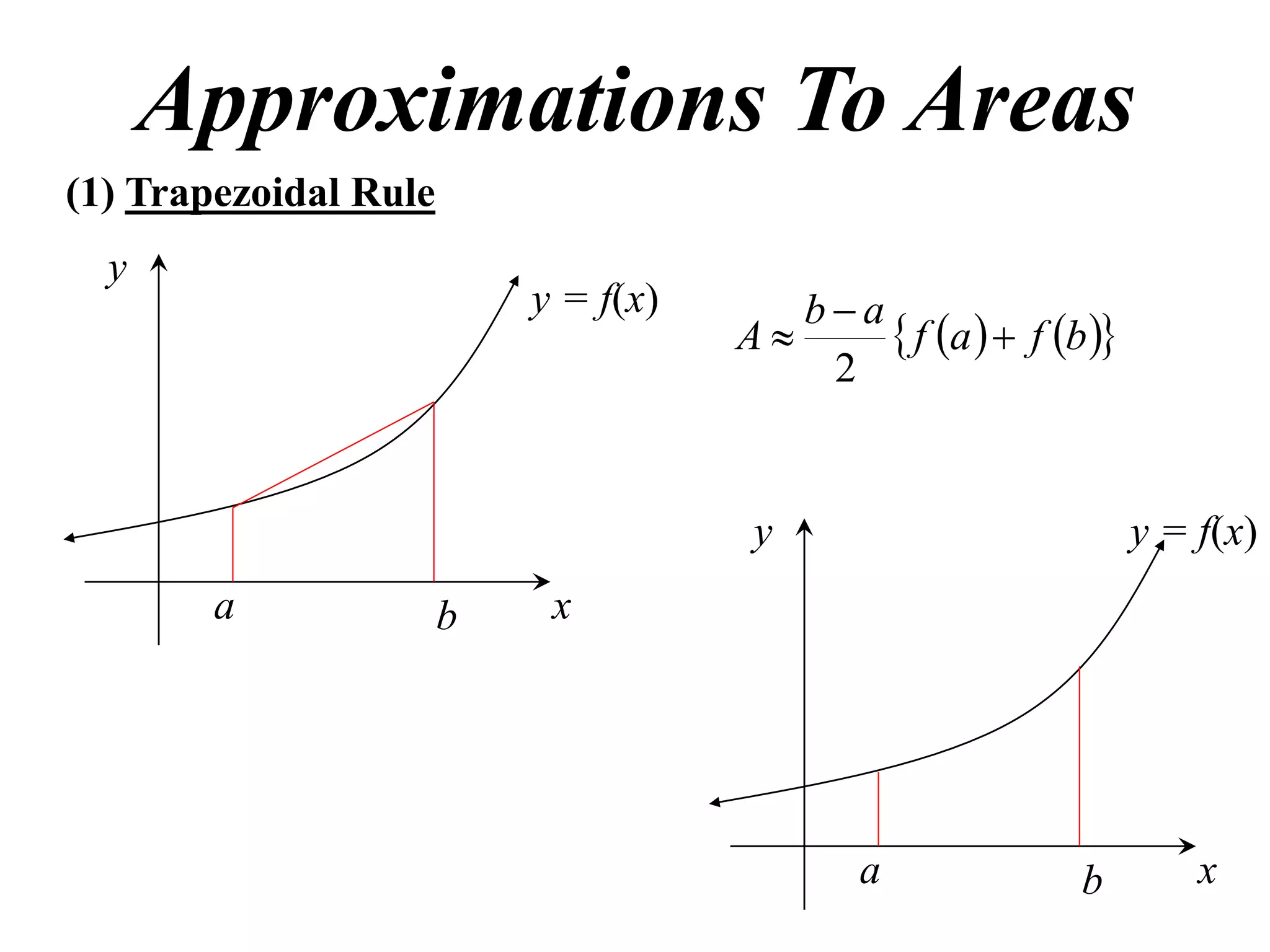
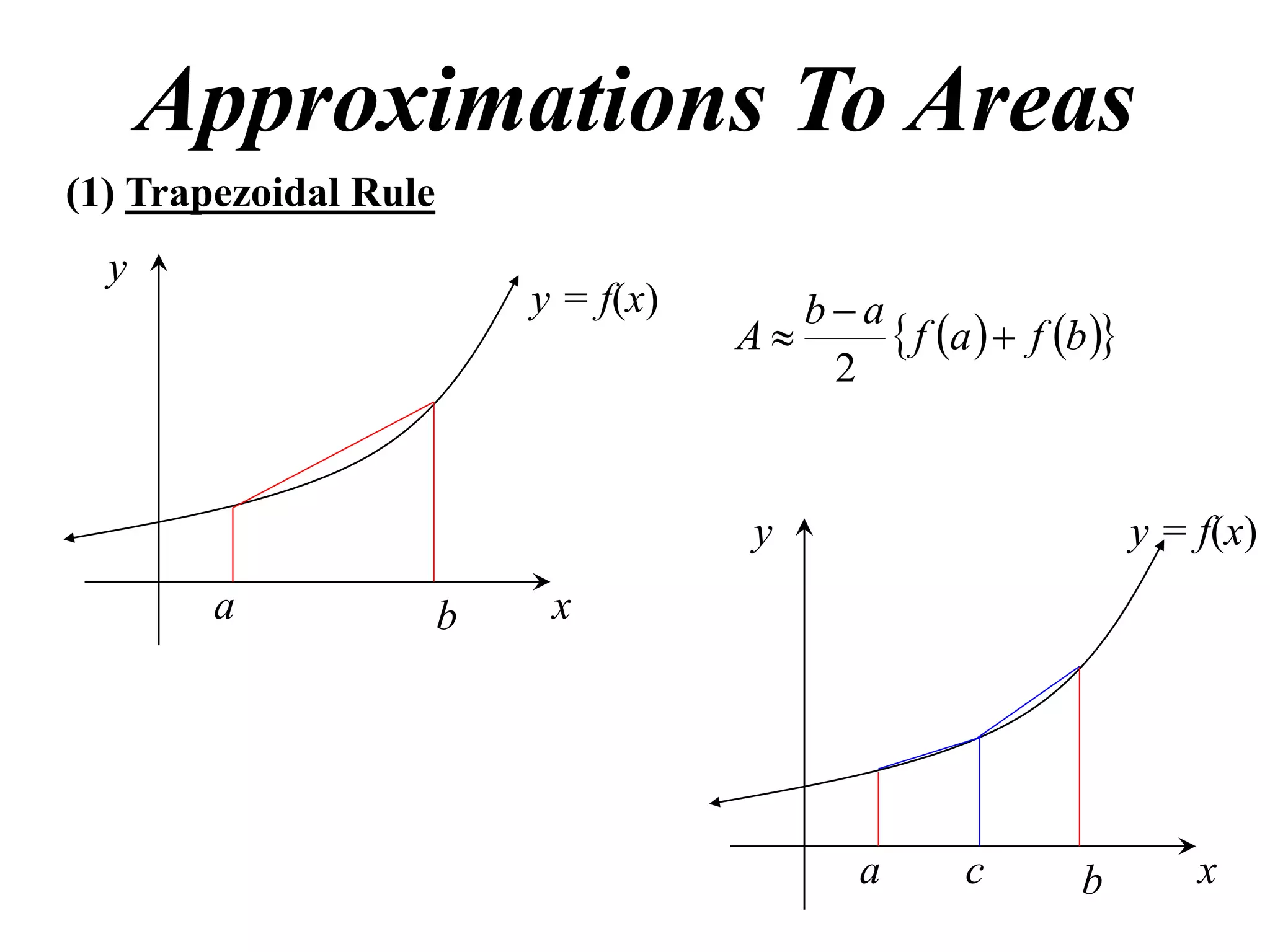
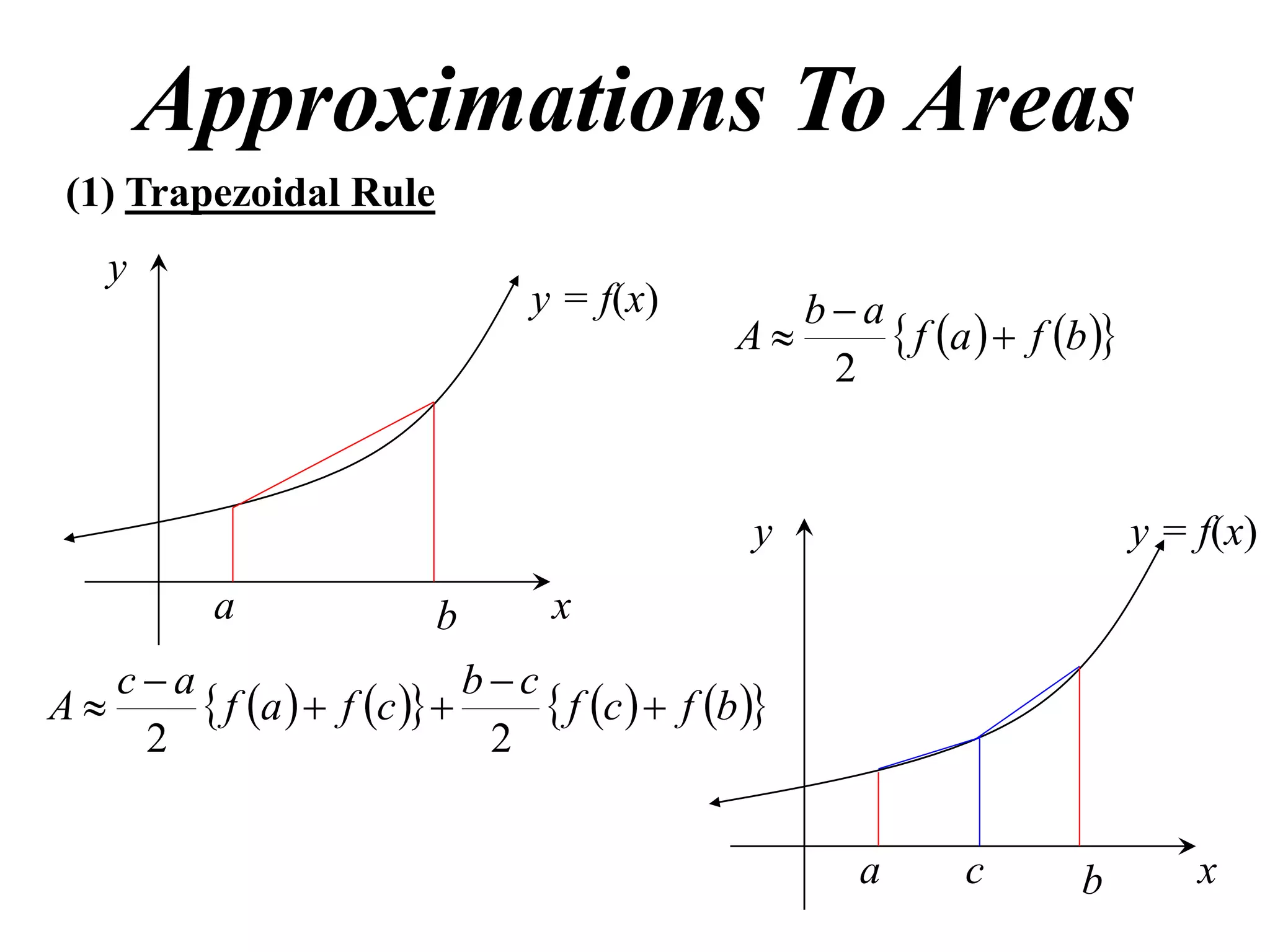
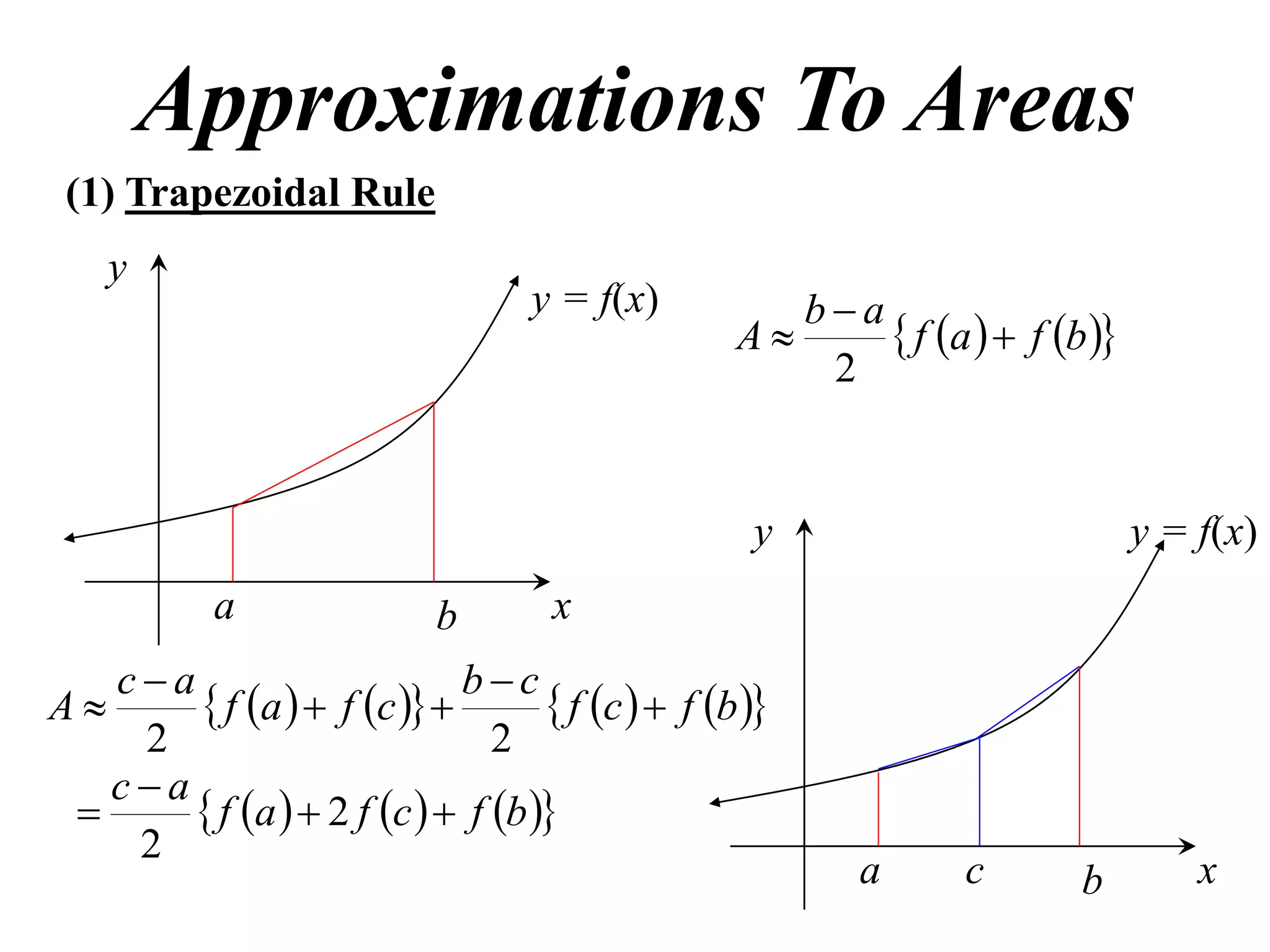
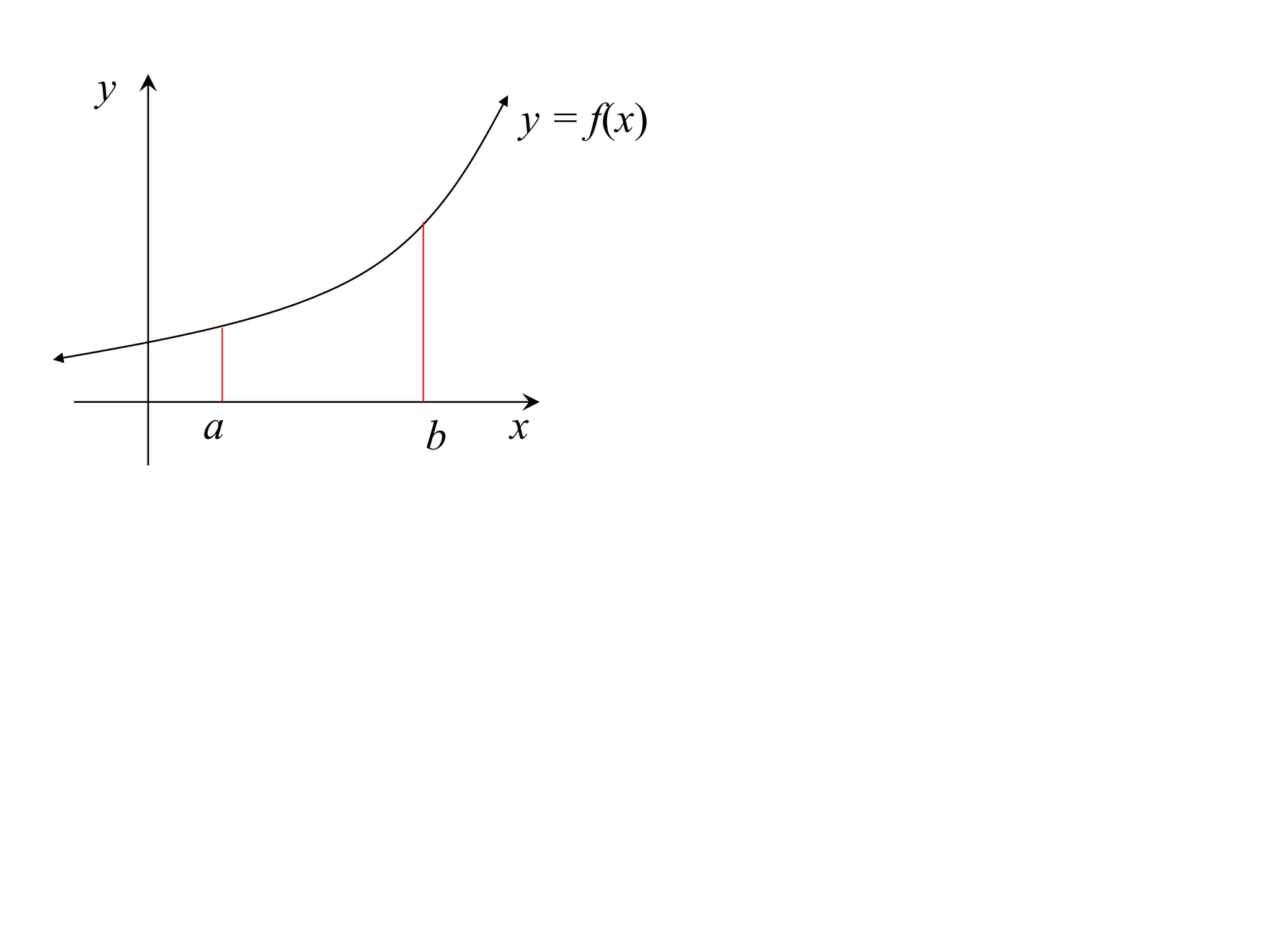
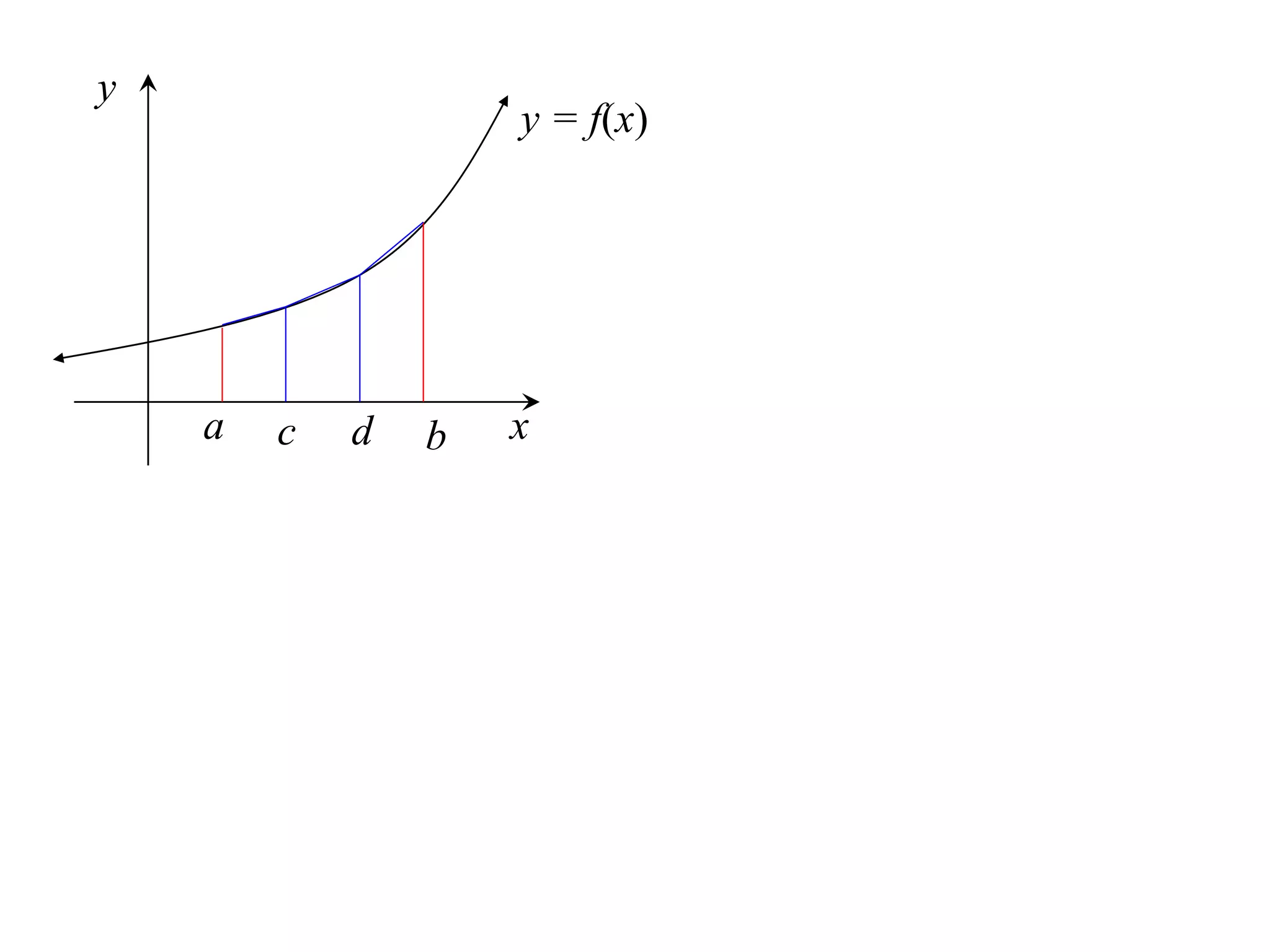
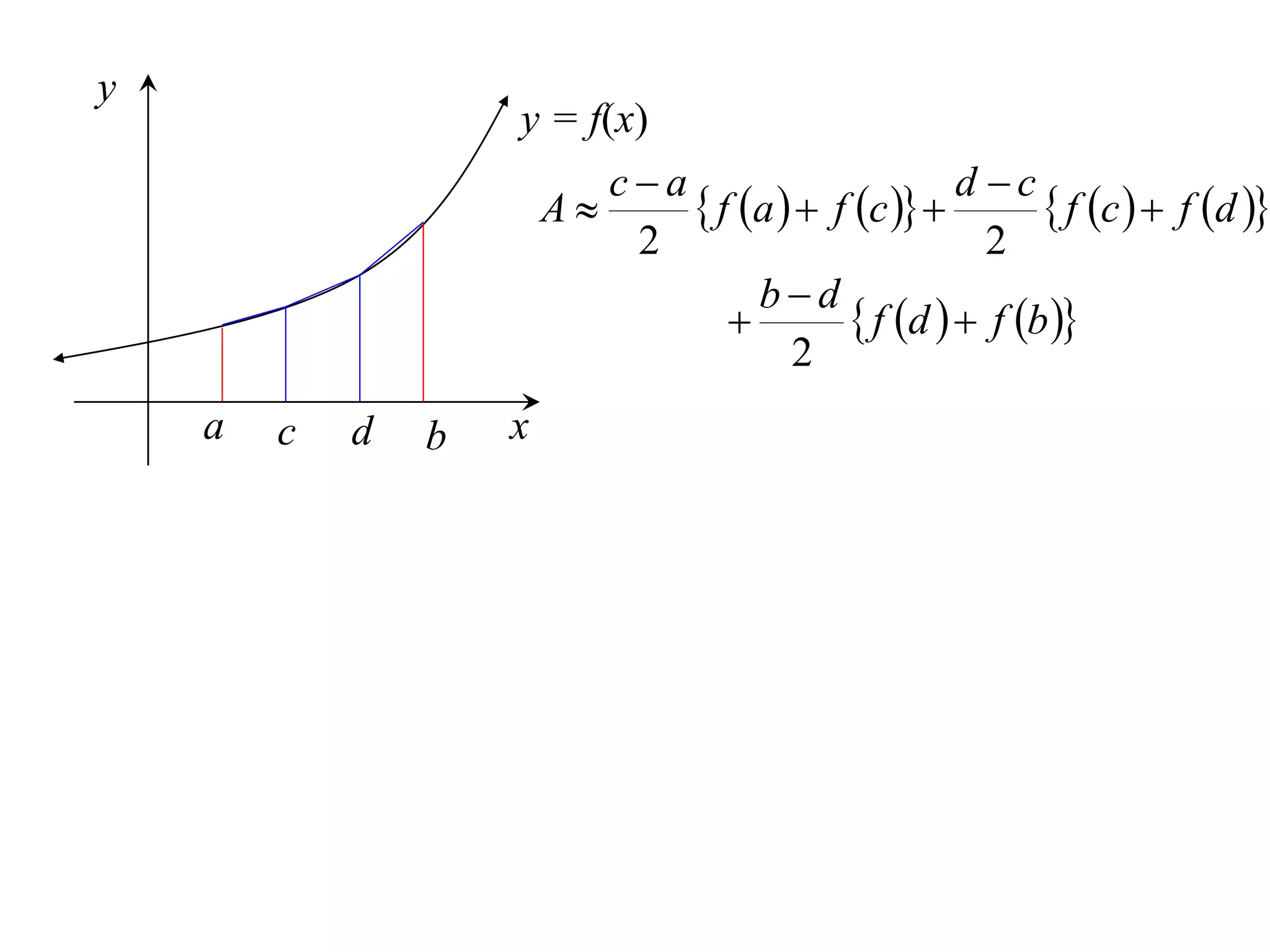
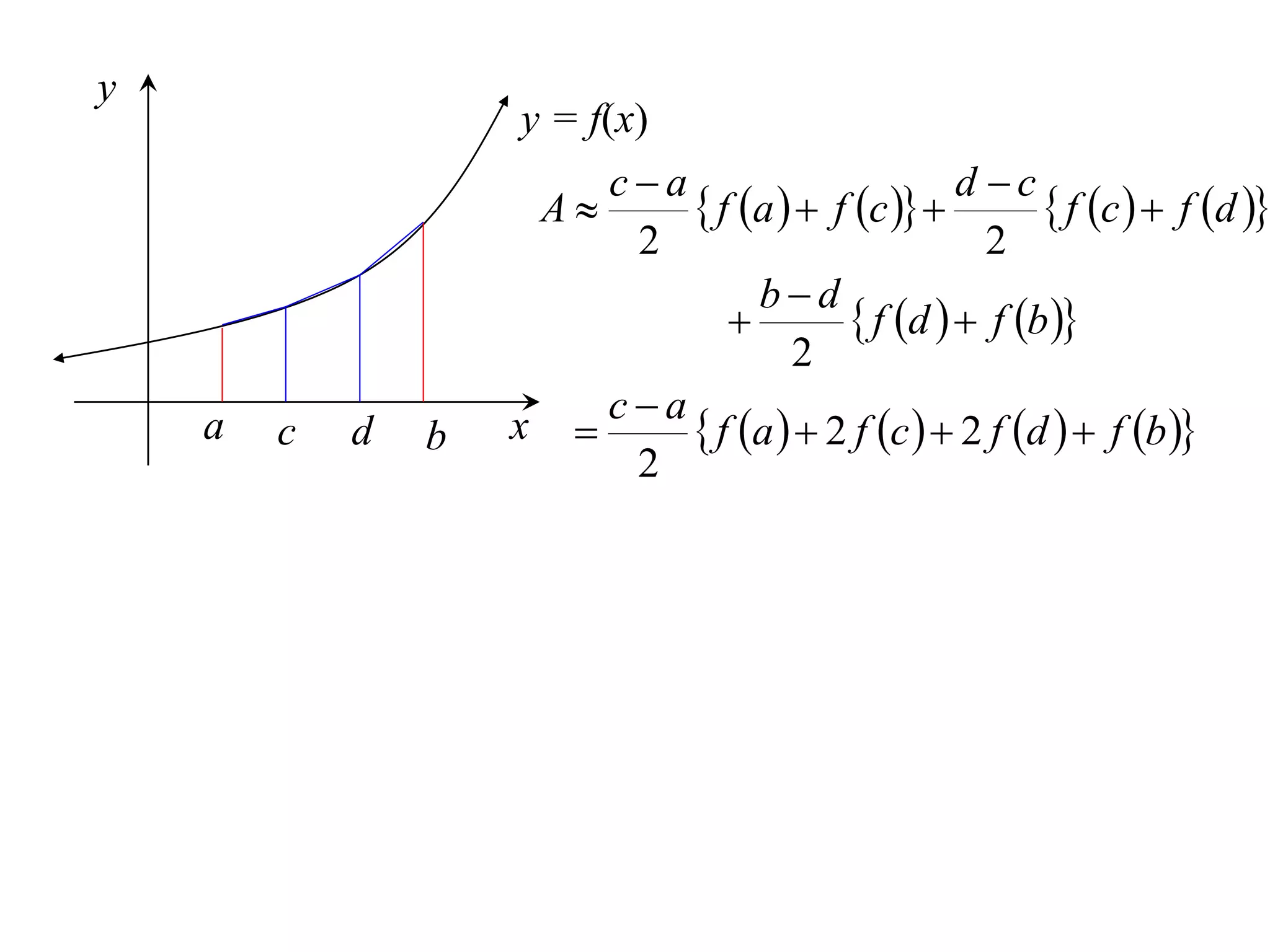
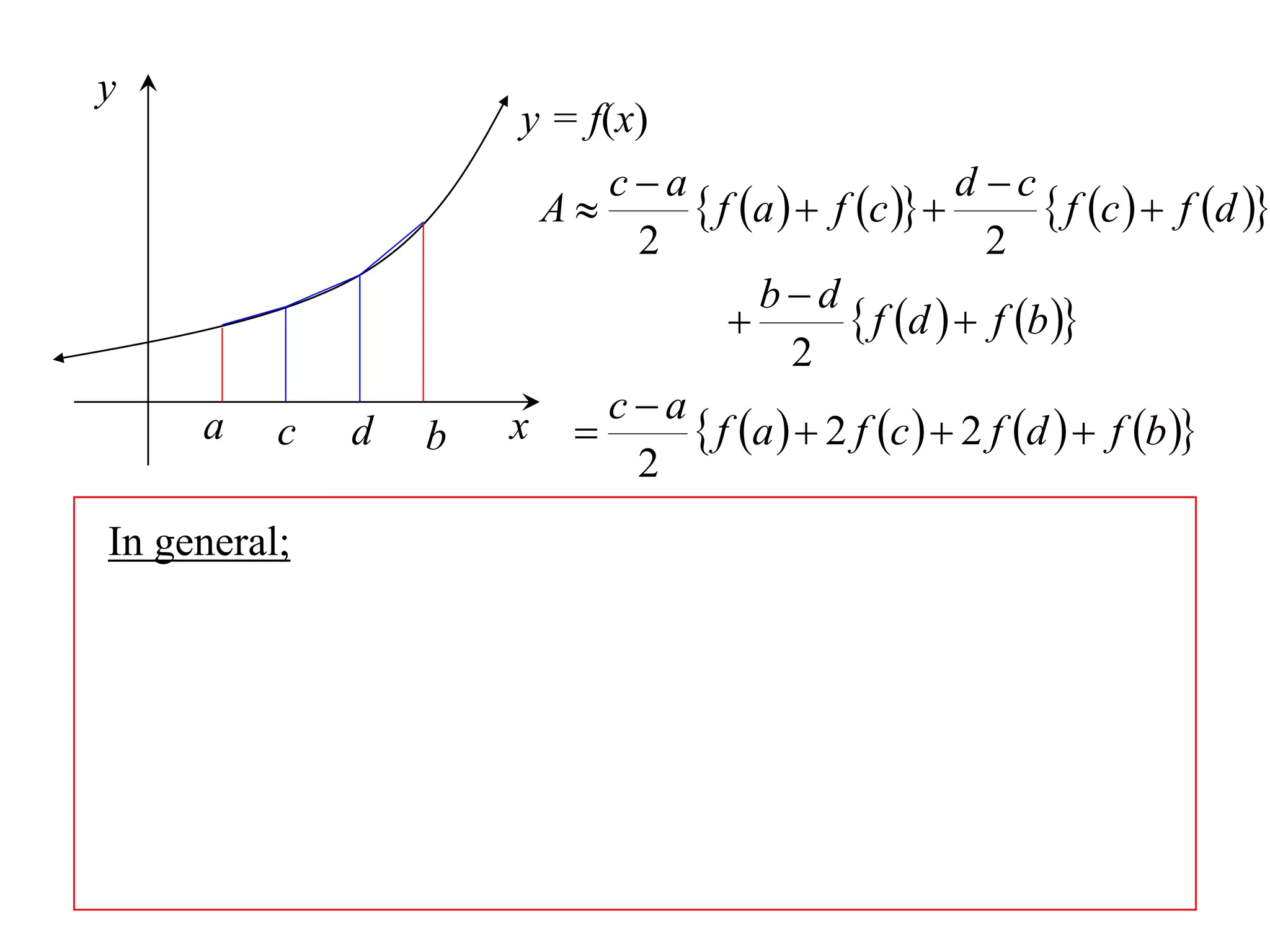
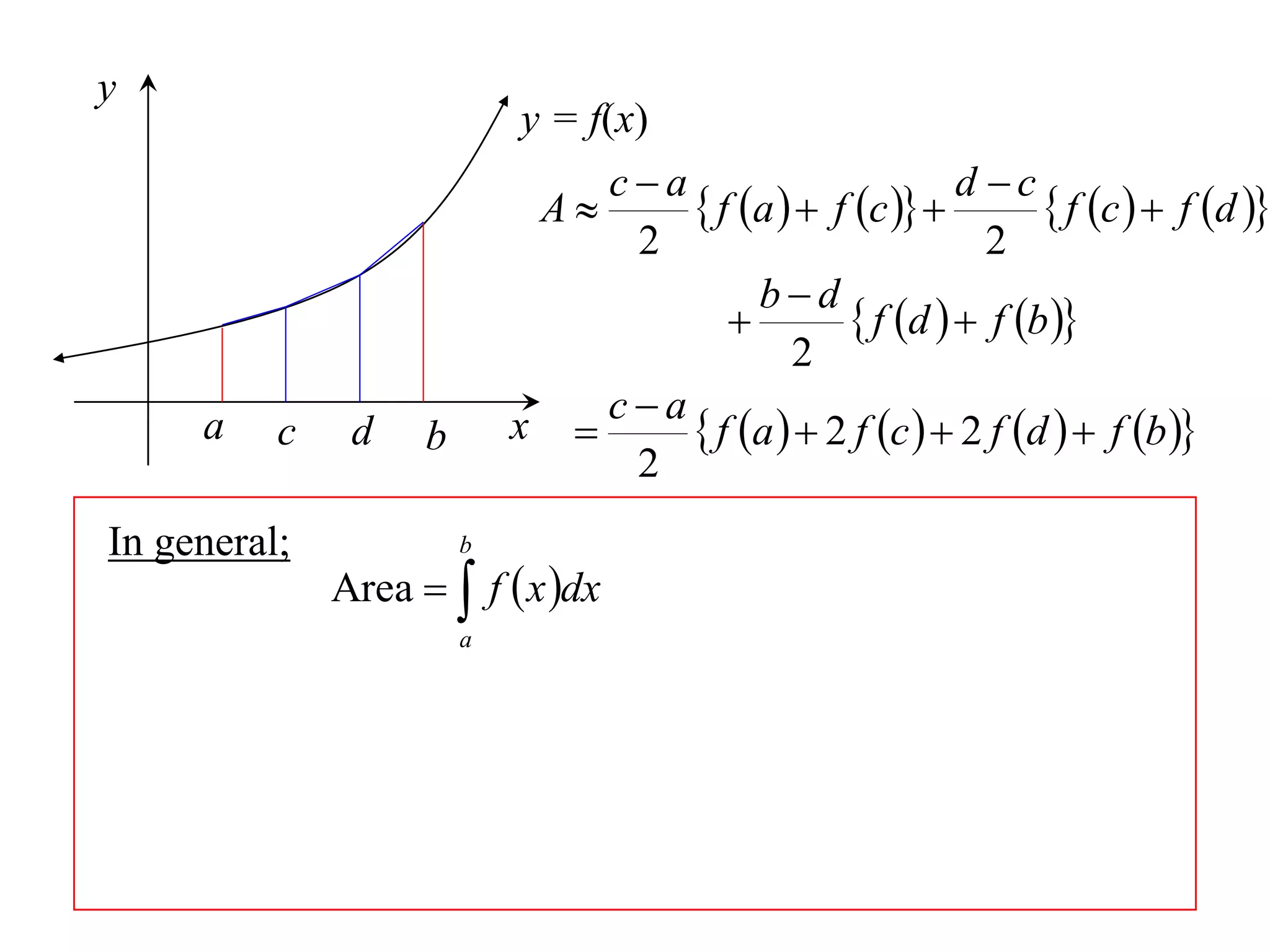
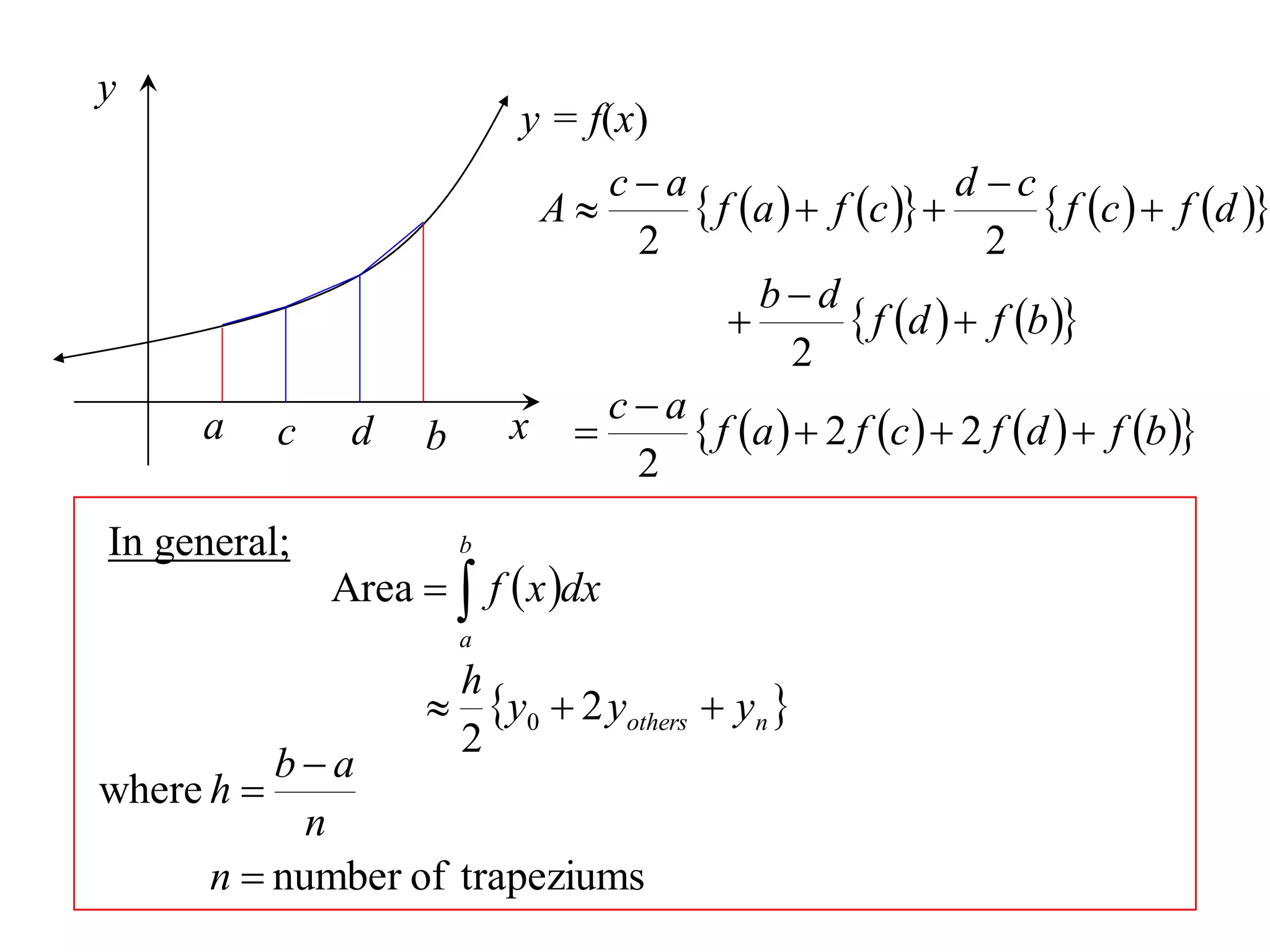
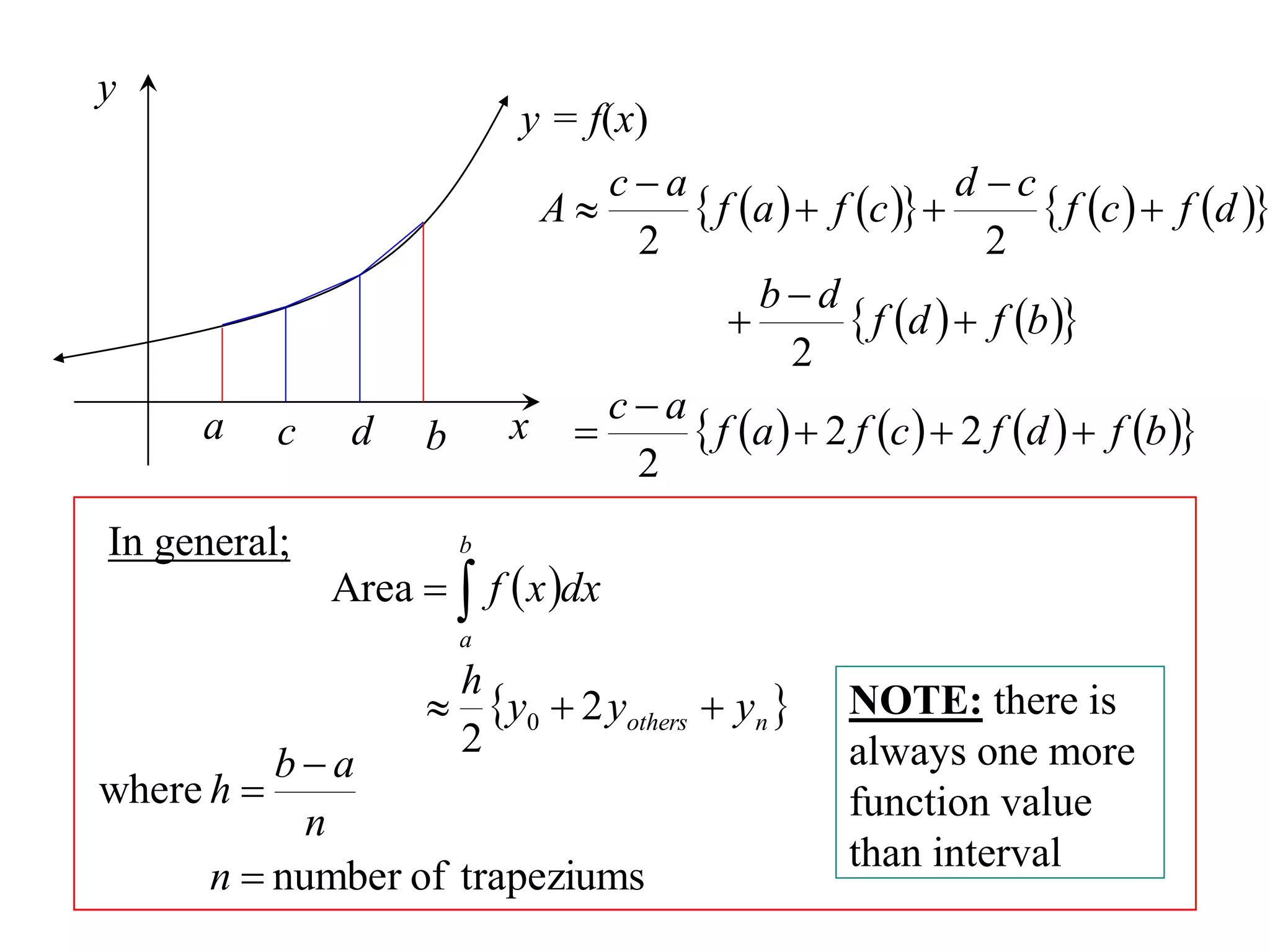
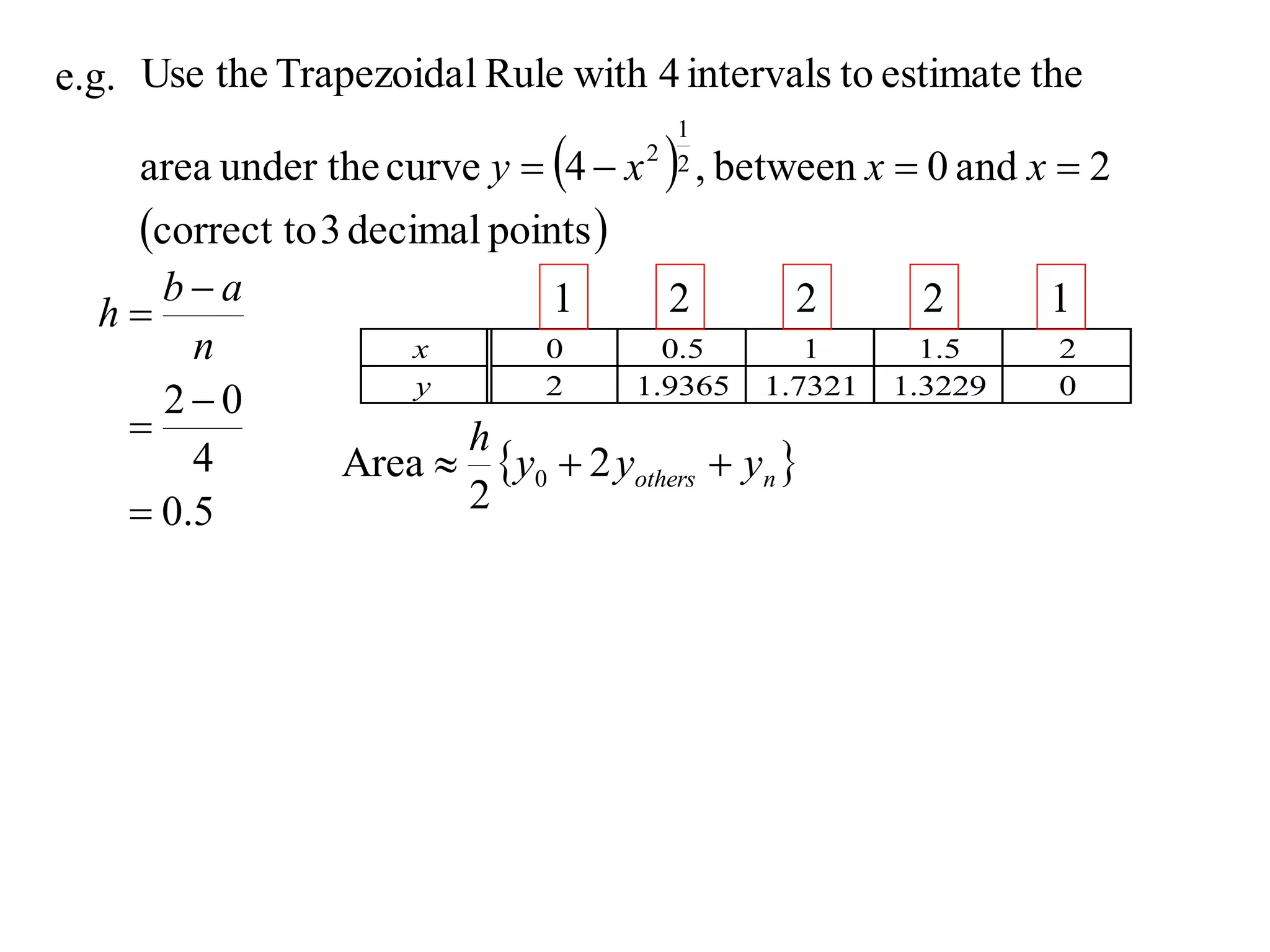
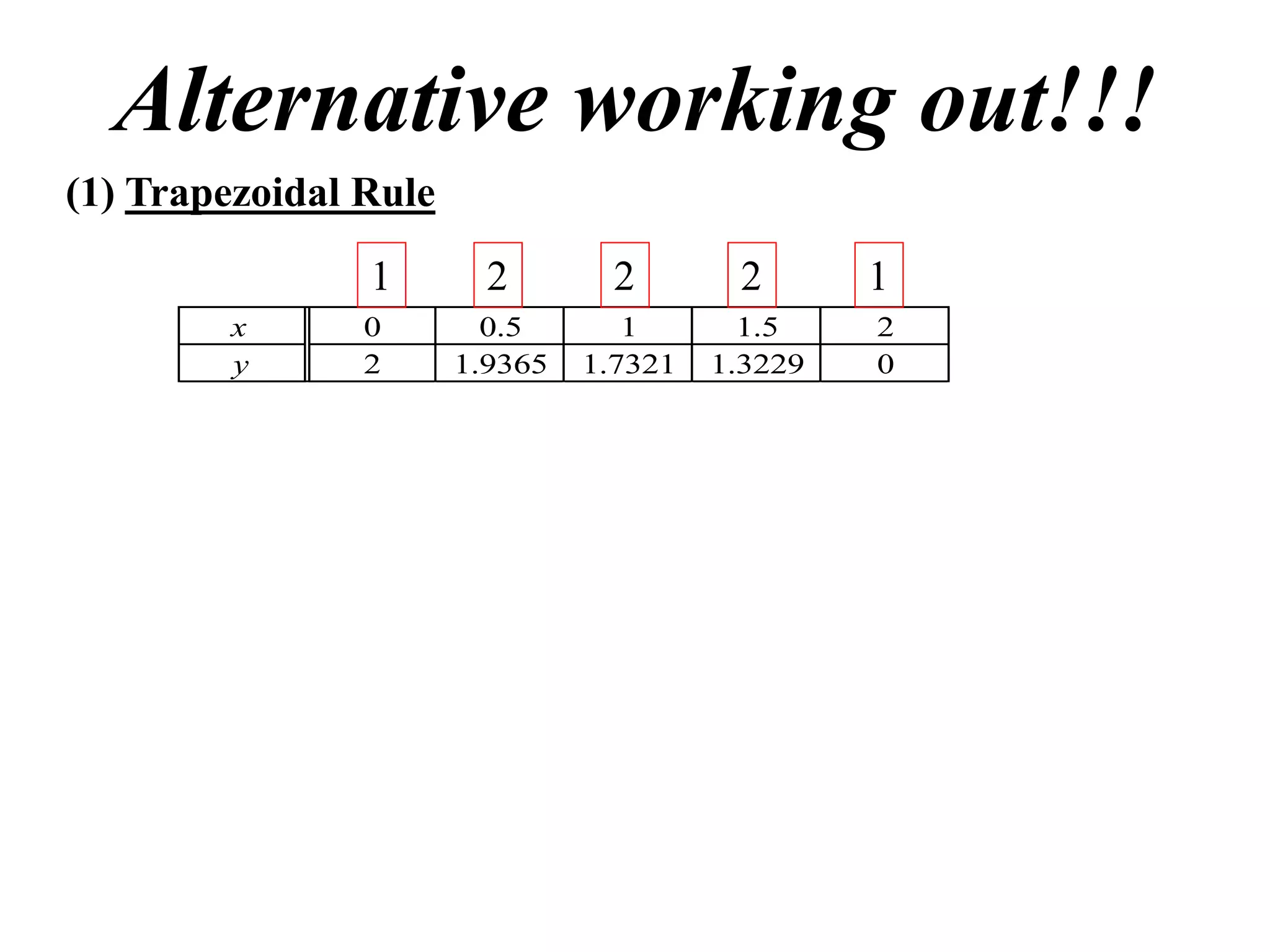
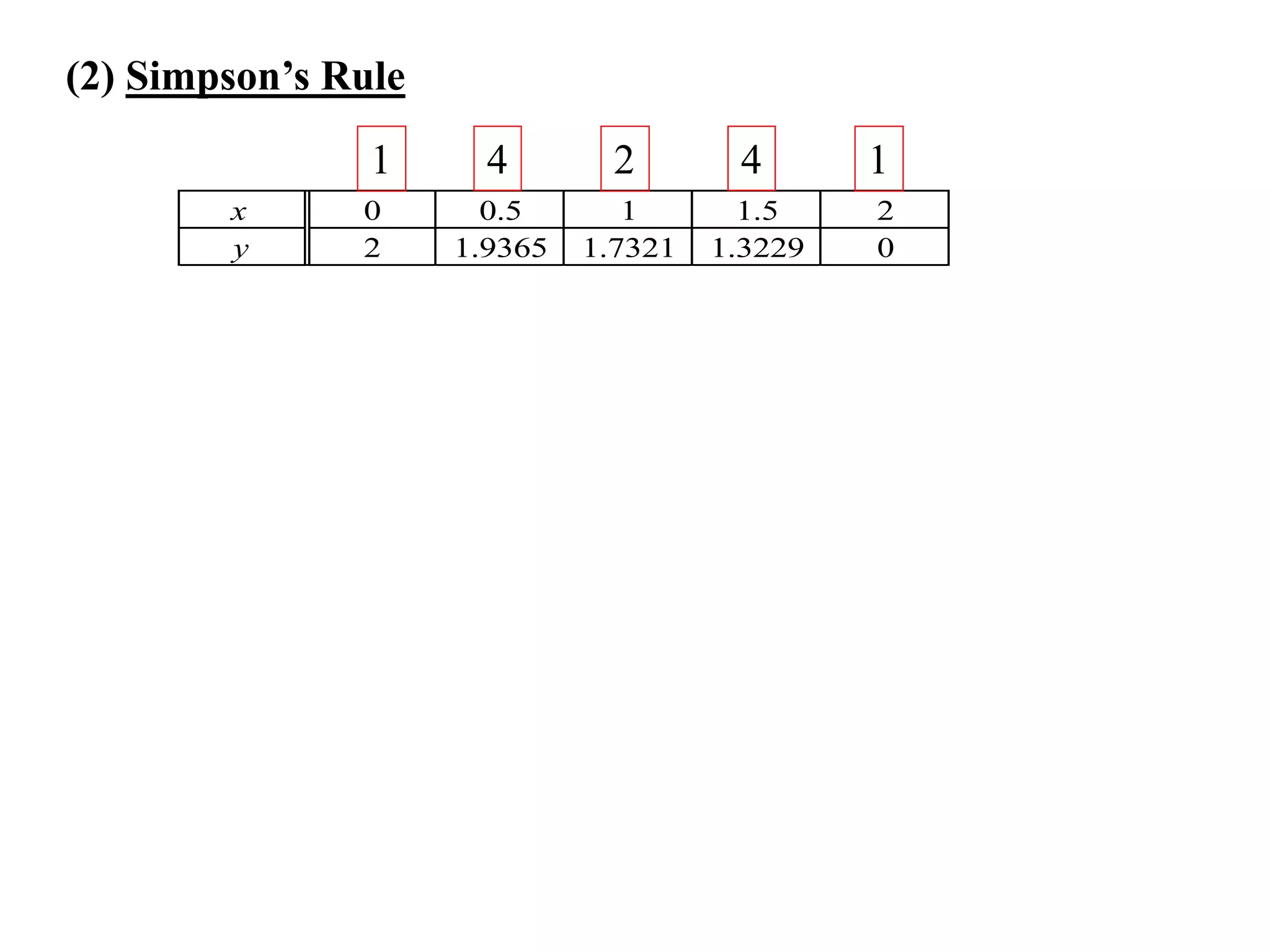
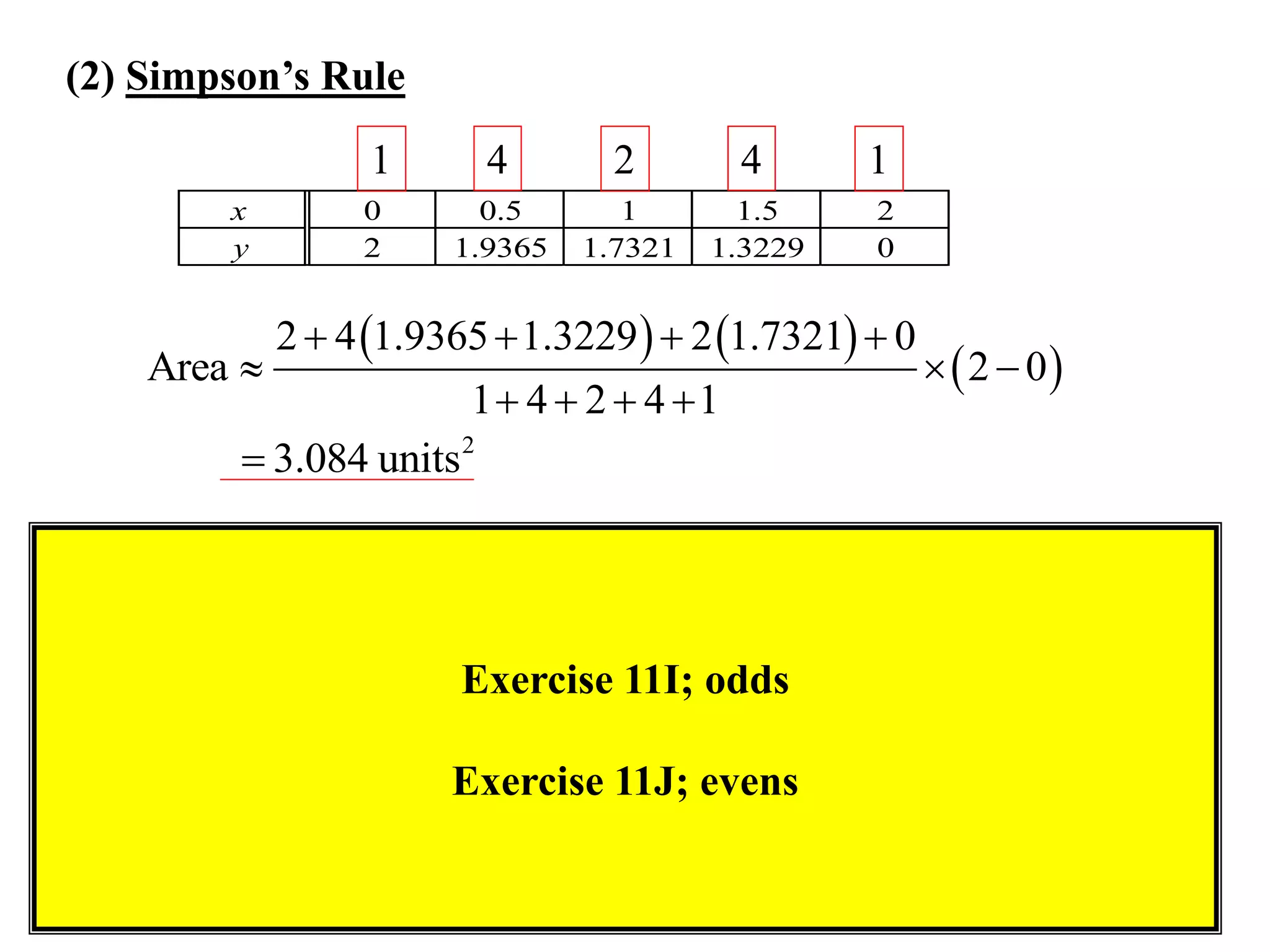
The document describes the Trapezoidal Rule for approximating the area under a curve between two points. It shows that the area A is estimated by dividing the region into trapezoids with height equal to the function values at the interval endpoints and bases equal to the intervals. In general, the area is approximated as the sum of the areas of each trapezoid, which is equal to the average of the endpoint function values multiplied by the interval length.

1. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
a
b
x

2. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
a
b
x

3. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
a
b
x
ba
A
 f a   f b 
2

4. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
ba
A
 f a   f b 
2
y
a
b
y = f(x)
x
a
b
x

5. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
ba
A
 f a   f b 
2
y
a
b
y = f(x)
x
a
c
b
x

6. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
ba
A
 f a   f b 
2
y
a
b
y = f(x)
x
ca
bc
A
 f a   f c  
 f c   f b 
2
2
a
c
b
x

7. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
ba
A
 f a   f b 
2
y
a
b
y = f(x)
x
ca
bc
A
 f a   f c  
 f c   f b 
2
2
ca

 f a   2 f c   f b 
2
a
c
b
x

8. y
y = f(x)
a
b
x

9. y
y = f(x)
a
c
d
b
x

10. y
y = f(x)
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
a
c
d
b
x

11. y
y = f(x)
a
c
d
b
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2

12. y
y = f(x)
a
c
In general;
d
b
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2

13. y
y = f(x)
a
c
In general;
d
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2
b
b
Area   f  x dx
a

14. y
y = f(x)
a
c
In general;
d
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2
b
b
Area   f  x dx
a
h
 y0  2 yothers  yn 
2

15. y
y = f(x)
a
c
In general;
d
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2
b
b
Area   f  x dx
a
h
 y0  2 yothers  yn 
2
ba
n
n  number of trapeziums
where h 

16. y
y = f(x)
a
c
In general;
d
ca
d c
A
 f a   f c  
 f c   f d 
2
2
bd

 f d   f b 
2
x  c  a  f a   2 f c   2 f d   f b 
2
b
b
Area   f  x dx
a
h
 y0  2 yothers  yn 
2
ba
n
n  number of trapeziums
where h 
NOTE: there is
always one more
function value
than interval

17. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
 , between x  0 and x  2
1
2 2

18. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
 , between x  0 and x  2
1
2 2

19. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
x
y
0
2
 , between x  0 and x  2
1
2 2
0.5
1.9365
1
1.7321
1.5
1.3229
2
0

20. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
x
y
0
2
 , between x  0 and x  2
1
2 2
0.5
1.9365
1
1.7321
h
Area  y0  2 yothers  yn 
2
1.5
1.3229
2
0

21. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
 , between x  0 and x  2
1
2 2
1
x
y
0
2
1
0.5
1.9365
1
1.7321
h
Area  y0  2 yothers  yn 
2
1.5
1.3229
2
0

22. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
1
x
y
0
2
 , between x  0 and x  2
1
2 2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  2 yothers  yn 
2

23. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
1
x
y
0
2
 , between x  0 and x  2
1
2 2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  2 yothers  yn 
2
0.5

2  21.9365  1.7321  1.3229  0
2
 2.996 units 2

24. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
1
x
y
0
2
 , between x  0 and x  2
1
2 2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  2 yothers  yn 
2
0.5

2  21.9365  1.7321  1.3229  0
2
exact value  π 
 2.996 units 2

25. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x
correct to 3 decimal points 
ba
h
n
20

4
 0.5
1
x
y
0
2
 , between x  0 and x  2
1
2 2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  2 yothers  yn 
2
0.5

2  21.9365  1.7321  1.3229  0
2
exact value  π 
 2.996 units 2
3.142  2.996
100
3.142
 4.6%
% error 

26. (2) Simpson’s Rule

27. (2) Simpson’s Rule
b
Area   f  x dx
a

28. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3

29. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 

30. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
e.g.
x
y
0
2
0.5
1.9365
1
1.7321
1.5
1.3229
2
0

31. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
e.g.
x
y
0
2
0.5
1.9365
1
1.7321
h
Area  y0  4 yodd  2 yeven  yn 
3
1.5
1.3229
2
0

32. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
1
e.g.
x
y
0
2
1
0.5
1.9365
1
1.7321
h
Area  y0  4 yodd  2 yeven  yn 
3
1.5
1.3229
2
0

33. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
1
e.g.
x
y
4
0
2
0.5
1.9365
4
1
1.7321
h
Area  y0  4 yodd  2 yeven  yn 
3
1
1.5
1.3229
2
0

34. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
1
e.g.
x
y
4
2
4
1
0
2
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  4 yodd  2 yeven  yn 
3

35. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
1
e.g.
x
y
4
2
4
1
0
2
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  4 yodd  2 yeven  yn 
3
0.5

2  41.9365  1.3229  21.7321  0
3
 3.084 units 2

36. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
n
n  number of intervals
where h 
1
e.g.
x
y
4
2
4
1
0
2
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
h
Area  y0  4 yodd  2 yeven  yn 
3
0.5

2  41.9365  1.3229  21.7321  0 3.142  3.084
3
% error 
100
3.142
 3.084 units 2
 1.8%

37. Alternative working out!!!
(1) Trapezoidal Rule

38. Alternative working out!!!
(1) Trapezoidal Rule
1
x
y
0
2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0

39. Alternative working out!!!
(1) Trapezoidal Rule
1
x
y
Area 
0
2
2
2
2
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
2  2 1.9365  1.7321  1.3229   0
1 2  2  2 1
 2.996 units 2
  2  0

40. (2) Simpson’s Rule
1
x
y
0
2
4
2
4
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0

41. (2) Simpson’s Rule
1
x
y
Area 
0
2
4
2
4
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
2  4 1.9365  1.3229   2 1.7321  0
1 4  2  4 1
 3.084 units 2
  2  0

42. (2) Simpson’s Rule
1
x
y
Area 
0
2
4
2
4
1
0.5
1.9365
1
1.7321
1.5
1.3229
2
0
2  4 1.9365  1.3229   2 1.7321  0
1 4  2  4 1
 3.084 units 2
Exercise 11I; odds
Exercise 11J; evens
  2  0