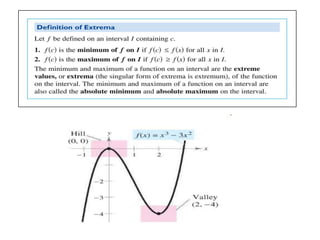
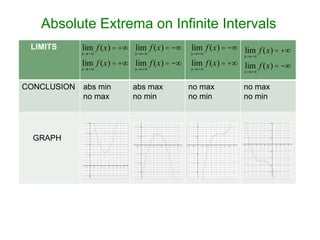
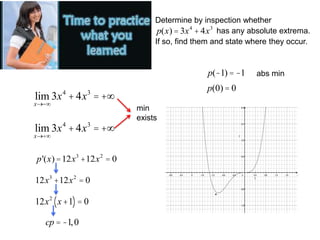
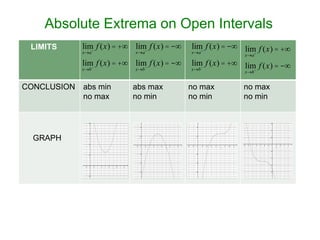
The document provides information on finding absolute maximum and minimum values (absolute extrema) of functions on different interval types. It discusses determining absolute extrema on closed, infinite, and open intervals. Examples are provided finding the absolute extrema of specific functions on given intervals, including finding any critical points and limits to determine if absolute extrema exist. Practice problems are also provided at the end to find the absolute extrema of additional functions on specified intervals.

1. Absolute Maxima and Minima

3. Absolute Extrema on Closet Intervals [ a, b ]

4. 4
3
1
3
Find the absolute extrema of f (x) = 6x - 3x
on the interval [ -1, 1 ], and determine where
these values occur.
1
3
f '(x) = 8x - x
-2
3
=x
-2
3
(8x -1)
(8x -1)
f '(x) =
x
f (-1) = 9
2
3
abs. max
f (0) = 0
Points to consider:
æ1ö
9
f ç ÷=è8ø
8
1/8
critical points
0
-1
endpoints of the interval
1
f (1) = 3
abs. min

5. Absolute Extrema on Infinite Intervals
LIMITS
lim f (x) = +¥ lim f (x) = -¥
x®-¥
x®-¥
lim f (x) = +¥ lim f (x) = -¥
x®+¥
CONCLUSION
GRAPH
abs min
no max
x®+¥
abs max
no min
lim f (x) = -¥ lim f (x) = +¥
x®-¥
x®-¥
lim f (x) = +¥ lim f (x) = -¥
x®+¥
no max
no min
x®+¥
no max
no min

6. Determine by inspection whether
p(x) = 3x 4 + 4x 3 has any absolute extrema.
If so, find them and state where they occur.
p(-1) = -1
p(0) = 0
lim 3x + 4x = +¥
4
3
x®-¥
lim 3x 4 + 4x 3 = +¥
min
exists
x®+¥
p'(x) =12x 3 +12x 2 = 0
12x 3 +12x 2 = 0
12x ( x +1) = 0
2
cp = -1, 0
·
abs min

7. Absolute Extrema on Open Intervals
lim f (x) = +¥ lim f (x) = -¥
+
x®a+
lim f (x) = +¥ lim f (x) = -¥
-
LIMITS
x®b-
x®a+
x®b-
CONCLUSION
GRAPH
abs min
no max
x®a
x®b
abs max
no min
lim f (x) = -¥ lim f (x) = +¥
+
x®a
lim f (x) = +¥ lim f (x) = -¥
-
no max
no min
x®b
no max
no min

8. Determine by inspection whether
p(x) =
1
x2 - x
has any absolute extrema
On the interval ( 0, 1 ). If so, find them and
state where they occur.
1
1
lim 2
= lim
= -¥
+
+
x®0 x - x
x®0 x x -1
( )
1
1
lim 2
= lim
= -¥
x®1 x - x
x®1 x x -1
( )
f '(x) = -
2x -1
(x
2
1
cp = 0, ,1
2
- x)
2
max
exists
f (0) = DNE
æ1ö
f ç ÷ = -4
è2ø
f (1) = DNE
=0
·

9. How about some
practice?
Find the absolute extrema for the following:
1. f (x) =1+
1
x
( 0,+¥)
2. f (x) = x 3e-2 x
[1, 4]
3. f (x) = sin x - cos x
( 0, p ]