Embed presentation
Download to read offline

![Absolute Extrema on Closet Intervals [ a, b ]](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-3-320.jpg)
![4
3
1
3
Find the absolute extrema of f (x) = 6x - 3x
on the interval [ -1, 1 ], and determine where
these values occur.
1
3
f '(x) = 8x - x
-2
3
=x
-2
3
(8x -1)
(8x -1)
f '(x) =
x
f (-1) = 9
2
3
abs. max
f (0) = 0
Points to consider:
æ1ö
9
f ç ÷=è8ø
8
1/8
critical points
0
-1
endpoints of the interval
1
f (1) = 3
abs. min](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-4-320.jpg)
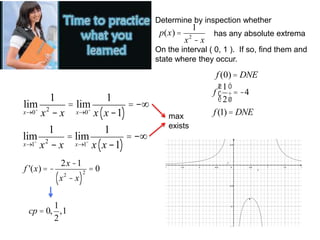
![How about some
practice?
Find the absolute extrema for the following:
1. f (x) =1+
1
x
( 0,+¥)
2. f (x) = x 3e-2 x
[1, 4]
3. f (x) = sin x - cos x
( 0, p ]](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-9-320.jpg)
The document provides information on finding absolute maximum and minimum values (absolute extrema) of functions on different interval types. It discusses determining absolute extrema on closed, infinite, and open intervals. Examples are provided finding the absolute extrema of specific functions on given intervals, including finding any critical points and limits to determine if absolute extrema exist. Practice problems are also provided at the end to find the absolute extrema of additional functions on specified intervals.


![Absolute Extrema on Closet Intervals [ a, b ]](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-3-320.jpg)
![4
3
1
3
Find the absolute extrema of f (x) = 6x - 3x
on the interval [ -1, 1 ], and determine where
these values occur.
1
3
f '(x) = 8x - x
-2
3
=x
-2
3
(8x -1)
(8x -1)
f '(x) =
x
f (-1) = 9
2
3
abs. max
f (0) = 0
Points to consider:
æ1ö
9
f ç ÷=è8ø
8
1/8
critical points
0
-1
endpoints of the interval
1
f (1) = 3
abs. min](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-4-320.jpg)




![How about some
practice?
Find the absolute extrema for the following:
1. f (x) =1+
1
x
( 0,+¥)
2. f (x) = x 3e-2 x
[1, 4]
3. f (x) = sin x - cos x
( 0, p ]](https://image.slidesharecdn.com/5-131206204936-phpapp01/85/5-4-absolute-maxima-and-minima-9-320.jpg)