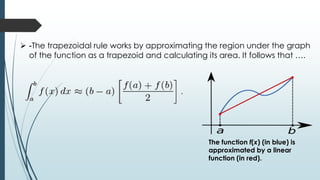
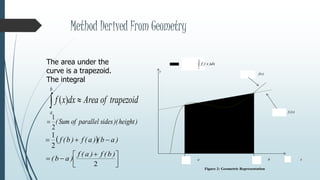
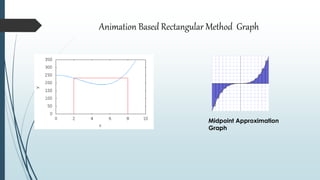
The document discusses the Newton-Cotes integration method, which provides numerical integration formulas using equally spaced points for the evaluation of integrands. It details closed and open types of Newton-Cotes formulas, including specific rules like the trapezoidal rule and Simpson's rule, alongside their applications and error analyses. The document also presents examples to illustrate the application of these methods in practical scenarios.

1. Newton Cotes Integration Method
Prepared By:- Pabari Shashikant.

2. INTRODUCTION
 -In numerical analysis, the Newton–Cotes formulae, also called the Newton–Cotes
quadrature rules or simply Newton–Cotes rules, are a group of formulae for
numerical integration(also called quadrature) based on evaluating the integrand at
equally spaced points.
 -They are named after Isaac Newton and Roger Cotes.
 -Newton–Cotes formulae can be useful if the value of the integrand
at equally spaced points is given.

3. DESCRIPTION
 It is assumed that the value of a function ƒ defined on [a, b] is known at
equally spaced points xi, for i = 0, …, n, where x0 = a and xn = b.
 Solved Using Newton-Cotes Formulae
 There are two types of Newton–Cotes formulae,
1)The "closed" type.
2)The "open" type.

4. the closed newton-cotes formulae
 In this type which uses the function value at all ʆ points.
 The closed Newton–Cotes formula of degree n is stated as…
 b n
∫ f(x) dx = ∑ wi.f(xi)
a i=0
 where xi = h i + x0, with h (called the step size) equal to (xn − x0) / n = (b −
a) / n.
 The wi are called weights.

5. Closed Newton–Cotes Formulae
Degree Common name Formula Error term
1 Trapezoid rule
2 Simpson's rule
3 Simpson's 3/8 rule
4 Boole's rule

6. Trapezoid rules
 Trapezoidal Rule is based on the Newton-Cotes Formula that states if one can
approximate the integrand as an nth order polynomial
 Then the integral of that function is approximated by the integral of that nth
order polynomial.
 Trapezoidal Rule assumes n=1, that is, the area under the linear polynomial,

7.  -The trapezoidal rule works by approximating the region under the graph
of the function as a trapezoid and calculating its area. It follows that ….
The function f(x) (in blue) is
approximated by a linear
function (in red).

8. Error analysis
 The error of the composite trapezoidal rule is the difference between
the value of the integral and the numerical result.
 here exists a number ξ between a and b, such that

9. Method Derived From Geometry
The area under the
curve is a trapezoid.
The integral
trapezoidofAreadxxf
b
a
 )(
)height)(sidesparallelofSum(
2
1

  )ab()a(f)b(f 
2
1



 

2
)b(f)a(f
)ab(
Figure 2: Geometric Representation
f(x)
a b

b
a
dx)x(f1
y
x
f1(x)

10. Example 1
The vertical distance covered by a rocket from t=8 to t=30
seconds is given by:
a) Use single segment Trapezoidal rule to find the distance
covered.
b) Find the true error, for part (a).
c) Find the absolute relative true error, for part (a).
tE
a
 











30
8
8.9
2100140000
140000
ln2000 dtt
t
x

11. Solution



 

2
)()(
)(
bfaf
abIa)
8a 30b
t
t
tf 8.9
2100140000
140000
ln2000)( 





)8(8.9
)8(2100140000
140000
ln2000)8( 






f
)30(8.9
)30(2100140000
140000
ln2000)30( 






f
sm /27.177
sm /67.901

12. Solution (cont)



 

2
67.90127.177
)830(I
m11868
a)
b) The exact value of the above integral is
 











30
8
8.9
2100140000
140000
ln2000 dtt
t
x m11061

13. Solution (cont)
b) ValueeApproximatValueTrueEt 
1186811061 
m807
c) The absolute relative true error, , would bet
100
11061
1186811061


t %2959.7

14. Open Newton–Cotes Formulas
Common
name
step size
Formula Error term
Degree
Rectangle rule,
or
midpoint rule
2
Trapezoid
method
3
Milne's rule 4
No Name 5

15. The Open Newton-Cotes formula
 In this type which not use the function values at the endpoints.
 b n-1
∫ f(x) dx = ∑ wi.f(xi)
a i=1
 The weights are found in a manner similar to the closed formula.

16. rectangular rules
 The rectangle method also called the midpoint or mid-ordinate rule.
 It computes an approximation to a definite integral, made by finding the area
of a collection of rectangles whose heights are determined by the values of the
function.
 Formula:- (b - a) f1

17.  Specifically, the interval over which the function is to be integrated is divided
into equal sub intervals of length.
 The rectangles are then drawn so that either their left or right corners, or the
middle of their top line lies on the graph of the function, with bases running along
the –axis,,,
 Giving formula are,,,,,
 where h=(b - a) / N And Xn=a + nh
The formula for above gives for the Top-left corner approximation.

18. Animation Based Rectangular Method Graph
Midpoint Approximation
Graph

19. Error Analysis
 For a function which is twice differentiable, the approximation error
in each section of the midpoint rule decays as the cube of the
width of the rectangle.
 for some in . Summing this, the approximation error for intervals with
width is less than or equal to
 N=1,2,3 where n + 1 is the number of nodes

20.  n terms of the total interval,we know that so we can rewrite the
expression:
 for some in (a,b).

21. Application of Simpson’s Rules
 Space
 Find the distance of the travel through velocity and interval of time
 Find the Volume of the solid
 Calculate amount of earth that must be moved to fill a depression
or make a dam.

22. The Velocity v(km/min) of a moped which starts from rest is given at
fixed intervals of time t(min) as follows:
 
km309.3372)2*804*(0
3
220
0tsdistancerequiredtheHence
725202018v8v6v4v2E
80211322510v9v7v5v3v1O
000v10v1X
etc.25v3,18v2,10v1,0v0,2hHere
20
0
rulesSimpson'by,2.E4.OX
3
h
dtv20
0ts
v
dt
ds
02511203229251810:v
2018161412108420:t





 

Estimate Approximately the distance covered in 20 minutes.
Sol. If s(km) be the distance covered in t(min), then
REAL TIME EXAMPLE OF SIMPSON’S METHOD