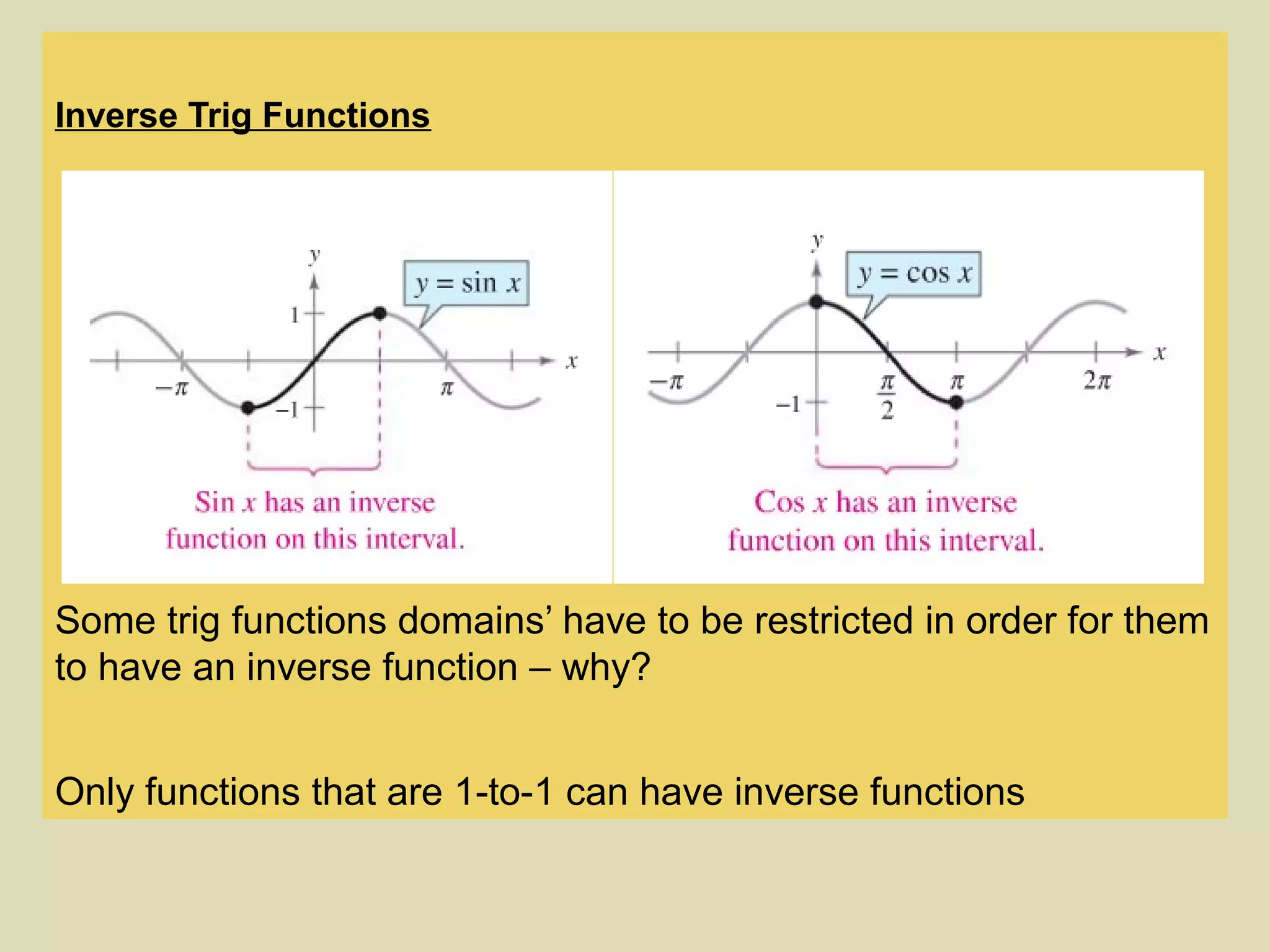
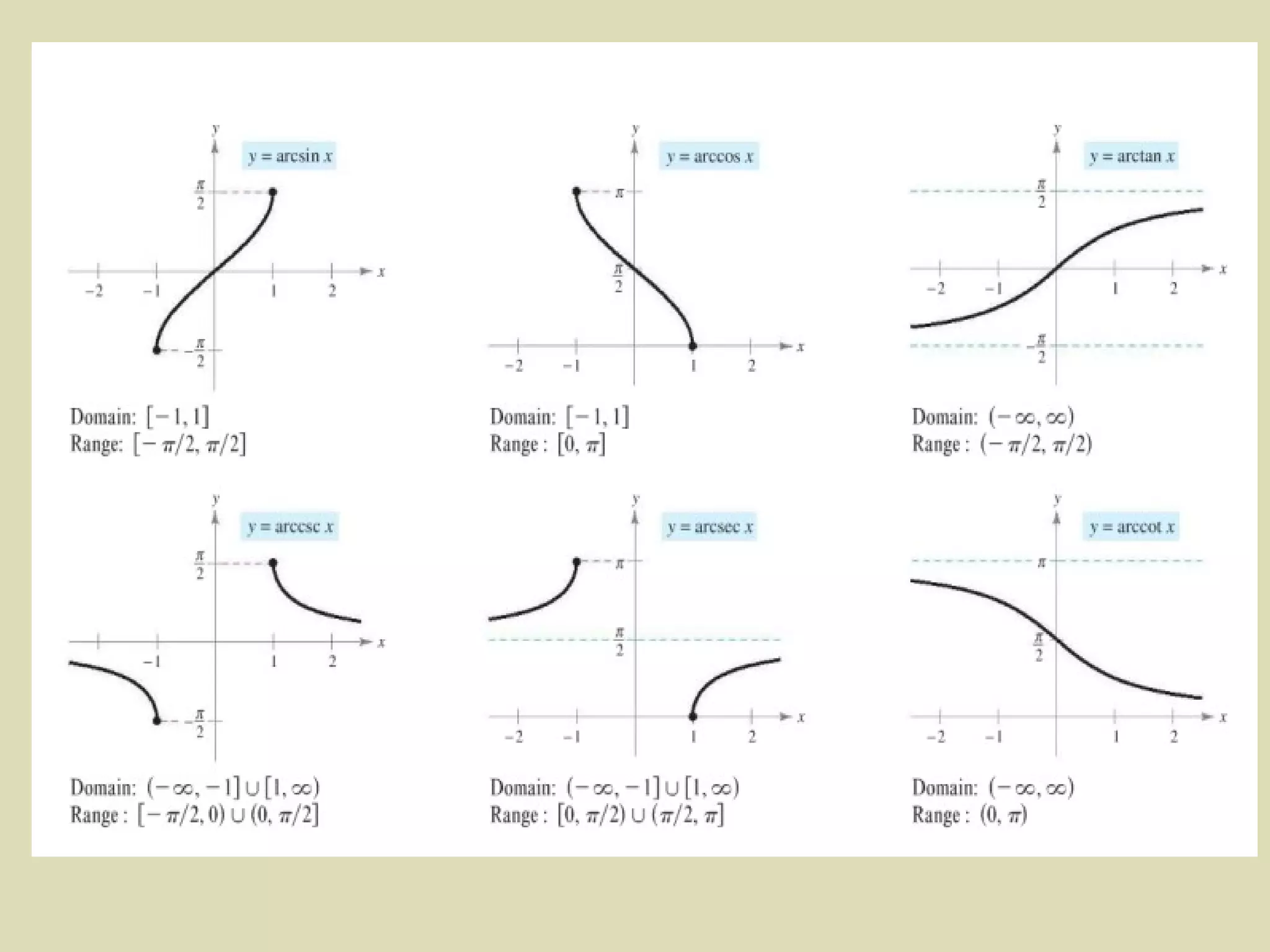
This document discusses derivatives of inverse trigonometric functions and differentiability of inverse functions. It provides examples of finding the derivative of inverse trig functions like sin^-1(x^3) and sec^-1(e^x). It also explains that if a function f(x) is differentiable on an interval I, its inverse f^-1(x) will also be differentiable if f'(x) is not equal to 0. It gives the formula for the derivative of the inverse function and an example confirming this formula. It also discusses monotonic functions and how if f'(x) is always greater than 0 or less than 0, f(x) is one-to-one and its inverse will be different

1. Derivatives of Inverse
Trigonometric Function

2. Inverse Trig Functions
Some trig functions domains’ have to be restricted in order for them
to have an inverse function – why?
Only functions that are 1-to-1 can have inverse functions

5. Find
dy
dx
If
y = sin −1 ( x 3 )
dy
1
=
×( 3x 2 )
dx
3 2
1− ( x )
therefore
3x 2 )
(
dy
=
dx
3 2
1− ( x )

6. One more example
Find
dy
dx
dy
=
dx e x
y = sec−1 ( e x )
if
1
(e )
x 2
−1
dy
1
=
dx
e 2 x −1
×( e x )

7. Differentiability of Inverse Functions
If f(x) is differentiable on an interval I, one may wonder whether f-1(x) is also
differentiable? The answer to this question hinges on f'(x) being equal to 0 or
not . Indeed, if for any , then f-1(x) is also differentiable. Moreover we have
Using Leibniz's notation, the above formula becomes
which is easy to remember.

8. Example:
Confirm Differentiability of Inverse Function formula for the
function f (x) = x 3 +1
Solution:
y = x 3 +1
x = y3 +1
y = x −1
3
x = 3 y −1
f −1 (y) = 3 y −1
dy d  3 
=  x + 1 = 3x 2
dx dx
and
1
2
dx d  3
d
1
−
=  y − 1 =  ( y − 1) 3  = ( y − 1) 3
 dy 
 3
dy dy
(
)
2
2
dy
1
3 y−1 = 3 y−1 3 =
=3
( ) dx
dx
dy

9. MONOTONIC
FUNCTIONS:
Suppose that the domain of a function f is on an open interval I on which
f’(x) > 0 or on which f’(x) < 0. Then f is one-to-one, f-1(x) is differentiable
at all values of x in the range of f.
Example:
Consider the function
f (x) = x 5 + x +1
Solution:
f '(x) = 5x 4 +1
Since f’(x) > 0 on the entire domain, f(x) is
monotonic, therefore it has an inverse
.Show that f(x) is one-to=one function.

10. MONOTONIC
FUNCTIONS:
Suppose that the domain of a function f is on an open interval I on which
f’(x) > 0 or on which f’(x) < 0. Then f is one-to-one, f-1(x) is differentiable
at all values of x in the range of f.
Example:
Consider the function
f (x) = x 5 + x +1
Solution:
f '(x) = 5x 4 +1
Since f’(x) > 0 on the entire domain, f(x) is
monotonic, therefore it has an inverse
.Show that f(x) is one-to=one function.