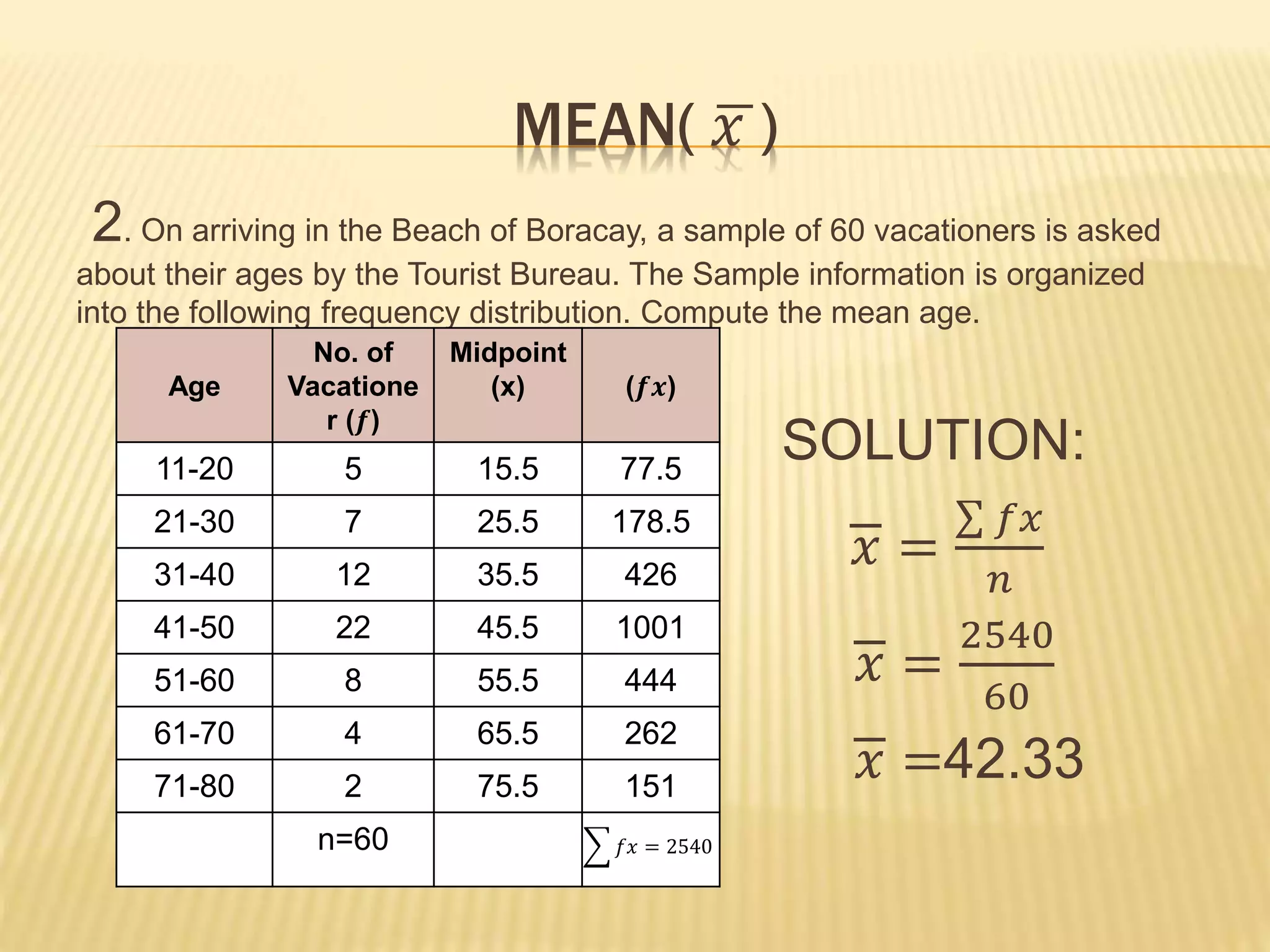
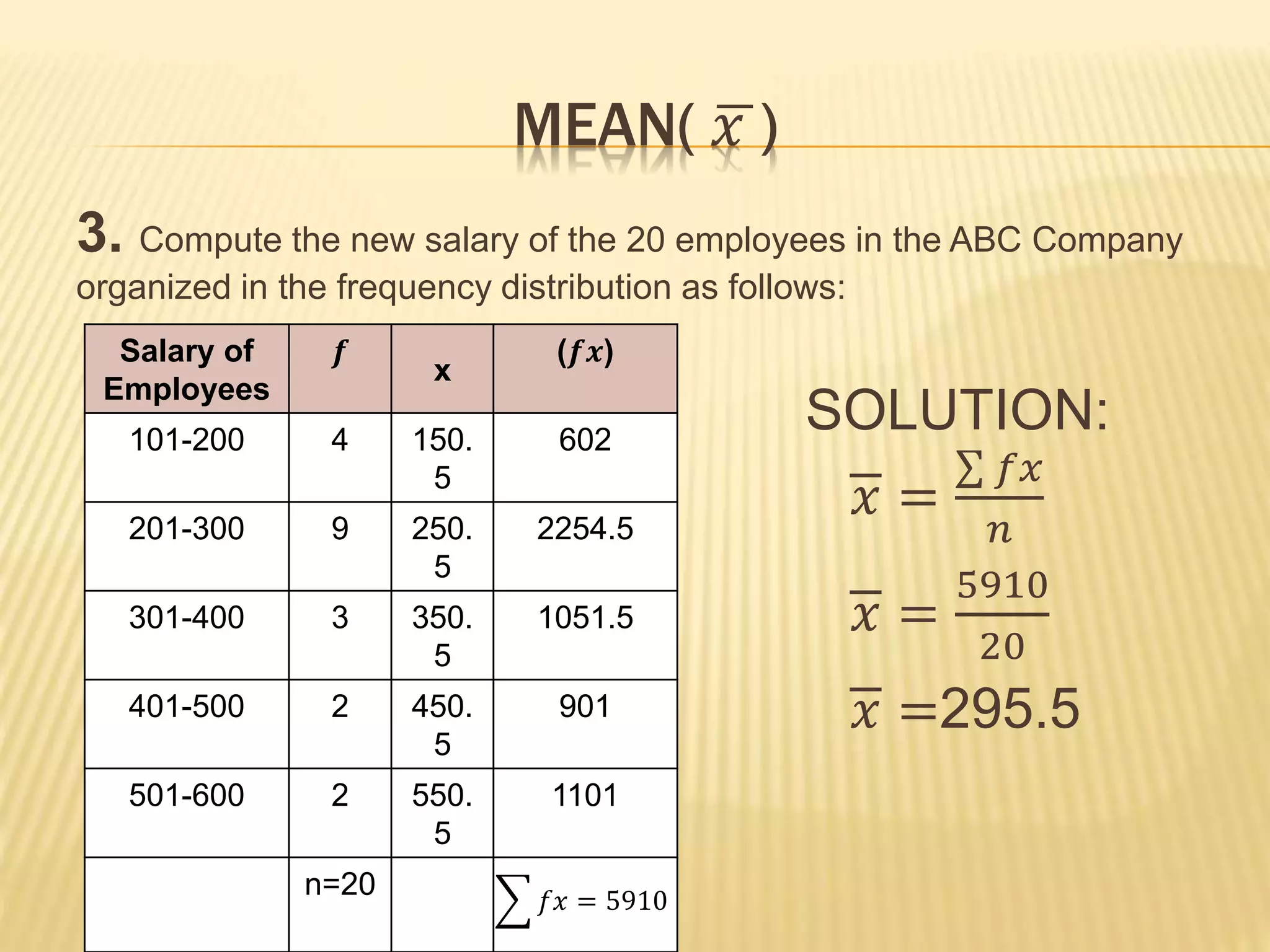
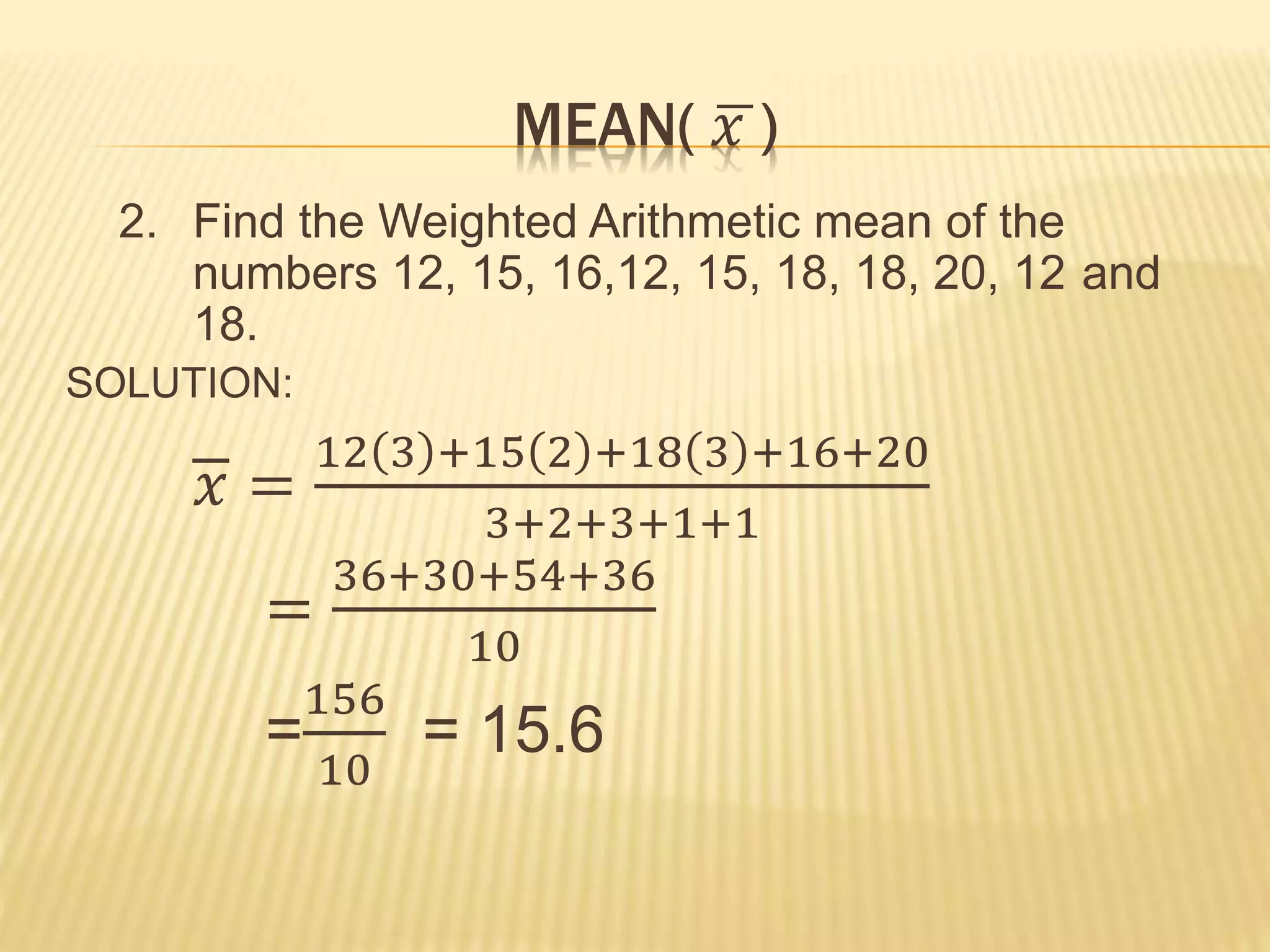This document provides formulas and examples for calculating the mean and median of data sets. It defines the mean as the sum of all values divided by the total number of data points. For grouped data, the mean is calculated as the sum of the frequency multiplied by the midpoint of each class, divided by the total number of data points. Examples are provided to demonstrate calculating the mean of both ungrouped and grouped data sets. The median is defined for grouped data as the lower boundary of the class containing the median plus the class width times the amount the cumulative frequency is less than the halfway point, divided by the total number of data points. An example is given to demonstrate calculating the median of a grouped data set.

1. NUMERICAL METHOD
REPORTED BY:
Angel Grace Adem

2. MEAN( 𝑥 )
FORMULA:
Ungrouped Data :
𝑥 =
𝑥1+𝑥2+⋯ 𝑥 𝑛
𝑛
Group Data:
𝑥 =
𝑓𝑥
𝑛
where: f = frequency in each class
x= midpoint of each class
n= total number of scores

3. MEAN( 𝑥 )
EXAMPLES (ungrouped Data):
1. Find the mean of 5, 7, 11, 20 and 18.
SOLUTION:
𝑥 =
5 + 7 + 11 + 20 + 18
5
=
61
5
= 12.2

4. MEAN( 𝑥 )
2. Find the Weighted Arithmetic mean of the
numbers 12, 15, 16,12, 15, 18, 18, 20, 12 and
18.
SOLUTION:
𝑥 =
12 3 +15 2 +18 3 +16+20
3+2+3+1+1
=
36+30+54+36
10
=
156
10
= 15.6

5. MEAN( 𝑥 )
3. The class standing of a student is 84,
while the preliminary examination is 75.
Compute the preliminary grade if the weighted
of the class standing is 2 and the preliminary
examination is 1.

6. MEAN( 𝑥 )
SOLUTION:
𝑥 =
2
3
84 +
1
3
79
=
168
3
+
79
3
=
247
3
= 82.33

7. MEAN( 𝑥 )
Example (grouped data):
1. SOLUTION:
𝑥 =
𝑓𝑥
𝑛
𝑥 =
186
33
𝑥 = 5.636 or
5.64
Interv
al
Midpoint Frequen
cy
(𝒇𝒙)
1-3 2 7 14
4-6 5 12 60
7-9 8 14 112
n=33 𝑓𝑥 = 186

8. MEAN( 𝑥 )
2. On arriving in the Beach of Boracay, a sample of 60 vacationers is asked
about their ages by the Tourist Bureau. The Sample information is organized
into the following frequency distribution. Compute the mean age.
SOLUTION:
𝑥 =
𝑓𝑥
𝑛
𝑥 =
2540
60
𝑥 =42.33
Age
No. of
Vacatione
r (𝒇)
Midpoint
(x) (𝒇𝒙)
11-20 5 15.5 77.5
21-30 7 25.5 178.5
31-40 12 35.5 426
41-50 22 45.5 1001
51-60 8 55.5 444
61-70 4 65.5 262
71-80 2 75.5 151
n=60 𝑓𝑥 = 2540

9. MEAN( 𝑥 )
3. Compute the new salary of the 20 employees in the ABC Company
organized in the frequency distribution as follows:
SOLUTION:
𝑥 =
𝑓𝑥
𝑛
𝑥 =
5910
20
𝑥 =295.5
Salary of
Employees
𝒇
x
(𝒇𝒙)
101-200 4 150.
5
602
201-300 9 250.
5
2254.5
301-400 3 350.
5
1051.5
401-500 2 450.
5
901
501-600 2 550.
5
1101
n=20 𝑓𝑥 = 5910

10. MEDIAN 𝑥
FORMULA
Grouped Data :
𝑥 = 𝐿 𝑏 +
𝑛
2
−𝐶𝐹<
𝑓 𝑚
∙ 𝑐
Where: 𝐿 𝑏 =lower class containing the median
𝐶𝐹< = less than cumulative frequency
𝑓𝑚 = frequency of the class containing median
c = width of the class
n = number of sample

11. MEDIAN 𝑥
FORMULA (ungrouped data):
𝑥 =
𝑛+1
2
Where:
n= number of sample

12. MEDIAN 𝑥
EXAMPLE 1.
Following distribution of Mathematics scores of 20 students:
𝒙 = 𝑳 𝒃 +
𝒏
𝟐
−𝑪𝑭<
𝒇 𝒎
∙ 𝑐
𝒙 = 4.5 +
𝟐𝟎
𝟐
−𝟒
𝟖
∙ 𝑐
𝒙 = 4.5 +
10−4
8
⋅ 2
𝒙 = 6
Scores
Number
of
Students
CF
1-2 1 1
3-4 3 4 𝐶𝐹< =
4
5-6 8 12 𝐿 𝑏 =
4.5
7-8 6 18
9-10 2 20