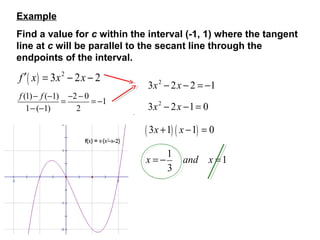
This document discusses Rolle's theorem and the mean value theorem. It provides the definitions and formulas for each theorem. It then gives examples of applying each theorem to find values of c where a derivative is equal to zero or a tangent line is parallel to a secant line. Rolle's theorem examples find values of c where the derivative of a function over an interval is zero. The mean value theorem examples find values of c where the slope of a tangent line equals the slope of a secant line over an interval.

1. Rolle’s Theorem
and Mean Value
Theorem

2. Theorem:

3. Example
π π 
 , 
Let f(x) = sin 2x. Find all values of c in the interval  6 3 
such that f’(c) = 0
Does it satisfy Rolle’s Theorem?
f is continuous
f is differentiable
π 
 π
π 
3
f  ÷= sin  2 × ÷= sin  ÷=
6
 6
3 2
π 
 π
 2π 
3
f  ÷= sin  2 × ÷= sin  ÷=
3
 3
 3  2
π 
π 
f  ÷= f  ÷
6
3
Find any c values:
f ' ( x ) = 2 cos ( 2x )
2 cos ( 2x ) = 0
cos ( 2x ) = 0
2x =
π
2
x=
π
4

4. Another Example:
2
Let f (x) = x − 5x + 4 . Find all values of c in the interval ( 1, 4)
such that f’(c) = 0
Does it satisfy Rolle’s Theorem?
Find any c values:

5. Theorem: Mean Value
Theorem
Let f be continuous on the
closed interval [a, b] and
differentiable on the open
interval (a, b). Then there is
at least one point c in (a, b)
such that
slope of
tangent at c
f ( b) − f ( a )
f ′( c ) =
b−a
slope of
secant over
the interval
[a, b]

6. Example
Find a value for c within the interval (-1, 1) where the tangent
line at c will be parallel to the secant line through the
endpoints of the interval.
f ′ ( x ) = 3x 2 − 2x − 2
f (1) − f (−1) −2 − 0
=
= −1
1− (−1)
2
3x 2 − 2x − 2 = −1
3x 2 − 2x −1 = 0
( 3x +1) ( x −1) = 0
x=−
1
3
and
x =1

7. Another Example
f ( x) =
1 3
x +1
4
Show that the function
satisfies the hypotheses of the
Mean-Value-Theorem over the interval [ 0, 2 ] , and find all values of c in the
interval (0, 2) at which the tangent line to the graph of f is parallel to the
secant line joining the endpoints of the interval
3 2
x
4
f ( 2 ) − f (0) 3 −1
=
=1
2−0
2
f '( x) =
3 2
x =1
4
4
x2 =
3
x =±
2
x=
3
2
3
x=−
2
3