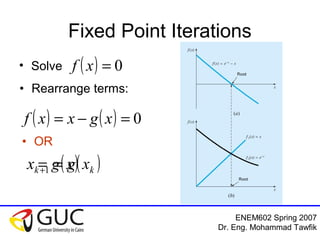
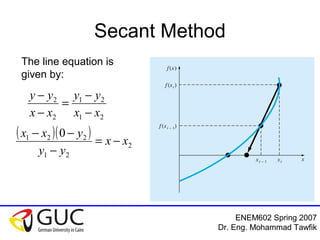
This document outlines numerical methods for finding roots of nonlinear equations presented by Dr. Eng. Mohammad Tawfik. It introduces the fixed point, Newton-Raphson, and secant methods. The fixed point method rearranges the equation to an iterative form where the next estimate is a function of the previous. Newton-Raphson linearizes the function to get faster convergence. The secant method does not require derivatives by using the slope between previous points. Convergence conditions and algorithms are provided for each method. Students are assigned homework problems from the textbook.

1. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Roots of Nonlinear Equations
Open Methods

2. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Objectives
• Be able to use the fixed point method to
find a root of an equation
• Be able to use the Newton Raphson
method to find a root of an equations
• Be able to use the Secant method to find a
root of an equations
• Write down an algorithm to outline the
method being used

3. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Fixed Point Iterations

4. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
( )kk xgx =+1
Fixed Point Iterations
• Solve ( ) 0=xf
( ) ( ) 0=−= xgxxf
• Rearrange terms:
• OR
( )xgx =

5. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
In some cases you do not get a
solution!

6. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example

7. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example
( ) 22
−−= xxxf Which has the solutions -1 & 2
To get a fixed-point form, we may use:
( ) 22
−= xxg
( ) x
xg 21+=
( ) 2+= xxg
( )
12
22
−
+
=
x
x
xg

8. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
First trial!
• No matter how close
your initial guess is,
the solution diverges!

9. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Second trial
• The solution converges
in this case!!

10. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Condition of Convergence
• For the fixed point iteration to ensure
convergence of solution from point xk we should
ensure that
( ) 1' <kxg

11. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Fixed Point Algorithm
1. Rearrange f(x) to get f(x)=x-g(x)
2. Start with a reasonable initial guess x0
3. If |g’(x0)|>=1, goto step 2
4. Evaluate xk+1=g(xk)
5. If (xk+1-xk)/xk+1< εs; end
6. Let xk=xk+1; goto step 4

12. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton-Raphson Method

13. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method: Line Equation
( )1
21
21
' xf
xx
yy
m =
−
−
=
The slope of the
line is given by:

14. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method: Line equation
( ) ( )1
21
1
' xf
xx
xf
=
−
( )
( )1
1
12
' xf
xf
xx −=
( )
( )k
k
kk
xf
xf
xx
'
1 −=+
Newton-Raphson
Iterative method

15. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method: Taylor’s Series
( ) ( ) ( )1121 ' xfxxxf −=−
( )
( )1
1
12
' xf
xf
xx −=
( )
( )k
k
kk
xf
xf
xx
'
1 −=+
Newton-Raphson
Iterative method
( ) ( ) ( ) ( )11212 ' xfxxxfxf −+≈

16. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example

17. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton-Raphson Algorithm
1. From f(x) get f’(x)
2. Start with a reasonable initial guess x0
3. Evaluate xk+1=xk-f(xk)/f’(xk)
4. If (xk+1-xk)/xk+1< εs; end
5. Let xk=xk+1; goto step 4

18. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Convergence condition!
• Try to derive a convergence conditions
similar to that of the fixed point iteration!

19. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Secant Method

20. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Secant Method
21
21
2
2
xx
yy
xx
yy
−
−
=
−
−
The line equation is
given by:
( )( )
2
21
221 0
xx
yy
yxx
−=
−
−−

21. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Secant Method
( )( )
2
21
221 0
xx
yy
yxx
−=
−
−−
( )
21
212
2
yy
xxy
xx
−
−
−=
( )( )
( ) ( )kk
kkk
kk
xfxf
xxxf
xx
−
−
−=
−
−
+
1
1
1

22. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Secant Algorithm
1. Select x1 and x2
2. Evaluate f(x1) and f(x2)
3. Evaluate xk+1
4. If (xk+1-xk)/xk+1< εs; end
5. Let xk=xk+1; goto step 3

23. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Why Secant Method?
• The most important advantage over
Newton-Raphson method is that you do
not need to evaluate the derivative!

24. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Comparing with False-Position
• Actually, false
position ensures
convergence, while
secant method does
not!!!

25. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Conclusion
• The fixed point iteration, Newton-Raphson
method, and the secant method in general
converge faster than bisection and false position
methods
• On the other hand, these methods do not ensure
convergence!
• The secant method, in many cases, becomes
more practical than Newton-Raphson as
derivatives do not need to be evaluated

26. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Homework #2
• Chapter 6, p 157, numbers:
6.1,6.2,6.3
• Homework due next week