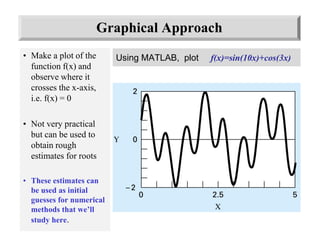
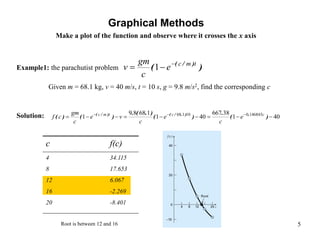
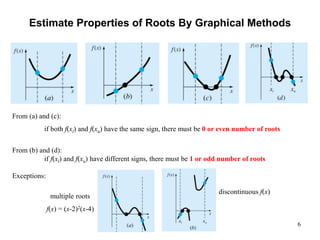
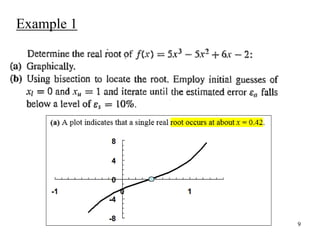
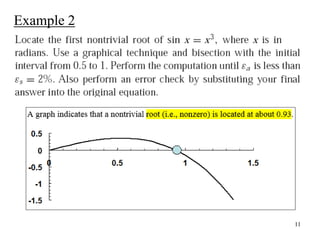
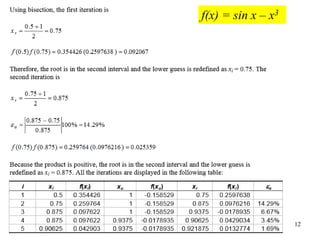
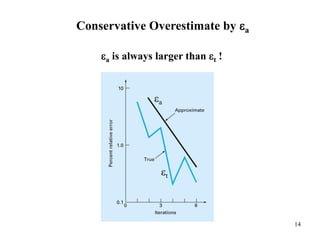
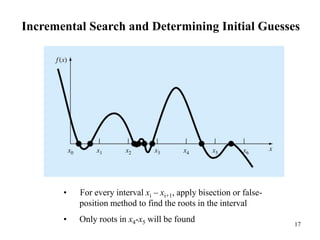
This document discusses the bracketing method for finding the roots of equations. It begins by introducing bracketing methods and noting that they require initial guesses that bracket a root. It then provides an example of using a graphical method to find the root of an equation by plotting the function and observing where it crosses the x-axis. Finally, it describes the bisection method in more detail, noting that it iteratively narrows the range containing the root until the desired accuracy is reached.

1. 1
Chapter 5
Bracketing Method

2. 2
• Easy
• But, not easy
• How about these?
a
acbb
xcbxax
2
4
0
2
2 


?02345
 xfexdxcxbxax
Roots of Equations
?0)3sin()10cos(
?0sin


xxx
xxx

3. Graphical Approach
• Make a plot of the
function f(x) and
observe where it
crosses the x-axis,
i.e. f(x) = 0
• Not very practical
but can be used to
obtain rough
estimates for roots
• These estimates can
be used as initial
guesses for numerical
methods that we’ll
study here.
Using MATLAB, plot f(x)=sin(10x)+cos(3x)

4. 4
Why Called Bracketing Methods?
They require two initial guesses which “bracket”
either side of the root.

5. 5
Example1: the parachutist problem
Given m = 68.1 kg, v = 40 m/s, t = 10 s, g = 9.8 m/s2, find the corresponding c
Graphical Methods
401
38667
401
16889
1 146843010168
 
)(
.
)(
).(.
)()( .)./()/( cctmc
e
c
e
c
ve
c
gm
cf
)( )/( tmc
e
c
gm
v 
 1
Make a plot of the function and observe where it crosses the x axis
Solution:
c f(c)
4 34.115
8 17.653
12 6.067
16 -2.269
20 -8.401
Root is between 12 and 16

6. 6
Estimate Properties of Roots By Graphical Methods
From (a) and (c):
if both f(xl) and f(xu) have the same sign, there must be 0 or even number of roots
From (b) and (d):
if f(xl) and f(xu) have different signs, there must be 1 or odd number of roots
Exceptions:
multiple roots
f(x) = (x-2)2(x-4)
discontinuous f(x)

7. 7
Find x such that f(x) = 0:
Step 1: Choose lower xl and upper xu such that f(xl)f(xu) < 0
Step 2: an estimate of the root
Step 3: Make the evaluations to determine in which interval the root lies:
(a) if f(xl)f(xr) < 0, the root lies in the lower interval; set xu = xr and
return to Step 2.
(b) if f(xl)f(xr) > 0, the root lies in the upper interval; set xl = xr and
return to Step 2.
(c) if f(xl)f(xr) = 0, the root = xr, stop.
Bisection Method
2
ul
r
xx
x



8. 8
s
t
rt
t
x
xx
 

 %100
||
||
snew
r
old
r
new
r
a
x
xx
 

 %
||
||
100
Error Estimates
But, we don’t know xt !
As an alternative, use:
true relative error εt, approximate relative error εa,
and acceptable error εs

9. 9
Example 1

10. 10

11. 11
Example 2

12. 12
f(x) = sin x – x3

13. 13

14. 14
Conservative Overestimate by a
a is always larger than t !
a
t

15. 15
Bisection Method
Pros
• Easy
• Always finds a root
• Number of iterations
required to attain an
absolute error.
Cons
• Slow
• Need to find initial
guesses for xl and xu
• No account is taken
of the fact that if f(xl)
is closer to zero, it is
likely that root is
closer to xl .

16. 16

17. 17
Incremental Search and Determining Initial Guesses
• For every interval xi – xi+1, apply bisection or false-
position method to find the roots in the interval
• Only roots in x4-x5 will be found