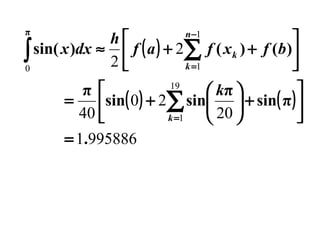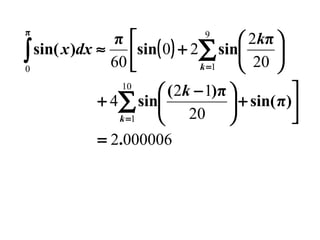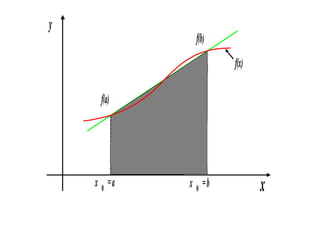
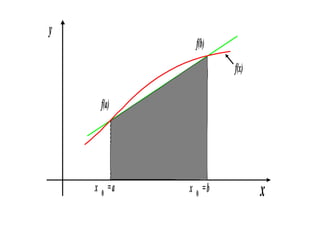
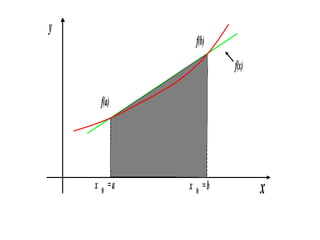
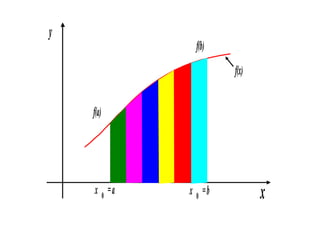
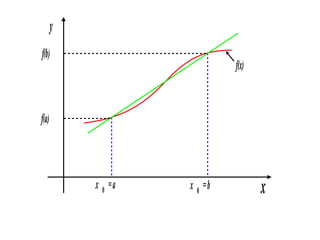
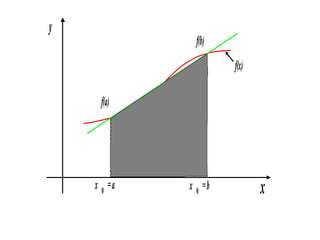
There are several numerical methods described for approximating derivatives and integrals: 1) Forward difference formula approximates the derivative as the slope of the secant line through two nearby points. 2) Three-point formulas approximate the derivative using the slopes of secant lines through three evenly spaced points, reducing the error term to O(h^2). 3) Trapezoidal rule approximates the integral of a function as the area of trapezoids formed between the function graph and the x-axis at evenly spaced points, with error term O(h^2).

2. NUMERICAL DIFFERENTIATION
The derivative of f (x) at x0 is:
f ′( x 0 ) =
Limit
h→ 0
f ( x0 + h) − f ( x0 )
h
An approximation to this is:
f ( x0 + h) − f ( x0 )
f ′( x 0 ) ≈
h
for small values of h.
Forward Difference
Formula

3. Let f ( x ) = ln x and x0 = 1.8
Find an approximate value for f ′(1.8)
h
f (1.8)
f (1.8 + h)
0.1 0.5877867 0.6418539
f (1.8 + h) − f (1.8)
h
0.5406720
0.01 0.5877867 0.5933268
0.5540100
0.001 0.5877867 0.5883421
0.5554000
The exact value of
f ′(1.8) = 0.55 5

4. Assume that a function goes through three points:
( x0 , f ( x0 ) ) , ( x1 , f ( x1 ) ) and ( x2 , f ( x2 ) ) .
f ( x) ≈ P( x)
P ( x ) = L0 ( x ) f ( x0 ) + L1 ( x ) f ( x1 ) + L2 ( x ) f ( x2 )
Lagrange Interpolating Polynomial

5. P ( x ) = L0 ( x ) f ( x0 ) + L1 ( x ) f ( x1 ) + L2 ( x ) f ( x 2 )
( x − x1 )( x − x2 )
P( x) =
f ( x0 )
( x0 − x1 )( x0 − x2 )
( x − x0 )( x − x2 )
+
f ( x1 )
( x1 − x0 )( x1 − x2 )
( x − x0 )( x − x1 )
+
f ( x2 )
( x2 − x0 )( x2 − x1 )

6. f ′( x ) ≈ P ′( x )
2 x − x1 − x2
P ′( x ) =
f ( x0 )
( x0 − x1 )( x0 − x2 )
2 x − x0 − x2
+
f ( x1 )
( x1 − x0 )( x1 − x2 )
2 x − x0 − x1
+
f ( x2 )
( x2 − x0 )( x2 − x1 )

7. If the points are equally spaced, i.e.,
x1 = x0 + h and x 2 = x0 + 2h
2 x0 − ( x0 + h) − ( x0 + 2h)
P ′( x0 ) =
f ( x0 )
{ x0 − ( x0 + h)}{ x0 − ( x0 + 2h)}
2 x0 − x0 − ( x0 + 2h)
+
f ( x1 )
{ ( x0 + h) − x0 }{ ( x0 + h) − ( x0 + 2h)}
2 x0 − x0 − ( x0 + h)
+
f ( x2 )
{ ( x0 + 2h) − x0 }{ ( x0 + 2h) − ( x0 + h)}

8. − 3h
− 2h
−h
P ′( x 0 ) =
f ( x0 ) +
f ( x1 ) + 2 f ( x 2 )
2
2
2h
−h
2h
1
{ − 3 f ( x0 ) + 4 f ( x1 ) − f ( x2 ) }
P ′( x0 ) =
2h
Three-point formula:
1
{ − 3 f ( x0 ) + 4 f ( x0 + h) − f ( x0 + 2h) }
f ′( x0 ) ≈
2h

9. If the points are equally spaced with x0 in the middle:
x1 = x0 − h and x 2 = x0 + h
2 x0 − ( x0 − h) − ( x0 + h)
P ′( x0 ) =
f ( x0 )
{ x0 − ( x0 − h)}{ ( x0 − ( x0 + h)}
2 x0 − x0 − ( x0 + h)
+
f ( x1 )
{ ( x0 − h) − x0 }{ ( x0 − h) − ( x0 + h)}
2 x0 − x0 − ( x0 − h)
+
f ( x2 )
{ ( x0 + h) − x0 }{ ( x0 + h) − ( x0 − h)}

10. 0
−h
h
P ′( x 0 ) =
f ( x0 ) + 2 f ( x1 ) + 2 f ( x 2 )
2
−h
2h
2h
Another Three-point formula:
1
{ f ( x0 + h) − f ( x0 − h) }
f ′( x0 ) ≈
2h

11. Alternate approach (Error estimate)
Take Taylor series expansion of f(x+h) about x:
2
3
h ( 2)
h ( 3)
f ( x + h) = f ( x ) + hf ′( x ) +
f ( x) +
f ( x) + 
2
3!
h2 ( 2 )
h3 ( 3 )
f ( x + h) − f ( x ) = hf ′( x ) +
f ( x) +
f ( x) + 
2
3!
f ( x + h) − f ( x )
h ( 2)
h2 ( 3 )
= f ′( x ) + f ( x ) +
f ( x) + 
h
2
3!
.............. (1)

12. f ( x + h) − f ( x )
= f ′( x ) + O ( h)
h
f ( x + h) − f ( x )
f ′( x ) =
− O ( h)
h
f ( x + h) − f ( x )
f ′( x ) ≈
h
Forward Difference
Formula
h ( 2)
h2 ( 3 )
O ( h) = f ( x ) +
f ( x) +
2
3!

13. 4h 2 ( 2 )
8h 3 ( 3 )
f ( x + 2h) = f ( x ) + 2hf ′( x ) +
f ( x) +
f ( x) + 
2
3!
4h 2 ( 2 )
8h 3 ( 3 )
f ( x + 2h) − f ( x ) = 2hf ′( x ) +
f ( x) +
f ( x) + 
2
3!
f ( x + 2h ) − f ( x )
2h ( 2 )
4h 2 ( 3 )
= f ′( x ) +
f ( x) +
f ( x) + 
2h
2
3!
................. (2)

14. f ( x + h) − f ( x )
h ( 2)
h ( 3)
= f ′( x ) + f ( x ) +
f ( x) + 
h
2
3!
.............. (1)
2
f ( x + 2h ) − f ( x )
2h ( 2 )
4h 2 ( 3 )
= f ′( x ) +
f ( x) +
f ( x) + 
2h
2
3!
................. (2)
2 X Eqn. (1) – Eqn. (2)

15. f ( x + h) − f ( x ) f ( x + 2h) − f ( x )
2
−
h
2h
2 h2 ( 3 )
6 h3 ( 4 )
= f ′( x ) −
f ( x) −
f ( x) − 
3!
4!
− f ( x + 2 h) + 4 f ( x + h) − 3 f ( x )
2h
2
3
2h ( 3 )
6h ( 4 )
′( x ) −
= f
f ( x) −
f ( x) − 
3!
4!
= f ′ ( x ) + O h2
( )

16. − f ( x + 2h ) + 4 f ( x + h ) − 3 f ( x )
= f ′( x ) + O h2
2h
( )
− f ( x + 2h ) + 4 f ( x + h ) − 3 f ( x )
f ′( x ) =
− O h2
2h
( )
− f ( x + 2h ) + 4 f ( x + h ) − 3 f ( x )
f ′( x ) ≈
2h
Three-point Formula
( )
2 h2 ( 3 )
6 h3 ( 4 )
O h2 = −
f ( x) −
f ( x) − 
3!
4!

17. The Second Three-point Formula
Take Taylor series expansion of f(x+h) about x:
h2 ( 2 )
h3 ( 3 )
f ( x + h) = f ( x ) + hf ′( x ) +
f ( x) +
f ( x) +
2
3!
Take Taylor series expansion of f(x-h) about x:
2
3
h ( 2)
h ( 3)
f ( x − h) = f ( x ) − hf ′( x ) +
f ( x) −
f ( x) + 
2
3!
Subtract one expression from another
2h 3 ( 3 )
2h 6 ( 6 )
f ( x + h) − f ( x − h) = 2hf ′( x ) +
f ( x) +
f ( x) + 
3!
6!

18. 2h 3 ( 3 )
2h 6 ( 6 )
f ( x + h) − f ( x − h) = 2hf ′( x ) +
f ( x) +
f ( x) + 
3!
6!
f ( x + h) − f ( x − h)
h2 ( 3)
h5 ( 6 )
= f ′( x ) +
f ( x) +
f ( x) + 
2h
3!
6!
f ( x + h) − f ( x − h) h 2 ( 3 )
h5 ( 6 )
f ′( x ) =
−
f ( x) −
f ( x) − 
2h
3!
6!

19. f ′( x ) =
f ( x + h ) − f ( x − h)
+ O h2
2h
( )
( )
h2 ( 3)
h5 ( 6 )
O h2 = −
f ( x) −
f ( x) − 
3!
6!
f ( x + h) − f ( x − h )
f ′( x ) ≈
2h
Second Three-point Formula

20. Summary of Errors
f ( x + h) − f ( x )
f ′( x ) ≈
h
Error term
Forward Difference
Formula
h ( 2)
h2 ( 3 )
O ( h) = f ( x ) +
f ( x) +
2
3!

21. Summary of Errors continued
First Three-point Formula
− f ( x + 2h ) + 4 f ( x + h ) − 3 f ( x )
f ′( x ) ≈
2h
( )
2 h2 ( 3 )
6 h3 ( 4 )
Error term O h2 = −
f ( x) −
f ( x) − 
3!
4!

22. Summary of Errors continued
Second Three-point Formula
f ( x + h) − f ( x − h )
f ′( x ) ≈
2h
( )
h2 ( 3)
h5 ( 6 )
O h2 = −
f ( x) −
f ( x) − 
Error term
3!
6!

23. Example:
f ( x ) = xe
x
Find the approximate value of
x
f ( x)
1.9
12.703199
2.0
14.778112
2.1
2.2
17.148957
19.855030
f ′( 2 )
with
h = 0.1

24. Using the Forward Difference formula:
1
f ′ ( x0 ) ≈ { f ( x0 + h ) − f ( x0 ) }
h
1
f ′ ( 2) ≈
{ f ( 2.1) − f ( 2 ) }
0.1
1
=
{ 17.148957 − 14.778112}
0.1
= 23.708450

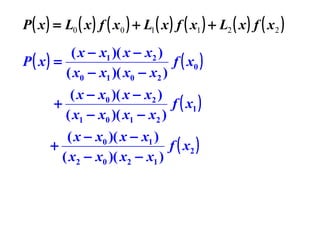
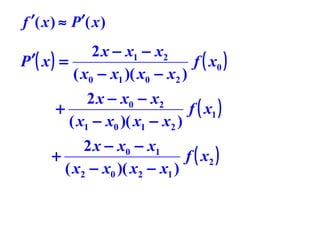
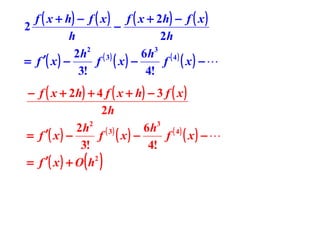
25. Using the 1st Three-point formula:
1
{ − 3 f ( x0 ) + 4 f ( x0 + h) − f ( x0 + 2h) }
f ′( x0 ) ≈
2h
1
[ − 3 f ( 2) + 4 f ( 2.1) − f ( 2.2)]
f ′( 2 ) ≈
2 × 0.1
1
[ − 3 × 14.778112 + 4 × 17.148957
=
0.2
− 19.855030 ]
= 22.032310

26. Using the 2nd Three-point formula:
1
{ f ( x0 + h) − f ( x0 − h) }
f ′( x0 ) ≈
2h
1
[ f ( 2.1) − f (1.9)]
f ′( 2 ) ≈
2 × 0.1
1
[ 17.148957 − 12.703199
=
0.2
= 22.228790
The exact value of
f ′( 2 ) is : 22.167168
]

27. Comparison of the results with h = 0.1
The exact value of f ′ ( 2 ) is 22.167168
Formula
f ′ ( 2)
Error
Forward Difference
23.708450
1.541282
1st Three-point
22.032310
0.134858
2nd Three-point
22.228790
0.061622

28. Second-order Derivative
h2 ( 2 )
h3 ( 3 )
f ( x + h) = f ( x ) + hf ′( x ) +
f ( x) +
f ( x) + 
2
3!
2
3
h ( 2)
h ( 3)
f ( x − h) = f ( x ) − hf ′( x ) +
f ( x) −
f ( x) + 
2
3!
Add these two equations.
2h 2 ( 2 )
2h4 ( 4 )
f ( x + h) + f ( x − h) = 2 f ( x ) +
f ( x) +
f ( x) + 
2
4!
2h2 ( 2 )
2 h4 ( 4 )
f ( x + h) − 2 f ( x ) + f ( x − h) =
f ( x) +
f ( x) +
2
4!

29. f ( x + h) − 2 f ( x ) + f ( x − h)
2h ( 4 )
( 2)
= f ( x) +
f ( x) + 
2
h
4!
2
f ( x + h ) − 2 f ( x ) + f ( x − h ) 2h 2 ( 4 )
f ( 2) ( x ) =
−
f ( x) + 
2
h
4!
f
( 2)
f ( x + h) − 2 f ( x ) + f ( x − h)
( x) ≈
h2

30. NUMERICAL INTEGRATION
b
∫ f ( x )dx =
a
area under the curve f(x) between
x = a to x = b.
In many cases a mathematical expression for f(x) is
unknown and in some cases even if f(x) is known its
complex form makes it difficult to perform the integration.

31. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

32. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

33. Area of the trapezoid
The length of the two parallel sides of the trapezoid
are: f(a) and f(b)
The height is b-a
b
∫
a
b−a
[ f ( a ) + f ( b )]
f ( x )dx ≈
2
h
= [ f ( a ) + f ( b )]
2

34. Simpson’s Rule:
∫
x2
x0
x2
f ( x )dx ≈ ∫ P ( x )dx
x0
x1 = x0 + h and x 2 = x0 + 2h

35. ∫
x2
x0
P ( x ) dx =
∫
+
∫
+
x2
x0
x2
x0
∫
x2
x0
( x − x1 )( x − x2 )
f ( x0 ) dx
( x0 − x1 )( x0 − x2 )
( x − x0 )( x − x2 )
f ( x1 ) dx
( x1 − x0 )( x1 − x2 )
( x − x0 )( x − x1 )
f ( x2 ) dx
( x2 − x0 )( x2 − x1 )

36. ∫
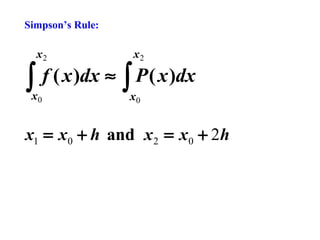
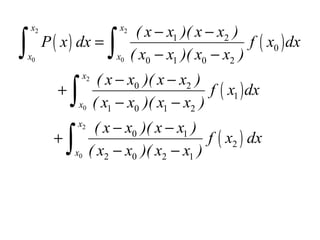
x2
x0
x2
f ( x )dx ≈ ∫ P ( x )dx
x0
h
= [ f ( x0 ) + 4 f ( x1 ) + f ( x 2 )]
3

37. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

38. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

39. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

40. y
f(b)
f(x)
f(a)
x 0 =a
x 0 =b
x

41. Composite Numerical Integration

42. Riemann Sum
The area under the curve is subdivided into n
subintervals. Each subinterval is treated as a
rectangle. The area of all subintervals are added
to determine the area under the curve.
There are several variations of Riemann sum as
applied to composite integration.

43. ∆ xIn Left Riemann
= ( b − a) / n
sum,
x1 = a the left-
x2
x3
side sample of
= afunction is
the + ∆ x
used as the
= a + 2∆the
x
height of
individual
M
rectangle.
xi = a + ( i − 1) ∆ x
∫
b
a
n
f ( x ) dx ≈ ∑ f ( xi ) ∆ x
i =1

44. ∆x = ( b − a) / n
In Right Riemann
sum, the right-side
x1 = a + ∆ x
sample of the
x2 = a is used
function+ 2∆ x as
the height of the
x3 = a + 3∆ x
individual rectangle.
M
xi = a + i∆ x
n
∫ f ( x ) dx ≈ ∑ f ( x ) ∆ x
b
a
i =1
i

45. In the ) / n
∆ x = ( b − aMidpoint
Rule, the sample at
x1 = the (middle1of ∆ x / 2 )
a + 2 ×1 − ) ( the
x2 =subinterval1is( used 2 )
a + ( 2× 2 − ) ∆x /
as the height of the
x3 = individual 1) ( ∆ x / 2 )
a + ( 2×3−
M rectangle.
xi = a + ( 2 × i − 1) ( ∆ x / 2 )
n
∫ f ( x ) dx ≈ ∑ f ( x ) ∆ x
b
a
i =1
i

46. Composite Trapezoidal Rule:
Divide the interval into n subintervals and apply
Trapezoidal Rule in each subinterval.
b
∫
a

h
f ( x )dx ≈  f ( a ) + 2∑ f ( x k ) + f (b )
2
k =1

n −1
where
b−a
h=
and x k = a + kh for k = 0, 1, 2, ... , n
n

47. π
Find
∫ sin (x)dx
0
by dividing the interval into 20 subintervals.
n = 20
b−a π
h=
=
n
20
kπ
x k = a + kh =
, k = 0, 1, 2, ....., 20
20

48. π

h
∫ sin( x )dx ≈ 2  f ( a ) + 2∑ f ( xk ) + f (b)
k =1


0
n −1
19

π 
 kπ 
=
sin( 0 ) + 2∑ sin 20  + sin( π ) 
40 
 
k =1

= 1.995886

49. Composite Simpson’s Rule:
Divide the interval into n subintervals and apply
Simpson’s Rule on each consecutive pair of subinterval.
Note that n must be even.
b
∫
a
h
f ( x )dx ≈  f ( a ) + 2
3
n/ 2
+ 4∑
k =1
( n / 2 ) −1
∑ f (x
k =1
2k
)

f ( x 2 k −1 ) + f (b )


50. where
b−a
h=
and x k = a + kh for k = 0, 1, 2, ... , n
n
π
Find
∫ sin (x)dx
0
by dividing the interval into 20 subintervals.
b−a π
n = 20
h=
=
n
20
kπ
x k = a + kh =
, k = 0, 1, 2, ....., 20
20

51. π
9
π 
 2kπ 
∫ sin( x )dx ≈ 60 sin( 0) + 2∑ sin 20 


k =1

0

 ( 2k − 1)π 
+ 4∑ sin
 + sin( π)
20 

k =1

= 2.000006
10