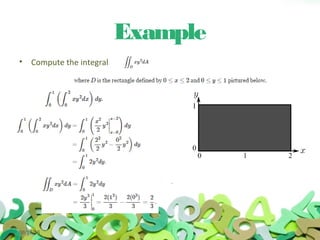
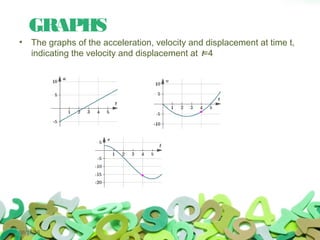
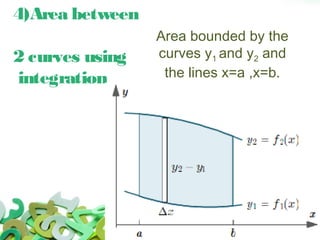
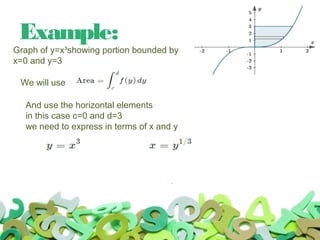
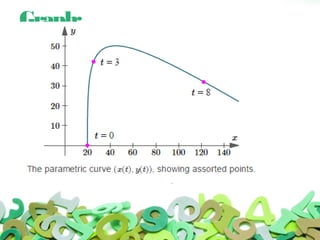
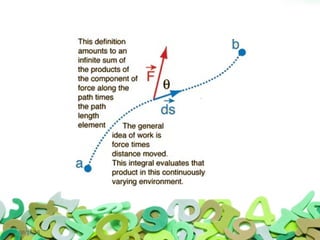
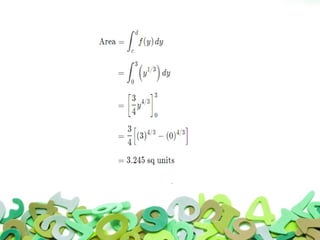This document discusses multivariable integrals and their applications. Multivariable integrals generalize single-variable integrals to functions with more than one variable, such as double integrals for two variables and triple integrals for three variables. These can be used to find the volume under a 3D surface. Examples are given of calculating mass and center of mass for 2D objects using double integrals of the density function over a region. Arc length of curves and work done by variable forces can also be determined using integrals.

1. MULTIVARIABLE
INTEGRALS
(JM)

2. Introduction
• The multivariable integral is the definite
integral of functions of more than one real
variable, for example, f(x, y) or f(x, y, z).
Integrals of a function of two variables over a
region are called double integrals, and
integrals of a function of three variables over
a region are called triple integrals.

3. 06/17/16
Interpretation
• A single variable integral is the area under the curve. So, the
multivariable integral can be interpretated as volume under a 3D curve.
• Consider a single variabled definite integral
• This is the area under the
curve f(x) from x=a to x=b.

4. 06/17/16
Interpretation
• The definite integral can be extended to functions of more than one
variable. Consider a function of 2 variables z=f(x,y). The definite integral is
denoted by
• where R is the region of
integration in the xy-plane.
• Here the curve is the graph
of the function
z=f(x,y). Then, the integral
gives the volume
of the space underneath it.

5. 06/17/16
Calculation
• A multivariable integral is calculated as an ilterated integral.
• This is similar to how we can compute partial derivatives by using our one-
variable differentiation rules. The trick in computing partial derivatives
was treating all the other variables as constant. we use a similar trick to
compute iterated integrals.
• First we integrate wrt x and treat y as constant and then vise versa. The
process can be extended to how ever many variables the function
depends upon.

6. 06/17/16
Example
• Compute the integral

7. 06/17/16
APPLICATIONS

8. 06/17/16
1)Mass of 2Dobject
• We can calculate the mass of a 2 dimensional object using double
integral if we know the function of its density.
• Let ρ(x,y) be the density of a lamina (flat sheet) R at the point (x,y).
ρ(x,y)=lim∆m /∆A
• where ∆m and ∆A are the mass and area of a small rectangle that
contains (x,y)
• Therefore we arrive at the definition of total mass in the lamina. All one
has to do is find the double integral of the density function.

9. 06/17/16
Example
• Let there is a thin metal plate that covers the
triangular region shown below. If the density
in the plate is measured by
ρ(x,y)=10-4x-2y
• Let the diagram shows the region the object covers.
• Mass
So, mass is 25/3 units

10. 06/17/16
2)Centerof mass in 2D
• Many structures and mechanical systems behave as if their masses were
concentrated at at single point, called the centre of mass. It is important to
locate this point so that we can better understand the behavior of our
structure or system.
• Formula for center of mass is:
• Here M is the mass given by
• And Mx and My are given by

11. 06/17/16
Example
• Let we have to calculate the center of gravity of an object whose density is
given by:
• we know mass of the object will be:
• we have
• These evaluate to:
Mx=5k/12 , My=5k/12
• Putting all these values in formula we get the center of
gravity as:
(x,y)=(5/8,5/8)
This tells us that the metal plate will balance perfectly if we place a pin at
(5/8,5/8)

12. 3)Indefinite Integral
Displacement fromVelocity, and Velocity from
Acceleration
• We can find an expression for velocity of a moving car by differentiating
the expression for displacement:
• Similarly, we can find the expression for the acceleration by
differentiating the expression for velocity, and this is equivalent to finding
the second derivative of the displacement:
06/17/16

13. 06/17/16
• It follows (since integration is the opposite process to
differentiation) that to obtain the displacement, s of an object at
time t (given the expression for velocity, we would use:
• Similarly, the velocity of an object at time t with acceleration a, is
given by:

14. • A car starts from rest at s=3 m from the origin and has acceleration
at time t given by a=2t−5 ms​−². Find the velocity and displacement
of the car at t=4 s.
06/17/16
EXAMPLE

15. GRAPHS
• The graphs of the acceleration, velocity and displacement at time t,
indicating the velocity and displacement at t=4
06/17/16

16. 4)Area between
2 curves using
integration
Area bounded by the
curves y1 and y2 and
the lines x=a ,x=b.

17. • Curved surfaces are very common in our everyday life. Let there is a
bridge whose pillars are curved and we need to find the area
between two curved pillars in order to determine weather a car will be
able to pass through or not.
• Then lets say the two curves are given by:
• We see that if we subtract the area under lower curve
from the area under upper curve
We get required area.
• This can be achieved in one step easily if we use integration like so:

18. Example:
Graph of y=x³showing portion bounded by
x=0 and y=3
We will use
And use the horizontal elements
in this case c=0 and d=3
we need to express in terms of x and y

20. 5)Arc Length Of Curve:
Parametric:
• We can find the length of an arc by using integrals.
•This application is useful in situations that involve curved paths e.g
race car tracks

21. Example
Example - Race Track
A race car was travelling around a curve described in parametric
equations as:
x(t)=20+0.2t³
y(t)=20t-2t²
where x and y are in meters and t is time in seconds.
What is the distance travelled by the car in the first 8 seconds?

22. Solution:

23. Graph:

24. length=144.7 m.

25. 06/17/16
7)WorkDone
• The work (W) done by a constant force (F) acting on a body
by moving it through a distance (d) is given by:
W = F × d
• The general definition of work done by a force must take into
account the fact that the force may vary in both magnitude and
direction, and that the path followed may also change in
direction. All these things can be taken into account by
defining work as an integral.

26. 06/17/16

27. 06/17/16

28. CONCLUSION
• Integrals have many real life applications.
• We can find masses of 2 dimensional objects like a sheet of metal.
• We can also find the center of mass of an object like a disc.
• Acceleration and velocity of moving objects like cars can also be found
using integrals.
• The arc length of a curve like a portion of race car track can also be
found using integrals.
• Work done by a variable force or in a variable direction can be found
using integrals.
06/17/16