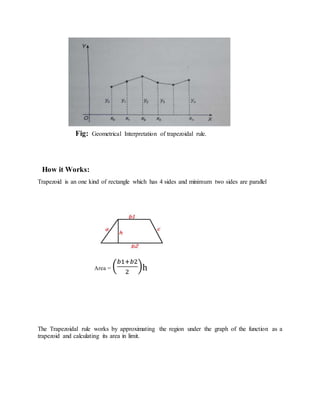
The document defines the trapezoidal rule for approximating definite integrals. It provides the trapezoidal formula, explains the geometric interpretation of dividing the region into trapezoids, and outlines an algorithm and flowchart for implementing the trapezoidal rule in Python. Sample problems applying the trapezoidal rule are included to evaluate definite integrals numerically.

1. Problem Statement: Define trapezoidal formula for, write the algorithm, draw the
flowchart, and develop a python program for trapezoidal formula.
Trapezoidal Formula:
In Numerical analysis, the trapezoidal rule or method is a technique for approximating the
definite integral.
∫ 𝑓( 𝑥) 𝑑𝑥
𝑥𝑛
𝑥0
= h 1.y0 +
1
2
∆𝑦0
It is also known as trapezium rule.
In general Integration formula when n=1 its trapezoidal rule is
= h 1.y0 +
1
2
(𝑦1 − 𝑦0
= h/2 (y0 + y1)
∫ 𝑓( 𝑥) 𝑑𝑥
𝑥n
𝑥0
= ∫ 𝑓( 𝑥) 𝑑𝑥
𝑥0+𝑛ℎ
𝑥0
= ∫ 𝑓( 𝑥) 𝑑𝑥
𝑥0+ℎ
𝑥0
+ ∫ 𝑓( 𝑥) 𝑑𝑥 + ⋯.
𝑥0+2ℎ
𝑥0+ℎ
+ ∫ 𝑓( 𝑥) 𝑑𝑥
𝑥0+𝑛ℎ
𝑥0+( 𝑛−1)ℎ
=
ℎ
2
(y0+ y1) +
ℎ
2
(y1+y2) + …….. + h/2 (yn-1 + yn)
=
ℎ
2
(y0+ y1) + 2(y1+y2+ y3+ y4+…….. yn-1)
= h/2 sum of the first and last ordinates + 2(sum of the remaining ordinates)
Geometrical Interpretation:
Geometrically, if the ordered pairs (x1, y1), i = 0, 1, 2,…….,n are potted, and if any two
consecutive points are joined by straight lines, we get the figure as shown.
The area between f(x), x-axis and ordinates x = x0 and x = xn is approximated to sum of the
areas of the trapeziums as shown in the figure.

2. Fig: Geometrical Interpretation of trapezoidal rule.
How it Works:
Trapezoid is an one kind of rectangle which has 4 sides and minimum two sides are parallel
Area = (
𝑏1+𝑏2
2
)h
The Trapezoidal rule works by approximating the region under the graph of the function as a
trapezoid and calculating its area in limit.

3. It follows that,
∫ 𝑓( 𝑥) 𝑑𝑥 ≈ (
𝑏 − 𝑎
2
)[ 𝑓( 𝑎) + 𝑓(𝑏)]
𝑏
𝑎
The Trapezoidal rule approximation improves with more strips, from this figure we can clearly see
it
Truncation error in Trapezoidal rule:
In the neighbourhood of x = x0, we can expand y = f(x), by Tailor series in power of x-x0, that
is,
Y(x) = y0 +
(𝑥−𝑥0)
1!
(y0’) +
(𝑥−𝑥0)2
2!
(y0”) + …… + …

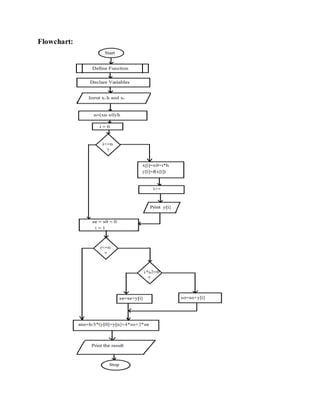
4. Algorithm:
 Start
 Define and Declare the function
 Input initial boundary value, final boundary value and length of interval
 Calculate number of strips, n=(final boundary value-initial boundary value)/length of
interval
 Perform the following operations in loop
x[i]=x0+i*h
y[i]=f(x[i])
print y[i]
 Initialize se=0,s0=0
 Do the following using a loop
if i%2=0
s0=s0+y[i]
Otherwise
se=se+y[i]
 ans=h/3*(y[0]+y[n]+4*s0+2*se
 print the ans
 stop

5. Flowchart:

6. Coding:
def Trapezoidal(f, a, b, n):
h = (b-a)/float (n)
s = 0.5*(f (a) + f(b))
for i in range(1,n,1):
s = s + f(a + i*h)
return h*s
from math import exp
def g(t):
return exp(-t**4)
a = -2; b = 2
n = 1000
result = Trapezoidal(g, a, b, n)
print result
Sample Input:
Enter sample inputes
a = -2, b = 2, n= 1000
Sample Output:
Answer is: 1.8128049473666044
Exercise:
Problem 1: Evaluate ∫ 𝑑𝑥/
6
0
(1+x2) by using Trapezoidal rule.
Solution:
Divide the interval (0,6) into 6 parts each of width h = 1, The values of f(x)=
1
1+𝑥2
are given
below.

7. x 0 1 2 3 4 5 6
F(x)x = y 1 0.5 0.2 0.1 0.0588 0.0385 0.027
Y0 Y1 Y2 Y3 Y4 Y5 Y6
By Trapezoidal rule, we have,
∫
𝑑𝑥
(1+𝑥2)
6
0
=
ℎ
2
(y0+ y6) + 2(y1+y2+ y3+ y4 + y5)
=
ℎ
2
(1+0.027) + 2(0.5+0.2+0.1+0.0588+0.0385)
= 1.4108
The answer is 1.4108
Problem 2: Dividing the range into 10 equal ports, find the approximate value of ∫ 𝑠𝑖𝑛𝑥𝑑𝑥
𝜋
0
by trapezoidal rule.
Solution:
The range (0,𝜋) is divided into 10 equal parts,
Hence, h = 𝜋/10
We compute the values of sinx for each point of subdivision,
i.e., for x =0,
𝜋
10
,
2𝜋
10
, … … 𝜋. These values are tabulated as follows
x 0 𝜋/10 2𝜋/10 3𝜋/10 4𝜋/10 5𝜋/10 6𝜋/10 7𝜋/10 8𝜋/10 9𝜋/10 𝜋
sinx 0 0.3090 0.5878 0.8090 0.9511 1 0.9511 0.8090 0.5878 0.3090 0
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10
By Trapezoidal rule, we have,
∫ 𝑠𝑖𝑛𝑥𝑑𝑥
𝑥
0
=
ℎ
2
(y0+ y10) + 2(y1+y2+ y3+ y4 + y5+ y6+y7+ y8+ y9)
h =
𝜋
10
∫ 𝑠𝑖𝑛𝑥𝑑𝑥
𝑥
0
=
𝜋
20
(0+0) + 2(0.3090+0.5878+0.8090+0.9511+1+0.3090+0.5878+0.8090+0.9511)
=
𝜋
20
2*6.3138)
= 1.984 (approximately)
The answer is 1.984.

8. Problem 3: Using n=5, Calculate approximate the integral by trapezoidal rule.
∫ √
5
1
(x2+1).
Solution:
For n = 5 we have △x = 5−1/5= 0.8
Computing the values for y0, y1,......,y5
x y = √1+x2
1 1.41
1.8 2.06
2.6 2.78
3.4 3.54
4.2 4.32
5 5.10
∫ √
5
1
(x2+1) dx = 0.8/2 (1.41 + 2(2.06) + 2(2.18) + 2(3.54) + 2(4.32) + (5.10))
= 12.284
The answer is 12.284.
Conclusion:
The above program is successfully written in python programming language for Trapezoidal
formula which can calculate the approximating integrals.
Reference:
1. https://en.wikipedia.org/wiki/Trapezoidal_rule
2. https://stackoverflow.com