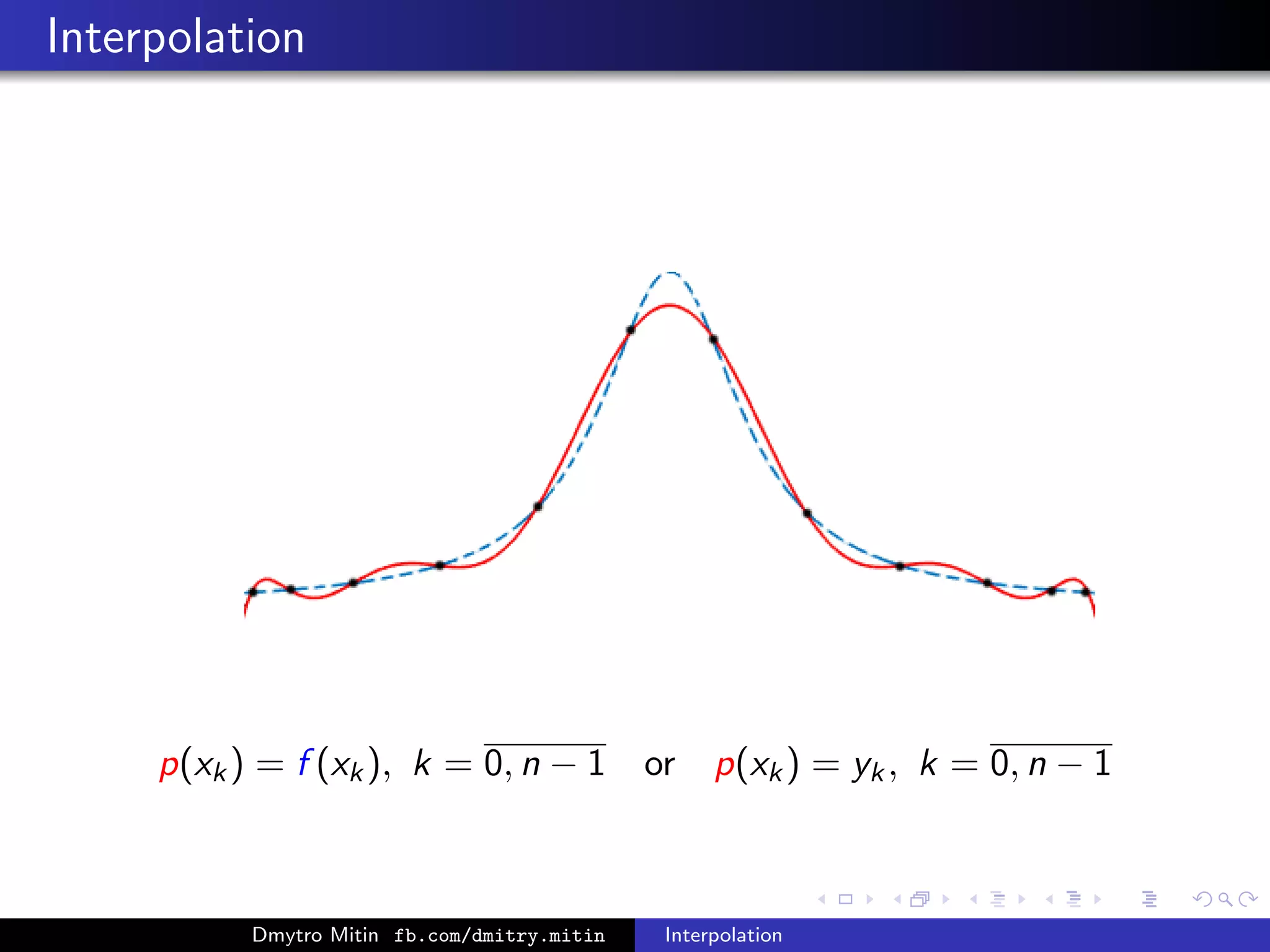
The document discusses various methods of interpolation, including Lagrange and Newton interpolation polynomials. Lagrange interpolation involves constructing a polynomial that passes through a set of n data points, represented by its values at the points. Newton interpolation similarly uses a polynomial but is based on divided differences. Both can be used to interpolate values within or extrapolate beyond the original data range. The complexity of calculating the interpolation polynomials is also addressed.

1. Interpolation
Dmytro Mitin
fb.com/dmitry.mitin
21 October 2015. Algoclub #17
Dmytro Mitin fb.com/dmitry.mitin Interpolation

2. Interpolation of functions
Finite differences
Divided differences
Lagrange interpolating polynomial
Newton interpolating polynomial
Hermite interpolating polynomial∗
Interpolation error
Neville algorithm
Algorithmic complexity of interpolation
Dmytro Mitin fb.com/dmitry.mitin Interpolation

3. String interpolation
int x = 5, y = 4;
System.out.println(String.format("%d * %d = %d",
x, y, x * y));
5 * 4 = 20
Dmytro Mitin fb.com/dmitry.mitin Interpolation

4. How many roots?
c ·
(x − a)(x − b)
(c − a)(c − b)
+ a ·
(x − b)(x − c)
(a − b)(a − c)
+ b ·
(x − c)(x − a)
(b − c)(b − a)
= x
(a, b, c are fixed, a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

5. How many roots?
(x − a)(x − b)
(c − a)(c − b)
+
(x − b)(x − c)
(a − b)(a − c)
+
(x − c)(x − a)
(b − c)(b − a)
= 1
(a, b, c are fixed, a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

6. How many roots?
c2
·
(x − a)(x − b)
(c − a)(c − b)
+a2
·
(x − b)(x − c)
(a − b)(a − c)
+b2
·
(x − c)(x − a)
(b − c)(b − a)
= x2
(a, b, c are fixed, a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

7. How many roots?
c3
·
(x − a)(x − b)
(c − a)(c − b)
+a3
·
(x − b)(x − c)
(a − b)(a − c)
+b3
·
(x − c)(x − a)
(b − c)(b − a)
= x3
(a, b, c are fixed, a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

8. How many roots?
c4
·
(x − a)(x − b)
(c − a)(c − b)
+a4
·
(x − b)(x − c)
(a − b)(a − c)
+b4
·
(x − c)(x − a)
(b − c)(b − a)
= x4
(a, b, c are fixed, a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

9. Extrapolation
World population
Dmytro Mitin fb.com/dmitry.mitin Interpolation

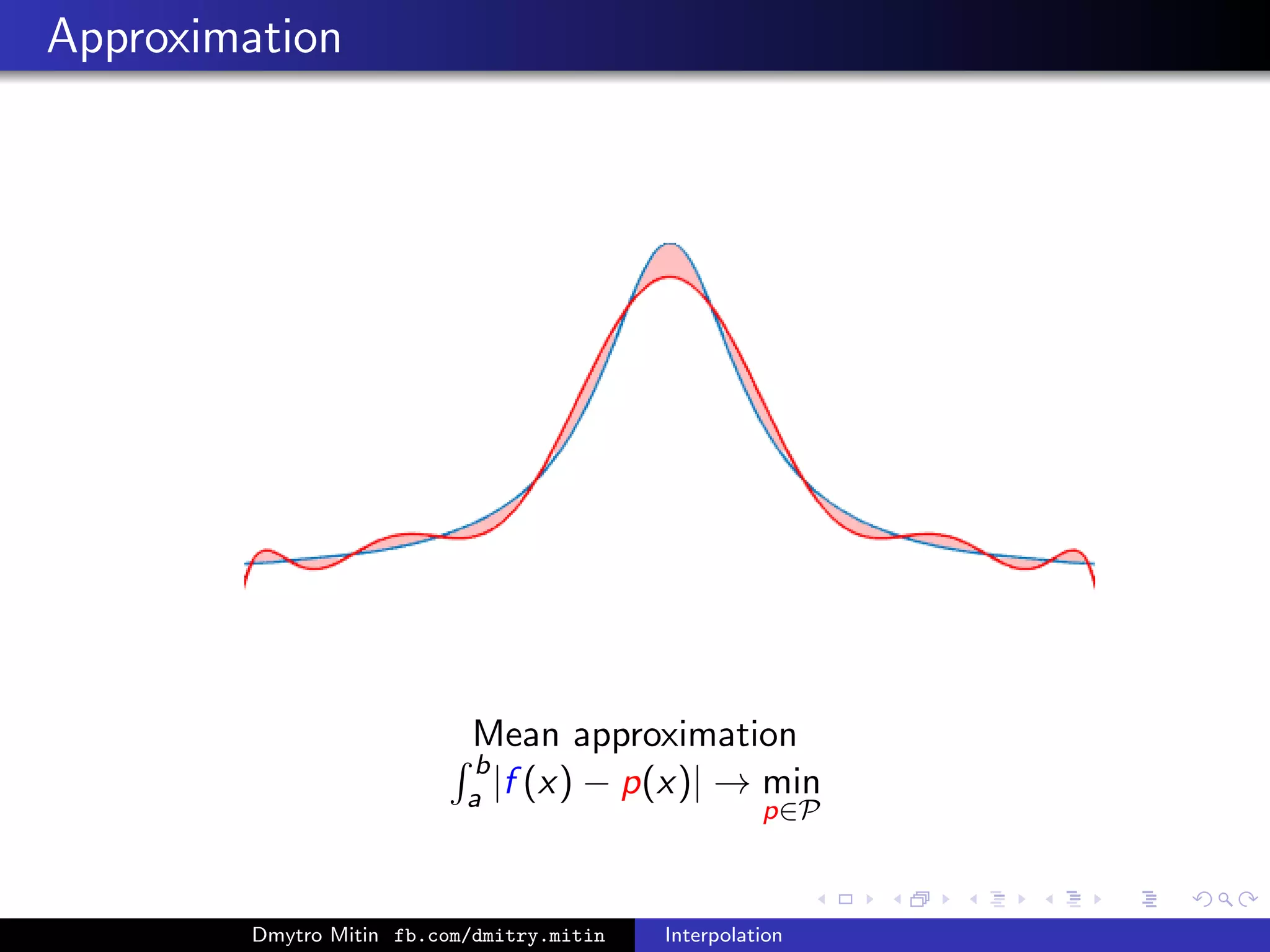
10. Approximation
Uniform approximation
max
x∈[a,b]
|f (x) − p(x)| → min
p∈P
Dmytro Mitin fb.com/dmitry.mitin Interpolation

11. Approximation
Mean approximation
b
a |f (x) − p(x)| → min
p∈P
Dmytro Mitin fb.com/dmitry.mitin Interpolation

12. Interpolation
p(xk) = f (xk), k = 0, n − 1 or p(xk) = yk, k = 0, n − 1
Dmytro Mitin fb.com/dmitry.mitin Interpolation

13. Lagrange interpolating polynomial
n = 3
p(x) = f (c)·
(x − a)(x − b)
(c − a)(c − b)
+f (a)·
(x − b)(x − c)
(a − b)(a − c)
+f (b)·
(x − c)(x − a)
(b − c)(b − a)
p(a) = f (a), p(b) = f (b), p(c) = f (c)
(a = b, b = c, c = a)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

14. Lagrange interpolating polynomial
p(x) = f (x0) ·
(x − x0)(x − x1) . . . (x − xn−1)
(x0 − x0)(x0 − x1) . . . (x0 − xn−1)
+ f (x1) ·
(x − x0)
(x − x1) . . . (x − xn−1)
(x1 − x0)
(x1 − x1) . . . (x1 − xn−1)
+ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
+ f (xn−1) ·
(x − x0)(x − x1) . . .
(x − xn−1)
(xn−1 − x0)(xn−1 − x1) . . .(((((((
(xn−1 − xn−1)
p(x0) = f (x0), p(x1) = f (x1), . . . , p(xn−1) = f (xn−1)
(x0 = . . . = xn−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

15. p(x) =
n−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xn−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xn−1)
Definition
Lagrange interpolating polynomial
p(x) =
n−1
k=0
f (xk) ·
0≤j≤n−1
j=k
(x − xj )
0≤j≤n−1
j=k
(xk − xj )
p(xk) = f (xk), k = 0, n − 1
(x0 = . . . = xn−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

16. Joseph-Louis Lagrange (1736–1813)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

17. Uniqueness
p(x) =
n−1
i=0
ai xi
p(xk) = f (xk), k = 0, n − 1
n−1
i=0
ai xi
k = f (xk), k = 0, n − 1
det
1 1 . . . 1
x0 x1 . . . xn−1
x2
0 x2
1 . . . x2
n−1
. . . . . . . . . . . .
xn−1
0 xn−1
1 . . . xn−1
n−1
=
0≤jk≤n−1
(xk − xj ) = 0,
x0 = . . . = xn−1
Dmytro Mitin fb.com/dmitry.mitin Interpolation

18. Equidistant nodes
p(x) =
n−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xn−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xn−1)
Partial case: x1 − x0 = x2 − x1 = . . . = xn−1 − xn−2 = h,
xk = x0 + k · h, k = 0, n − 1
p(x) =
n−1
k=0
f (x0 + k h) · (x−x0)(x−x0−h)...((((((x−x0−k·h)...(x−x0−(n−1)h)
k(k−1)...(k−k)...(k−n+1)·hn−1
p(x) =
n−1
k=0
f (x0 + k h) ·
t(t − 1) . . .(t − k) . . . (t − n + 1)
k!(n − k − 1)!(−1)n−k−1
,
t =
x − x0
h
Dmytro Mitin fb.com/dmitry.mitin Interpolation

19. Complexity
p(x) =
n−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xn−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xn−1)
What is complexity?
Is this formula good?
Dmytro Mitin fb.com/dmitry.mitin Interpolation

20. p(x) =
n−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xn−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xn−1)
≡ pn(x)
p(x) = p1(x) +
n−1
j=1
pj+1(x) − pj (x)
p(x) = f (x0) +
n−1
j=1
j
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xj )
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
−
j−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xj−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xj−1)
p(x) = f (x0) +
n−1
j=1
Cj · (x − x0)(x − x1) . . . (x − xj−1)
Attention! Algebraic trick:
x = x0, x1, . . . , xj−1
j
are zeroes, deg = j
Dmytro Mitin fb.com/dmitry.mitin Interpolation

21. Let’s rewrite formula
p(x) = f (x0) +
n−1
j=1
j
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xj )
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
−
j−1
k=0
f (xk) ·
(x − x0) . . .
(x − xk) . . . (x − xj−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xj−1)
p(x) = f (x0) +
n−1
j=1
Cj · (x − x0)(x − x1) . . . (x − xj−1)
Cj ? x = xj :
f (xj ) −
j−1
k=0
f (xk) ·
(xj − x0) . . .
(xj − xk) . . . (xj − xj−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xj−1)
= Cj · (xj − x0)(xj − x1) . . . (xj − xj−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

22. Let’s rewrite formula
f (xj ) −
j−1
k=0
f (xk) ·
(xj − x0) . . .
(xj − xk) . . . (xj − xj−1)
(xk − x0) . . .
(xk − xk) . . . (xk − xj−1)
= Cj · (xj − x0)(xj − x1) . . . (xj − xj−1)
Cj =
f (xj )
(xj − x0)(xj − x1) . . . (xj − xj−1)
−
j−1
k=0
f (xk) ·
1
(xk − x0) . . .
(xk − xk) . . . (xk − xj−1)
·
1
xj − xk
Cj =
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
Dmytro Mitin fb.com/dmitry.mitin Interpolation

23. Cj =
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
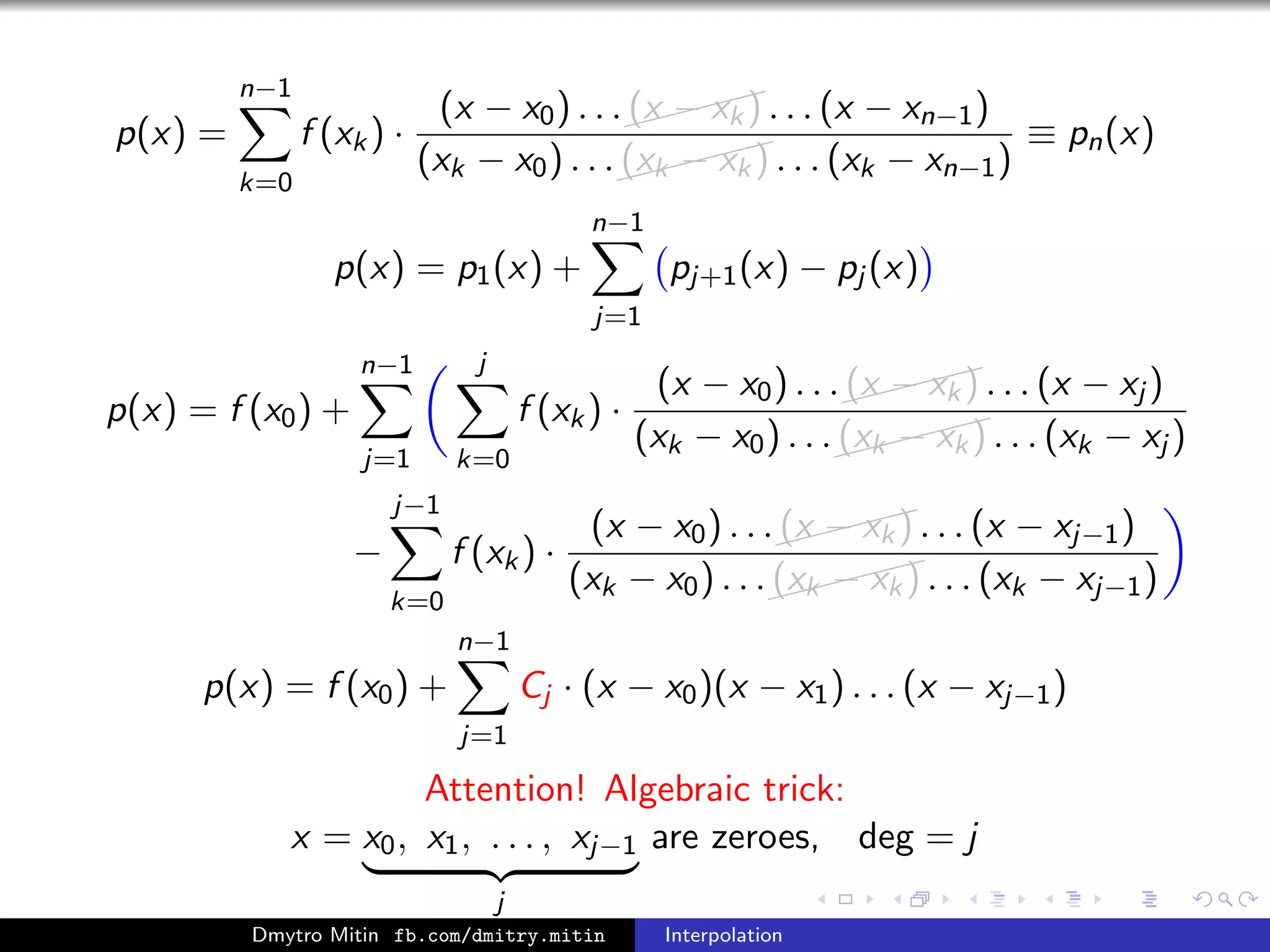
p(x) = f (x0) +
n−1
j=1
Cj · (x − x0)(x − x1) . . . (x − xj−1)
p(x) = f (x0) +
n−1
j=1
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
·(x − x0)(x − x1) . . . (x − xj−1)
Definition
Newton interpolating polynomial
p(x) = f (x0) +
n−1
j=1
[f ; x0, x1, . . . , xj ]
Divided differences
· (x − x0)(x − x1) . . . (x − xj−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

24. Isaac Newton (1643–1727)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

25. Equidistant nodes
p(x) =
n−1
j=0
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
·(x − x0)(x − x1) . . . (x − xj−1)
Partial case: x1 − x0 = x2 − x1 = . . . = xn−1 − xn−2 = h,
xk = x0 + k · h, k = 0, n − 1
p(x) =
n−1
j=0
j
k=0
f (x0 + k h)
k!(j − k)!(−1)j−khj
·(x − x0)(x − x0 − h) . . . (x − x0 − (j − 1)h)
p(x) =
n−1
j=0
1
j!
j
k=0
(−1)j−k
Ck
j f (x0 + k h) · t(t − 1) . . . (t − j + 1)
t = x−x0
h , Ck
j = j!
k!(j−k)!
Dmytro Mitin fb.com/dmitry.mitin Interpolation

26. Finite differences
p(x) =
n−1
j=0
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
·(x − x0)(x − x1) . . . (x − xj−1)
p(x) =
n−1
j=0
1
j!
j
k=0
(−1)j−k
Ck
j f (x0 + k h) · t(t − 1) . . . (t − j + 1)
t =
x − x0
h
, Ck
j =
j!
k!(j − k)!
∆j
f (x0, h) =
j
k=0
(−1)j−k
Ck
j f (x0 + k h)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

27. Finite differences
∆j
f (x0, h) =
j
k=0
(−1)j−k
Ck
j f (x0 + k h)
∆0
f (x0, h) = f (x0)
∆j
f (x0, h) = ∆(∆j−1
f )(x0, h)
∆f (x0, h) = f (x0 + h) − f (x0)
∆2
f (x0, h) = ∆(∆f )(x0, h) = ∆f (x0 + h) − ∆f (x0)
= f (x0 + 2h) − 2f (x0 + h) + f (x0)
∆3
f (x0, h) = f (x0 + 3h) − 3f (x0 + 2h) + 3f (x0 + h) − f (x0)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

28. Complexity
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
p(xk) = f (xk), k = 0, n − 1
[f ; x0, x1, . . . , xj ] =
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
How to add new node?
What is complexity?
Dmytro Mitin fb.com/dmitry.mitin Interpolation

29. Divided differences
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
[f ; x0, x1, . . . , xj ] =
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
[f ; x0] = f (x0)
[f ; x0, x1] =
f (x0)
x0 − x1
+
f (x1)
x1 − x0
=
f (x0) − f (x1)
x0 − x1
[f ; x0, x1, x2] = f (x0)
(x0−x1)(x0−x2) + f (x1)
(x1−x0)(x1−x2) + f (x2)
(x2−x0)(x2−x1)
=
f (x0)−f (x1)
x0−x1
− f (x1)−f (x2)
x1−x2
x0 − x2
=
[f ; x0, x1] − [f ; x1, x2]
x0 − x2
Dmytro Mitin fb.com/dmitry.mitin Interpolation

30. Divided differences
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
[f ; x0, x1, . . . , xj ] =
j
k=0
f (xk)
(xk − x0) . . .
(xk − xk) . . . (xk − xj )
Recurrence:
[f ; x0, x1, . . . , xj−1, xj ] =
[f ; x0, x1, . . . , xj−1] − [f ; x1, . . . , xj−1, xj ]
x0 − xj
, j ≥ 1
[f ; x0] = f (x0)
[f ; . . . , xr , . . . , xs, . . .] =
[f ; . . . , xr , . . . ,xs, . . .] − [f ; . . . ,xr , . . . , xs, . . .]
xr − xs
Dmytro Mitin fb.com/dmitry.mitin Interpolation

31. Interpolation error
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
p(xk) = f (xk), k = 0, n − 1
q(x) =
n
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
= p(x) + [f ; x0, x1, . . . , xn] · (x − x0)(x − x1) . . . (x − xn−1)
q(xk) = f (xk), k = 0, n
f (xn) = q(xn) = p(xn) + [f ; x0, x1, . . . , xn]
·(xn − x0)(xn − x1) . . . (xn − xn−1)
f (x) = p(x) + [f ; x0, x1, . . . , xn−1, x]
·(x − x0)(x − x1) . . . (x − xn−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

32. Interpolation error
f (x) = p(x) + [f ; x0, x1, . . . , xn−1, x]
·(x − x0)(x − x1) . . . (x − xn−1)
f (xk) − p(xk) = 0, k = 0, n − 1
f (n−1)
(ξ) − p(n−1)
(ξ) = 0, ξ ∈ [a, b] x0, . . . , xn−1
f (n−1)
(ξ) = p(n−1)
(ξ) = [f ; x0, x1, . . . , xn−1] · (n − 1)!
[f ; x0, x1, . . . , xn−1] =
f (n−1)(ξ)
(n − 1)!
f (x) − p(x) =
f (n−1)(ξ)
(n − 1)!
· (x − x0)(x − x1) . . . (x − xn−1)
|f (x) − p(x)| ≤
1
(n − 1)!
max
[a,b]
|f (n−1)
| · (b − a)n
, x ∈ [a, b]
Dmytro Mitin fb.com/dmitry.mitin Interpolation

33. Neville algorithm
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
= f (x0) + (x − x0) · [f ; x0, x1] + (x − x1) ·
. . . [f ; x0, . . . , xn−2] + (x − xn−1)[f ; x0, . . . , xn−1] . . .
[f ; x0, x1, . . . , xj−1, xj ] =
[f ; x0, x1, . . . , xj−1] − [f ; x1, . . . , xj−1, xj ]
x0 − xj
[f ; x0, . . . , xn−1]
[f ; x0, . . . , xn−2] [f ; x1, . . . , xn−1]
[f ; x0, . . . , xn−3] [f ; x1, . . . , xn−2] [f ; x2, . . . , xn−1]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[f ; x0, x1] [f ; x1, x2] [f ; x2, x3] . . . . . . [f ; xn−3, xn−2] [f ; xn−2, xn−1]
f (x0) f (x1) f (x2) f (x3) . . . f (xn−3) f (xn−2) f (xn−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

34. Eric Harold Neville (1889–1961)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

35. Neville algorithm
p(x) =
n−1
j=0
[f ; x0, x1, . . . , xj ] · (x − x0)(x − x1) . . . (x − xj−1)
[f ; x0, x1, . . . , xj−1, xj ] =
[f ; x0, x1, . . . , xj−1] − [f ; x1, . . . , xj−1, xj ]
x0 − xj
[f ; x0, x1, x2, . . . , xj ] =
[f ; x0, x2, . . . , xj ] − [f ; x1, x2, . . . , xj ]
x0 − x1
p(x) ≡ p(f ; x0, . . . , xn−1; x)
p(f ; x0, . . . , xn−1; x) = f (x0) +
f (x0) − f (x1)
x0 − x1
(x − x0)
+
x − x1
x0 − x1
n−1
j=2
[f ; x0, x2, . . . , xj ] · (x − x0)(x − x2) . . . (x − xj−1)
−
x − x0
x0 − x1
n−1
j=2
[f ; x1, . . . , xj ] · (x − x1) . . . (x − xj−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

36. Neville algorithm
p(f ; x0, . . . , xn−1; x) = f (x0) +
f (x0) − f (x1)
x0 − x1
(x − x0)
+
x − x1
x0 − x1
n−1
j=2
[f ; x0, x2, . . . , xj ] · (x − x0)(x − x2) . . . (x − xj−1)
−
x − x0
x0 − x1
n−1
j=2
[f ; x1, . . . , xj ] · (x − x1) . . . (x − xj−1)
p(f ; x0, . . . , xn−1; x) = f (x0) +
f (x0) − f (x1)
x0 − x1
(x − x0)
+
x − x1
x0 − x1
p(f ; x0, x2, . . . , xn−1; x) − f (x0)
−
x − x0
x0 − x1
p(f ; x1, . . . , xn−1; x) − f (x1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

37. Neville algorithm
p(f ; x0, . . . , xn−1; x) = f (x0) +
f (x0) − f (x1)
x0 − x1
(x − x0)
+
x − x1
x0 − x1
p(f ; x0, x2, . . . , xn−1; x) − f (x0)
−
x − x0
x0 − x1
p(f ; x1, . . . , xn−1; x) − f (x1)
p(f ; x0, . . . , xn−1; x) =
x − x1
x0 − x1
p(f ; x0, x2, . . . , xn−1; x)
+
x0 − x
x0 − x1
p(f ; x1, . . . , xn−1; x)
p(f ; x0, . . . , xn−1; x) =
x − xn−1
x0 − xn−1
p(f ; x0, . . . , xn−2; x)
+
x0 − x
x0 − xn−1
p(f ; x1, . . . , xn−1; x)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

38. Neville algorithm
Recurrence for interpolating polynomials
p(f ; x0, . . . , xn−1; x) =
x − xn−1
x0 − xn−1
p(f ; x0, . . . , xn−2; x)
+
x0 − x
x0 − xn−1
p(f ; x1, . . . , xn−1; x)
p(f ; x0, . . . , xn−1; x)
p(f ; x0, . . . , xn−2; x) p(f ; x1, . . . , xn−1; x)
p(f ; x0, . . . , xn−3; x) p(f ; x1, . . . , xn−2; x) p(f ; x2, . . . , xn−1; x)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p(f ; x0, x1; x) p(f ; x1, x2; x) . . . p(f ; xn−3, xn−2; x) p(f ; xn−2, xn−1; x)
f (x0) f (x1) f (x2) . . . f (xn−2) f (xn−1)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

39. Hermite interpolating polynomial
p(xk) = f (xk), p (xk) = f (xk), . . . , p(mk −1)
(xk) = f (mk −1)
(xk),
k = 0, n − 1
1
(x − x0)m0 . . .
(x − xk)mk . . . (x − xn−1)mn−1
=
∞
j=0
ckj (x − xk)j
= qki (x) +
∞
j=mk −i
ckj (x − xk)j
, deg qki ≤ mk − i − 1
p(x) =
n−1
k=0
(x − x0)m0
. . .
(x − xk)mk
. . . (x − xn−1)mn−1
·
mk −1
i=0
f (i)(xk)
i!
(x − xk)i
qki (x)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

40. Charles Hermite (1822–1901)
Dmytro Mitin fb.com/dmitry.mitin Interpolation

41. What’s next?
Nonpolynomial interpolation (rational functions, . . . )
Multivariate interpolation
Fractal interpolation
. . .
Dmytro Mitin fb.com/dmitry.mitin Interpolation

42. It’s coding time!
Problem 1.
Double interpolateAtPoint
(ListDouble nodes,
Double point,
UnaryOperatorDouble function){
// UnaryOperatorDouble function = x - x * x;
// code here
}
Problem 2.
void addNodeAndUpdateDividedDifferences
(ListDouble nodes,
Double newNode,
ListListDouble dividedDifferences,
UnaryOperatorDouble function) {
//code here
}
Dmytro Mitin fb.com/dmitry.mitin Interpolation

43. Links
https://en.wikipedia.org/wiki/Interpolation
https://en.wikipedia.org/wiki/Finite difference
https://en.wikipedia.org/wiki/Divided differences
https://en.wikipedia.org/wiki/Polynomial interpolation
https://en.wikipedia.org/wiki/Lagrange polynomial
https://en.wikipedia.org/wiki/Newton polynomial
https://en.wikipedia.org/wiki/Hermite interpolation
http://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html
http://mathworld.wolfram.com
/NewtonsDividedDifferenceInterpolationFormula.html
http://mathworld.wolfram.com/HermitesInterpolatingPolynomial.html
https://en.wikipedia.org/wiki/Neville’s algorithm
http://mathworld.wolfram.com/NevillesAlgorithm.html
https://reference.wolfram.com/language/ref/Interpolation.html
http://algolist.ru/maths/approx.php
Dmytro Mitin fb.com/dmitry.mitin Interpolation