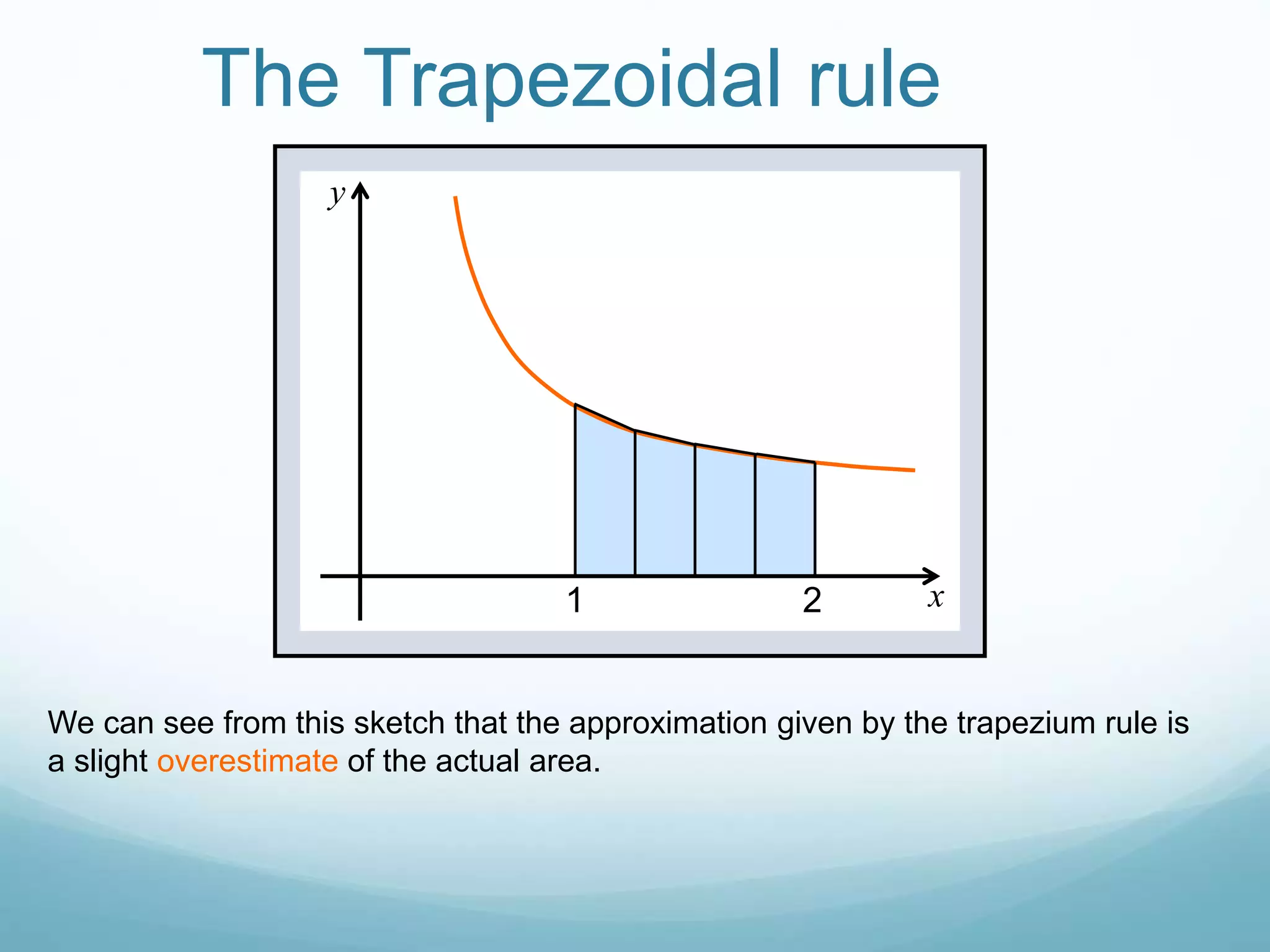
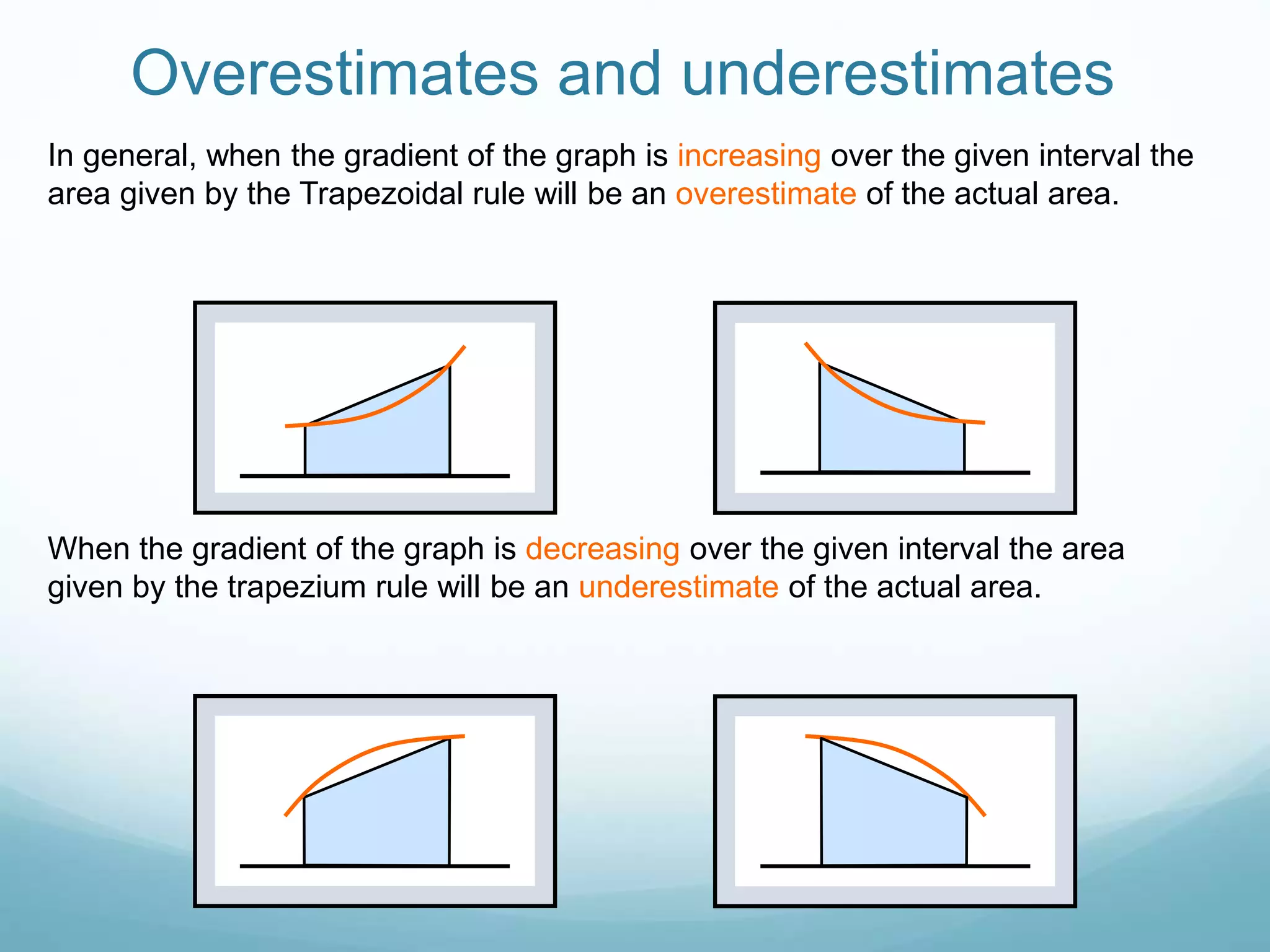
The Trapezoidal rule approximates the area under a curve by dividing it into trapezoids and calculating their individual areas. It works by taking the ordinates at evenly spaced intervals along the x-axis and using the formula: Area = (1/2) * (first ordinate + last ordinate + 2 * sum of middle ordinates) * width. This provides an estimate of the definite integral. The more trapezoids used, the more accurate the estimate. The estimate will be an overestimate if the gradient is increasing and an underestimate if decreasing over the interval.

1. Contents
The Trapezoidal Rule
to estimate areas underneath a
curve
x
y
a b

2. Approximating the area under a
curveSometimes the area under a curve cannot be found by integration.
This may be because we cannot find the integral of the equation of the curve or
because we need to find the area under a curve produced from experimental data.
In these cases we can use a method to approximate the area under the curve.
One such method is called the Trapezoidal rule.
It works by dividing the area under a curve into trapeziums and calculating their
areas. Remember:
The area of a trapezium = 1
2 ( )a b h
a
b
h a
b
h
or

3. The Trapezoidal rule
To demonstrate the method consider the area under the curve y = x2 + 1.

4. x
y
a b
The Trapezoidal rule
The more trapeziums the area is divided into the more accurate the estimate.
Suppose we wish to find the area under a curve y = f(x) between x = a and x = b.
y0 y1 y2 y3 y4
We can divide the area into
four trapeziums of equal width
h.
The parallel sides of the four
trapeziums are given by the
five ordinates y0, y1, y2, y3 and
y4.hhhh
In general, if there are n trapeziums there will be n + 1 ordinates.

5. The Trapezoidal rule
The approximate area using the Trapezoidal rule is:
1 1 1 1
0 1 1 2 2 3 3 42 2 2 2( ) ( + )+ ( + )+ ( + )+ ( + )
b
a
f x dx h y y h y y h y y h y y
1
0 1 1 2 2 3 3 42= ( + + + + + + + )h y y y y y y y y
1
0 1 2 3 42= ( +2 +2 +2 + )h y y y y y
The ordinates have to be spaced out evenly so that the width of each trapezium is
the same.
 for n trapeziums of equal width h:
=
b a
h
n

In general, the trapezium rule with n trapeziums is:
1
0 1 2 12( ) ( + 2 + 2 +...+ 2 + )
b
n na
f x dx h y y y y y

6. The Trapezoidal rule
Use the trapezoidal rule with four trapeziums to estimate the value of
State whether this is an overestimate or an underestimate of the actual area.
2
1
1
dx
x
We can use a table to record the value of each ordinate.
The width h of each trapezium =
2 1
= 0.25
4

0.50.5710.6670.81
21.751.51.251x
1
=y
x
y4y3y2y1y0

7. The Trapezoidal rule
We can now work out the area using
1
0 1 2 12( ) ( + 2 + 2 +...+ 2 + )
b
n na
f x dx h y y y y y
with h = 0.25 and the ordinates given by the table, so:
2
1
1
dx
x
  
1
×0.25× 1+ 2(0.8)+ 2(0.667)+ 2(0.571)+0.5
2
= 0.70 (to 2 d.p.)
We can show whether this is an underestimate or an overestimate by sketching the
area given by the trapezium rule on the graph of
1
=y
x

8. The Trapezoidal rule
x
y
We can see from this sketch that the approximation given by the trapezium rule is
a slight overestimate of the actual area.
21

9. Overestimates and underestimates
In general, when the gradient of the graph is increasing over the given interval the
area given by the Trapezoidal rule will be an overestimate of the actual area.
When the gradient of the graph is decreasing over the given interval the area
given by the trapezium rule will be an underestimate of the actual area.

10. Examination-style question
a) Use the Trapezoidal rule with 4 ordinates to estimate to 2
decimal places the value of
b) State whether the estimate given in part a) is an
overestimate or underestimate of the area under the curve
y = tan x between x = 0 and x = .3

3
0
tan xdx


Using a table to record the value of each ordinate:
The width h of each trapezium = 3
=
3 9


1.7320.8390.3640y = tan x
0x
9
 2
9

3


11. Examination-style question
We can now work out the area using
1
0 1 2 12( ) ( + 2 + 2 +...+ 2 + )
b
n na
f x dx h y y y y y
 × 0 + 2(0.364)+ 2(0.839)+1.732
18

= 0.72 (to 2 d.p.)
b) Sketching the curve y = tan x
shows that the value given
in a) is a slight overestimate
of the actual area.
with h = and the ordinates given by the table, so:
9

3
0
tan xdx


0 x
y
3
