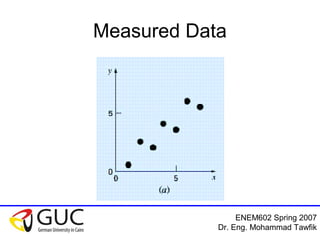
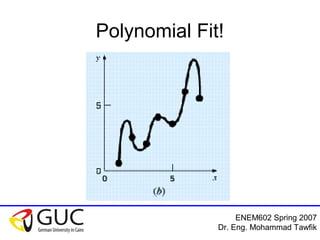
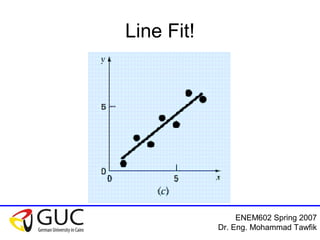
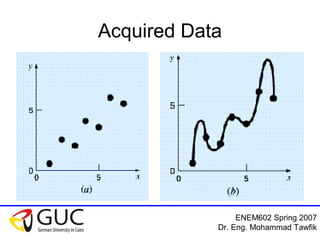
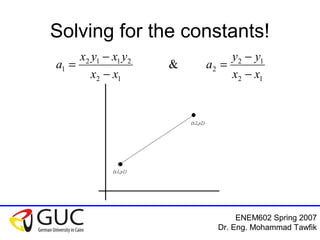
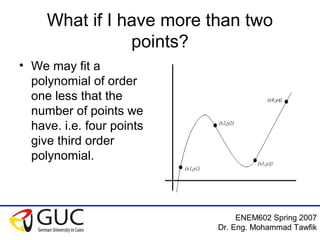
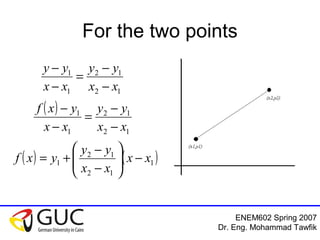
This document outlines a course on interpolation and curve fitting taught by Dr. Eng. Mohammad Tawfik. It discusses the objectives of understanding the differences between regression and interpolation and how to fit polynomials to data. It provides examples of using linear, polynomial, and Newton's interpolation methods to find equations that fit sets of measured data points, including solving systems of equations and using tables. The document emphasizes that Newton's method has the advantage of not requiring matrix inversion.

1. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Interpolation/Curve Fitting

2. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Objectives
• Understanding the difference between
regression and interpolation
• Knowing how to “best fit” a polynomial into
a set of data
• Knowing how to use a polynomial to
interpolate data

3. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Measured Data

4. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Polynomial Fit!

5. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Line Fit!

6. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Which is better?

7. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Curve Fitting
• If the data measured is of high accuracy
and it is required to estimate the values of
the function between the given points,
then, polynomial interpolation is the
best choice.
• If the measurements are expected to be of
low accuracy, or the number of
measured points is too large, regression
would be the best choice.

8. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Interpolation

9. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Why Interpolation?
• When the accuracy of your measurements
are ensured
• When you have discrete values for a
function (numerical solutions, digital
systems, etc …)

10. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Acquired Data

11. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
But, how to get the equation of a
function that passes by all the
data you have!

12. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Equation of a Line: Revision
xaay 21 +=
If you have two points
1211 xaay +=
2212 xaay += 





=












2
1
2
1
2
1
1
1
y
y
a
a
x
x

13. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solving for the constants!
12
12
2
12
2112
1 &
xx
yy
a
xx
yxyx
a
−
−
=
−
−
=

14. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
What if I have more than two
points?
• We may fit a
polynomial of order
one less that the
number of points we
have. i.e. four points
give third order
polynomial.

15. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Third-Order Polynomial
3
4
2
321 xaxaxaay +++=
For the four points
3
14
2
131211 xaxaxaay +++=
3
24
2
232212 xaxaxaay +++=
3
34
2
333213 xaxaxaay +++=
3
44
2
434214 xaxaxaay +++=

16. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
In Matrix Form














=




























4
3
2
1
4
3
2
1
3
4
2
24
3
3
2
23
3
2
2
22
3
1
2
11
1
1
1
1
y
y
y
y
a
a
a
a
xxx
xxx
xxx
xxx
Solve the above equation for the constants of the polynomial.

17. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton's Interpolation
Polynomial

18. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method
• In the previous procedure, we needed to solve a
system of linear equations for the unknown
constants.
• This method suggests that we may just proceed
with the values of x & y we have to get the
constants without setting a set of equations
• The method is similar to Taylor’s expansion
without differentiation!

19. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Equation of a Line: Revision
xaay 21 +=
If you have two points
1211 xaay +=
2212 xaay += 





=












2
1
2
1
2
1
1
1
y
y
a
a
x
x

20. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
For the two points
12
12
1
1
xx
yy
xx
yy
−
−
=
−
−
( )
12
12
1
1
xx
yy
xx
yxf
−
−
=
−
−
( ) ( )1
12
12
1 xx
xx
yy
yxf −





−
−
+=

21. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
For the three points
( ) ( )
( )( )213
121
xxxxa
xxaaxf
−−+
−+=
11 ya =
12
12
2
xx
yy
a
−
−
=
13
12
12
23
23
3
xx
xx
yy
xx
yy
a
−
−
−
−
−
−
=

22. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Using a table
xi yi
x1 y1
x2 y2
x3 y3
13
12
12
23
23
xx
xx
yy
xx
yy
−
−
−
−
−
−
12
12
xx
yy
−
−
23
23
xx
yy
−
−

23. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
In General
• Newton’s Interpolation is performed for an
nth
order polynomial as follows
( ) ( ) ( )( )
( ) ( )nn xxxxa
xxxxaxxaaxf
−−++
−−+−+=
+ ...... 11
213121

24. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example
• Find a 3rd
order
polynomial to
interpolate the
function described by
the given points
x Y
-1 1
0 2
1 5
2 16

25. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution: System of equations
• A third order polynomial is given by:
( ) 3
4
2
321 xaxaxaaxf +++=
( ) 11 4321 =−+−=− aaaaf
( ) 20 1 == af
( ) 51 4321 =+++= aaaaf
( ) 168422 4321 =+++= aaaaf

26. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
In matrix form














=

























 −−
16
5
2
1
8421
1111
0001
1111
4
3
2
1
a
a
a
a














=














1
1
1
2
4
3
2
1
a
a
a
a
( ) 32
2 xxxxf +++=

27. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method
• Newton’s methods defines the polynomial in the
form:
( ) ( ) ( )( )
( )( )( )3214
213121
xxxxxxa
xxxxaxxaaxf
−−−+
−−+−+=
( ) ( ) ( )( )
( )( )( )11
11
4
321
−++
++++=
xxxa
xxaxaaxf

28. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method
x Y
-1 1 1 1 1
0 2 3 4
1 5 11
2 16

29. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Newton’s Method
• Finally:
( ) ( ) ( )( )
( )( )( )11
111
−++
++++=
xxx
xxxxf
( ) ( ) ( ) ( )xxxxxxf −+++++= 32
11
( ) 32
2 xxxxf +++=

30. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Advantage of Newton’s Method
• The main advantage of Newton’s method
is that you do not need to invert a matrix!

31. ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Homework #6
• Chapter 18, pp. 505-506, numbers:
18.1, 18.2, 18.3, 18.5.