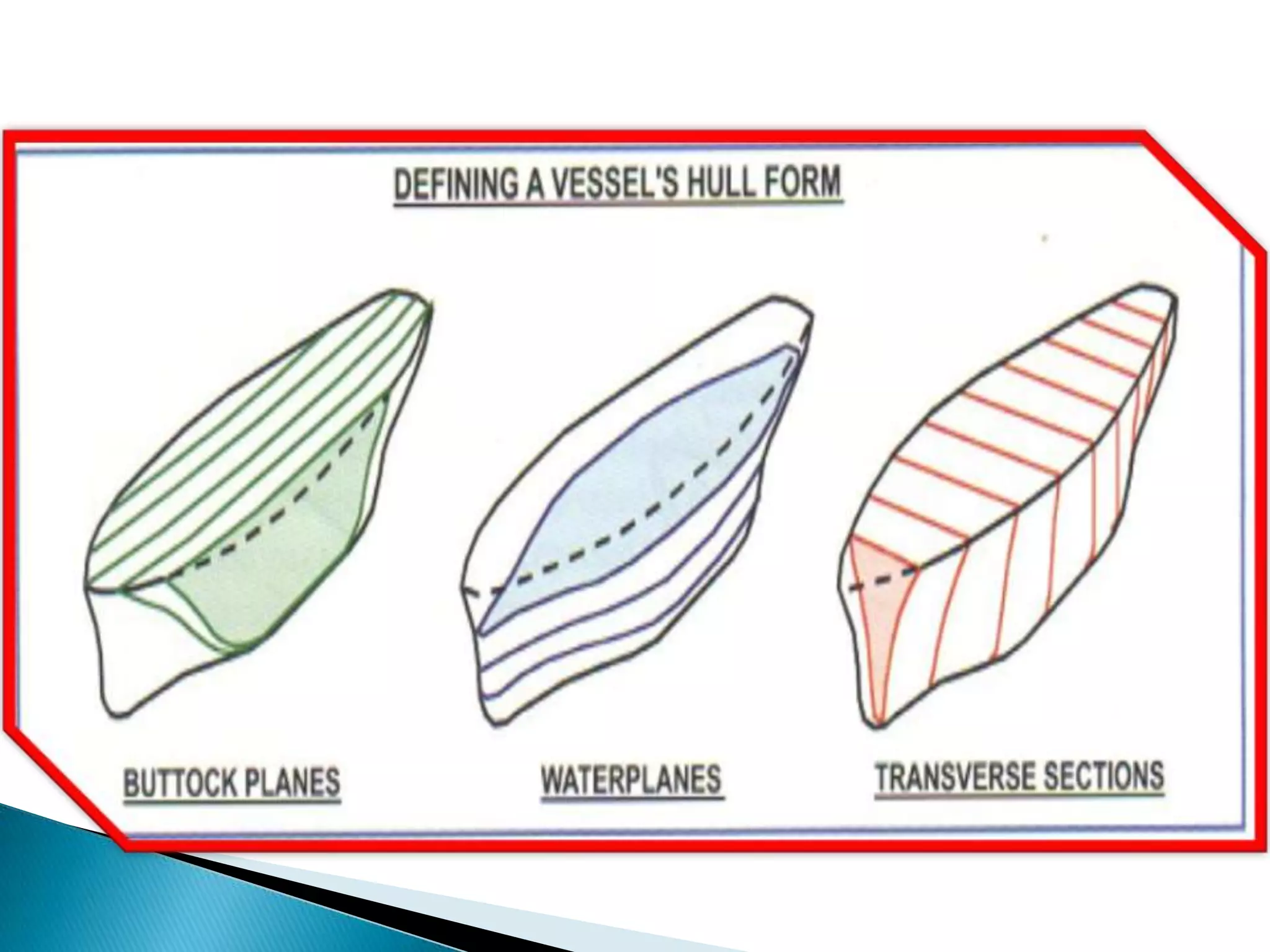
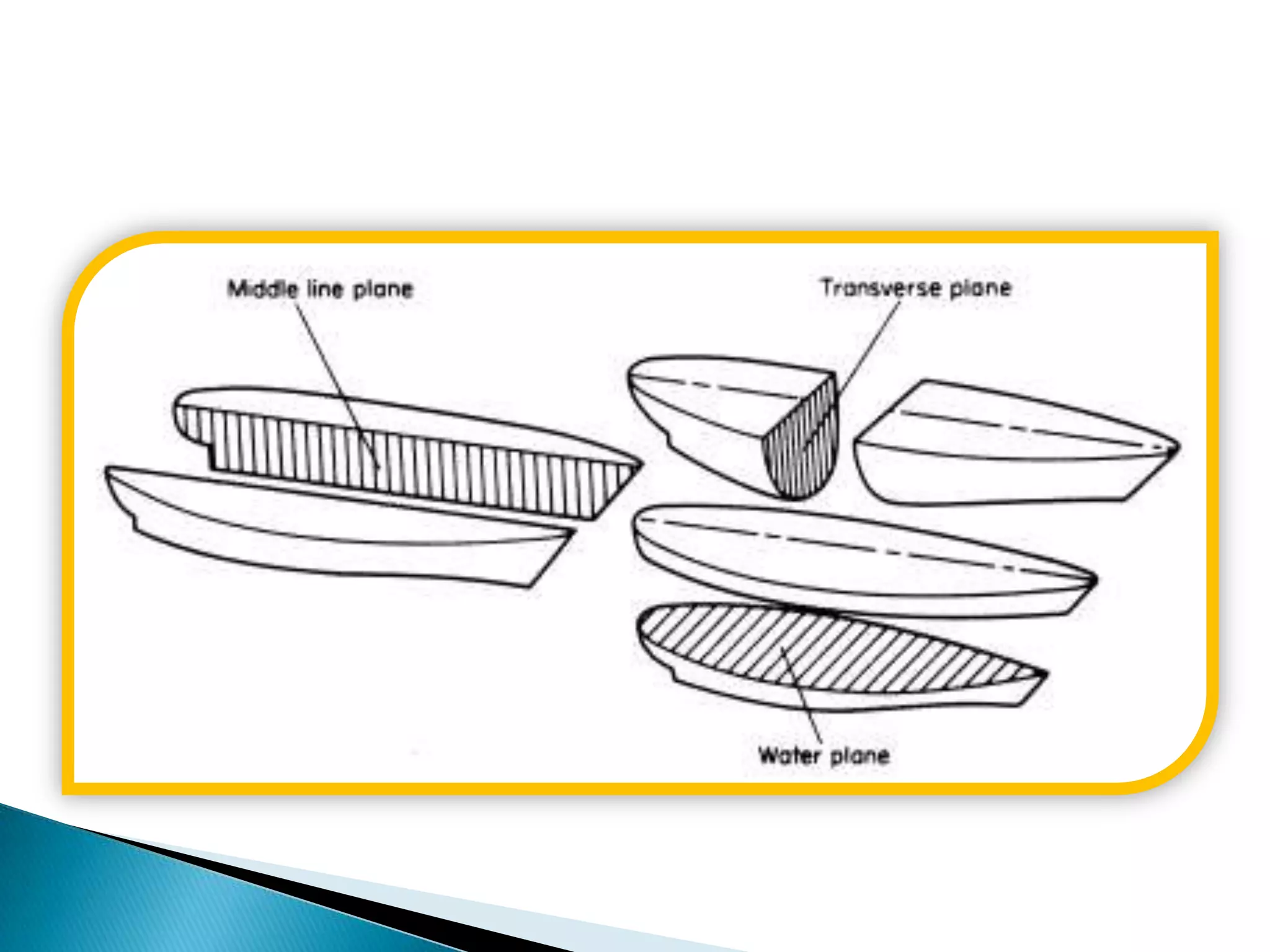
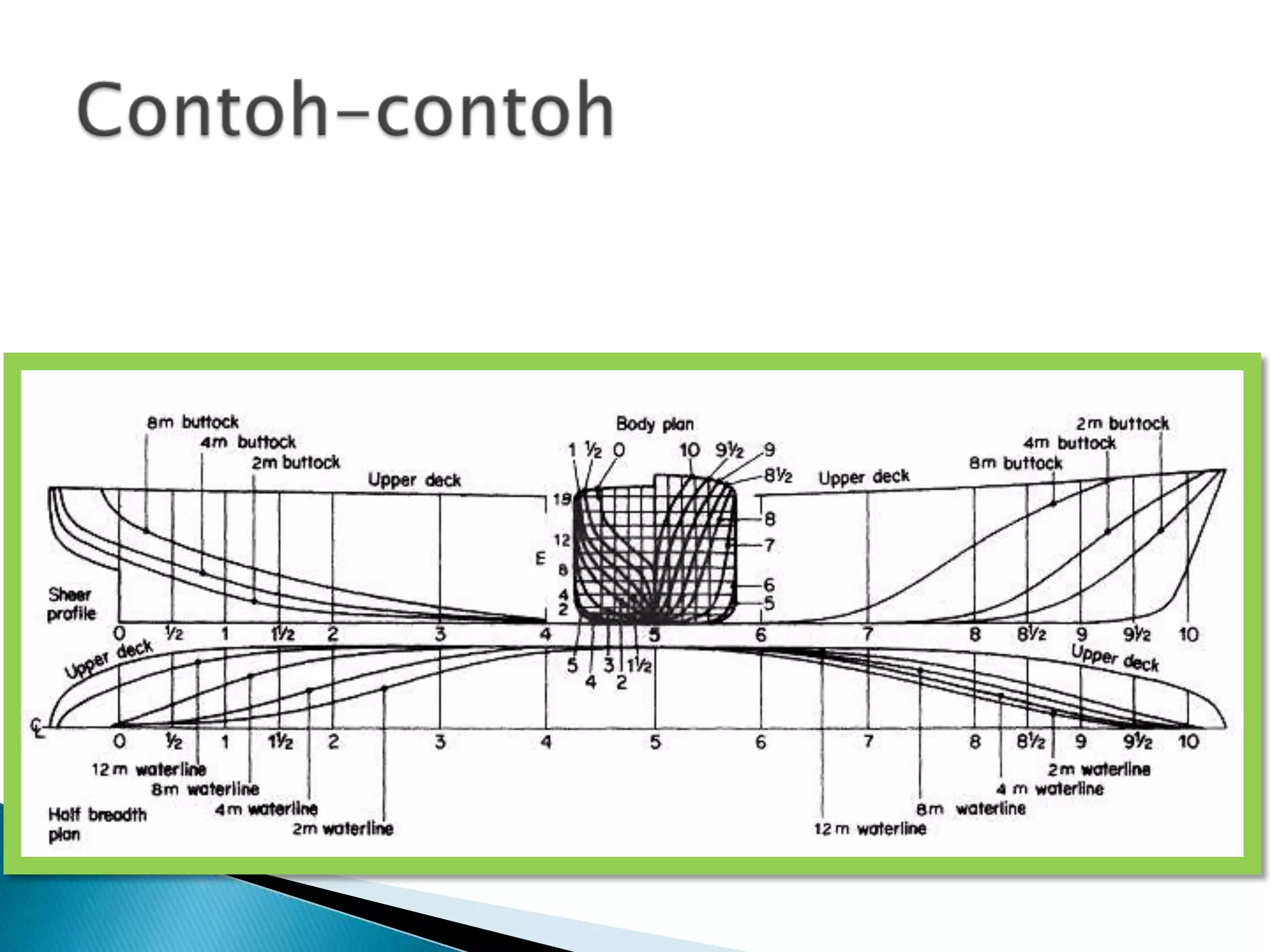
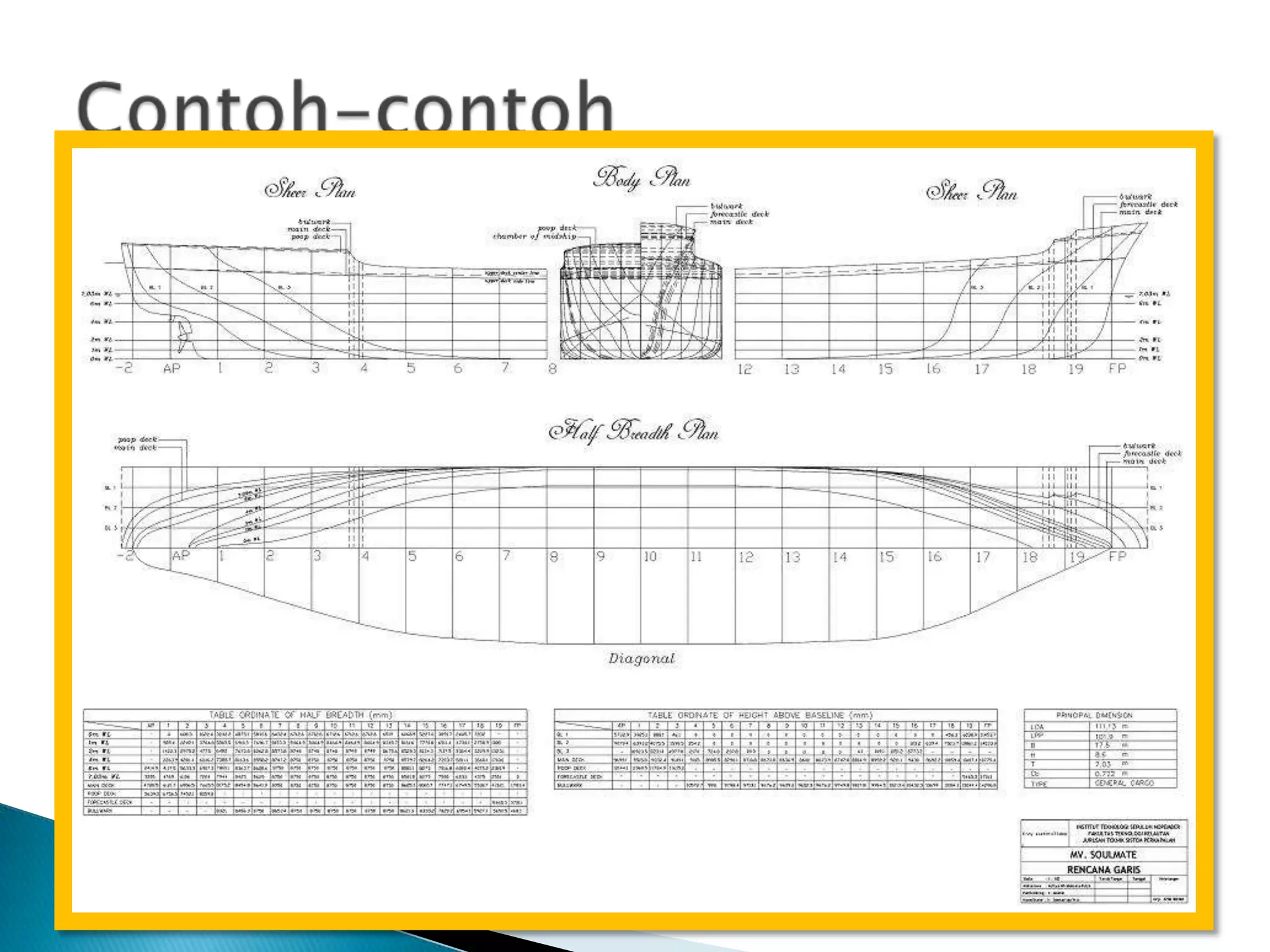
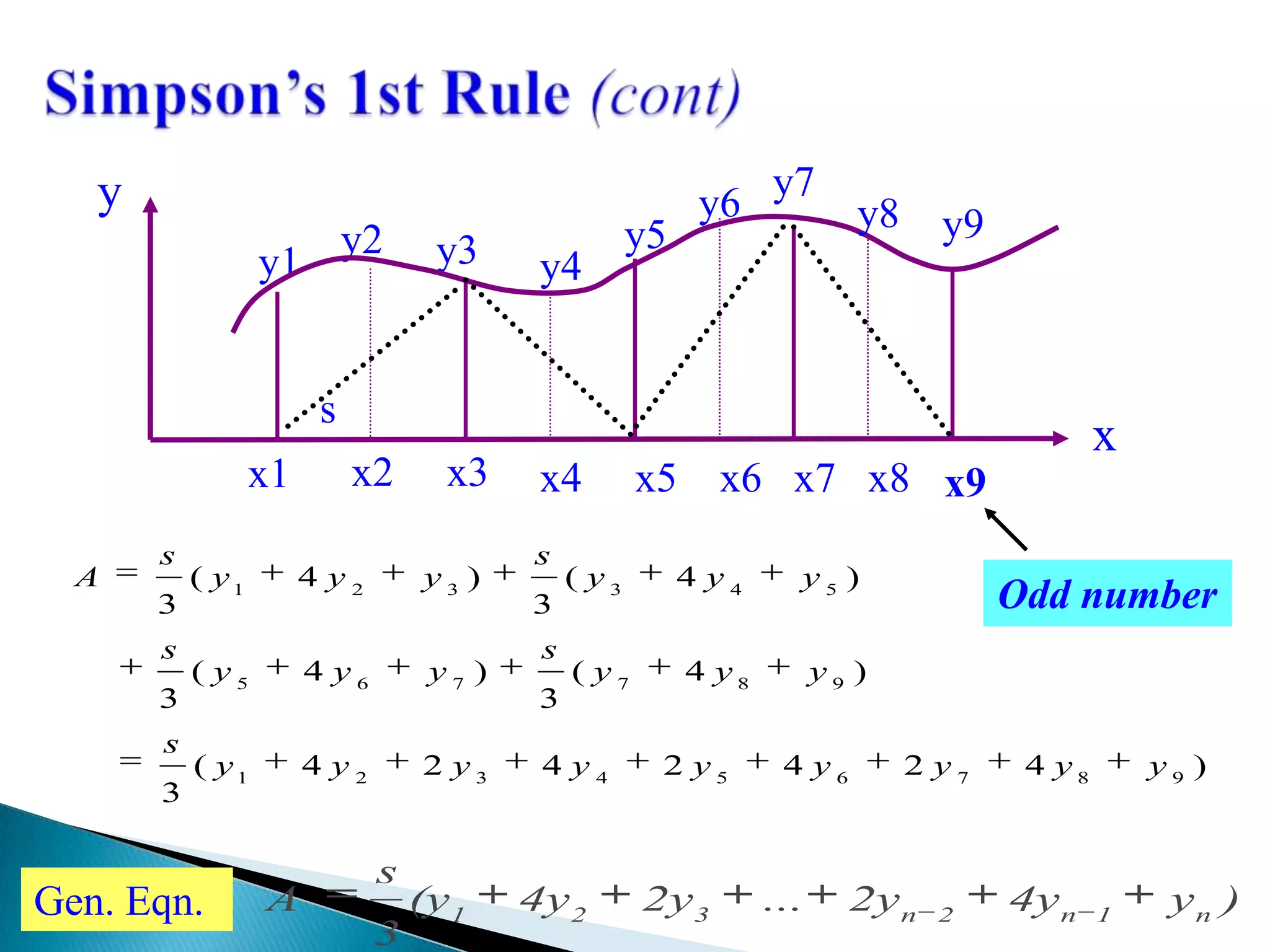
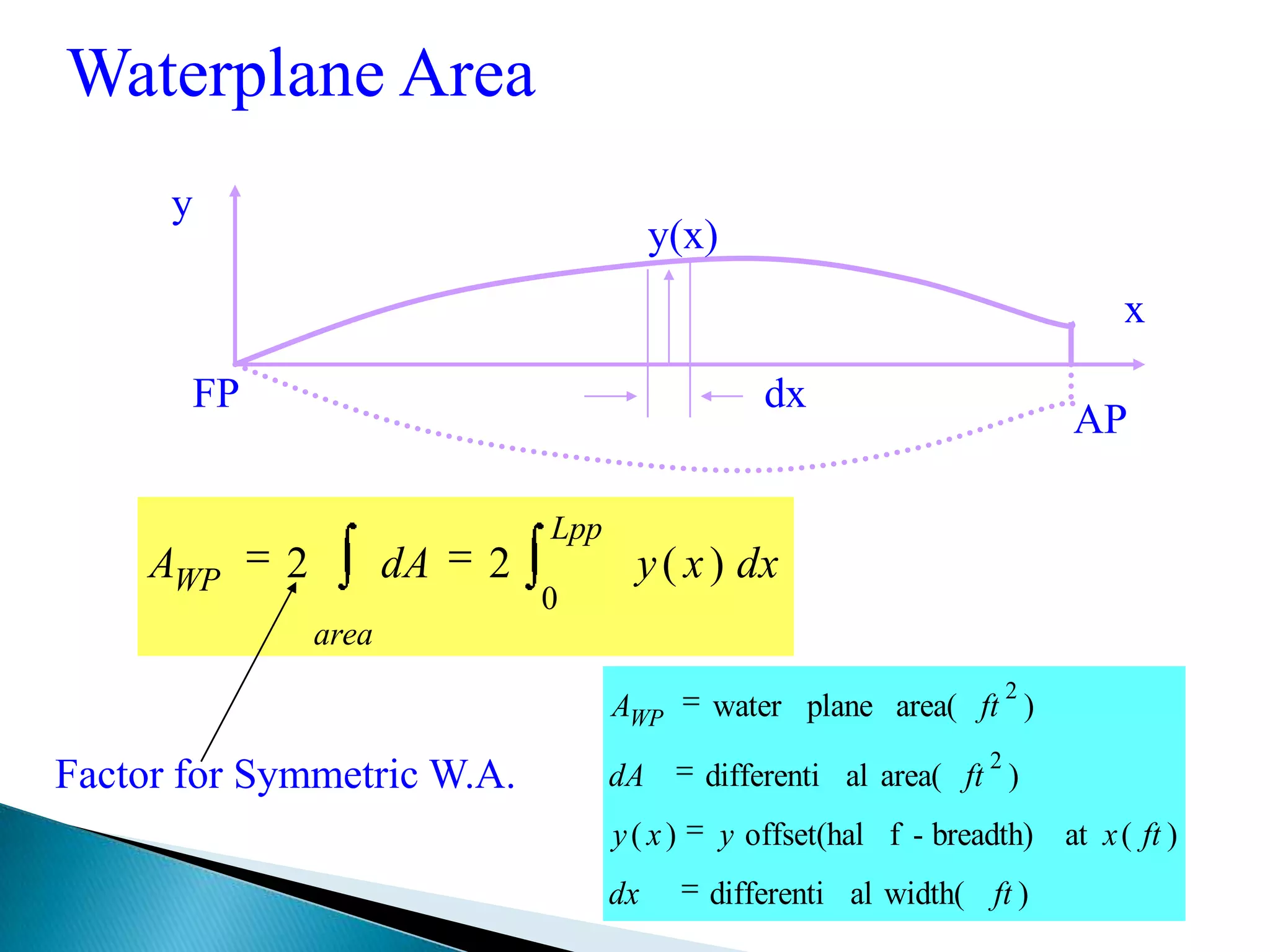
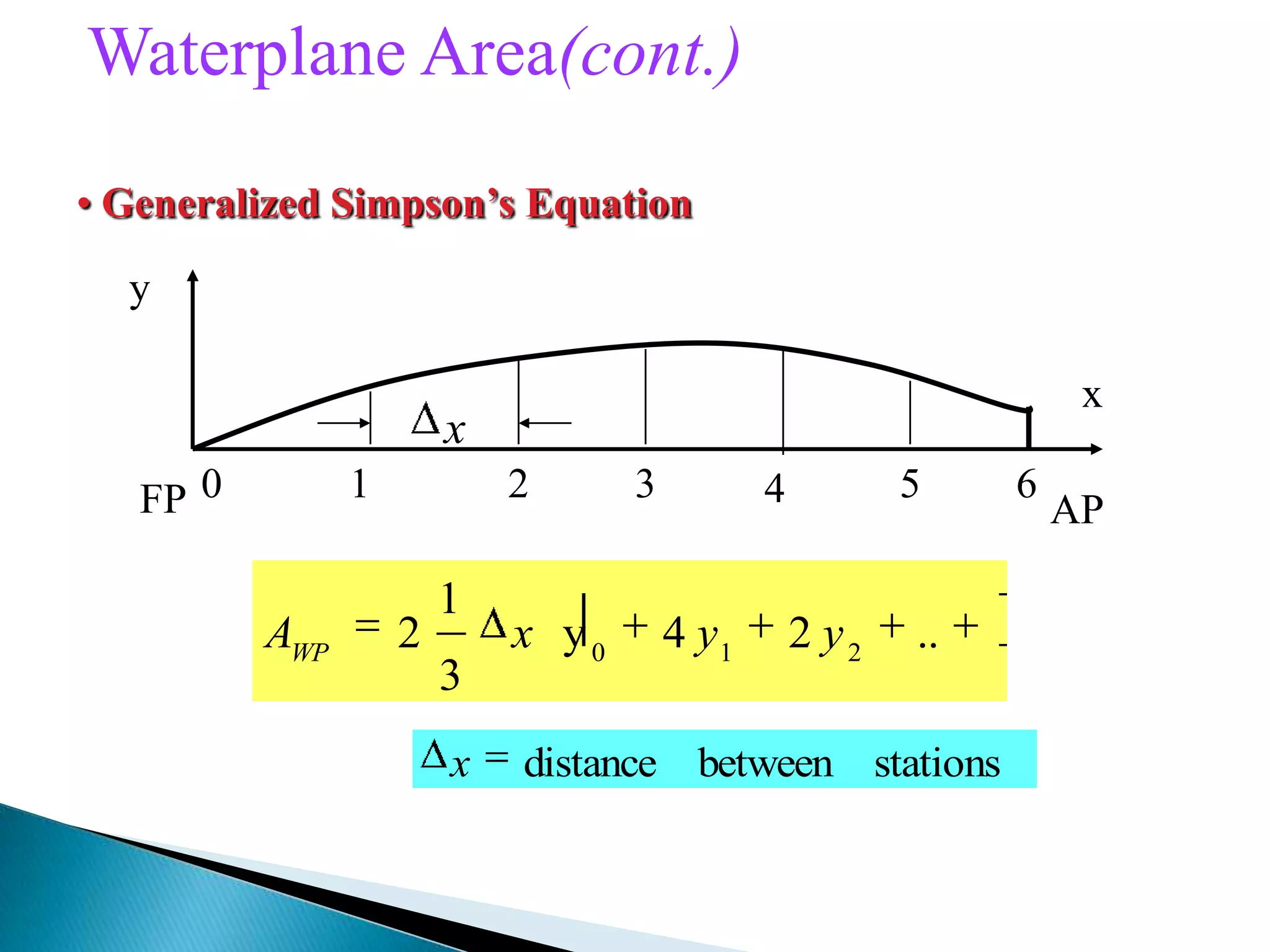
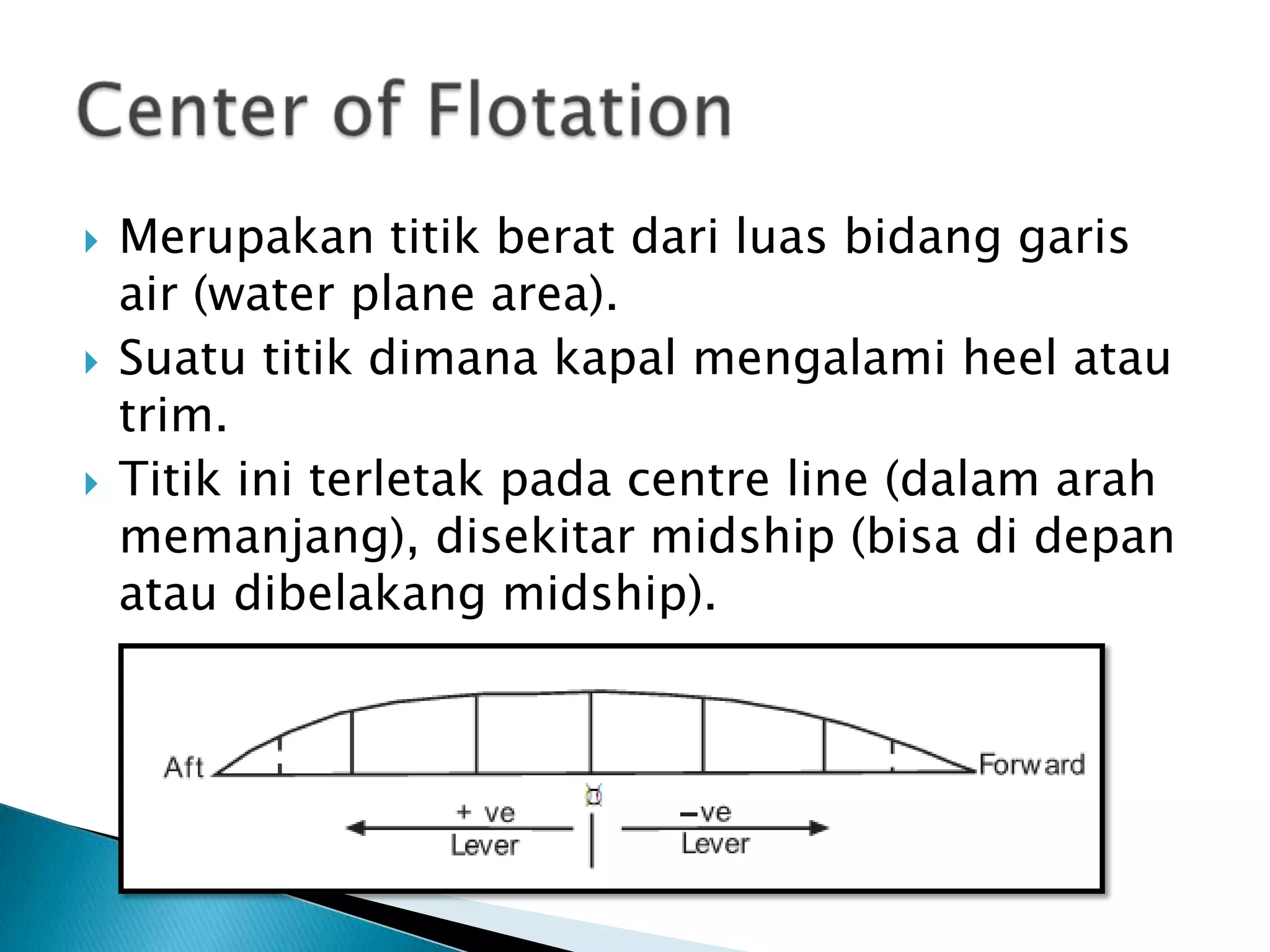
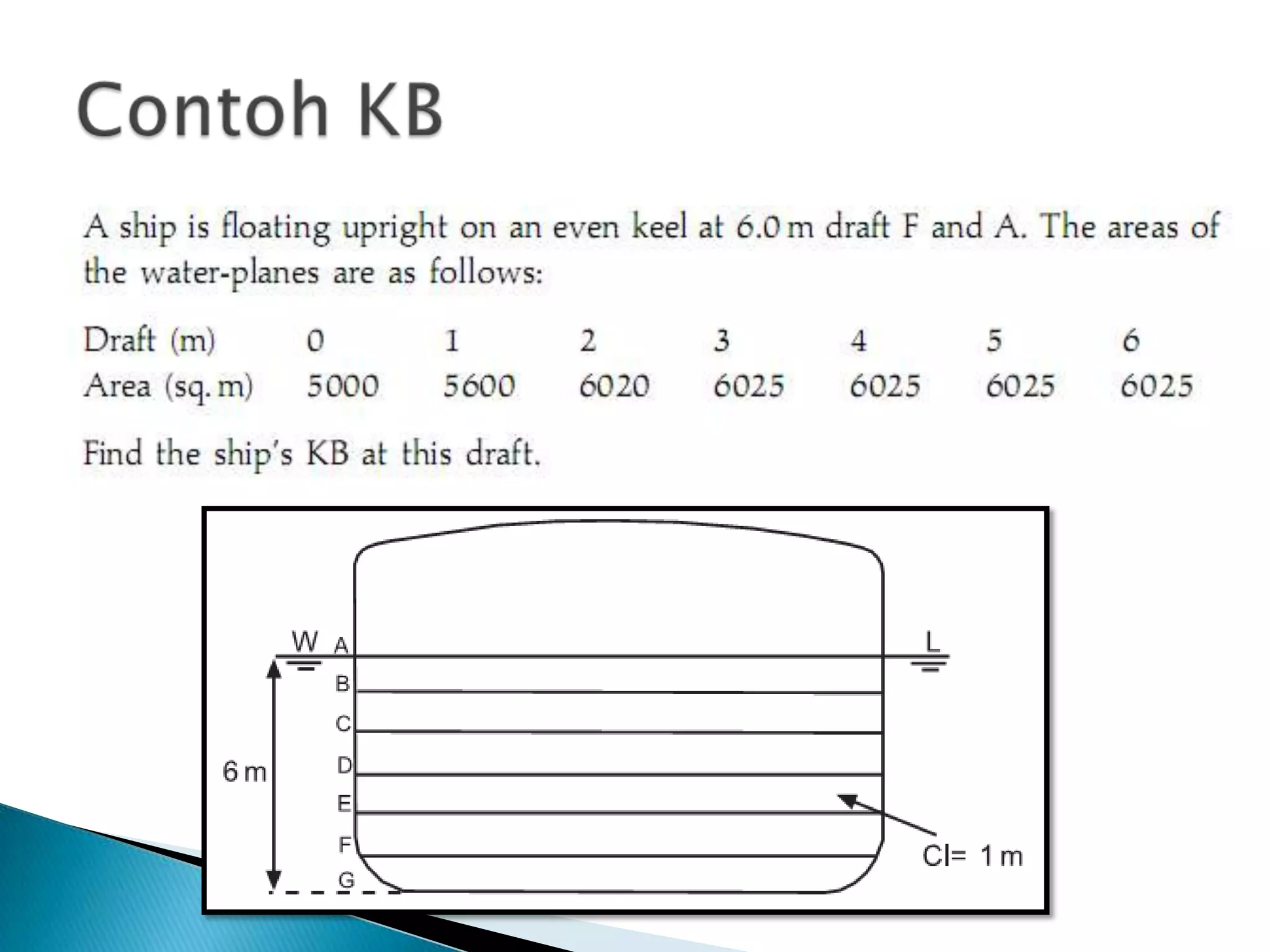
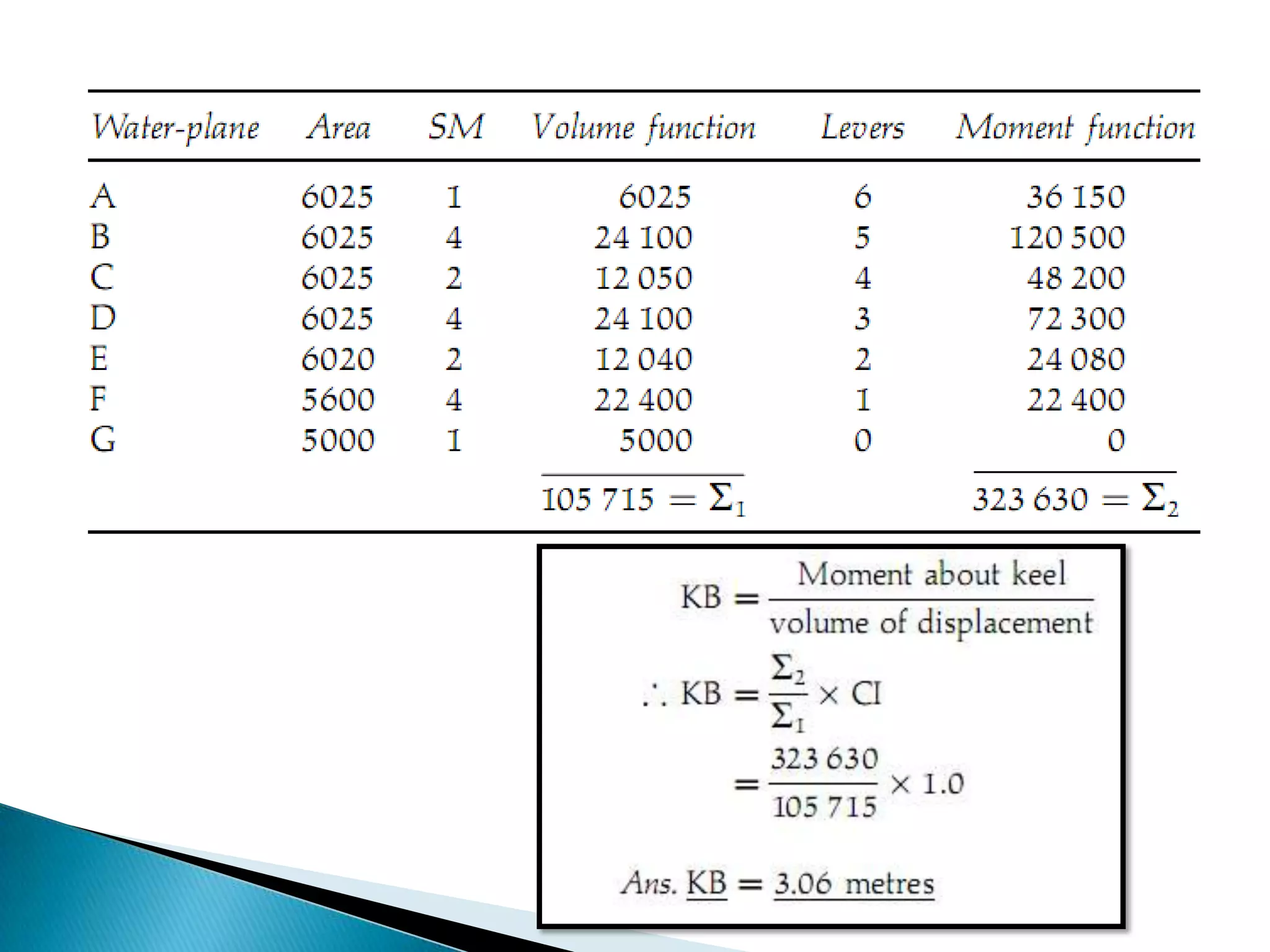
This document discusses numerical integration methods for calculating ship geometrical properties. It introduces the Trapezoidal rule, Simpson's 1st rule, and Simpson's 2nd rule for numerical integration when the ship's shape cannot be represented by a mathematical equation. It then provides examples of applying Simpson's 1st rule to calculate properties like waterplane area, sectional area, submerged volume, and the longitudinal center of floatation (LCF). The document explains the calculation steps and provides generalized Simpson's equations for these examples.

1. Adi Wirawan Husodo

2.  Why numerical integration?
◦ Ship is complex and its shape cannot usually be
presented by mathematical equation.
◦ Numerical scheme, therefore, should be used to
calculate the ship’s geometrical properties.
 Which numerical method ?
◦ Trapezoidal rule
◦ Simpson’s 1st rule
◦ Simpson’s 2nd rule

8. - uses 2 data points
- assume linear curve
x1 x2 x3 x4
s s s
y1
y2 y3
y4
A1 A2 A3
: y=ax+b
Total Area = A1+A2+A3
= s/2 (y1+2y2+2y3+y4)
A1=s/2 (y1+y2)
A2=s/2 (y2+y3)
A3=s/2 (y3+y4)

9. - uses 3 data points
- assume 2nd order polynomial curve
Area : )4(
3
321
3
1
yyy
s
dxydAA
x
x
x1 x3
y(x)=ax²+bx+c
x
y
A
dx
x1 x2 x3s
y1 y2 y3
x
y
AdA
Mathematical Integration Numerical Integration
x2
s
y(x)=ax²+bx+c

10. x1 x2 x3
s
y1
y2 y3
x
y
x4 x5 x6 x7 x8 x9
y4
y5
y6
y7
y8 y9
Gen. Eqn.
Odd number
)y4y2y...2y4y(y
3
s
A n1n2n321
)4242424(
3
)4(
3
)4(
3
)4(
3
)4(
3
987654321
987765
543321
yyyyyyyyy
s
yyy
s
yyy
s
yyy
s
yyy
s
A

11. - uses 4 data points
- assume 3rd order polynomial curve
x1 x2 x3
s s
y1
y2 y3
y(x)=ax³+bx²+cx+d
x
y
Area : )33(
8
3
4321 yyyy
s
A
A
x4
y4
Simpson’s 2nd Rule (skip)

12. Application of Numerical Integration
• Application
- Waterplane Area
- Sectional Area
- Submerged Volume
- LCF
- VCB
- LCB
• Scheme
- Simpson’s 1st Rule

13. Numerical Calculation
• Calculation Steps
1. Start with a picture of what you are about to integrate.
2. Show the differential element you are using.
3. Properly label your axis and drawing.
4. Write out the generalized calculus equation written in
the same symbols you used to label your picture .
5. Write out Simpson’s equation in generalized form.
6. Substitute each number into the generalized Simpson’s
equation.
7. Calculate final answer.
Not optional ! Always follow the above steps!

14. Waterplane Area
y
x
dxFP
AP
y(x)
area
Lpp
WP dxxydAA
0
)(22
)width(aldifferenti
)(atbreadth)-foffset(hal)(
)area(aldifferenti
)area(planewater
2
2
ftdx
ftxyxy
ftdA
ftAWP
Factor for Symmetric W.A.

15. Waterplane Area(cont.)
• Generalized Simpson’s Equation
..24y
3
1
2 210
yyxAWP
stationsbetweendistancex
y
x
FP AP
0 1 2 3 4 5 6
x

16. Sectional Area
• Sectional Area : Numerical integration of half-breadth
as a function of draft
WL
z
y
dz
y(z)
T
area
T
t dzzydAA
0
sec )(22
)width(aldifferenti
)z(atbreadth)-foffset(hal)(
)area(aldifferenti
)(toupareasectional
2
2
sec
ftdz
ftyzy
ftdA
ftzA t

17. Sectional Area(cont.)
• Generalized Simpson’s equation
swaterlinebetweendistancez
nn
area
T
t
yyyyz
dzzydAA
1210
0
sec
4..24y
3
1
2
)(22
z
y
WL
T
0
2
4
6
8
z

18. Submerged Volume : Longitudinal Integration
• Submerged Volume : Integration of sectional area over
the length of ship
• Scheme z
x
y
)( xAs

19. Submerged Volume
• Sectional Area Curve
• Calculus equation
volume
L
tssubmerged
pp
dxxAdVV
0
sec )(
x
As
FP AP
dx
)(sec xA t
• Generalized equation
nns
yyyyx 1210
4..24y
3
1
stationsbetweendistancex

20. Longitudinal Center of Floatation (LCF)
• LCF
- Centroid of waterplane area
- Distance from reference point to center of floatation
- Referenced to amidships or FP
- Sign convention of LCF
+
+
-
FP
WL

21.  Merupakan titik berat dari luas bidang garis
air (water plane area).
 Suatu titik dimana kapal mengalami heel atau
trim.
 Titik ini terletak pada centre line (dalam arah
memanjang), disekitar midship (bisa di depan
atau dibelakang midship).

25.  Disebut juga dengan KB (Keel to Buoyancy)
 Merupakan titik berat dari volume
displacement kapal
 KB atau VCB =
ntdisplacemevol.
keelabout themomenttotal