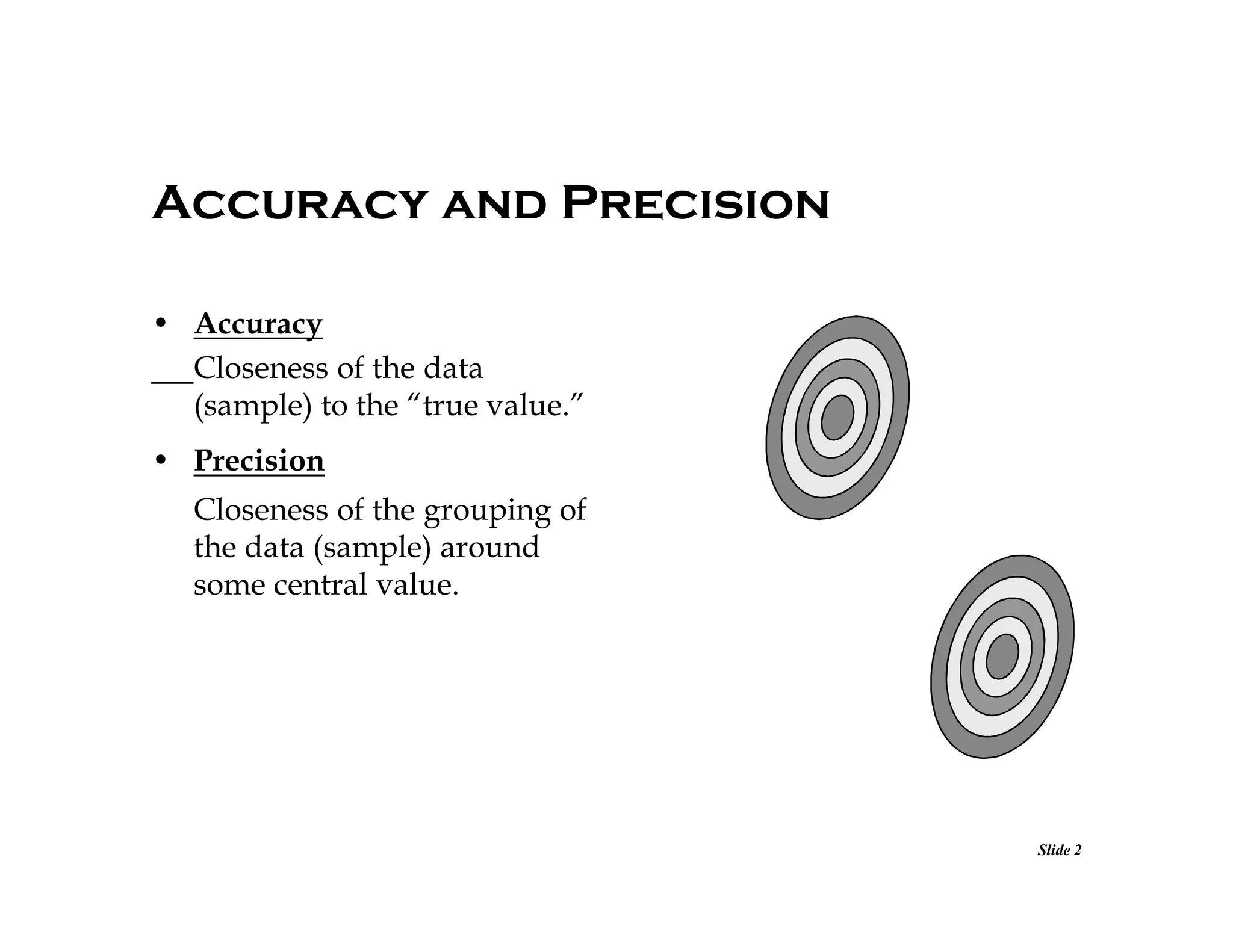
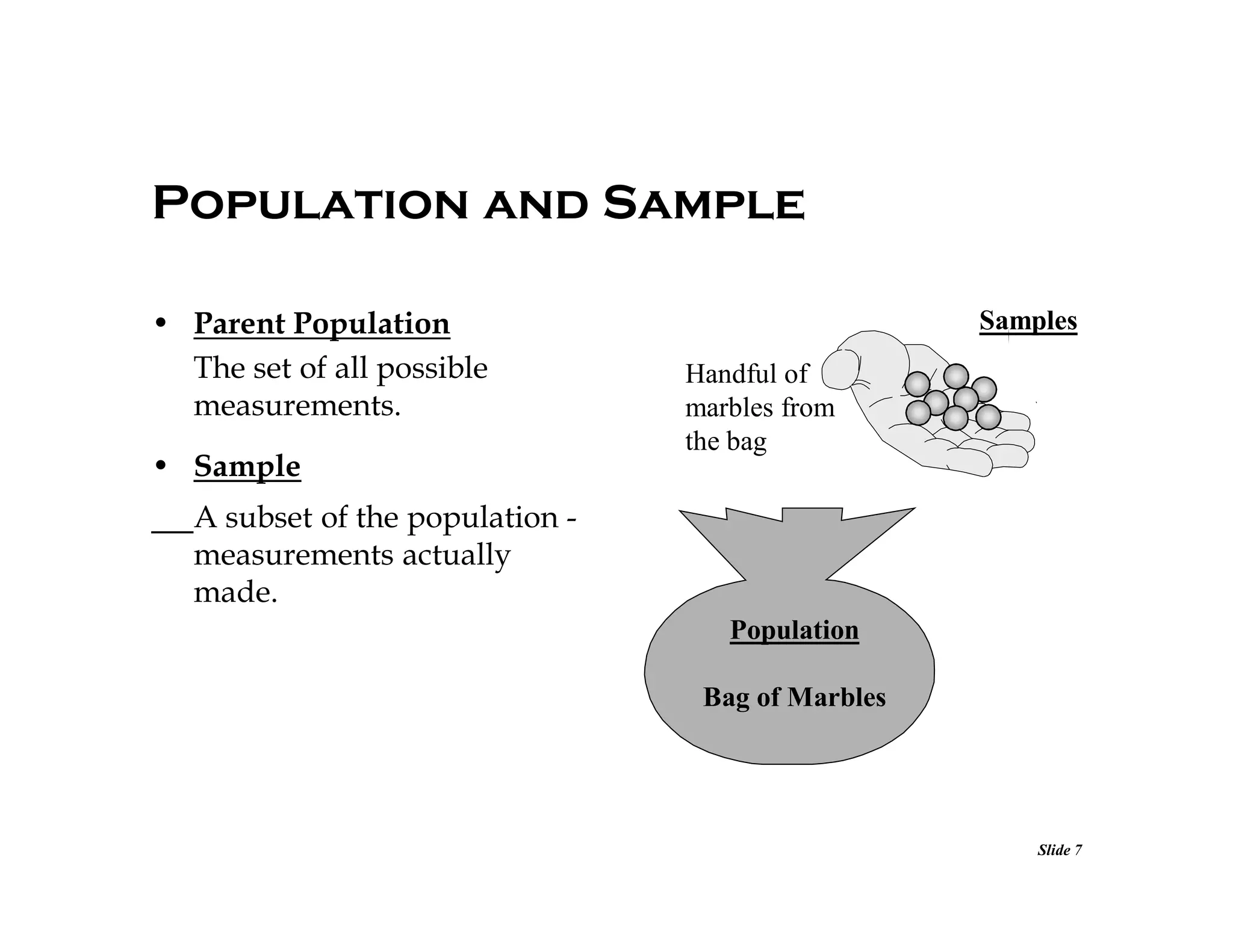
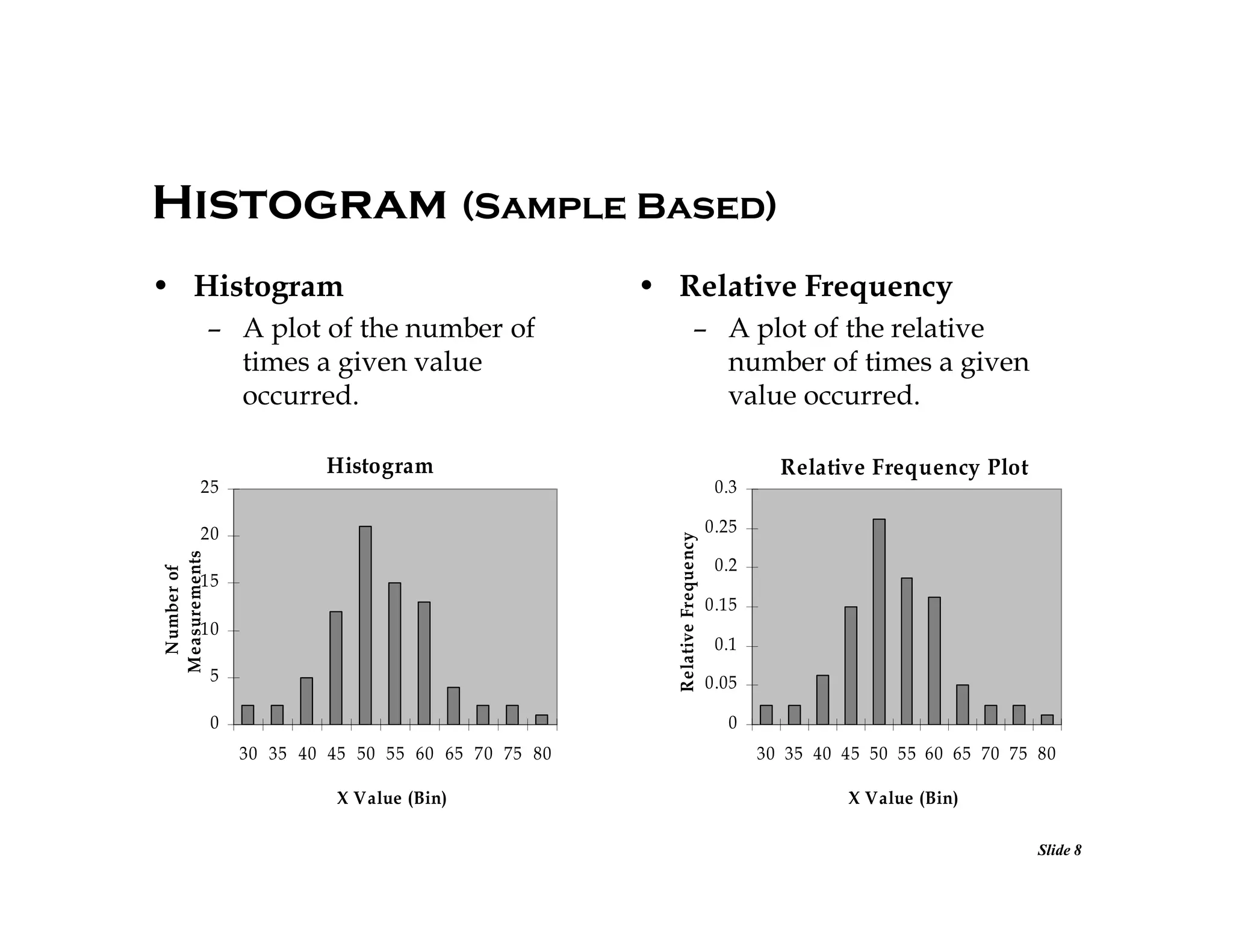
This document discusses concepts related to error analysis and statistics. It covers accuracy and precision, individual measurement uncertainty including means, variance, standard deviation and confidence intervals. It also discusses uncertainty when calculating quantities from multiple measurements using error propagation. Additionally, it discusses least squares fitting of data. Key points include how to quantify accuracy and precision, characterize the distribution of data, calculate uncertainty intervals, and propagate errors through calculations involving multiple measured variables.

1. Error Analysis - Statistics
• Accuracy and Precision
• Individual Measurement Uncertainty
– Distribution of Data
– Means, Variance and Standard Deviation
– Confidence Interval
• Uncertainty of Quantity calculated from several
Measurements
– Error Propagation
• Least Squares Fitting of Data
Slide 1

2. Accuracy and Precision
• Accuracy
Closeness of the data
(sample) to the “true value.”
• Precision
Closeness of the grouping of
the data (sample) around
some central value.
Slide 2

3. Accuracy and Precision
• Precise but Inaccurate
Relative Frequency
Relative Frequency
• Inaccurate & Imprecise
True Value
X Value
True Value
X Value
Slide 3

4. Accuracy and Precision
• Precise and Accurate
Relative Frequency
Relative Frequency
• Accurate but Imprecise
True Value
X Value
True Value
X Value
Slide 4

5. Accuracy and Precision
Q: How do we quantify the concept of accuracy and
precision? -- How do we characterize the error that
occurred in our measurement?
Slide 5

6. Individual Measurement
Statistics
• Take N measurements: X1, . . . , XN
• Calculate mean and standard deviation:
1
x
N
Sx
2
N
X
i
i 1
1 N
2

 X i   x  
N  i 1


• What to use as the “best value” and uncertainty so
we can say we are Q% confident that the true value
lies in the interval xbest 
x.
• Need to know how data is distributed.
Slide 6

7. Population and Sample
• Parent Population
The set of all possible
measurements.
• Sample
Samples
Handful of
marbles from
the bag
A subset of the population measurements actually
made.
Population
Bag of Marbles
Slide 7

8. Histogram (Sample Based)
• Histogram
– A plot of the number of
times a given value
occurred.
• Relative Frequency
– A plot of the relative
number of times a given
value occurred.
Histogram
20
Relative Frequency Plot
0.25
Relative Frequency
0.3
Number of
Measurements
25
15
10
5
0
0.2
0.15
0.1
0.05
0
30 35 40 45 50 55 60 65 70 75 80
30 35 40 45 50 55 60 65 70 75 80
X Value (Bin)
X Value (Bin)
Slide 8

9. Probability Distribution (Population Based)
• Probability Density
Function (pdf) (p(x))
– Describes the probability
distribution of all possible
measures of x.
– Limiting case of the relative
frequency.
Probability Density Function
Probability per unit
change in x
0.3
• Probability Distribution
Function (P(x))
P x   P[ X  x]
X x
Probability that
– Probability Distribution
Function is the integral of
the pdf, i.e.
x
P  x    p  x  dx

0.25
Q: Plot the probability distribution function
vs x.
Q: What is the maximum value of P(x)?
0.2
0.15
0.1
0.05
0
30 35 40 45 50 55 60 65 70 75 80
x Value (Bin)
Slide 9

10. Probability Density Function
– The probability that a
measurement X takes value
between (-) is 1.


 p x  dx  1
– Every pdf satisfies the above
property.
Ex:
1 
p x  
e
A
x2
B
is a probability density function.
Find the relationship between A
and B.

 Hint:


0
2
e - a x dx 
1
2


a
Q: Given a pdf, how would one find the
probability that a measurement is
between A and B?
Slide 10

11. Common Statistical Distributions
• Gaussian (Normal) Distribution
p  x 
where: x
x
x
x2
1
 x 2

e
 x   x 2
p x
2  x2
= measured value
= true (mean) value
= standard deviation
= variance
Q: What are the two parameters that define a
Gaussian distribution?
x Value
Q: How would one calculate the probability
of a Gaussian distribution between x1
and x2? ( See Chapter 4, Appendix A )
Slide 11

12. Common Statistical Distributions
• Uniform Distribution
p x  
1
x2  x1
0
x1  x  x2
p x 
otherwise
where: x = measured value
x1 = lower limit
x2 = upper limit
x Value
Q: Why do x1 and x2 also define the magnitude of
the uniform distribution PDF?
Slide 12

13. Common Statistical Distributions
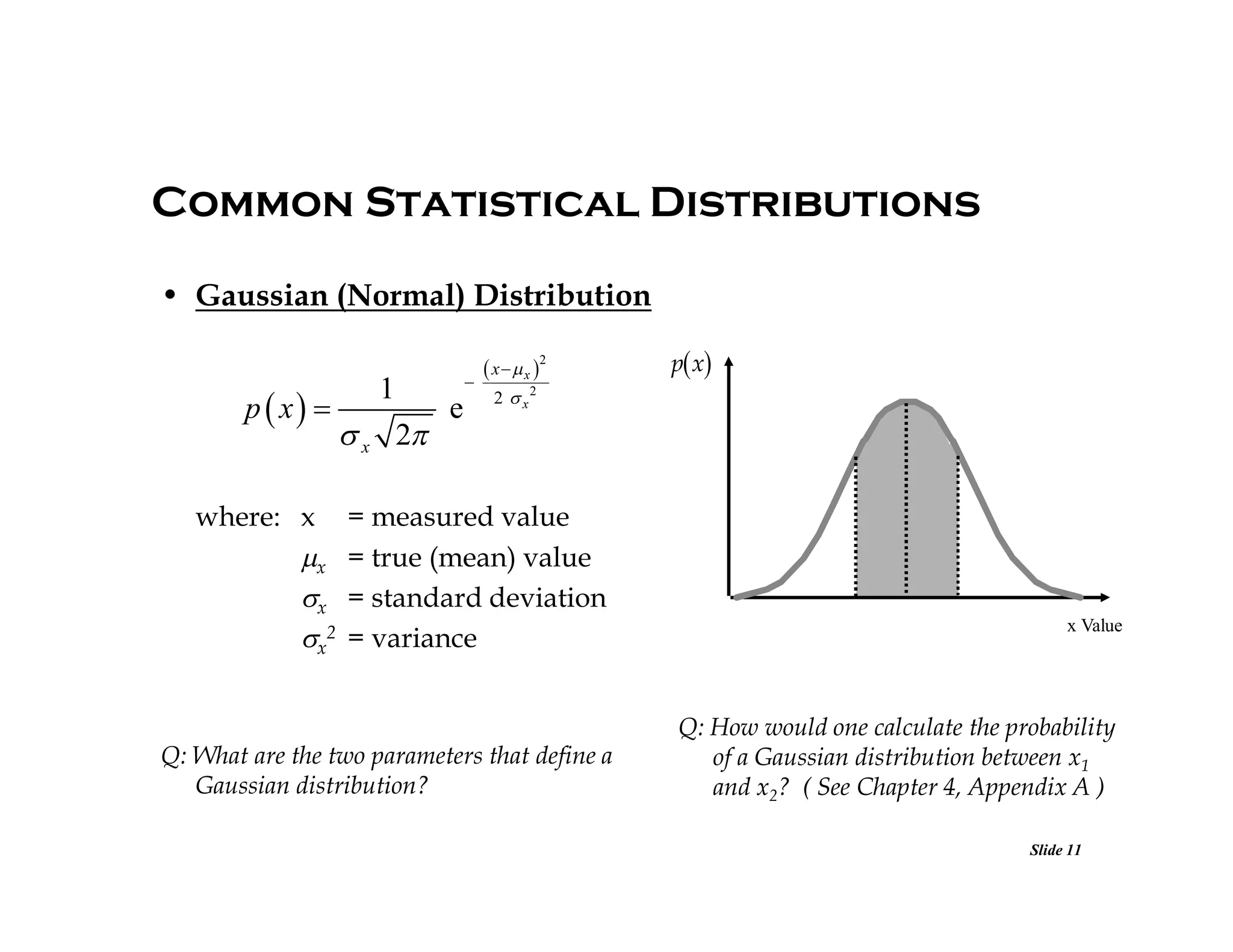
Ex: A voltage measurement has a Gaussian
distribution with mean 3.4 [V] and a
standard deviation of 0.4 [V]. Using
Chapter 4, Appendix A, calculate the
probability that a measurement is
between:
(a) [2.98, 3.82] [V]
Ex: The quantization error of an ADC has
a uniform distribution in the
quantization interval Q. What is the
probability that the actual input voltage
is within Q/8 of the estimated input
voltage?
(b) [2.4, 4.02] [V]
Slide 13

14. Statistical Analysis
• Standard Deviation (x and Sx )
– Characterize the typical deviation of measurements from the mean
and the width of the Gaussian distribution (bell curve).
– Smaller x , implies better ______________.
– Population Based
1
2

2
 x     x   x  p  x  dx
 



– Sample Based (N samples)
Sx 
1
N
N
 X
2
i
 x 
i 1
Q: Often we do not know x , how should we calculate Sx ?
Slide 14

15. Statistical Analysis
• Standard Deviation (x and Sx ) (cont.)
Common Name for
"Error" Level
Error Level in
Terms of 
% That the Deviation
from the Mean is Smaller
Odds That the
Deviation is Greater
Standard Deviation

68.3
about 1 in 3
"Two-Sigma Error"

95
1 in 20
"Three-Sigma Error"

99.7
1 in 370
"Four-Sigma Error"

99.994
1 in 16,000
 x  Z x  x   x  Z x
Slide 15

16. Statistical Analysis
• Sampled Mean x is the best estimate of x .

1 N
Best   x  E  X   
 Estimate
x p  x  dx
x   Xi

N i 1
Degree of Freedom
• Sampled Standard Deviation ( Sx )
– Use x when x is not available.  reduce by one degree of freedom.
Sx 
1
N
N
 X
i 1
2
i
 x 
N
1
2
     S x 

 X i  x 
N  1 i 1
When  x not known
Q: If the sampled mean is only an estimate of the “true mean” x , how do we characterize its
error?
Q: If we take another set of samples, will we get a different sampled mean?
Q: If we take many more sample sets, what will be the statistics of the set of sampled means?
Slide 16

17. Statistical Analysis
Ex: The inlet pressure of a steam generator was measured 100 times during a 12 hour
period. The specified inlet pressure is 4.00 MPa, with 0.7% allowable
fluctuation. The measured data is summarized in the following table:
Pressure (P)(MPa) Number of Results (m)
3.970
1
3.980
3
3.990
12
4.000
25
4.010
33
4.020
17
4.030
6
4.040
2
4.050
1
(1) Calculate the mean, variance and standard deviation.
(2) Given the data, what pressure range will contain 95% of the data?
Slide 17

18. Confidence Interval
• Sampled Mean Statistics
– If N is large, x will also have a Gaussian distribution. (Central Limit Theorem)
– Mean of x :
x  E x   x
x is an unbiased estimate.
p( x )
p( x )
– Standard Deviation of x :
x 
x
N
 x is the best estimate of the error
in estimating x .
p( x )
x

x
Q: Since we don’t know x , how would we calculate  x ?
Slide 18

19. Confidence Interval
• For Large Samples ( N > 60 ), Q% of all the sampled means x
will lie in the interval
p x 
x
x  z Q x  x  z Q
N
Equivalently,


x  zQ x  x  x  zQ x
N
N


x
x
is the Q% Confidence Interval
x
x
zQ x zQ x
When x is unknown, Sx will be a reasonable approximation.
Slide 19

20. Confidence Interval
Ex: 64 acceleration measurements were taken during an experiment. The
estimated mean and standard deviation of the measurements were 3.15 m/s2
and 0.4 m/s2.
(1) Find the 98% confidence interval for the true mean.
(2) How confident are you that the true mean will be in the range from 2.85
to 3.45 m/s2 ?
Slide 20

21. Confidence Interval
• For Small Samples ( N < 60 ), the Q% Confidence Interval can
be calculated using the Student-T distribution, which is
similar to the normal distribution but depends on N.
– with Q% confidence, the true mean x will lie in the
following interval about any sampled mean:
Sx
Sx
x  t  ,Q
 x  x  t  ,Q
 Q% confidence interval
N
N


Sx
Sx
where   N  1
t,Q is defined in class notes Chapter 4, Appendix B.
Slide 21

22. Confidence Interval
Ex: A simple postal scale is supplied with ½ , 1, 2, and 4 oz brass weights. For
quality check, 14 of the 1 oz weights were measured on a precision scale. The
results, in oz, are as follows:
1.08
1.03
0.96
0.95
1.04
1.01
0.98
0.99
1.05
1.08
0.97
1.00
0.98
1.01
Based on this sample and that the parent population of the weight is normally
distributed, what is the 95% confidence interval for the “true” weight of the 1 oz
brass weights?
Slide 22

23. Propagation of Error
Q: If you measured the diameter (D) and height (h) of a cylindrical
container, how would the measurement error affect your estimation of
the volume ( V = D2h/4 )?
Q: What is the uncertainty in calculating the kinetic energy ( mv2/ 2 )
given the uncertainties in the measurements of mass (m) and velocity
(v)?
How do errors propagate through calculations?
Slide 23

24. Propagation of Error
• A Simple Example
Suppose that y is related to two independent quantities X1 and
X2 through
y  C1 X 1  C 2 X 2  f  X 1 , X 2 
To relate the changes in y to the uncertainties in X1 and X2, we
need to find dy = g(dX1, dX2):
dy 
The magnitude of dy is the expected change in y due to the
uncertainties in x1 and x2:
2
2
 f
  f

 y  y  
x1   
x 2  
 X
  X

 1
  2

C    C  
2
1
x1
2
2
x2
Slide 24

25. Propagation of Error
• General Formula
Suppose that y is related to n independent measured variables
{X1, X2, …, Xn} by a functional representation:
y  f X 1, X 2 , , X n 
Given the uncertainties of X’s around some operating points:
x1  x 1 , x 2  x 2 , , x n  x n 
The expected value of y and its uncertainty y are:
y  f  x1 , x1 ,  , xn 
2
2
 f
  f

 f

y  
x1   
x2     
x n 
 X
  X

 X

 1
  2

 n

2
 x1 , x1 ,, x n 
Slide 25

26. Propagation of Error
•Proof:
Assume that the variability in measurement y is caused
by k independent zero-mean error sources: e1, e2, . . . , ek.
Then, (y - ytrue)2 = (e1 + e2 + . . . + ek)2
= e12 + e22 + . . . + ek2 + 2e1e2 + 2e1e3 + . . .
E[(y - ytrue)2] = E[e12 + e22 + . . . + ek2 + 2e1e2 + 2e1e3 + . . .]
= E[e12 + e22 + . . . + ek2]
y 
   
 
E e1 2  E e2 2    E e k 2   1 2   2 2     k 2
Slide 26

27. Propagation of Error
• Example (Standard Deviation of Sampled Mean)
Given
x 
1
X 1  X 2  X 3    X N
N

Use the general formula for error propagation:
2
x 
 x
  x

 x1   
 X
  X  x2
1
2

 
x 
2
2

 x
  x
 
 x3     
  X

 X  x N
3
N
 






2
x
N
Slide 27

28. Propagation of Error
Ex: What is the uncertainty in calculating the kinetic energy ( mv2/ 2 ) given
the uncertainties in the measurements of mass (m) and velocity (v)?
2
KE
KE 
KE  
m  
v



 m

 v

2
1 
m  2 
v  2
 mv 2
   2 mv 2 


2 
m
v
1
m  2  v  2

  2 
 mv 2 
 m
 v
2
Slide 28

29. • Best Linear Fit
–How do we characterize “BEST”?
Fit a linear model (relation)
Output Y
Least Squares Fitting of Data
best linear
fit yest

yi  ao  a1 xi
to N pairs of [xi, yi] measurements.
Given xi, the error between the

estimated output y i and the measured
output yi is:

ni  yi  yi
measured
output yi
Input X
The “BEST” fit is the model that
 N 2
N
2

 min   ni   min   yi  yi  
minimizes the sum of the ___________
 i=1   
i=1


of the error
Least Square Error
Slide 29

30. Least Squares Fitting of Data
N
N
2
2
Let

J     yi  yi      yi  ao  a1 x i 
 i=1
 i=1
The two independent variables are?
M inim ize J  Find a o and a1 such that dJ  0
J
J
 0 
 0 
 a
a o
N
   i  1 2  y i  a o  a1 x i   0
N
   i  1 2 x i  y i  a o  a1 x i   0
Q: What are we trying to solve?
Slide 30

31. Least Squares Fitting of Data
Rewrite the last two equations as two simultaneous equations for
ao and a1:
x 
y
a N  a
 i
1 i
 o

2
 a o  x i  a1  x i 

    x i yi 




  ao    yi 
  a     x y 
  1   i i 
  

 xi 2  yi    xi   xi yi 
ao 



N   xi yi    xi   yi 

a1 


  xi 2    xi 
where   N
Slide 31
2

32. Least Squares Fitting of Data
• Summary: Given N pairs of input/output measurements [xi, yi],
the best linear Least Squares model from input xi to output yi is:

yi  ao  a1 xi
  x  y    x   x y 

2
where
ao
a1 
i
i
i
i i

N   x i yi    x i  yi 
and   N
  
x i 2   xi 

• The process of minimizing squared error can be used for fitting
nonlinear models and many engineering applications.
• Same result can also be derived from a probability distribution
point of view (see Course Notes, Ch. 4 - Maximum Likelihood Estimation ).
Q: Given a theoretical model y = ao + a2 x2 , what are the Least Squares estimates for ao & a2?
Slide 32
2

33. Least Squares Fitting of Data
• Variance of the fit:

n2 
1
N 2
 yi  ao  a1xi 2

N
i 1
• Variance of the measurements in y: y2
• Assume measurements in x are precise.
• Correlation coefficient:

 n2
n2
R 1 2 1 2 ,
y
Sy
2
is a measure of how well the model explains the data.
R2 = 1 implies that the linear model fits the data perfectly.
Slide 33