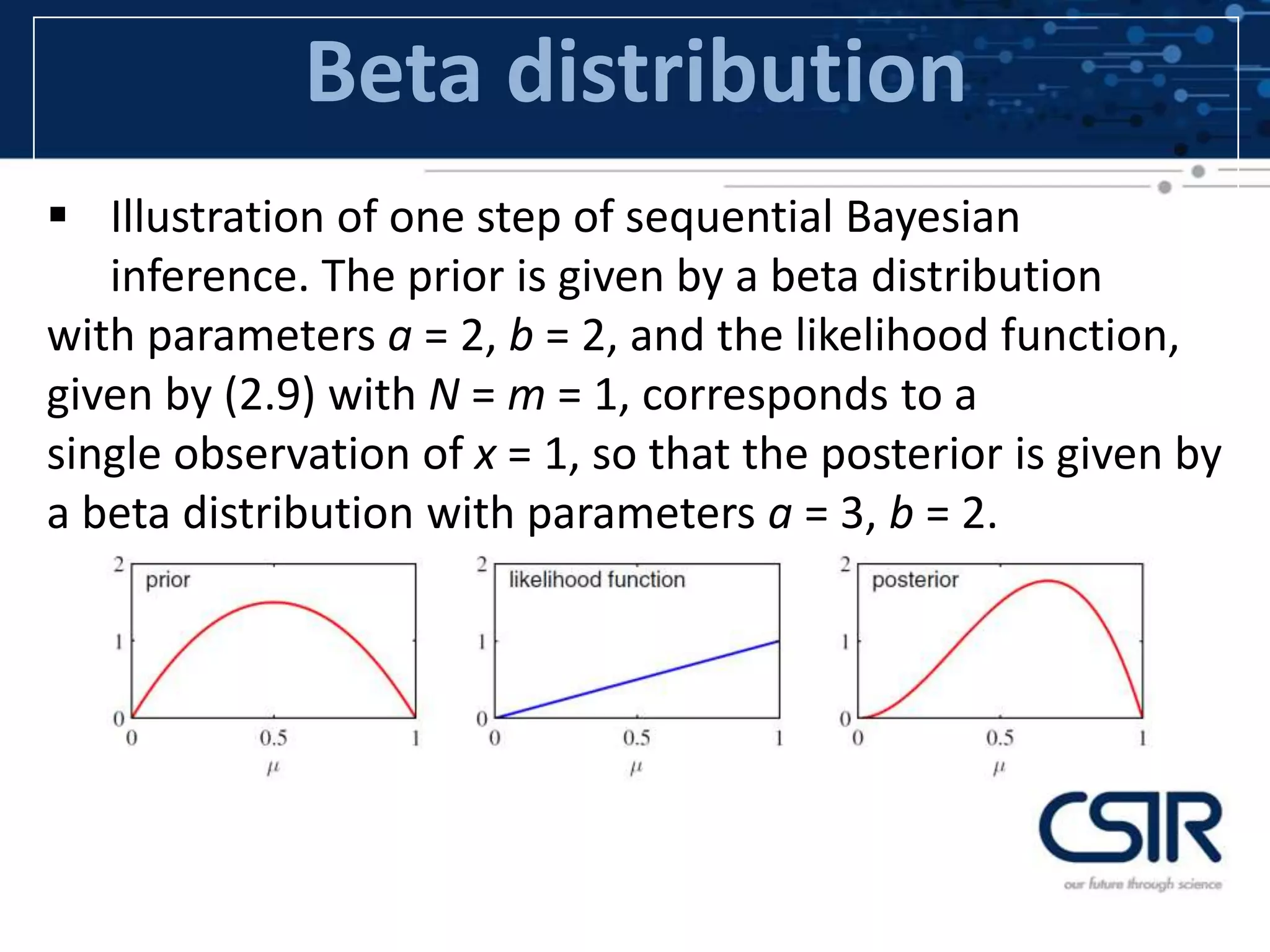
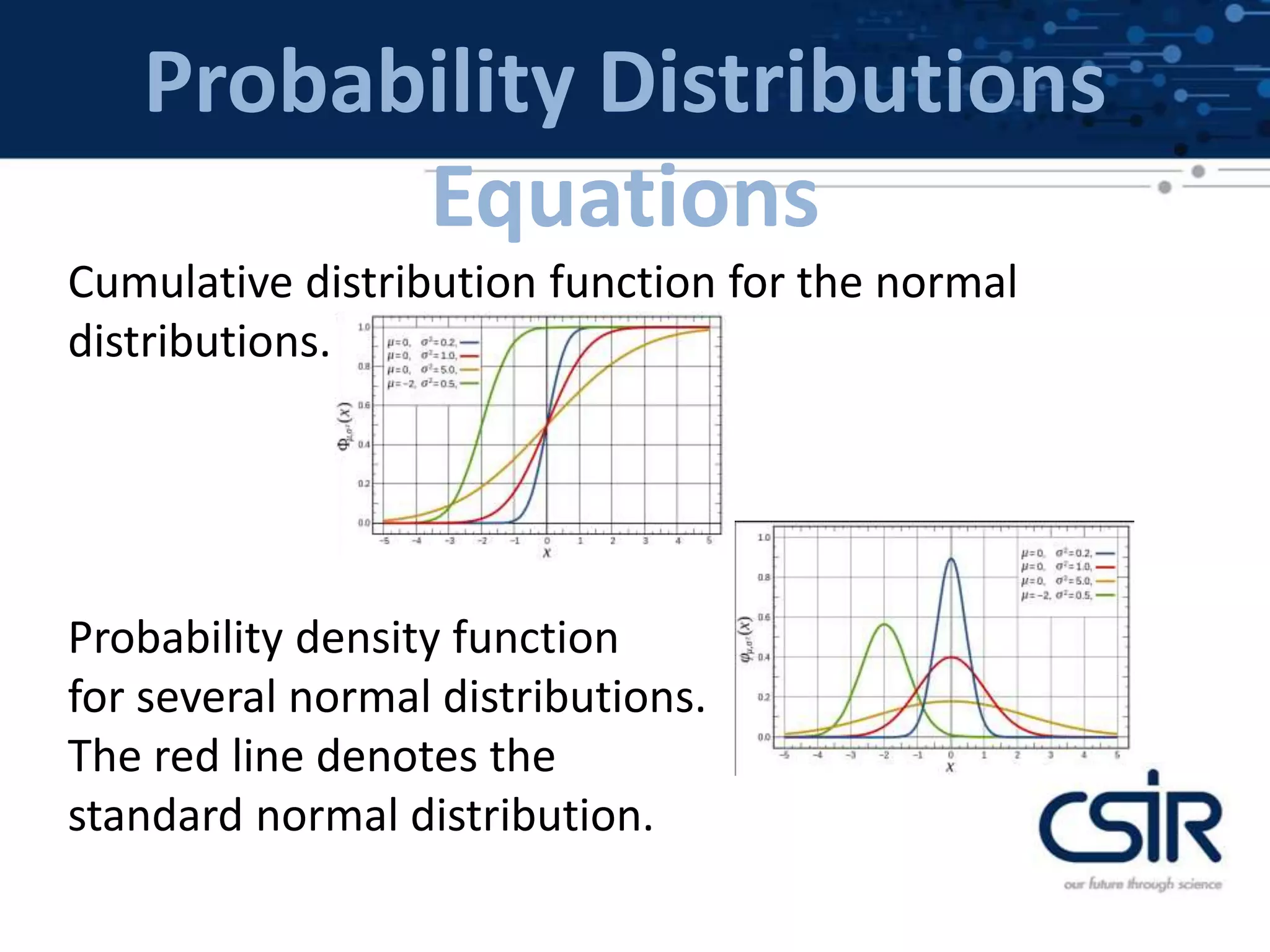
This document provides an overview of probability distributions and related concepts. It defines key probability distributions like the binomial, beta, multinomial, and Dirichlet distributions. It also describes probability distribution equations like the cumulative distribution function and probability density function. Additionally, it outlines descriptive parameters for distributions like mean, variance, skewness and kurtosis. Finally, it briefly discusses probability theorems such as the law of large numbers, central limit theorem, and Bayes' theorem.

1. Beatrice van Eden
Probability Distribution
Part 1

2. Topics
 Probability Distribution
 Probability Distribution Equations
 Descriptive parameters for Probability Distributions
 Probability Theorems
 Binary Variables
 The beta distribution
 Multinomial Variables
 The Dirichlet distribution

3. Probability Distribution
A function that describes all the possible values and
likelihoods that a random variable can take within a
given range.
This range will be between the minimum and
maximum possible values, but where the possible
value is likely to be plotted on the probability
distribution depends on a number of factors, including
the distributions mean, standard deviation, skewness
and kurtosis.

4. Probability Distributions
Equations
The section on probability equations explains the
equations that define probability distributions.
Cumulative distribution function (cdf)
Probability mass function (pmf)
Probability density function (pdf)

5. Probability Distributions
Equations
Cumulative distribution function (cdf)
The (cumulative) distribution function, or probability
distribution function, F(x) is the mathematical equation
that describes the probability that a variable X is less
that or equal to x, i.e.
F(x) = P(X≤x) for all x
where P(X≤x) means the probability of the event X≤x.

6. Probability Distributions
Equations
Cumulative distribution function for the normal
distributions.
Probability density function
for several normal distributions.
The red line denotes the
standard normal distribution.

7. Probability Distributions
Equations
A cumulative distribution function has the following
properties:
 F(x) is always non-decreasing, i.e.
 F(x) = 0 at x = -∞ or minimum
F(x) = 1 at x = ∞ or maximum
( ) 0
d
F x
dx


8. Probability Distributions
Equations
Probability mass function (pmf)
If a random variable X is discrete, i.e. it may take any of
a specific set of n values xi, i = 1 to n, then:
P(X=xi) = p(xi)
p(x) is called the probability mass function

9. Probability Distributions
Equations
 The graph of a probability mass function. All the
values of this function must be non-negative and
sum up to 1.
 The probability mass function of a fair die. All the
numbers on the die have an equal chance of
appearing on top when the die stops rolling.
1 3 7
0.2 0.5 0.3
1 2 3 4 5 6
1/6 1/6 1/6 1/6 1/6 1/6

10. Probability Distributions
Equations
Note that
and F(xk) =
1
( ) 1
n
i
i
p x


1
( )
k
i
i
p x



11. Probability Distributions
Equations
Probability density function (pdf)
If a random variable X is continuous, i.e. it may take any
value within a defined range (or sometimes ranges),
the probability of X having any precise value within that
range is vanishingly small because a total probability of
1 must be distributed between an infinite number of
values. In other words, there is no probability mass
associated with any specific allowable value of X.

12. Probability Distributions
Equations
Instead, we define a probability density function f(x) as:
i.e. f(x) is the rate of change (the gradient) of the
cumulative distribution function. Since F(x) is always
non-decreasing, f(x) is always non-negative.
( ) ( )
d
f x F x
dx


13. Probability Distributions
Equations
For a continuous distribution we cannot define the
probability of observing any exact value. However, we
can determine the probability of lying between any two
exact values (a, b):
where b>a.
( ) ( ) ( )P a x b F b F a   

14. Descriptive parameters for
Probability Distributions
The section on probability parameters explains the
meaning of standard statistics like mean and variance
within the context of probability distributions.

15. Descriptive parameters for
Probability Distributions
Location
Mode: is the x-value with the greatest
probability p(x) for a discrete distribution, or the
greatest probability density f(x) for a continuous
distribution.
Median: is the value that the variable has a 50%
probability of exceeding, i.e. F(x50) = 0.5

16. Descriptive parameters for
Probability Distributions
Mean : also known as the expected value, is
given by:
for discrete variables
for continuous variables
The mean is known as the first moment about zero. It
can be considered to be the centre of gravity of the
distribution.
1
n
i i
i
x p

 
. ( ).x f x dx


 

17. Descriptive parameters for
Probability Distributions
Spread
Standard Deviation: measures the amount of
variation or dispersion from the average or mean. The
standard deviation is the positive square root of the
variance.
The standard deviation has the same dimension as the
data, and hence is comparable with deviations of the
mean.

18. Descriptive parameters for
Probability Distributions
Variance: measures how far a set of numbers is
spread out.
An equivalent measure is the square root of the
variance, called the standard deviation.
The variance is one of several descriptors of
a probability distribution. In particular, the variance is
one of the moments of a distribution.

19. Descriptive parameters for
Probability Distributions
Shape
Skewness:
The skewness statistic is calculated from the following
formulae:
Discrete variable:
Continuous variable:
max
3
min
3
( ) . ( ).x f x dx
S





3
1
3
( ) .
n
i i
i
x p
S







20. Descriptive parameters for
Probability Distributions
Kurtosis:
The kurtosis statistic is calculated from the following
formulae:
Discrete variable:
Continuous variable:
max
4
min
4
( ) . ( ).x f x dx
K





4
1
4
( ) .
n
i i
i
x p
K







21. Probability Theorems
Probability theorems explains some fundamental
probability theorems most often used in modelling risk,
and some other mathematical concepts that help us
manipulate and explore probabilistic problems.
 The strong law of large numbers
 Central limit theorem
 Binomial Theorem
 Bayes theorem

22. Probability Theorems
 The strong law of large numbers
 The strong law of large numbers says that the larger
the sample size (i.e. the greater the number of
iterations), the closer their distribution (i.e. the risk
analysis output) will be to the theoretical
distribution (i.e. the exact distribution of the models
output if it could be mathematically derived).

23. Probability Theorems
 Central Limit Theorem(CLT)
The distribution of the sum of N i.i.d. random
variables becomes increasingly Gaussian as N
grows.
Example: N uniform [0,1] random variables.

24. Probability Theorems
 Binomial Theorem
a Formula for finding any power of a binomial without
multiplying at length.
Properties of binomial coefficient!
!( )!
n n
x x n x

 
 
 
0
1
1
0
n
i
n n
n x x
n n n
x x n x
n n
n
a b a b
n b n i


   
   
   
     
     
     
   
    
   
    
    
    


25. Probability Theorems
 Bayes theorem
a theorem describing how the conditional probability
of each of a set of possible causes for a given observed
outcome can be computed from knowledge of the
probability of each cause and the conditional
probability of the outcome of each cause.

26. Topics
 Binary Variables
 The beta distribution
 Multinomial Variables
 The Dirichlet distribution

27. Binary Variables
Binary variable Observations (i.e., dependent variables)
that occur in one of two possible states,
often labelled zero and one. E.g., “improved/not
improved” and “completed
task/failed to complete task.”
 Coin flipping: heads=1, tails=0
 Bernoulli Distribution
( 1| )p x   
 
   
1
( | ) (1 )
var 1
x x
Bern x
x
x
  

 

 
 
 

28. Binary Variables
N coin flips
Binomial distribution
( | , )p m heads N 
 
0
2
0
( | , ) ( ) (1 )
( | , )
var[ ] ( [ ]) ( | , ) (1 )
m N m
m
N
m
N
m
Bin m N N
m mBin m N N
m m m Bin m N N
  
 
  



 
  
    



29. Beta distribution
Beta is a continuous distribution defined on the interval
of 0 and 1, i.e.,
parameterized by two positive parameters a and b.
where T(*) is gamma function. beta is conjugate to the
binomial and Bernoulli distributions
 0,1 
 
 
   
 
 
   
11
2
| , 1
var
1
ba
Beta
a b
a b
a b
a
a b
ab
a b a b
  


 
 
 
 
   

  

30. Beta distribution
 Illustration of one step of sequential Bayesian
inference. The prior is given by a beta distribution
with parameters a = 2, b = 2, and the likelihood function,
given by (2.9) with N = m = 1, corresponds to a
single observation of x = 1, so that the posterior is given by
a beta distribution with parameters a = 3, b = 2.

31. Beta distribution
Example
Beta1.odt

32. Multinomial Distribution
Multinomial distribution is a generalization of the
binominal distribution. Different from the binominal
distribution, where the RV assumes two outcomes, the RV
for multi-nominal distribution can assume k (k>2) possible
outcomes.
Let N be the total number of independent trials, mi,
i=1,2, ..k, be the number of times outcome i appears.
Then, performing N independent trials, the probability
that outcome 1 appears m1, outcome 2, appears m2,
…,outcome k appears mk times is

33. Multinomial Distribution
 
 
   
1 2
11 2
, ,...., | ,
...
var 1
cov
K
mK
K K
KK
K K
K K
j K j K
Mult
N
m m m N
m m m
m N
m N
m m N
 

 
 

 
  
 
 
 
    


34. The Dirichlet Distribution
The Dirichlet distribution is a continuous multivariate
probability distributions parametrized by a vector of
positive reals a. It is the multivariate generalization of the
beta distribution.
Conjugate prior for the
multinomial distribution.
 
   
10
11
1
( | )
...
0
K
K
k
kK
K
k
k
Dir 
 


 
 





 


