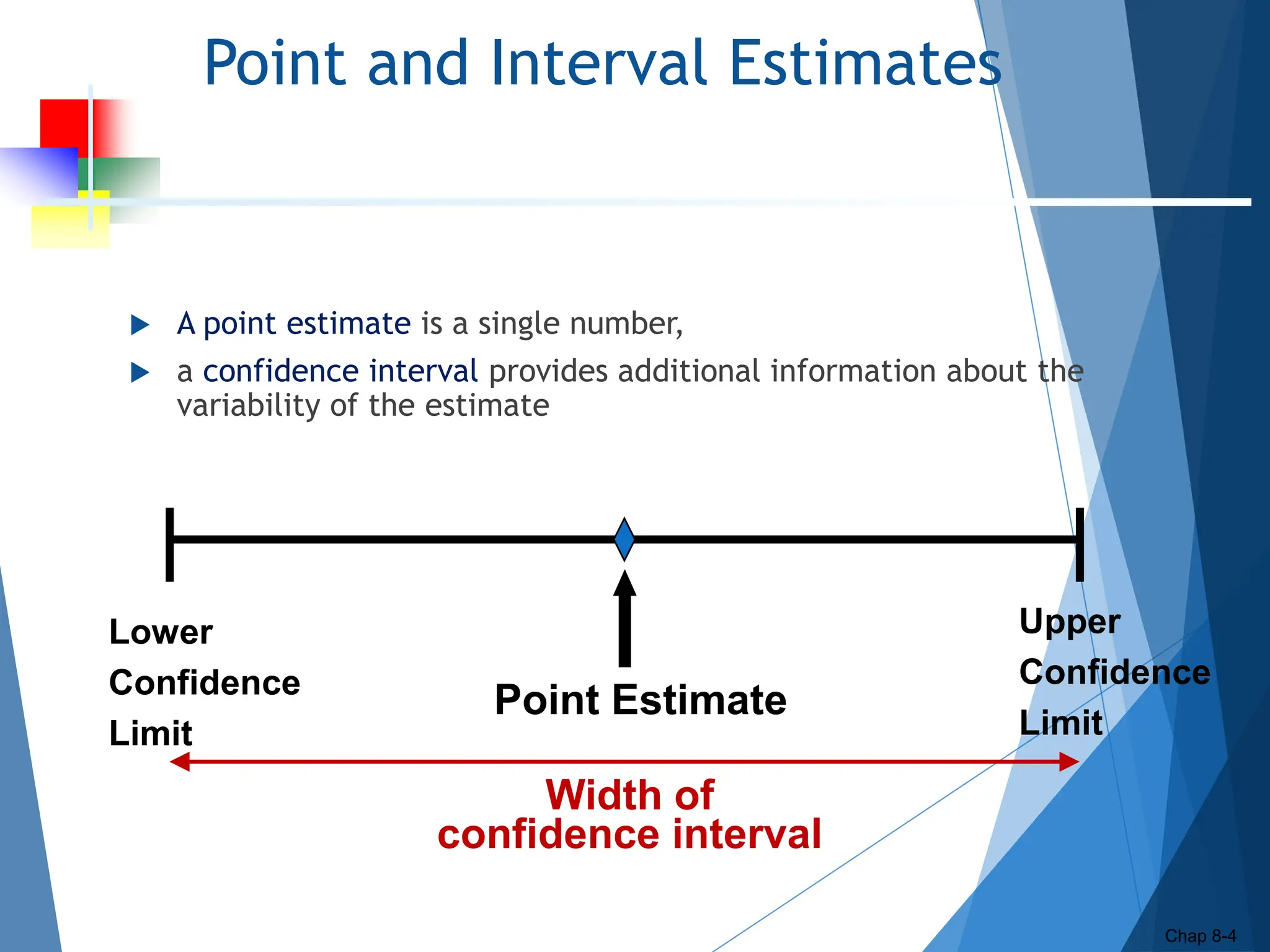
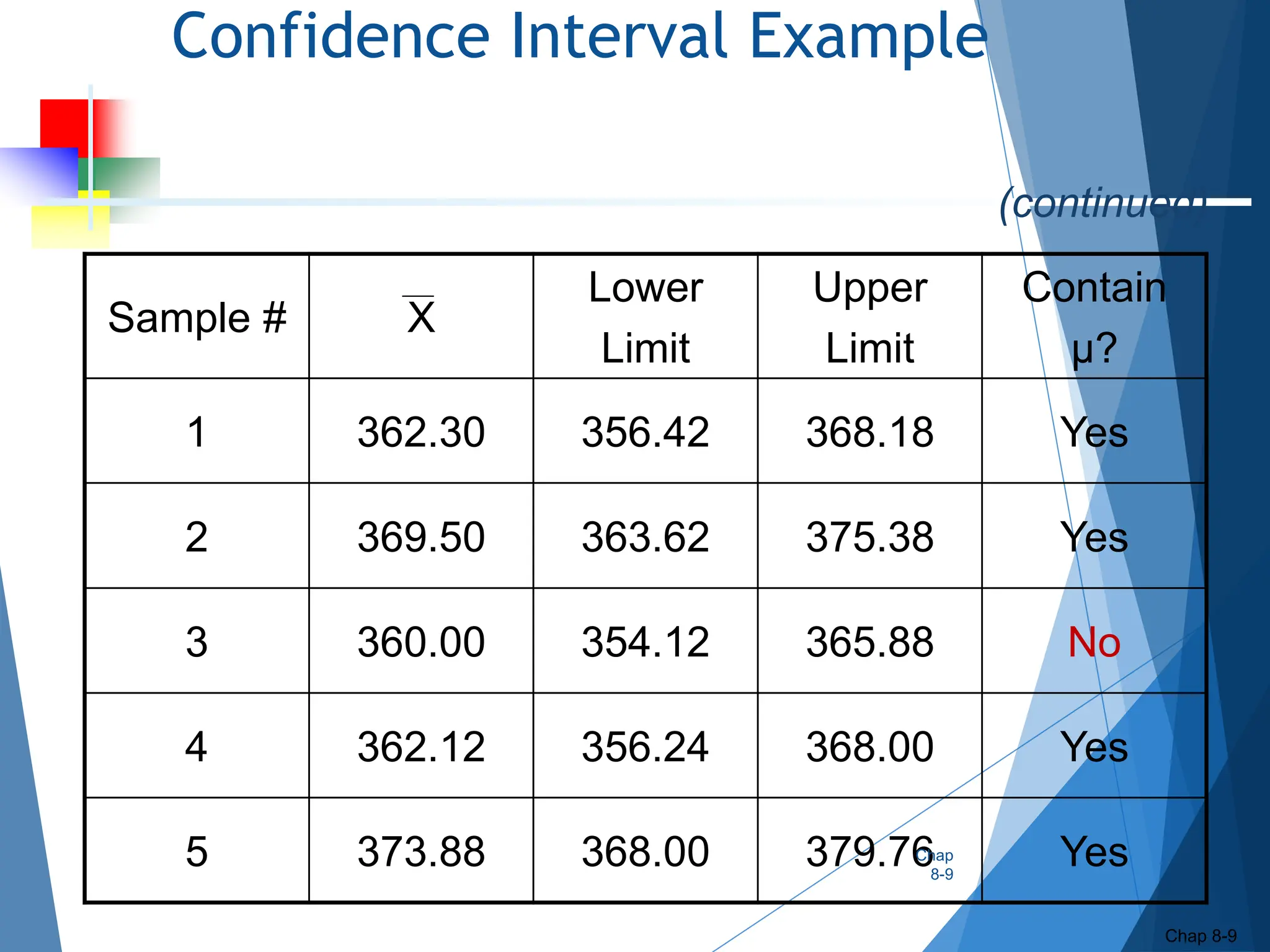
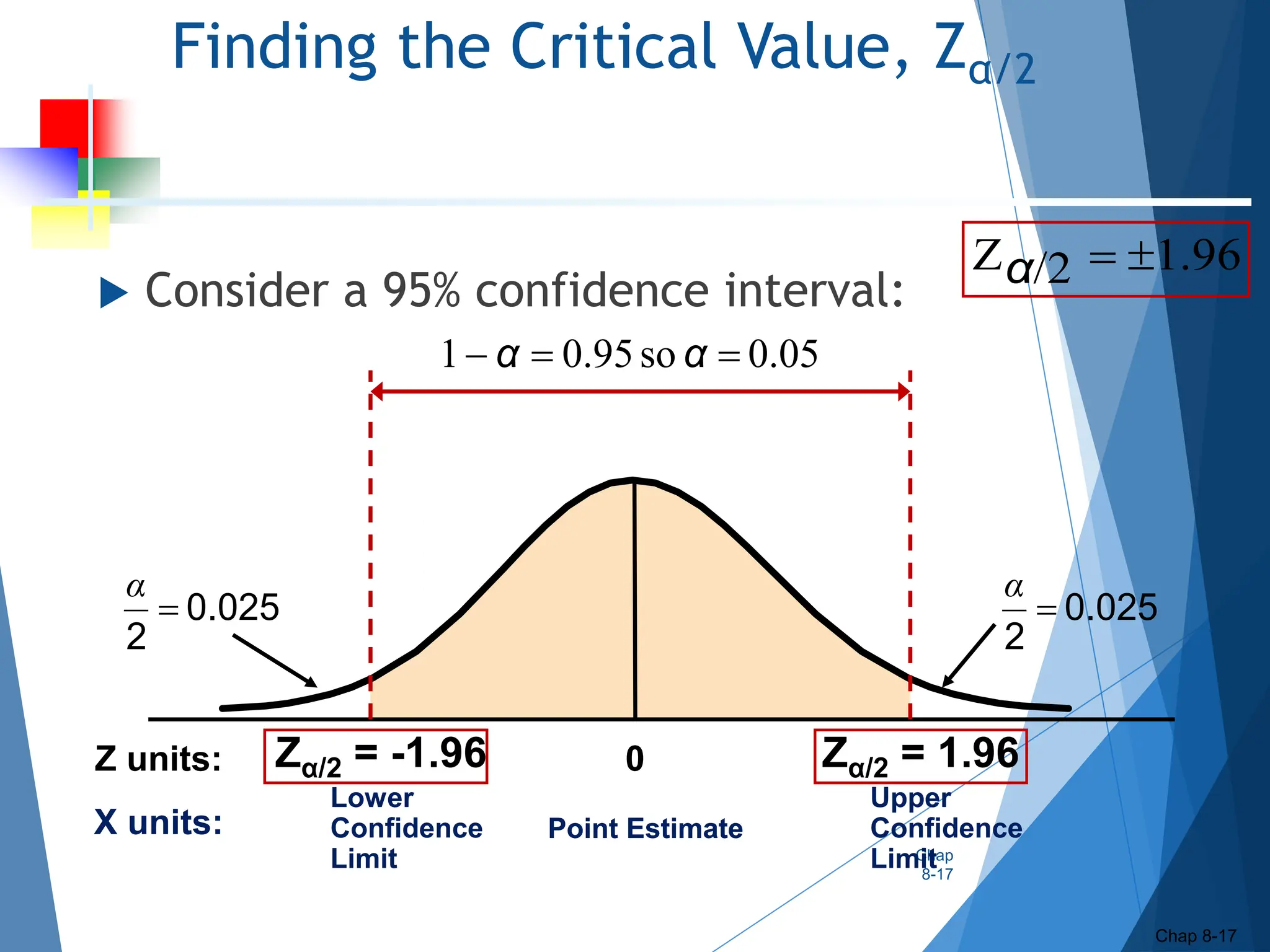
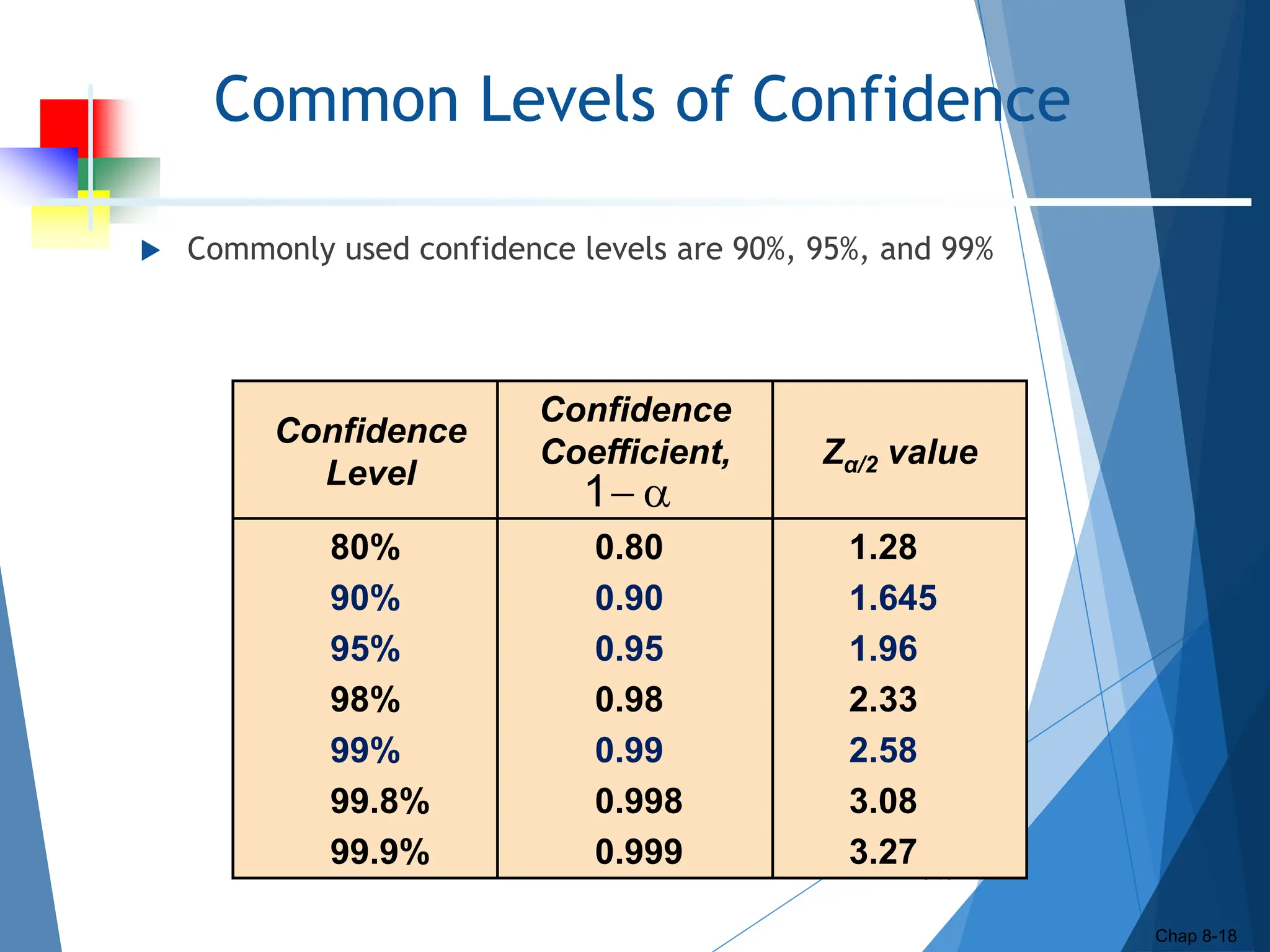
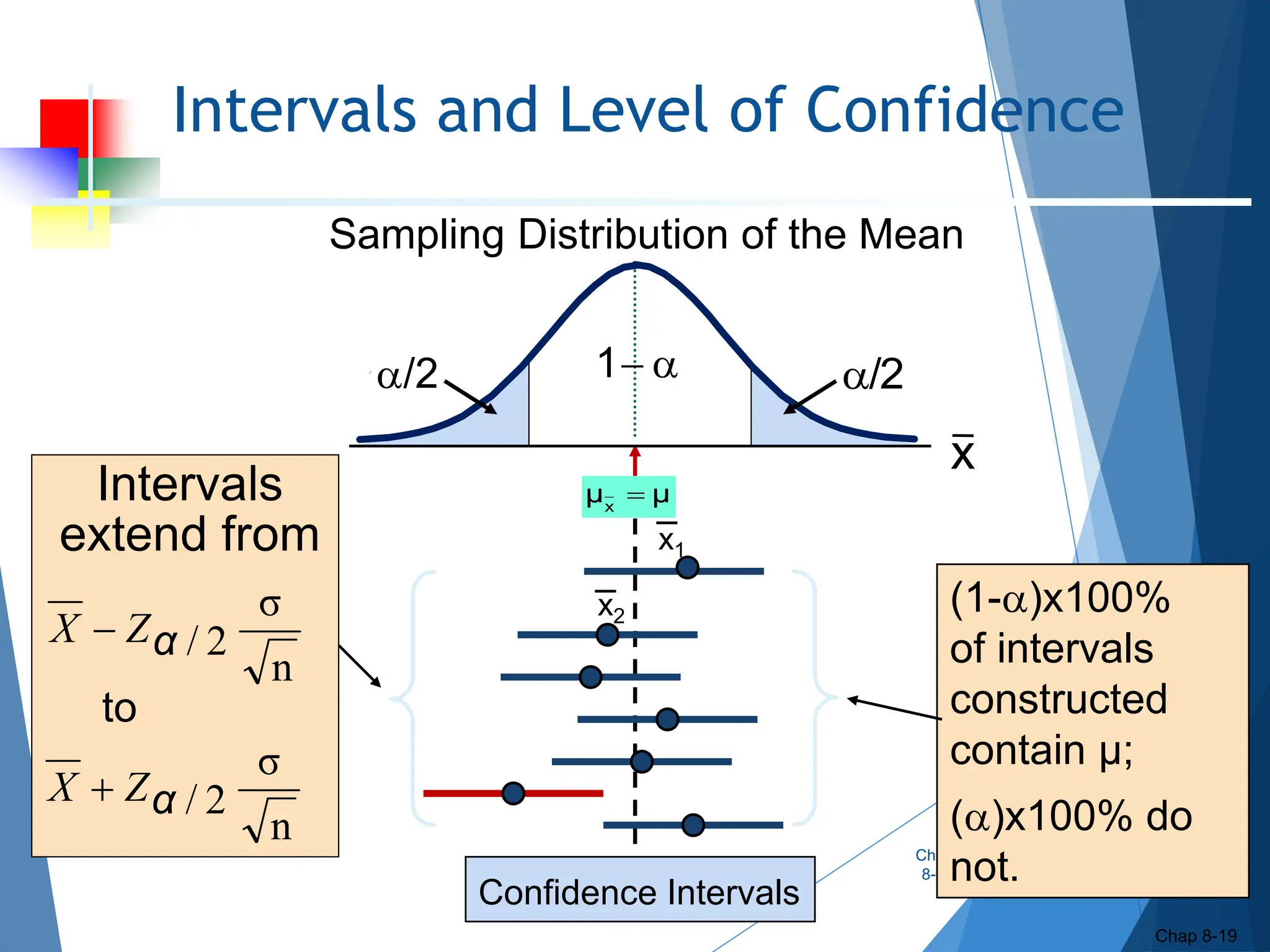
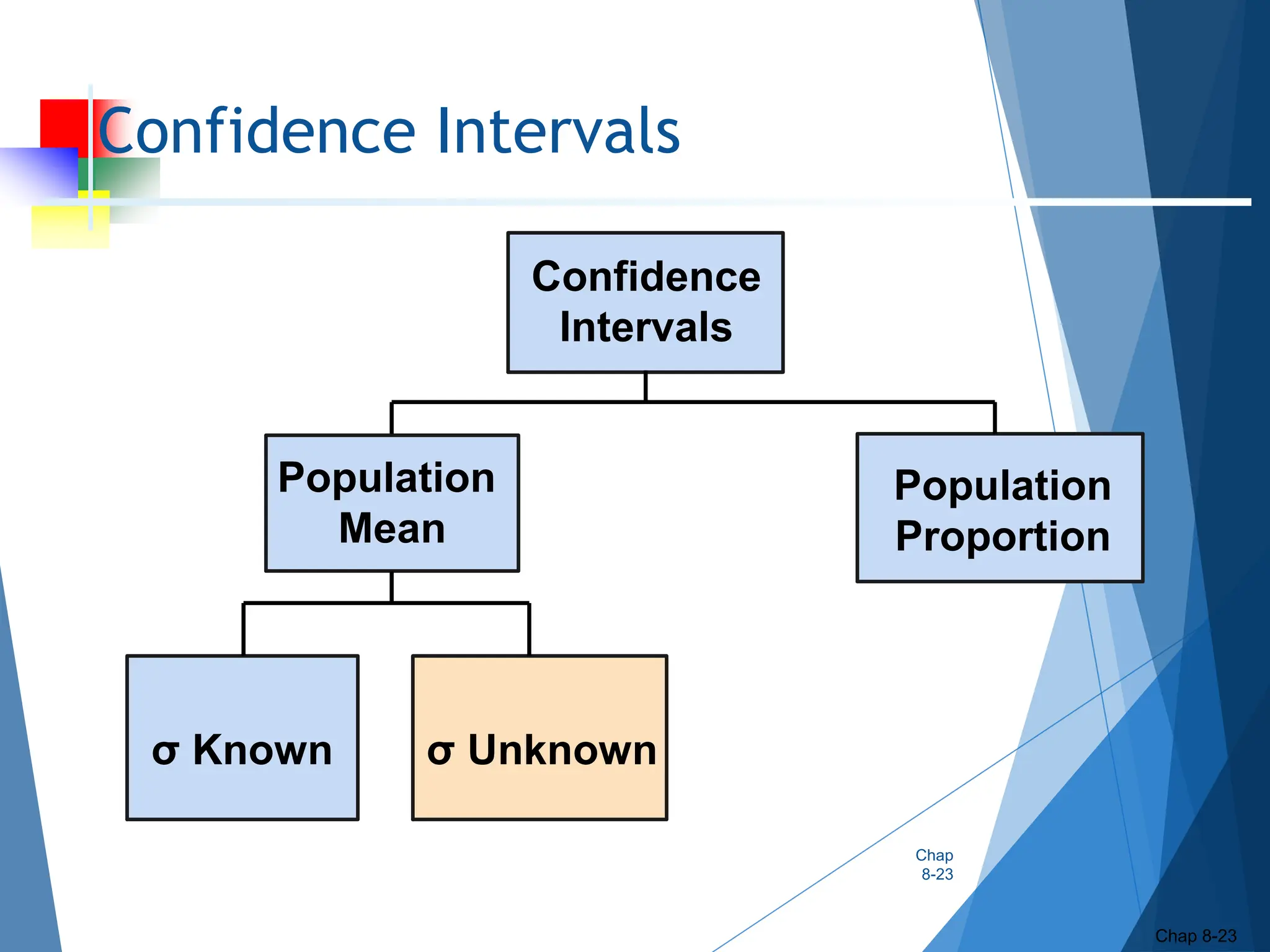
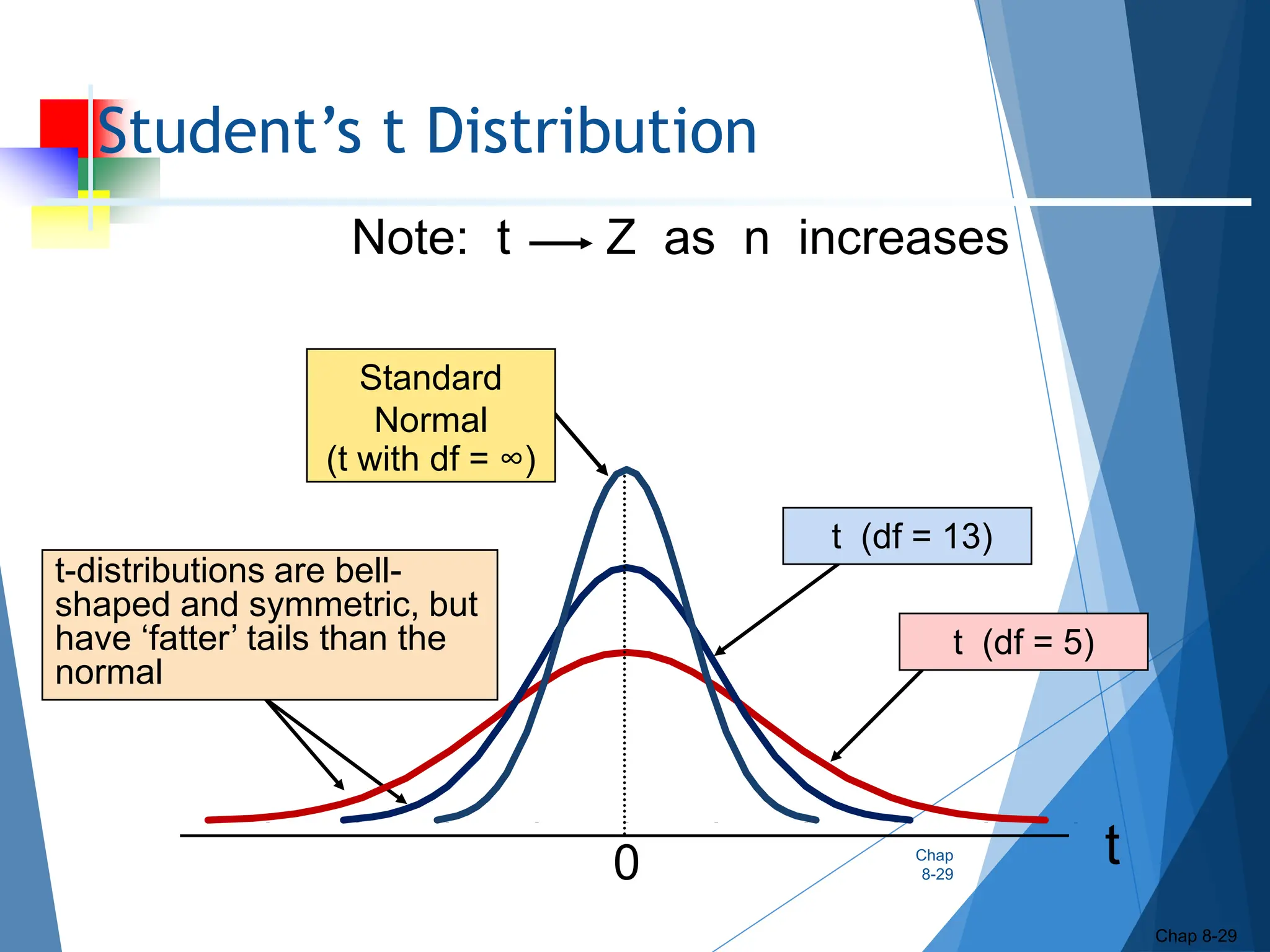
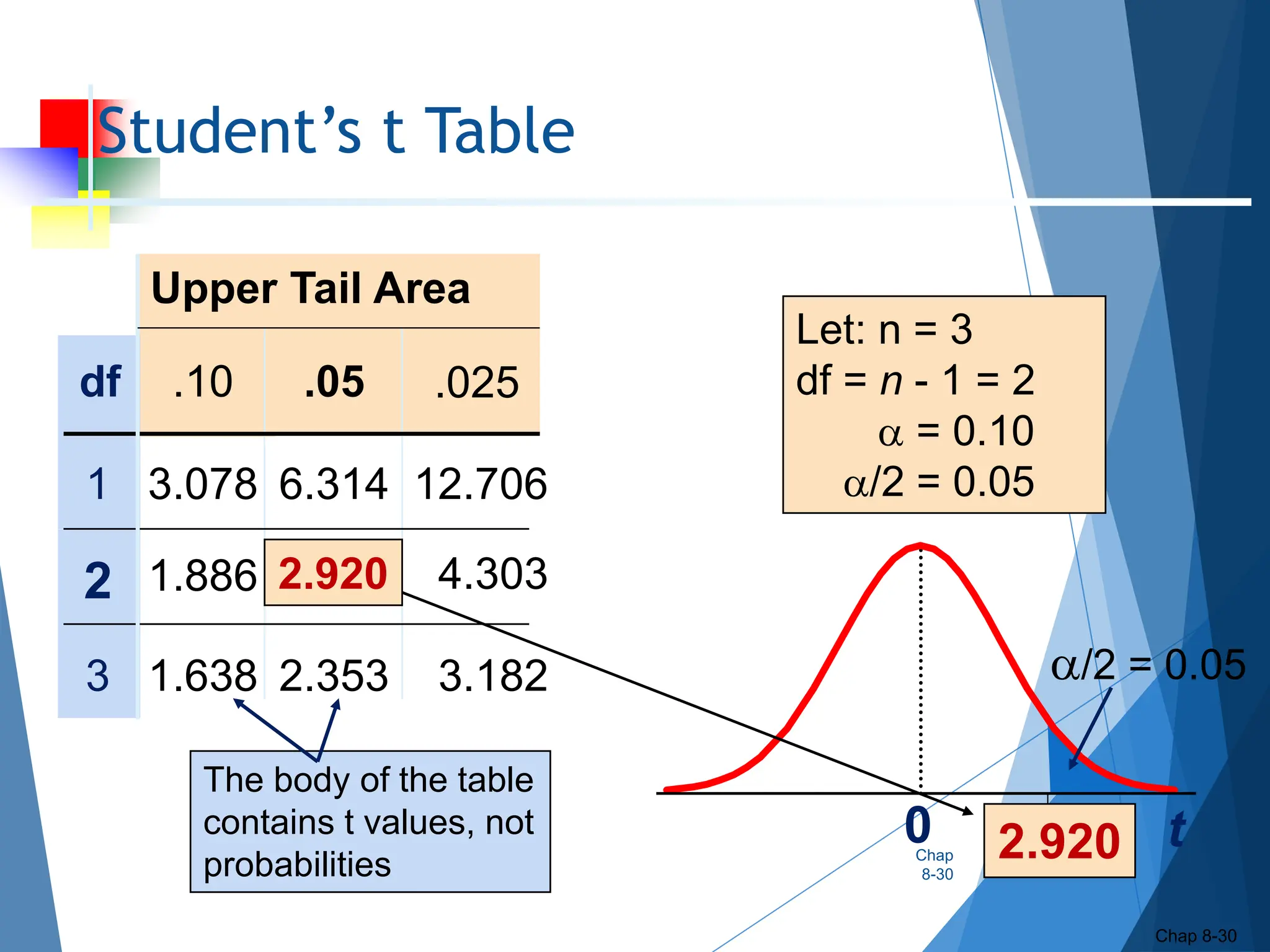
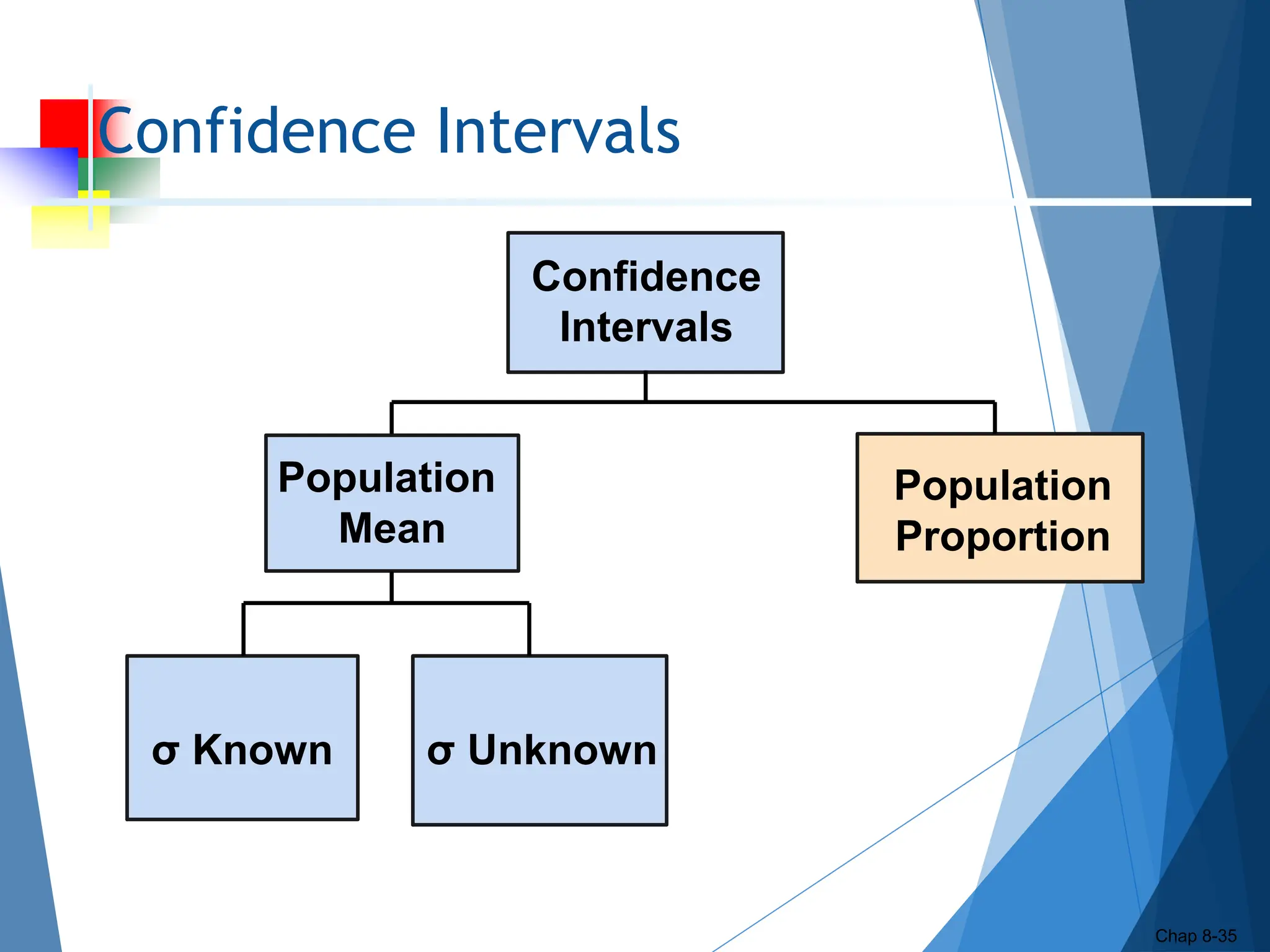
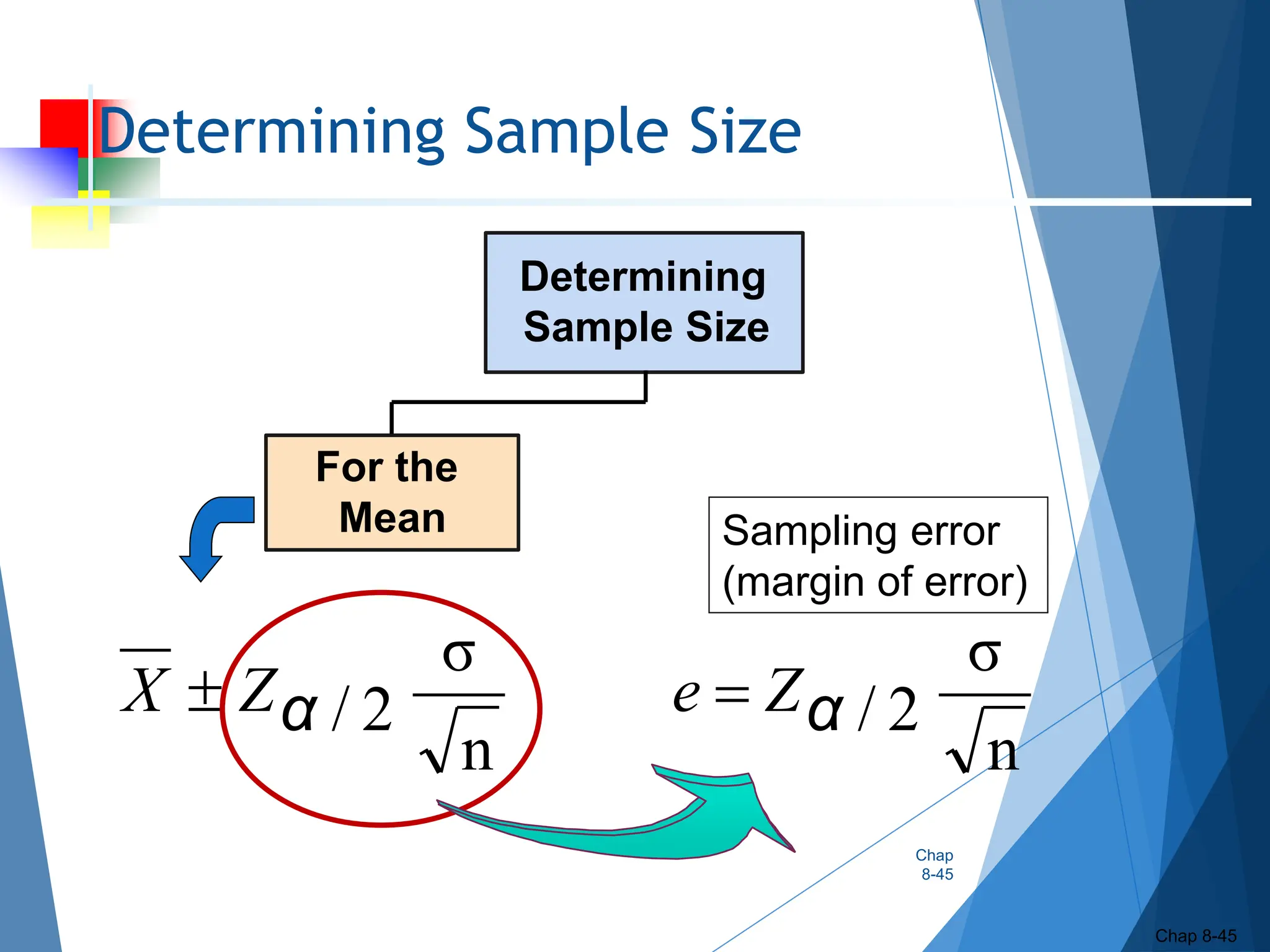
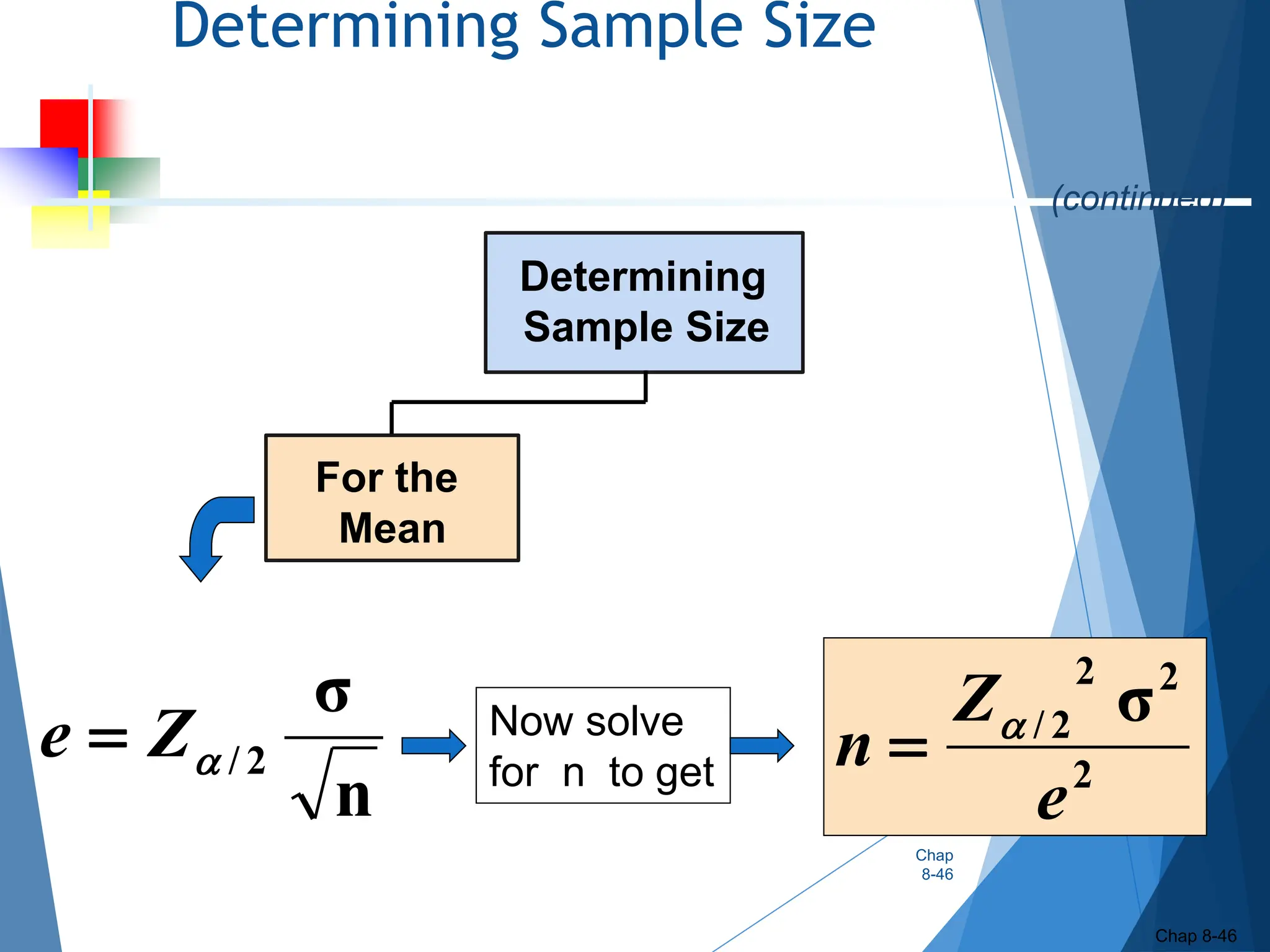
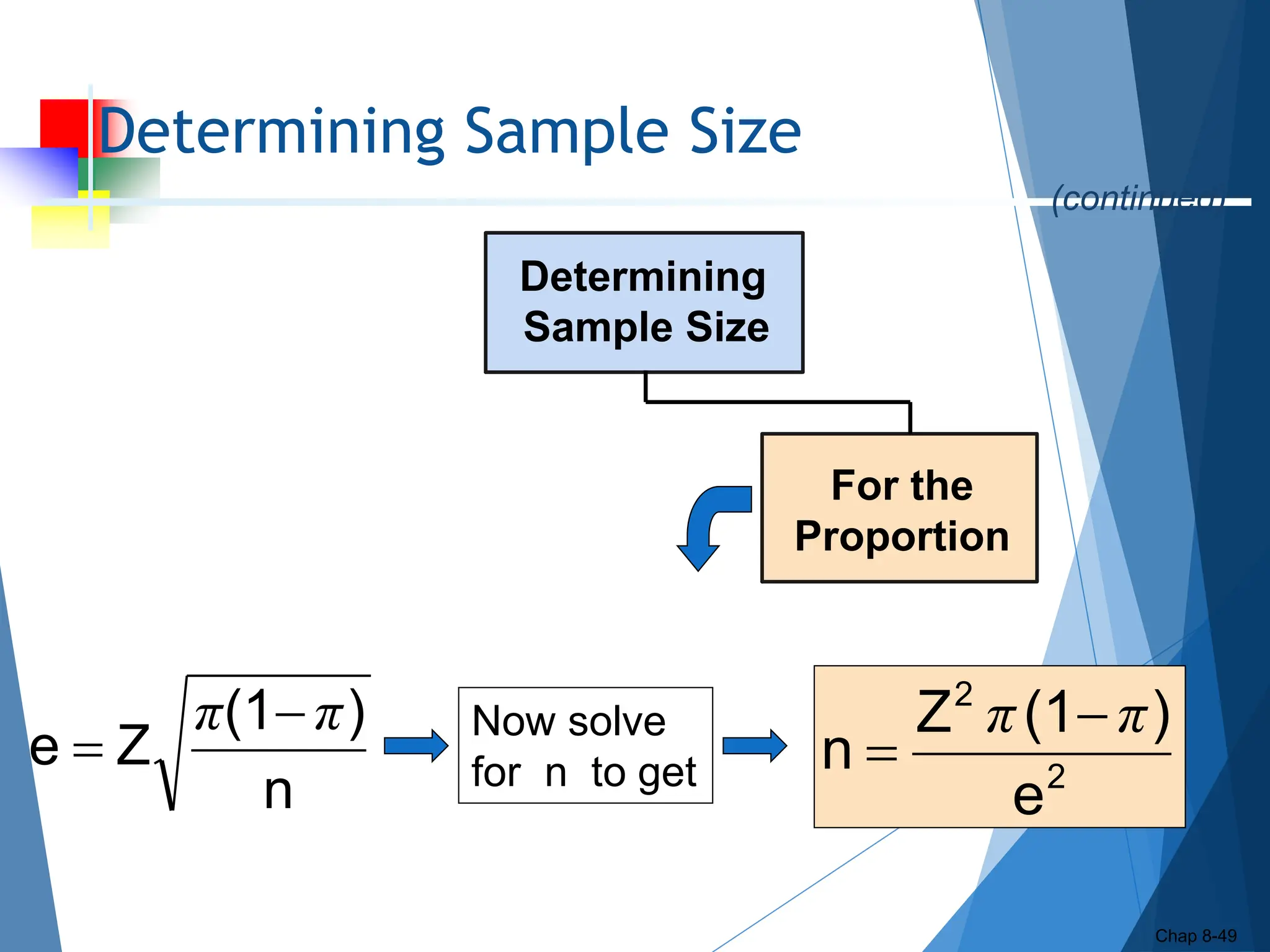
This document outlines key concepts related to constructing confidence intervals for estimating population means and proportions. It discusses how to calculate confidence intervals when the population standard deviation is known or unknown. Specifically, it provides the formulas and assumptions for constructing confidence intervals for a population mean using the normal and t-distributions. It also outlines how to calculate confidence intervals for a population proportion using the normal approximation. Examples are provided to demonstrate how to construct 95% confidence intervals for a mean and proportion based on sample data.