This document provides procedures for estimating precision error and determining confidence intervals of measurement means and differences between data sets. It begins by explaining how to calculate a confidence interval of the mean using the central limit theorem when sample size is large (>30), which gives a Gaussian distribution of mean values. When sample size is small (<30), it recommends using the Student's t-distribution. Examples are given of calculating confidence intervals at 95% probability levels. The document also covers the Student's t-test for determining if two data sets are significantly different based on calculating the t-value and comparing to t-distribution tables. In general, it advises using a 95% probability level for uncertainty calculations.

1. Question: How do we estimate precision error?

2. Histogram

3. Procedure
1. Find Xmax and Xmin from data
2. Determine # of interval K
1
)
1
(
87
.
1 4
.
0
+
−
= N
K
3. Estimate bin size Δx
2
2
x
x
x
x
x
Δ
+
<
≤
Δ
−
4. Find number of occurrence nj of
the data in each bin
5. Plot nj versus x
Histogram

4. Histogram

5. dx
x
p
b
x
a
P
b
a
∫
=
<
< )
(
)
(
1
)
(
)
( =
=
∞
<
<
−∞ ∫
∞
∞
−
dx
x
P
x
P
a b
∫
∞
∞
−
=
>=
< dx
x
xp
x
x )
(
Mean
∫
∞
∞
−
>
<
−
>
=<
−
= 2
2
2
2
)
(
)
( x
x
d
x
p
x
x
x
σ
Variance
x
σ
Standard derivation
Probability density function

6. Gaussian distribution
Variation due to random error
Some important distributions
Poisson distribution
Events occurring in time; p(x) refer to
probability of observing x events in time t
Bimodal distribution
???

7. Poisson distribution
• Poisson distribution is a discrete distribution
• e is the base of the natural logarithm (e = 2.71828...)
• k is the occurrence and k! is the factorial of k,
• λ is a positive real number, equal to the expected number of occurrences
that occur during the given interval. For instance, if the events occur on
average every 4 minutes, and you are interested in the number of events
occurring in a 10 minute interval, you would use as model a Poisson
distribution with λ = 10/4 = 2.5.
!
)
;
(
k
e
k
f
k
λ
λ
λ
−
=
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0 5 10 15 20
1
2
5
10
K
Probability

8. If only 2.5 students, on average, get an “A” in Dr. Wong’s
class, what is the chance of having 5 students getting “A” this
year? What about 0?
!
)
;
(
k
e
k
f
k
λ
λ
λ
−
=
Example
?
)
5
.
2
;
5
( =
f

9. Poisson distribution
!
)
;
(
k
e
k
f
k
λ
λ
λ
−
=
0
0.05
0.1
0.15
0.2
0.25
0.3
0 5 10
K
Probability

10. dx
e
dx
x
p
b
x
a
P
b
a
x
x
b
a
∫
∫
−
−
=
=
<
<
2
2
2
)
(
2
1
)
(
)
( σ
π
σ
2
2
2
)
(
2
1
)
( σ
π
σ
x
x
e
x
p
−
−
=
1
2
1
)
(
2
2
2
)
(
=
=
∞
<
<
−∞ ∫
∞
∞
−
−
−
dx
e
x
P
x
x
σ
π
σ
Gaussian distribution
A Gaussian distribution can be described by a mean and a
standard deviation σ
x

11. Normalized Gaussian Distribution
σ
β
σ
β
dx
d
x
x
=
−
= 2
2
2
)
(
2
1
)
( σ
π
σ
x
x
e
x
p
−
−
=
Note
β
π
β
β
d
e
z
z
p ∫
−
=
<
<
− 2
1
1
2
2
1
)
(
Consider
Normalized Gaussian distribution

13. E.g. Probability of a measurement with yield a value
within
σ
±
x
)
( σ
σ +
<
<
− x
x
x
P
)
1
1
( <
−
<
−
σ
x
x
P
3413
.
0
)
1
0
( =
<
≤ z
P
6826
.
0
2
3413
.
0
)
1
1
( =
×
=
<
≤
− z
P

14. Note:
9545
.
0
)
2
2
( =
+
<
≤
− σ
σ x
x
x
P
9973
.
0
)
3
3
( =
+
<
≤
− σ
σ x
x
x
P
-4 -3 -2 -1 1 2 3 4
0.1
0.2
0.3

15. IQ test scare are Gaussian distributed with a mean with 100 & a
standard deviation of 20
a) If you score 115, what percent of the population score below you?
b) What would you need to score to place you in 99th percentile (i.e. 99%
of the population scores below you)?

16. Statistical measurement theory
Measured values: X1, X2, X3, X4, X5, … XN
Sx
σ
X’
Sample measurement
Population
x
We want to estimate
x
u
x
x ±
=
'
ux is the uncertainty or confidence interval at some probability level P%
(P%)
x
x u
x
x
u
x −
≤
≤
− '

17. Statistical measurement theory
∑
=
+
+
+
+
=
=
N
i
N
i
N
x
x
x
x
N
x
x
1
3
2
1 ...
]
)
(
[
1
1
1
)
(
...
)
(
)
(
2
1
2
2
2
2
2
2
1
2
∑
=
−
−
=
−
−
+
+
−
+
−
=
N
i
i
x
N
x
x
N
x
N
S
N
x
x
x
x
x
x
S
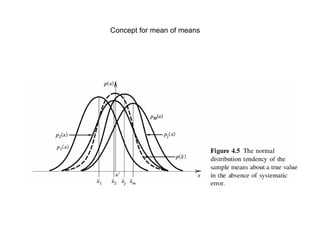
We want to estimate
x
u
x
x ±
=
'
ux is the uncertainty or confidence interval at some probability level P%
(P%)
x
x u
x
x
u
x −
≤
≤
− '

18. Mean of mean
Let’s imagine, we repeat the set of experiment for many times
Sn
…
S3
S2
S1
σ
…
x’
n
…
3
2
1
Sample
Population
1
x 2
x 3
x n
x

19. Concept for mean of means

20. Central limit theorem
If the sample is large, the distribution of the mean values is Gaussian and
that Gaussian distribution has a standard deviation
N
S
N
x
x ≈
=
σ
σ
The sample size N should be large
The distribution mean is Gaussian even if the underlying
population is not Gaussian

21. Statistical measurement theory
Measured values: X1, X2, X3, X4, X5, … XN
Sx
σ
X’
Sample measurement
Population
x
∑
=
+
+
+
+
=
=
N
i
N
i
N
x
x
x
x
N
x
x
1
3
2
1 ...
]
)
(
[
1
1
1
)
(
...
)
(
)
( 2
1
2
2
2
2
2
1
2
∑
=
−
−
=
−
−
+
+
−
+
−
=
N
i
i
N
x x
N
x
N
N
x
x
x
x
x
x
S
How good is the mean estimation?

22. Central limit theorem
The sample of the mean would show a dispersion about a central value. If N
is large, say larger 30, the distribution of the mean values is Gaussian and
that Gaussian distribution has a standard deviation
N
S
N
x
x
≈
=
σ
σ
The sample size N should be large, >30
The distribution of the means is Gaussian even if the underlying population is not Gaussian
A new distribution describing how good is the mean estimation
)
;
( x
S
x Distribution of
the population
)
;
(
N
S
x x Distribution of the
mean values

23. With this new distribution of the mean values, we can use the
sample data to estimate the true mean
N
S
N
x
x ≈
=
σ
σ
x
%
)
'
( P
u
x
x
u
x
P x
x =
+
<
≤
−
ux is the uncertainty or confidence interval at some probability level P%
x
x u
x
x
u
x −
≤
≤
− '

24. Procedure to find confidence interval of the mean
1. Check to see if N is larger than 30
2. Determine sample mean and standard deviation from data
3. Specify confidence interval, P%
4. Check table 4.3 to find the z value
5. Estimate the confidence interval
%
)
'
( P
u
x
x
u
x
P x
x =
+
<
≤
−
%
)
( P
z
z
P =
≤
≤
− β
N
S
z
x
x
N
S
z
x x
x
+
<
≤
− '
(P%)
N
S
z
x
x x
±
=
'

25. E.g. After 100 measurements, we find that the sample mean is 100
and the standard deviation is 20. Determine the best estimate of
the mean value at a 95% probability level

26. E.g.
30
100 >
=
N
1)
2
10
20
=
=
x
σ
100
=
x
2)
C.I. = 99% = 0.99
3)
C.I. = 0.99, i.e. 0.99/2 => 0.495 of area in Table 4.3
Z = 2.575
4)
5)
%)
99
(
15
.
5
10
'
15
.
105
'
85
.
94
100
20
575
.
2
'
100
20
575
.
2
100
'
±
=
<
≤
+
<
≤
−
+
<
≤
−
x
x
x
x
N
S
z
x
x
N
S
z
x x
x
After 100 measurements, we find that the sample mean is 100
and the standard deviation is 20. Determine the best estimate of
the mean value at a 95% probability level

27. If the sample size is small, say <30, a
better estimation on the confidence
interval can be obtained using the
Student’s t-distribution

28. Student’s t-distribution
ν=1
ν=2
ν=5
ν=10
ν=∞
The distribution depends on ν = N-1, degree of freedom

29. 0.1
0.2
t
-t
%
)
( P
t
t
P =
≤
≤
− β

30. Procedure to find confidence interval of the mean when sample size N is small
1. Determine ν = N-1, degree of freedom
2. Determine sample mean and standard deviation from data
3. Specify confidence, P%
4. Check table 4.4, tv,p
5. Calculate confidence interval
%
)
'
( P
u
x
x
u
x
P x
x =
+
<
≤
−
N
S
t
x
x
N
S
t
x
x
N
S
t
x
x
P
x
P
x
P
,
,
,
'
'
υ
υ
υ
±
=
+
<
≤
−
(P%)
%
)
( P
t
t
P =
≤
≤
− β

31. E.g. After 16 measurements, we find that the sample mean
is 100 and standard deviation 20. Determine a 99%
confidence interval for the measurement

32. E.g.
20
=
x
S
100
=
x
15
1=
−
= N
υ
C.I. = 99% = 0.99
t = 2.947
1)
2)
3)
4)
5)
%)
99
(
2
.
15
10
'
15
20
947
.
2
'
15
20
947
.
2
100
' ,
,
±
=
+
<
≤
−
+
<
≤
−
x
x
x
N
S
t
x
x
N
S
t
x x
p
x
p υ
υ
After 16 measurements, we find that the sample mean
is 100 and standard deviation 20. Determine a 99%
confidence interval for the measurement

33. Student’s t-test
Are two sets of data different?
Hypotheses testing
t value
2
2
1
1
,
,
S
x
S
x
2
2
2
1
2
1
2
1
N
s
N
s
x
x
t
+
−
=
1
1,S
x
2
2 ,S
x

34. Student’s t-test
Procedure
2
2
2
1
2
1
2
1
N
s
N
s
x
x
t
+
−
=
1. Find mean, S.D., and same size of data set 1 and set 2
2. Find degree of freedom
2
2
2
1
1
1
,
,
,
,
N
S
x
N
S
x
2
2
1 −
+
= N
N
υ
3. Calculate the t value
4. Specific P% confidence interval
5. Compare t value with table 4.4. If our calculated t value exceeds that
the tabulated value for tp, then we conclude that there is a significantly
different.

35. Example
Set A: 7.2, 7.6, 6.9, 8.2, 7.3, 7.8, 6.6, 6.9, 5.5, 7.4, 5.7, 6.2
Set B: 7.5, 8.7, 7.7, 7.5, 6.7, 11.2, 7.0, 10.7, 7.0, 8.6, 6.1, 6.3, 7.8, 8.7, 6.1
15
,
53
.
1
,
84
.
7
12
,
82
.
0
,
94
.
6
2
2
2
1
1
1
=
=
=
=
=
=
N
S
x
N
S
x
25
2
2
1 =
−
+
= N
N
υ
2)
1)
3) 954
.
1
15
53
.
1
12
82
.
0
84
.
7
94
.
6
2
2
2
2
2
1
2
1
2
1
−
=
+
−
=
+
−
=
N
s
N
s
x
x
t
4) For 95% confidence interval
08
.
2
22
,
2
/
05
.
0 ±
=
t
The calculated t falls within the region, we concluded that
there is not a significant difference in the two set of data

36. How do we determine P%, the probability level?
• If each error are estimated at the same probability level p%, the total
uncertainty will have the same probability level p%.
• A general, albeit somewhat arbitrary, rule is to use a 95% probability
level throughout all the uncertainty calculations. Engineers tend to
follow this 95% rule, and it is equivalent to assuming the probability
covered by two standard deviations. However, some prefer to use a
68% probability level (P% = 68%), which is equivalent to a spread of one
standard deviation. We (the book) use the 95% level in our calculation
but point out that other probability levels may be substituted, provided
they are applied consistently without any effect on the procedures.
• Normally, we decide the probability level of the uncertainty (confidence
interval)
• The probability level of the uncertainty level are given by the data sheet or
estimation from our calibration (distribution of the data)

37. A lab technician has just received a box of 2000 resistors. As a result of a production
error, the color-coded bands have not been painted on this lot. To determine the
nominal resistance and tolerance, the technician selects ten resistors and measures
their resistance with a digital multimeter. His results are as follow:
15.98
10
17.91
9
16.32
8
16.28
7
17.82
6
16.24
5
18.45
4
18.17
3
17.95
2
18.12
1
Resistance (kΩ)
Number
What is the nominal value of the resistors? What is the uncertainty in
that value? Can we estimate the tolerance?

38. Mean = 17.32 kΩ
Standard deviation = 0.982 kΩ
Consider the precision uncertainty, the t value is
262
.
2
9
%,
95
%, =
= t
tP υ
What is the nominal value of the resistors? What is the uncertainty in
that value? Consider both precision and bias uncertainty. Can we
estimate the tolerance?
Ω
±
=
±
=
±
= k
N
S
t
x
x p 70
.
0
32
.
17
10
982
.
0
262
.
2
32
.
17
' %,υ
The uncertainty of the nominal value is 0.70 kΩ or about 4%
The tolerance of the resistor is
Ω
±
=
×
±
=
±
= k
S
t
x
x p 22
.
2
32
.
17
982
.
0
262
.
2
32
.
17
' %,υ
The tolerance of the resistor is 2.22kΩ or 13% (95%)