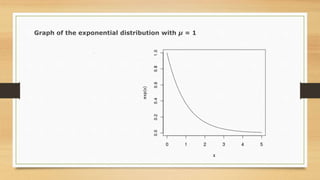
The exponential probability distribution is useful for describing the time it takes to complete random tasks. It can model the time between events like vehicle arrivals at a toll booth, time to complete a survey, or distance between defects on a highway. The distribution is defined by a probability density function that uses the mean time or rate of the process. It can calculate the probability that an event will occur within a certain time threshold, like the chance a car will arrive at a gas pump within 2 minutes. The mean and standard deviation of the exponential distribution are equal, and it is an extremely skewed distribution without a defined mode.

1. M.BILAL
TARIQ
SUFIAN
IQBAL
M.NAVEED

2. Exponential Probability
Distribution

3. The exponential probability distribution is useful in describing the
time it takes to complete a task.
The exponential random variables can be used to describe:
Time between vehicle arrivals at a toll booth
Time required to complete a questionnaire
Distance between major defects in a highway
The time between goals scored in a World Cup
soccer match

4. f x e x
( ) /
 1


for x > 0,  > 0
Density Function
where:  = mean
e = 2.71828

5. Cumulative Probabilities
P x x e x
( ) /
   
0 1 o 
where:
x0 = some specific value of x

6. Example: Al’s Full-Service Pump
The time between arrivals of cars at Al’s full-service gas pump follows
an exponential probability distribution with a mean time between
arrivals 3 minutes. Al would like to know the probability that the time
between two successive arrivals will be 2 minutes or less.
P(x < 2) = 1 - 2.71828-2/3 = 1 - .5134 = .4866
Solution:

7. Example:
If jobs arrive every 15 seconds on average, λ = 4 per minute,
what is the probability of waiting less than or equal to 30
seconds, i.e .5 min? P(T ≤ .5).

8. Characteristics :
The mean and standard deviation of exponential distribution are equal.
The distribution is extremely skewed and there does not exist any mode.

9. .
Graph of the exponential distribution with μ = 1

11. QUESTION