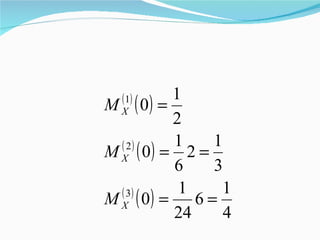The document defines the moment generating function (MGF) of a random variable X as the expectation of e^tx, provided the expectation exists in some neighborhood of 0. The MGF fully characterizes the distribution of X and can be used to find moments. For the uniform distribution on [0,1], the MGF is (e^t - 1)/t. For the normal distribution with mean μ and variance σ^2, the MGF is e^(tμ + 1/2t^2σ^2). The MGF of independent random variables X and Y is the product of their individual MGFs.

1. EDWIN OKOAMPA BOADU

2. DEFINITION Definition 2.3.3. Let X be a random variable with cdf F X . The moment generating function (mgf) of X (or F X ), denoted M X (t) , is provided that the expectation exists for t in some neighborhood of 0. That is, there is an h >0 such that, for all t in – h < t < h , E [ e tX ] exists.

3. If the expectation does not exist in a neighborhood of 0, we say that the moment generating function does not exist. More explicitly, the moment generating function can be defined as:

4. Theorem 2.3.2: If X has mgf M X ( t ), then where we define

5. First note that e tx can be approximated around zero using a Taylor series expansion:

6. Note for any moment n: Thus, as t  0

7. Leibnitz’s Rule: If f ( x ,θ), a (θ), and b (θ) are differentiable with respect to θ, then

8. Berger and Casella proof: Assume that we can differentiate under the integral using Leibnitz’s rule, we have

9. Letting t ->0, this integral simply becomes This proof can be extended for any moment of the distribution function.

10. Moment Generating Functions for Specific Distributions Application to the Uniform Distribution:

11. Following the expansion developed earlier, we have:

12. Letting b =1 and a =0, the last expression becomes: The first three moments of the uniform distribution are then:

14. Application to the Univariate Normal Distribution

15. Focusing on the term in the exponent, we have

16. The next state is to complete the square in the numerator.

17. The complete expression then becomes:

18. The moment generating function then becomes:

19. Taking the first derivative with respect to t , we get: Letting t ->0, this becomes:

20. The second derivative of the moment generating function with respect to t yields: Again, letting t ->0 yields

21. Let X and Y be independent random variables with moment generating functions M X ( t ) and M Y ( t ). Consider their sum Z = X + Y and its moment generating function:

22. We conclude that the moment generating function for two independent random variables is equal to the product of the moment generating functions of each variable.

23. Skipping ahead slightly, the multivariate normal distribution function can be written as: where Σ is the variance matrix and μ is a vector of means.

24. In order to derive the moment generating function, we now need a vector t . The moment generating function can then be defined as:

25. Normal variables are independent if the variance matrix is a diagonal matrix. Note that if the variance matrix is diagonal, the moment generating function for the normal can be written as: