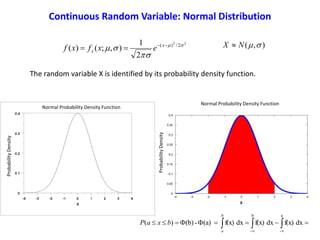
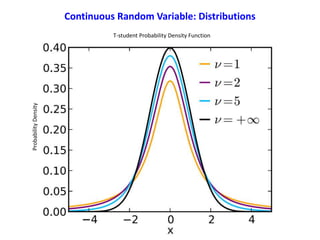
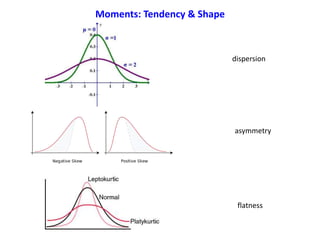
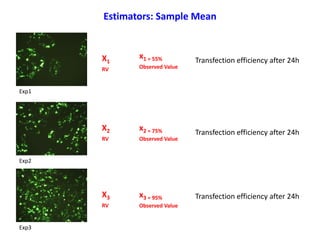
The document provides an overview of key statistical concepts including: - Random variables and their probability distributions and functions - Common estimators like the sample mean and variance - The distributions of common estimators and how they relate to the underlying population parameters - Confidence intervals and how they are used to quantify the uncertainty in estimates based on sample data - 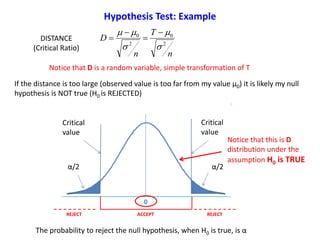Hypothesis testing framework including defining the null and alternative hypotheses, calculating a test statistic, and determining whether to reject or fail to reject the null based on probability thresholds

1. Statistics Applied to
Biomedical Sciences
Luca Massarelli
@ UCLA - Anesthesiology Department
Division of Molecular Medicine
April 10, 2014

2. Outline
 Random variables: definition & properties
 Estimators: sample mean & sample variance
 Distributions of estimators
 Confidence interval
 Hypothesis test
 Application to biomedical experiments: z-Test, t-Test & ANOVA

3. Classification:
- Discrete
- Continuous
Random Variable: Definition
- A random variable is a real-valued function defined on a set of possible outcomes,
the sample space Ω.
-Probability distribution is a function which maps each value of the random variable
to a probability
-Cumulative Distribution is a function that, given the probability distribution,
determines the probability at a value less than or equal to x

4. We will extract 2 persons from West LA population and we will consider the number of
persons affected by a certain allergy in spring.
Probability of people with allergy = 20%
random variable
Probability distribution function
Cumulative distribution function
(D1,D2) ---- > 0
(D1,D2) ---- > 1
(D1,D2) ---- > 1
(D1,D2) ---- > 2
X f(x) Φ(x)
0 0.64 0.64
1 0.32 0.96
2 0.04 1.00
Probability distribution function: f(x) = P(X=x)
 

xxi
x)P(X(x) xi
fCumulative distribution function
X: Ω ---- > R
Ω = {(D1,D2), (D1,D2), (D1,D2), (D1,D2) }
Random Variable: Discrete

5. Probability density function:
Cumulative distribution function
f(x) is related to the following eq.


x
-
dxf(x)x)P(X(x)
Random Variable: Continuous

6. Normal Probability Density Function
ProbabilityDensity
x
22
2/)(
2
1
),;()( 

 
 x
x exfxf
The random variable X is identified by its probability density function.
),( NX 
Normal Probability Density Function
ProbabilityDensity
  
a
-
b
-
b
dxf(x)dxf(x)dxf(x)(a)-(b))(
a
bxaP
Continuous Random Variable: Normal Distribution

7. T-student Probability Density FunctionProbabilityDensity
Continuous Random Variable: Distributions

8. Moment is a quantitative measure of the shape of a set of points.



 dxxfcxcxE nn
n
)()()(Moment
The nth moment of a random variable about a value c



 dxxxfxE )()(Mean: Central tendency.
 


 dxxfxExVAR x )()()( )(
2
22
 Variance Dispersion around the mean.
Information about the shape of a distribution
 


 dxxfxE x )()( )(
3
3
Skewness Asymmetry around the mean.
 


 dxxfxE x )()( )(
4
4
Kurtosis Measure of flatness
Moments: Tendency & Shape

9. dispersion
asymmetry
flatness
Moments: Tendency & Shape

10. It is a function of random variables whose values are used to estimate a certain
parameter.
T = t(Xi) where Xi has a given distribution with unknown θ (parameter), which is the
target of our statistic.
Xi is the i-th observable random variable
X1, X2, X3, … Xn is a sample of random variables extracted from a population;
Population has a certain probability density function f(x)
Estimators: Definition
The Transformation of Random variable is still a random variable: Addition,
Subtraction, Multiplication and Divisions results in another random variable

11. Estimator has some desirable properties:
UNBIASED
The estimator is an unbiased estimator of θ if and only if
E(T) = θ --- > (E(T) – θ) = 0
In other words the distance between the average of the collection of estimates and
the single parameter being estimated is null.
Bias is a property of the estimator, not of the estimate.
1}|{|lim 

TP
n
EFFICIENCY
The estimator has minimal mean squared error (MSE) or variance of the estimator
MSE(T) = E[T- θ]2
If I have an estimator with smaller dispersion, I will have more probability to find an
estimation which is closer to the TRUE Parameter.
CONSISTENCY
Increasing the sample size increases the probability of the estimator being close to
the population parameter.
Estimators: Properties

12. SAMPLE MEAN estimator for μ
Sample mean is an unbiased estimator of μ INDIPENDENTLY of the distribution of
the random variable X.
Sample mean is an efficient estimator of μ in case of Normal, Poisson, Exponential,
Bernoulli distribution.


n
i
iX
n
T
1
1
Estimators: Sample Mean

13. Exp1
X1
RV
x1 = 55%
Observed Value
Exp2
X2
RV
x2 = 75%
Observed Value
Exp3
X3
RV
x3 = 95%
Observed Value
Transfection efficiency after 24h
Transfection efficiency after 24h
Transfection efficiency after 24h
Estimators: Sample Mean

14.  
)()
1
()(
1
i
n
i
i XEX
n
ETE
n
XnVAR
n
X
n
VARTVAR i
n
i
i
2
2
1
)(
1
)
1
()(

 
It is unbiased and (under certain conditions) efficient for μ!
Using the sample mean I can take some conclusions:
• the E(T) on average tends to μ (Unbiased Property)
• my estimation is reasonable in a certain level of uncertainty (Std Error)
• by increasing n, I can decrease the error of my estimation
n
StdError




n
i
iX
n
T
1
1
Why Sample Mean?
According to the observed values the estimation of μ = 75%
(x1, x2, x3) is just one vector of the potential one. I could have had any other value.
Are we close or far from the real value of μ?
Estimators: Sample Mean

15. SAMPLE VARIANCE estimator for δ22
1
)(
1
TX
n
S
n
i
i  
n
n
SE
1
)( 2 
 
2
1
'
)(
1
1
1
TX
n
S
n
n
S
n
i
i 



 
2
)'( SE
According to the observed values the estimation of σ2 = 4%
(variance has been corrected by n/(n-1))
Assuming that Xi are INDIPENDENT it can be demonstrated that:
--- > distorted estimator
(sample variance as defined above would be unbiased only if μ of population is known)
SAMPLE VARIANCE
Estimators: Sample Variance
This estimator depends on n random variables (Xi) and the random variable sample
mean.

16. SAMPLE MEAN 

n
i
iX
n
T
1
1
Assuming that ),( 2
NX 
),(
2
n
NT


N(μ, δ2/n)
n

 2
n

 2
then
Distribution of Estimators

17. SAMPLE VARIANCE 2
1
'
)(
1
1
TX
n
S
n
i
i 

 
Assuming that ),( 2
NX 
1
2
2
'
1


 n
n
S 
then
Distribution of Estimators

18. 

n
i
iX
n
T
1
1
),( 2
NX 
2
1
'
)(
1
1
TX
n
S
n
i
i 

 
1
2
2
'
1


 n
n
S 

),(
2
n
NT


1
1
22'
1
1








 n
n
Tstudent
n
n
T
n
S
T
D


with μ and σ2 are unknownAssuming that
Normal Distr.
χ2 Distr.
Distribution of Estimators: Distance

19. A confidence interval (CI) is a type of interval which estimates a certain parameter of
a population.
Confidence interval (which is calculated from the observations), is that interval that
frequently includes the parameter of interest if the experiment is repeated.
The probability that the observed interval contains the parameter is determined by
the confidence level or confidence coefficient.
CI95% for μ means that I want to determine an interval being sure that 95% of the
time the TRUE MEAN of the population lies somewhere within my interval.
Confidence Interval: Definition

20. ),( 2
NX 
Assuming my population
has a normal distribution
Set of n experiments
Set of n experiments
Set of n experiments
Set of n experiments
Set of n experiments
Set of n experiments
Set of n experiments
...
We will never determine
the TRUE VALUE of μ
Confidence Interval: Definition

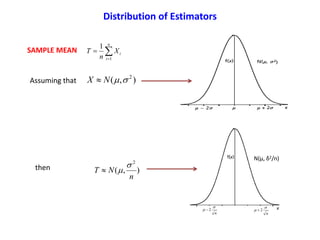
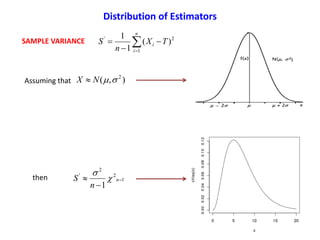
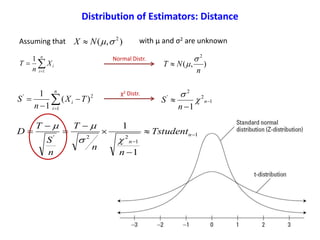
21. )(TE
n
TVAR
2
)(


n
StdError



n
i
iX
n
T
1
1
If ),( 2
NX  ),(
2
n
NT


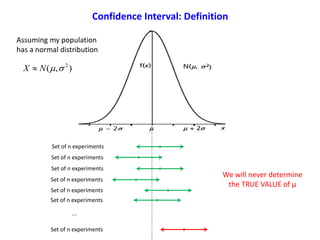
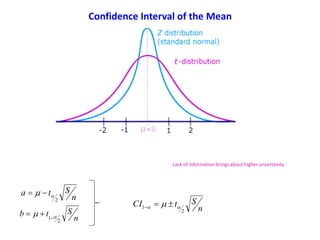
Define an interval around our estimate of μ with confidence coeff. = 95%
 1][Pr bTaob
With the transformation to a Standard Normal Distribution













1][Pr
222
n
b
n
T
n
a
ob









1][Pr
22
n
b
Z
n
a
ob  

1][Pr
2
12
ZZZob
Confidence Interval of the Mean
Normal Probability Density Function
ProbabilityDensity
x

22. Here we are assuming σ2 is known. What if the variance is unknown?
 

1][Pr
2
12
ZZZob
n
Zb
2
2
1
 

 1][Pr bTaob
Zα/2 0 Z1-α/2 a μ b
n
Za
2
2
 
n
ZCI
2
2
1
  
Confidence Interval of the Mean

23. Zα/2 Z1- α /2
tα/2 t1- α /2
n
Stb
2
1  

n
Sta
2
 
n
StCI
2
1   
Lack of information brings about higher uncertainty
Confidence Interval of the Mean

24. • Coefficient 1-α. Increasing the probability that the interpretation of an
experiment is correct requires to make the interval larger.
• Number of Experiments. SE of Estimator can be reduced increasing n.
• Available information about the population.
The lack of information about the population brings about a bigger uncertainty
which is reflected in a larger interval.
These considerations will be similarly apply to the Hypothesis Test.
Confidence Interval: Considerations

25. The test is based on the following MODEL:
a) Assume that the treatment has NO effect on the underlying population (H0)
b) Set a variable which measures the DISTANCE of the means
c) Distance is associated with a probability under the assumption that the treatment
has no effect (H0 is TRUE)
Hypothesis Test: Definition
It is a statistical tool used to determine what results would lead to accept or reject a
certain hypothesis for a pre-specified level of significance (α).
H0 - Null Hypothesis: μ=μ0
H1 - Alternative Hypothesis μ ≠ μ0
The hypothesis test here assumes the following statements:
a) we have 1 population where we know the distribution and sometimes its
parameters (i.e. mean and variance)
b) from the underlying population we have extracted one or more groups of subjects
(sample or set of the experiment)
c) we have applied a certain treatment to our samples

26. n
T
n
D
2
0
2
0



 


DISTANCE
(Critical Ratio)
If the distance is too large (observed value is too far from my value μ0) it is likely my null
hypothesis is NOT true (H0 is REJECTED)
The probability to reject the null hypothesis, when H0 is true, is α
Notice that D is a random variable, simple transformation of T
ACCEPT REJECTREJECT
Critical
value
Critical
value
α/2α/2
0
Notice that this is D
distribution under the
assumption H0 is TRUE
0
Hypothesis Test: Example

27. REJECT H0 if |D|≥dα
ACCEPT H0 if |D|≤dα
p-value
Given the DISTANCE, what is the probability that the sample differs from the underlying
population, when the NULL HYPOTHESIS is TRUE?
p-value is the probability of observing a distance that is as extreme or more extreme
than currently observed, assuming that the NULL HYPOTHESIS is TRUE
It is a measure of making a mistake. It is the risk that you reject NULL HYPOTESIS given
the fact that it is true.
ACCEPT REJECTREJECT
Critical
value
Critical
value
α/2α/2
0-dα dα
n
T
n
D
2
0
2
0



 



d
.
p-value
p-value > α
Accept H0
d
.
p-value
p-value < α
Reject H0
Hypothesis Test: p-value

28. Scientific Assumptions:
- the true mean of underling population is known
- the true SD of underling population is known
Statistical Assumptions:
- the underlying distribution is NORMAL
- the sample is chosen randomly from the underlying population
Hypothesis definition
H0 - Null Hypothesis: μ=μ0 or μ-μ0 = 0
H1 - Alternative Hypothesis μ ≠ μ0
Hypothesis Test: one Sample z-Test

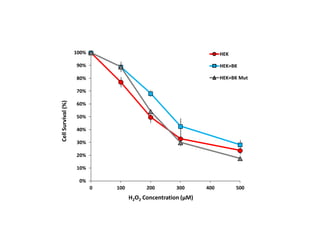
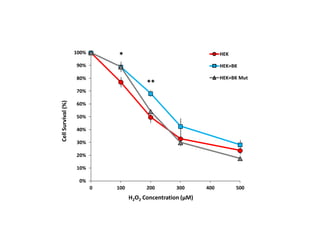
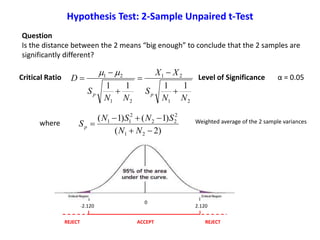
29. Question
Based on Mean comparison, on average, did TRTM treatment really change the level
of survival of the general population?
HEK cells
[H2O2] = 200 μM
We assume that the survival probability of HEK cells follows the normal distribution
with the following known parameters.
μ0 = 62%
σ = 15.5%
Assume that one sample of HEK population is extracted and submitted to a certain
treatment (TRTM)
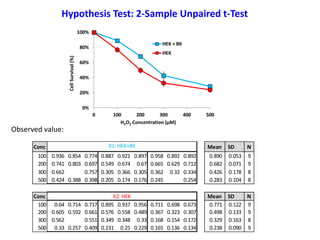
Observed value:
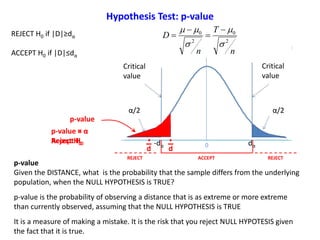
Hypothesis Test: one Sample z-Test
Exp. Observed Values
1 0.605
2 0.592
3 0.661
4 0.367
5 0.323
6 0.307
Sample Mean 0.476
SD 0.160
SE 0.065

30. n
T
n
D
2
0
2
0



 


Critical Ratio Level of Significance α = 0.05
ACCEPT REJECTREJECT
The distance between sample and known mean is 2.278 units.
We can conclude that the treatment significantly decreased the percentage of survival. The
chance of wrongly reject the null hypothesis is much less than 5%.
Hypothesis Test: one Sample z-Test
Description Observed Values
Mean (Population) 0.6200
Mean (observed) 0.4758
SD known 0.1550
Observations 6
Hypothesized Mean
Difference
-
D -2.2783
p value - 1 tail 0.0116
p value - 2 tails 0.0233

31. Scientific Assumptions:
- the true mean of underling population is known
- the true SD of underling population is NOT known
Hypothesis definition
H0 - Null Hypothesis: μ=μ0 or μ-μ0 = 0
H1 - Alternative Hypothesis μ ≠ μ0
Hypothesis Test: one Sample t-Test
Statistical Assumptions:
- the underlying distribution is NORMAL
- the sample is chosen randomly from the underlying population

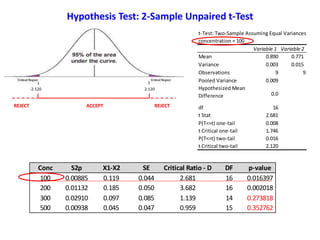
32. Question
Based on Mean comparison, on average, did TRTM treatment really change the level
of survival of the general population?
Let’s assume that the survival probability of HEK cells follow the normal distribution
with the following known parameters.
μ0 = 62%
σ = unknown
Assume that one sample of HEK population is extracted and submitted to treatment
TRTM
Observed value:
HEK cells
[H2O2] = 200 μM
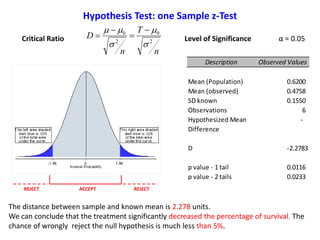
Hypothesis Test: one Sample t-Test
Exp. Observed Values
1 0.605
2 0.592
3 0.661
4 0.367
5 0.323
6 0.307
Sample Mean 0.476
SD 0.160
SE 0.065

33. n
S
T
n
S
D
2
0
2
0  


Critical Ratio Level of Significance α = 0.05
The distance between sample and known mean is 2.206 units.
We can conclude that the treatment did NOT significantly decreased the percentage of cell
survival. The chance of wrongly reject the null hypothesis is grater than 5%.
ACCEPT REJECTREJECT
2.447-2.447
Hypothesis Test: one Sample t-Test
0
Description Observed Values
Mean (Population) 0.6200
Mean (observed) 0.4758
Variance estimated 0.1601
Observations 6
Hypothesized Mean
Difference
-
Degree of Freedom (n-1) 5
D -2.2060
p value - 1 tail 0.0392
p value - 2 tails 0.0784

34. Scientific Assumptions:
- we estimate the MEAN DIFFERENCE between pairs for an underlying population
- we estimate the SD of the distribution of differences
Hypothesis definition
H0 - Null Hypothesis: μDiff = 0
H1 - Alternative Hypothesis μDiff > 0 (one tail)
Hypothesis Test: 2-Sample Paired t-Test
Statistical Assumptions:
- the underlying distribution is NORMAL
- the sample is chosen randomly from the underlying population

35. Hypothesis Test: 2-Sample Paired t-Test
data
Membrane Potential (mV)
Membrane Potential (mV) Membrane Potential (mV)
NormalizedConductance
NormalizedConductance
NormalizedConductance
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
-100 -50 0 50 100
G(V) (before)
G(V) CARDAMONIN (after)
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
-100 -50 0 50 100
G(V) (before)
G(V) CARDAMONIN (after)
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
-100 -50 0 50 100
G(V) (before)
G(V) CARDAMONIN (after)

36. Question
On average is the observed difference significantly more than 0? Is the distance big
enough to conclude that the treatment/drug had effect?
Hypothesis Test: 2-Sample Paired t-Test
n
S
T
D
Diff
2
0

Critical Ratio
Vm
(mV)
Diff.
Exp1
Diff.
Exp2
Diff.
Exp3
Mean Diff.
(Tdiff)
SD
Diff.
D - Critcal
Ratio
-100 0.005 -0.005 -0.002 -0.001 0.005 -0.211
-90 0.003 -0.007 0.010 0.002 0.008 0.445
-80 0.003 -0.002 0.010 0.004 0.006 1.072
-70 -0.002 -0.003 0.005 0.000 0.005 -0.010
-60 0.000 0.000 -0.004 -0.001 0.003 -0.970
-50 -0.001 -0.004 -0.009 -0.005 0.004 -1.904
-40 0.009 -0.018 -0.017 -0.009 0.016 -0.957
-30 0.002 -0.042 0.014 -0.009 0.029 -0.530
-20 0.003 -0.061 0.073 0.005 0.067 0.126
-10 0.018 -0.025 0.076 0.023 0.051 0.790
0 0.042 0.022 0.065 0.043 0.022 3.427
10 0.067 0.069 0.053 0.063 0.009 12.436
20 0.096 0.104 0.044 0.082 0.033 4.323
30 0.117 0.116 0.047 0.093 0.040 4.046
40 0.123 0.119 0.040 0.094 0.047 3.486
50 0.115 0.099 0.041 0.085 0.039 3.785
60 0.104 0.076 0.017 0.066 0.045 2.546
70 0.087 0.052 0.027 0.055 0.030 3.165
80 0.064 0.039 0.013 0.038 0.025 2.611
90 0.042 0.026 0.005 0.025 0.019 2.259
100 0.038 0.021 0.020 0.026 0.010 4.442

37. n
S
T
D
Diff
2
0
Critical Ratio
Level of Significance α = 0.05
Case -10 mV: After cardamonin treatment, the increase of mean conductance is indicated by a
distance of 0.79 units away from 0. Thus, the NULL Hypothesis is ACCEPTED.
Hypothesis Test: 2-Sample Paired t-Test
Hypothesis definition
H0 - Null Hypothesis: μDiff = 0
H1 - Alternative Hypothesis μDiff > 0
Case 30 mV : After cardamonin treatment, the increase of mean conductance is indicated by a
distance of 4.05 units away from zero. Thus, the NULL Hypothesis is REJECTED.
With α set at 5%, then the critical value for this study is 2.92.
ACCEPT REJECT
2.920
0 2.92
Vm
(mV)
Diff.
Exp1
Diff.
Exp2
Diff.
Exp3
Mean Diff.
(Tdiff)
SD
Diff.
D - Critcal
Ratio
p-value
-20 0.003 -0.061 0.073 0.005 0.067 0.126 0.4556
-10 0.018 -0.025 0.076 0.023 0.051 0.790 0.2562
0 0.042 0.022 0.065 0.043 0.022 3.427 0.0378
10 0.067 0.069 0.053 0.063 0.009 12.436 0.0032
20 0.096 0.104 0.044 0.082 0.033 4.323 0.0248
30 0.117 0.116 0.047 0.093 0.040 4.046 0.0280
40 0.123 0.119 0.040 0.094 0.047 3.486 0.0367

38. Scientific Assumptions:
- we compare only TWO groups
- both the 2 samples have comparable experimental conditions
Statistical Assumptions:
- the underlying distribution is NORMAL
- both the 2 samples have equal variance
Hypothesis definition
H0 - Null Hypothesis: μ1 =μ2 or μ1 - μ2 = 0
H1 - Alternative Hypothesis μ ≠ μ0
Hypothesis Test: 2-Sample Unpaired t-Test

39. Observed value:
Hypothesis Test: 2-Sample Unpaired t-Test
H2O2 Concentration (μM)
CellSurvival(%)
0%
20%
40%
60%
80%
100%
0 100 200 300 400 500
HEK + BK
HEK
Conc Mean SD N
100 0.936 0.854 0.774 0.887 0.921 0.897 0.958 0.892 0.892 0.890 0.053 9
200 0.741 0.803 0.697 0.549 0.674 0.67 0.665 0.629 0.712 0.682 0.071 9
300 0.662 0.757 0.305 0.366 0.305 0.362 0.32 0.334 0.426 0.178 8
500 0.424 0.388 0.398 0.205 0.174 0.176 0.245 0.254 0.283 0.104 8
Conc Mean SD N
100 0.64 0.714 0.717 0.895 0.937 0.956 0.711 0.698 0.673 0.771 0.122 9
200 0.605 0.592 0.661 0.576 0.558 0.489 0.367 0.323 0.307 0.498 0.133 9
300 0.562 0.551 0.349 0.348 0.33 0.168 0.154 0.172 0.329 0.163 8
500 0.33 0.257 0.409 0.231 0.25 0.229 0.165 0.136 0.134 0.238 0.090 9
X1: HEK+BK
X2: HEK

40. Question
Is the distance between the 2 means “big enough” to conclude that the 2 samples are
significantly different?
Critical Ratio Level of Significance α = 0.05
21
21
21
21
1111
NN
S
XX
NN
S
D
pp 






where
)2(
)1()1(
21
2
22
2
11



NN
SNSN
Sp
Weighted average of the 2 sample variances
ACCEPT REJECTREJECT
-2.120 2.120
Hypothesis Test: 2-Sample Unpaired t-Test
0

41. ACCEPT REJECTREJECT
-2.120 2.120
t-Test: Two-Sample Assuming Equal Variances
concentration = 100
Variable 1 Variable 2
Mean 0.890 0.771
Variance 0.003 0.015
Observations 9 9
Pooled Variance 0.009
Hypothesized Mean
Difference 0.0
df 16
t Stat 2.681
P(T<=t) one-tail 0.008
t Critical one-tail 1.746
P(T<=t) two-tail 0.016
t Critical two-tail 2.120
Conc S2p X1-X2 SE Critical Ratio - D DF p-value
100 0.00885 0.119 0.044 2.681 16 0.016397
200 0.01132 0.185 0.050 3.682 16 0.002018
300 0.02910 0.097 0.085 1.139 14 0.273818
500 0.00938 0.045 0.047 0.959 15 0.352762
Hypothesis Test: 2-Sample Unpaired t-Test

42. When more than 2 means within one analysis need to be compared simultaneously,
pairwise t-Test would be less appropriate.
The composite chance of making mistake increases with the number of pairwise tests.
# Parwise Test Variables Confidence Int. Error Type I
1 2 95.0% 5.0%
2 3 90.3% 9.8%
3 4 85.7% 14.3%
4 5 81.5% 18.5%
5 6 77.4% 22.6%
Hypothesis Test: ANOVA

43. Scientific Assumptions:
-You are comparing two or more groups
-The true mean of the underlying population is UNKNOWN
-The true SD of the underlying population is UNKNOWN
Hypothesis definition
H0 - Null Hypothesis: μ1 = μ2 = μ3 = μ4 … = μk
H1 - Alternative Hypothesis μi ≠ μj at least for 1 pairwise
Hypothesis Test: ANOVA
Statistical Assumptions:
- the underlying distribution is NORMAL
- samples have equal variance

44. How big this variance (VB) must be to indicate that the samples probably did not
come from the same underlying population?
Hypothesis Test: ANOVA
If the NULL hypothesis is true:
All the sample means should be valid estimators of μ: the sample means should
be fairly close to each other.
VB = variance between the sample means
VW=variance of each sample
VarianceDecomposition.xlsx

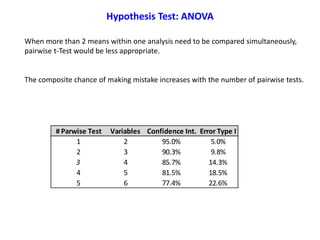
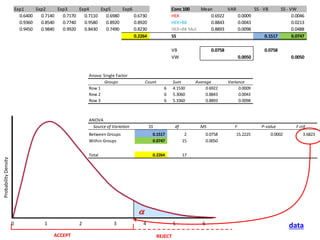
45. The variance of the underlying population σ2 could be estimated by 2 different methods:
a) The variance of the sample means
b) The average of the sample variances
1
])(...)()([ 22
22
2
11



K
XxnXxnXxn
VB kk
Assuming that each group has the same n, VB can be simplified as follows:
1
)(
1
2




K
Xxn
VB
K
k
k
   


K
k
n
i
kik
K
k
k
n
Xx
K
S
K
VW
1 1
2
1
2
1
)(11
Variance Between:
We know that the variance of the sample means is equal to the SE or δ2 /n
Variance Within:
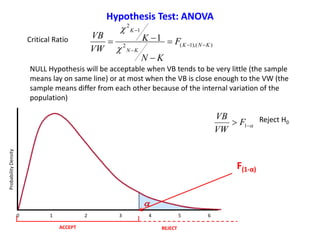
Hypothesis Test: ANOVA

46. Under these assumptions, we expect that:
Critical Ratio
VW
VB
Hypothesis Test: ANOVA
OR
at least the VB tend to be as small as possible.
VB and VW should converge to the same value

47. Critical Ratio
)(),1(2
1
2
1
KNK
KN
K
F
KN
K
VW
VB








NULL Hypothesis will be acceptable when VB tends to be very little (the sample
means lay on same line) or at most when the VB is close enough to the VW (the
sample means differ from each other because of the internal variation of the
population)
Reject H0
Hypothesis Test: ANOVA
0 ……………………1 …….………………2 ……….……………3 …………………4………………… 5………………… 6
ACCEPT REJECT
 1F
VW
VB
ProbabilityDensity
F(1-α)

48. H2O2 Concentration (μM)
CellSurvival(%)
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0 100 200 300 400 500
HEK
HEK+BK
HEK+BK Mut

49. 0 ……………………1 …….………………2 ……….……………3 …………………4………………… 5………………… 6
ACCEPT REJECT
ProbabilityDensity
Anova: Single Factor
Groups Count Sum Average Variance
Row 1 6 4.1530 0.6922 0.0009
Row 2 6 5.3060 0.8843 0.0043
Row 3 6 5.3360 0.8893 0.0098
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 0.1517 2 0.0758 15.2225 0.0002 3.6823
Within Groups 0.0747 15 0.0050
Total 0.2264 17
data
Exp1 Exp2 Exp3 Exp4 Exp5 Exp6 Conc 100 Mean VAR SS - VB SS - VW
0.6400 0.7140 0.7170 0.7110 0.6980 0.6730 HEK 0.6922 0.0009 0.0046
0.9360 0.8540 0.7740 0.9580 0.8920 0.8920 HEK+BK 0.8843 0.0043 0.0213
0.9450 0.9840 0.9920 0.8430 0.7490 0.8230 HEK+BK Mut 0.8893 0.0098 0.0488
0.2264 SS 0.1517 0.0747
VB 0.0758 0.0758
VW 0.0050 0.0050

50. H2O2 Concentration (μM)
CellSurvival(%)
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0 100 200 300 400 500
HEK
HEK+BK
HEK+BK Mut
*
**