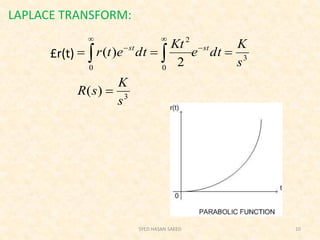
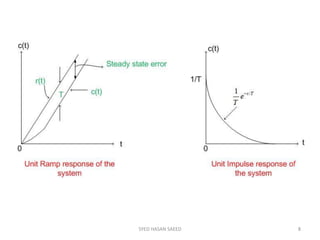
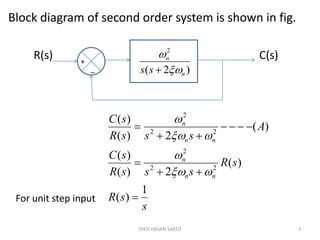
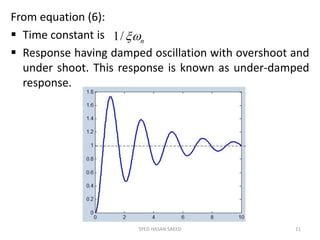
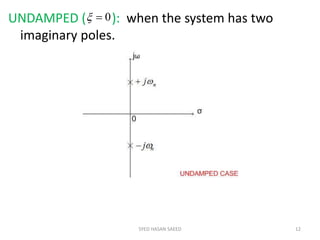
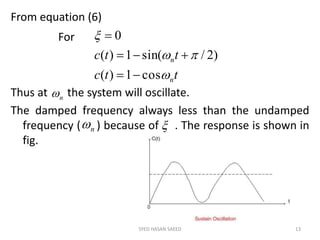
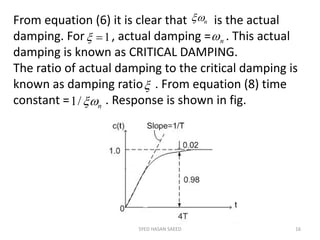
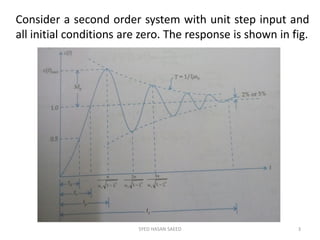
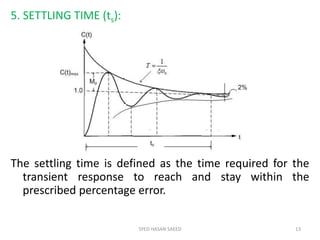
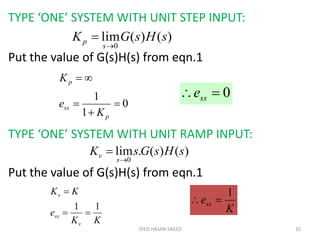
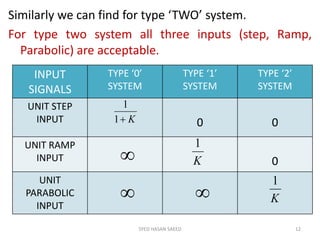
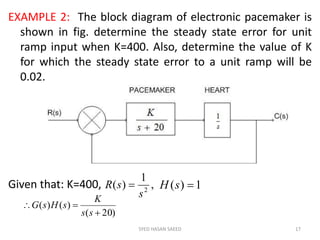
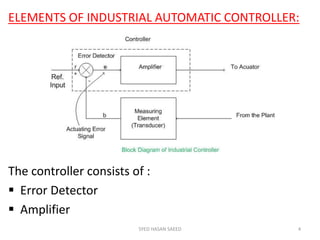
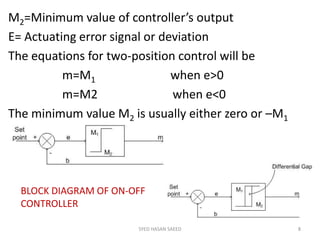
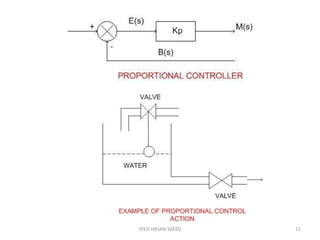
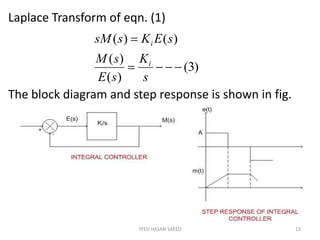
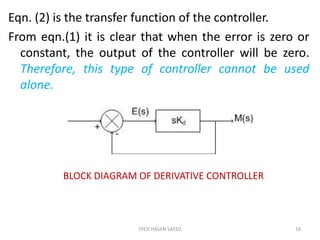
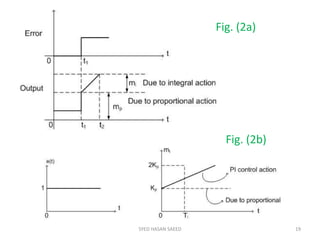
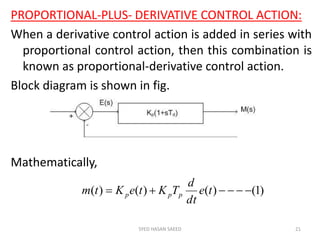
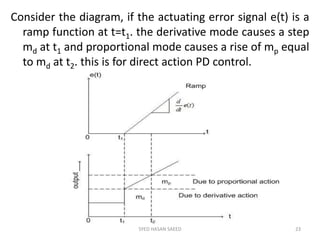
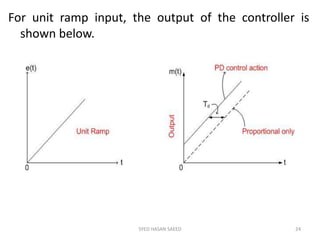
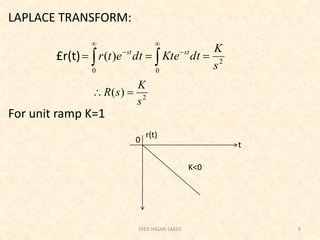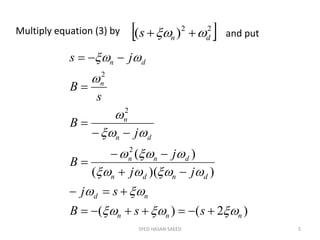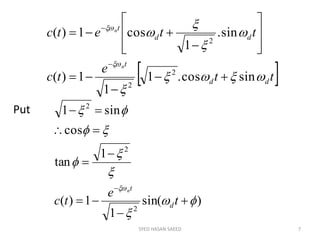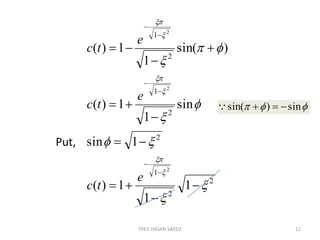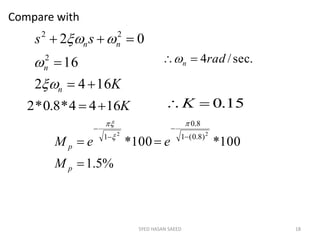The document provides an extensive overview of time domain analysis in control systems, covering key concepts such as transient response, steady state response, and steady state error. It explains various input signals like step, ramp, and parabolic functions, along with their mathematical representations and impacts on system response. Additionally, it discusses the responses of first and second-order systems to different inputs and characterizes system behaviors based on parameters such as damping factor.