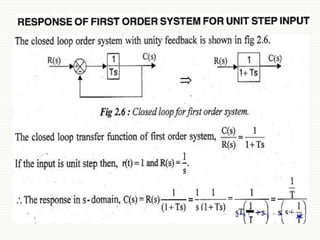
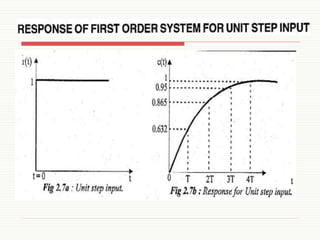
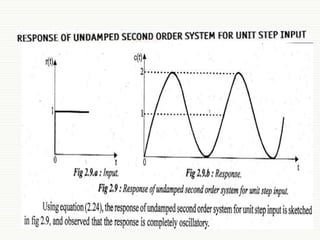
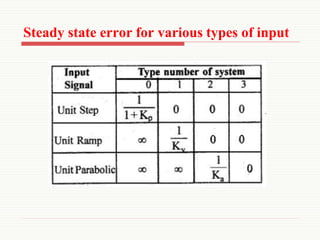
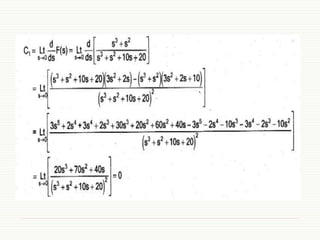
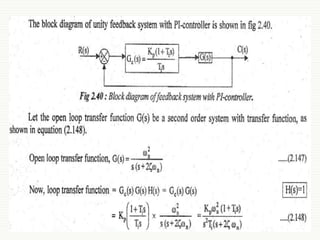
This document summarizes key concepts about first and second order control systems. It discusses: - The characteristics of a first order system, which has one pole and is defined by its DC gain (K) and time constant (T). - Examples of first order systems and how to determine their DC gain and time constant. - That a second order system can have different responses depending on its parameters, such as damped or undamped oscillations. - How to determine the undamped natural frequency and damping ratio of a second order system by comparing its transfer function to the general second order transfer function. The document then provides example problems for determining properties of first and second order systems. It concludes by

1. First & Second Order of the Control Systems
Presented by
Mr. C.S.Satheesh, M.E.,
Assistant Professor, Department of EEE,
Muthayammal Engineering College (Autonomous),
Namakkal (Dt), Rasipuram – 637408
MUTHAYAMMAL ENGINEERING COLLEGE
(An Autonomous Institution)
(Approved by AICTE, New Delhi, Accredited by NAAC, NBA & Affiliated to Anna University),
Rasipuram - 637 408, Namakkal Dist., Tamil Nadu, India.

2. Order system

3. Introduction - First order system
 The first order system has only one pole.
 Where
K is the D.C gain and
T is the time constant of the system.
 Time constant is a measure of how quickly a 1st order
system responds to a unit step input.
 D.C Gain of the system is ratio between the input signal
and the steady state value of output.
1


Ts
K
s
R
s
C
)
(
)
(

4. First order system
 Examples:
 The first order system given below.
1
3
10


s
s
G )
(
5
3


s
s
G )
(
1
5
1
5
3


s
/
/
• D.C gain is 10 and time constant is 3 seconds.
• For the following system
• D.C Gain of the system is 3/5 and time constant is 1/5 seconds.

10. Second Order System
 We have already discussed the transient response of 1st order
systems.
 Compared to the simplicity of a first-order system, a second-order
system exhibits a wide range of responses that must be analyzed
and described.
 Whereas, changes in the parameters of a second-order system can
change the form of the response.
 A second-order system can display characteristics much like a
first-order system or, depending on component values, display
damped or pure oscillations for its transient response.
10

15. t
t
c n

cos
1
)
( 


17. Problem 1
4
2
4
)
(
)
(
2



s
s
s
R
s
C
 Determine the un-damped natural frequency
and damping ratio of the following second
order system.
4
2

n

2
2
2
2 n
n
n
s
s
s
R
s
C






)
(
)
(
• Compare the numerator and denominator of the given transfer
function with the general 2nd order transfer function.
2

 n
 s
s
n 2
2 
 
4
2
2 2
2
2




 s
s
s
s n
n 

5
0.

 
1

 n

17

18. Problem 2

20. Problem 3

28. Static error constant for various type number
of system

29. Steady state error for various types of input

36. Problem 4

37. Problem 5

53. References :
 A.Nagoorkani, Control Systems,
RBA Publications.
4/5/2021 53

54. Thank You
54