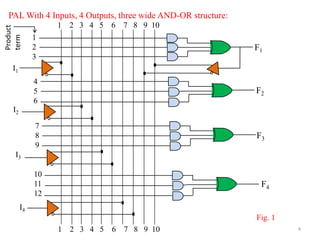
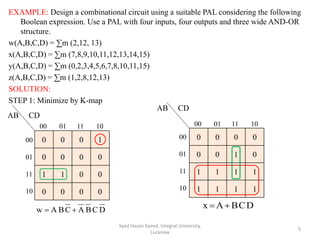
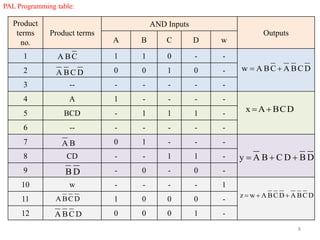
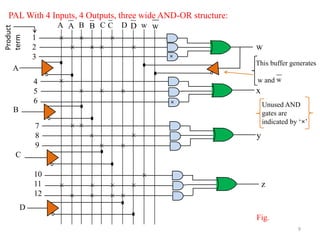
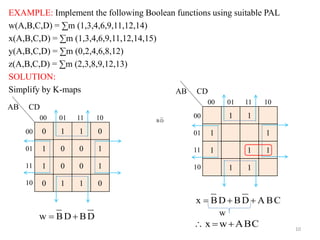
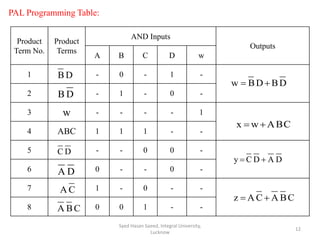
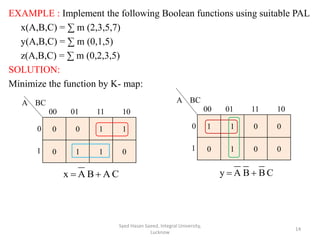
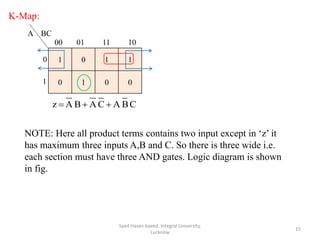
This document describes Programmable Array Logic (PAL) and provides examples of designing combinational logic circuits using PALs. It begins by defining PALs as programmable logic devices with programmable AND gates followed by fixed OR gates. Examples are then given to show how to design PALs with different numbers of inputs and outputs to implement Boolean functions. K-maps are used to minimize the functions before programming the PAL tables. Diagrams of the PAL structures are also shown for examples with 2-wide and 3-wide AND-OR configurations.

1. SYED HASAN SAEED
hasansaeedcontrol@gmail.com
https://shasansaeed.yolasite.com
1
Syed Hasan Saeed, Integral University,
Lucknow

2. PROGRAMMABLE ARRAY LOGIC (PAL)
Syed Hasan Saeed, Integral University,
Lucknow
2

3. PROGRAMMABLE ARRAY LOGIC (PAL):
• The PAL is a programmable logic device with programmable AND gates
followed by fixed OR gates.
• For designing of PAL, the Boolean function must be in simplified form.
• Product term cannot be shared with two or more OR gates, it means that
each function can be simplified by itself.
Syed Hasan Saeed, Integral University,
Lucknow
3

4. PAL With 4 Inputs, 4 Outputs, three wide AND-OR structure:
4
F1
F2
F3
F4
1 2 3 4 5 6 7 8 9 10
1
2
3
4
5
6
7
8
9
10
11
12
1 2 3 4 5 6 7 8 9 10
Product
term
I1
I2
I3
I4
Fig. 1

5. EXAMPLE: Design a combinational circuit using a suitable PAL considering the following
Boolean expression. Use a PAL with four inputs, four outputs and three wide AND-OR
structure.
w(A,B,C,D) = ∑m (2,12, 13)
x(A,B,C,D) = ∑m (7,8,9,10,11,12,13,14,15)
y(A,B,C,D) = ∑m (0,2,3,4,5,6,7,8,10,11,15)
z(A,B,C,D) = ∑m (1,2,8,12,13)
SOLUTION:
STEP 1: Minimize by K-map
Syed Hasan Saeed, Integral University,
Lucknow
5
0 0 0 1
0 0 0 0
1 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
1 1 1 1
1 1 1 1
AB CD
AB CD
00 01 11 10 00 01 11 10
00
01
11
10
00
01
11
10
DCBACBAw 
DCBAx 

6. K-maps
Syed Hasan Saeed, Integral University,
Lucknow
6
1 1
1 1
1
AB CD
00 01 11 10
00
01
11
10
1 0 1 1
1 1 1 1
0 0 1 0
1 0 1 1
AB CD
00 01 11 10
00
01
11
10
DBDCBAy 
DCBADCBADCBACBAz 
w
DCBADCBAwz 

7. • Given that
• Input = 4 , Output =4 and three wide AND-OR structure, it means
each output expression must contain at most three product terms.
• In z , there are four product terms, we can reduced to three by
substituting in the expression of z.
• The output ‘w’ and ‘x’ having two terms. So one AND gate of w
and x will remain unused. For unused AND gates, leave all its input
fuse intact (always = 0)
Syed Hasan Saeed, Integral University,
Lucknow
7
DCBACBAw 

8. PAL Programming table:
8
Product
terms
no.
Product terms
AND Inputs
Outputs
A B C D w
1 1 1 0 - -
2 0 0 1 0 -
3 -- - - - - -
4 A 1 - - - -
5 BCD - 1 1 1 -
6 -- - - - - -
7 0 1 - - -
8 CD - - 1 1 -
9 - 0 - 0 -
10 w - - - - 1
11 1 0 0 0 -
12 0 0 0 1 -
DCBADCBAwz 
DCBACBAw 
DCBAx 
CBA
DCBA
BA
DCBA
DCBA
DBDCBAy 
DB

9. PAL With 4 Inputs, 4 Outputs, three wide AND-OR structure:
9
w
x
y
z
A B C D w
1
2
3
4
5
6
7
8
9
10
11
12
Product
term
A
B
C
D
Fig.
×
×
Unused AND
gates are
indicated by ‘×’
w
This buffer generates
w and w
× × ×
A B C D
× × × ×
×
× × ×
× ×
× ×
××
×
× × × ×
× × × ×

10. EXAMPLE: Implement the following Boolean functions using suitable PAL
w(A,B,C,D) = ∑m (1,3,4,6,9,11,12,14)
x(A,B,C,D) = ∑m (1,3,4,6,9,11,12,14,15)
y(A,B,C,D) = ∑m (0,2,4,6,8,12)
z(A,B,C,D) = ∑m (2,3,8,9,12,13)
SOLUTION:
Simplify by K-maps
10
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0
AB CD
00 01 11 10
00
01
11
10
1 1
1 1
1 1 1
1 1
AB CD
00 01 11 10
00
01
11
10
DBDBw 
CBADBDBx 
DB
w
CBAwx 

11. K-maps:
Syed Hasan Saeed, Integral University,
Lucknow
11
1 0 0 1
1 0 0 1
1 0 0 0
1 0 0 0
AB CD
00 01 11 10
00
01
11
10
0 0 1 1
0 0 0 0
1 1 0 0
1 1 0 0
AB CD
00 01 11 10
00
01
11
10
DADCy  CBACAz 

12. PAL Programming Table:
Syed Hasan Saeed, Integral University,
Lucknow
12
Product
Term No.
Product
Terms
AND Inputs
Outputs
A B C D w
1 - 0 - 1 -
2 - 1 - 0 -
3 w - - - - 1
4 ABC 1 1 1 - -
5 - - 0 0 -
6 0 - - 0 -
7 1 - 0 - -
8 0 0 1 - -
DB
DB
DA
DC
CBA
CA
DBDBw 
CBAwx 
DADCy 
CBACAz 

13. PAL With 4 Inputs, 4 Outputs, two wide AND-OR structure:
13
w
x
y
z
A B C D w
1
2
3
4
5
6
7
8
Product
term
A
B
C
D
Fig.
w
This buffer generates
w and w
× ×
A B C D
× ×
×
× ××
× ×
× ×
×
× ×
×
×

14. EXAMPLE : Implement the following Boolean functions using suitable PAL
x(A,B,C) = ∑ m (2,3,5,7)
y(A,B,C) = ∑ m (0,1,5)
z(A,B,C) = ∑ m (0,2,3,5)
SOLUTION:
Minimize the function by K- map:
Syed Hasan Saeed, Integral University,
Lucknow
14
0 0 1 1
0 1 1 0
A BC
00 01 11 10
0
1
1 1 0 0
0 1 0 0
A BC
00 01 11 10
0
1
CABAx  CBBAy 

15. K-Map:
Syed Hasan Saeed, Integral University,
Lucknow
15
1 0 1 1
0 1 0 0
A BC
00 01 11 10
0
1
CBACABAz 
NOTE: Here all product terms contains two input except in ‘z’ it
has maximum three inputs A,B and C. So there is three wide i.e.
each section must have three AND gates. Logic diagram is shown
in fig.

16. PAL With 4 Inputs, 4 Outputs, three wide AND-OR structure:
16
x
y
z
A B C D
1
2
3
4
5
6
7
8
9
Product
term
A
B
C
D
Fig.
× Unused AND
gates are
indicated by ‘×’
A B C D
× ×
× ×
× ×
× ×
××
× ×
× × ×
×

17. THANK YOU
Syed Hasan Saeed, Integral University,
Lucknow
17