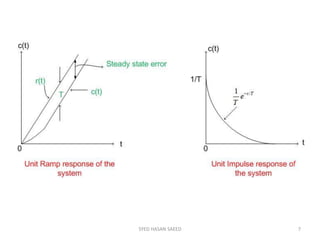
This document discusses the time response of a first order system to different input functions. It describes how a first order system responds to a unit step input, with the output reaching 63.2% of its final value after one time constant. For a unit ramp input, the steady state error is equal to the time constant. For a unit impulse input, the output is an exponential decay that returns the system to its initial state. The responses are related as the unit step is the derivative of the ramp, and the impulse is the derivative of the step, demonstrating the property of linear time-invariant systems.

1. TIME RESPONSE
OF
FIRST ORDER SYSTEM
Email : hasansaeedcontrol@gmail.com
URL: http://shasansaeed.yolasite.com/
1SYED HASAN SAEED

2. RESPONSE OF FIRST ORDER SYSTEM WITH UNIT STEP
INPUT:
For first order system
SYED HASAN SAEED 2
sT
T
s
sC
sTs
sC
s
sR
sR
sT
sC
sTsR
sC









1
1
)(
)1(
1
)(
1
)(
)(
1
1
)(
1
1
)(
)(
Input is unit step
After partial fraction

3. Take inverse Laplace
Where ‘T’ is known as ‘time constant’ and defined as
the time required for the signal to attain 63.2% of
final or steady state value.
Time constant indicates how fast the system reaches
the final value.
Smaller the time constant, faster is the system
response.
SYED HASAN SAEED 3
632.011)(
1)(
1/
/




eetc
etc
TT
Tt
When t=T

4. RESPONSE OF FIRST ORDER SYSTEM WITH UNIT RAMP
FUNCTION:
SYED HASAN SAEED 4
T
s
T
s
T
s
sC
sTs
sC
s
sR
sR
sT
sC
sTsR
sC
1
11
)(
)1(
1
)(
1
)(
)(
1
1
)(
1
1
)(
)(
2
2
2









Input is unit Ramp
After partial fraction
We know that

5. Take inverse Laplace, we get
The steady state error is equal to ‘T’, where ‘T’ is the
time constant of the system.
For smaller time constant steady state error will be
small and speed of the response will increase.
SYED HASAN SAEED 5
 
TTeTLimit
eTte
TeTttte
tctrte
TeTttc
Tt
t
Tt
Tt
Tt










)(
)1()(
)(
)()()(
)(
/
/
/
/
Error signal
Steady state error

6. RESPONSE OF THE FIRST ORDER SYSTEM WITH UNIT
IMPULSE FUNCTION:
Input is unit impulse function R(s)=1
SYED HASAN SAEED 6
Tt
e
T
tc
TsT
sC
sT
sC
sR
sT
sC
/1
)(
/1
11
)(
1.
1
1
)(
)(
1
1
)(








Inverse Laplace transform

7. SYED HASAN SAEED 7

8. SYED HASAN SAEED 8
1)(
1
)(
1
)( 2



sR
s
sR
s
sRFor unit Ramp Input
For Unit Step Input
For Unit Impulse Input
Tt
TeTttc /
)( 

Tt
etc /
1)( 

Tt
e
T
tc /1
)( 

It is clear that, unit step input is the derivative of unit
ramp input and unit impulse input is the derivative of
unit step input. This is the property of LTI system.
Compare all three responses:

9. THANK YOU
SYED HASAN SAEED 9