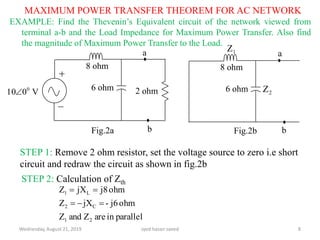
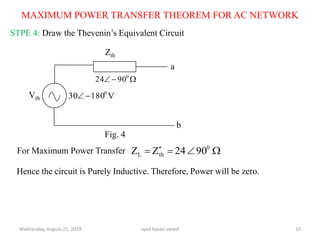
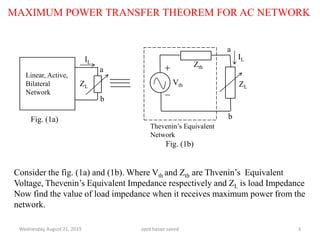
This document discusses the maximum power transfer theorem for AC networks. It defines the theorem as stating that maximum power is transferred from an AC network to a load when the load impedance is equal to the complex conjugate of the Thevenin's equivalent impedance of the network. It provides examples of calculating the Thevenin's equivalent circuit for a given network and determining the load impedance required for maximum power transfer. In the example network shown, the Thevenin's equivalent impedance is found to be purely inductive, meaning no power can be transferred to the load.

1. CIRCUIT THEORY
MAXIMUM POWER TRANSFER THEOREM
FOR
AC NETWORK
Wednesday, August 21, 2019 1syed hasan saeed
SYED HASAN SAEED

2. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
REFERENCE BOOKS
• Introductory Circuit Analysis, Robert L. Boylested, Pearson Education,
Prentice Hall.
• Networks And Systems, Ashfaq Husain, Khanna Book Publishing Co (P)
Ltd. Delhi.
• Networks And Systems, A Sudhakr, Shyammohan S Palli, Tata McGraw
Hill, New Delhi.
• Network Analysis, M.E. Van Valkenburg, PHI Learning Private limited,
New Delhi.
• Circuit Analysis Principle and Applications, Allan H. Robbins &Wilhelm
C. Miller, DELMAR CENGAGE Learning, Indian Reprint.
Wednesday, August 21, 2019 syed hasan saeed 2

3. Wednesday, August 21, 2019 syed hasan saeed 3
Vth
Zth
Linear, Active,
Bilateral
Network
a
b
b
a
IL
IL
Thevenin’s Equivalent
Network
Fig. (1a)
Fig. (1b)
ZL ZL
MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
Consider the fig. (1a) and (1b). Where Vth and Zth are Thvenin’s Equivalent
Voltage, Thevenin’s Equivalent Impedance respectively and ZL is load Impedance
Now find the value of load impedance when it receives maximum power from the
network.

4. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
PROOF:
Wednesday, August 21, 2019 syed hasan saeed 4
2
Lth
2
Lth
th
L
LthLth
th
L
Lth
th
L
LLL
ththth
)X(X)R(R
V
I
)X(Xj)R(R
V
I
ZZ
V
I
jXRZ
jXRZ








Power Transferred to the load is
-(1)-------
)X(X)R(R
RV
RIP 2
Lth
2
Lth
L
2
th
L
2
LL



5. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
For any network Vth, Rth and Xth are fixed.
CASE 1: When RL is constant and XL is varying:
Wednesday, August 21, 2019 syed hasan saeed 5
 
 
 
(2)-----------X-X
0X2(XRV-
0
)X(X)R(R
X2(XRV-[0])X(X)R(R
dX
dP
0
)X(X)R(R
RV
dX
d
dX
dP
thL
ththL
2
th
22
Lth
2
Lth
LthL
2
th
2
Lth
2
Lth
L
L
2
Lth
2
Lth
L
2
th
LL
L














Hence, the magnitude of load reactance must be equal Thevenin’s reactance but
opposite phase difference. This is the first condition. The equation (1) becomes
)3(
)R(R
RV
P 2
Lth
L
2
th
L 



6. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
CASE 2: When XL is constant and RL is varying
Wednesday, August 21, 2019 syed hasan saeed 6
 
 
 
(4)-------R)X(XR
0)R2(RRV-][V)X(X)R(R
0
)X(X)R(R
)R2(RRV-][V)X(X)R(R
dX
dP
0
)X(X)R(R
RV
dR
d
dR
dP
L
2
Lth
2
th
LthL
2
th
2
th
2
Lth
2
Lth
22
Lth
2
Lth
LthL
2
th
2
th
2
Lth
2
Lth
L
L
2
Lth
2
Lth
L
2
th
LL
L














Put Xth = -XL in equation (4)
RL = Rth - - - - - - - - - - - - - - - (5)
Hence, for maximum Power Transfer, the load resistance must be equal to the
Thevenin’s Equivalent Resistance. The equation (3) becomes
)6(
4R
V
P
th
2
th
maxL 

7. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
CASE 3: Apply equation (2) and (5) simultaneously then
Wednesday, August 21, 2019 syed hasan saeed 7

 thththLLL ZXjRXjRZ
Hence, Maximum Power Transfer Theorem states the “Maximum Power is
transferred from AC network to the load when Load Impedance is equal to the
complex conjugate of Thevenin’s Equivalent Impedance”

8. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
EXAMPLE: Find the Thevenin’s Equivalent circuit of the network viewed from
terminal a-b and the Load Impedance for Maximum Power Transfer. Also find
the magnitude of Maximum Power Transfer to the Load.
Wednesday, August 21, 2019 syed hasan saeed 8
V010 0

8 ohm
6 ohm 2 ohm
a
bFig.2a
STEP 1: Remove 2 ohm resistor, set the voltage source to zero i.e short
circuit and redraw the circuit as shown in fig.2b
STEP 2: Calculation of Zth
parallelinareZandZ
ohmj6-jXZ
ohmj8jXZ
21
C2
L1


8 ohm
6 ohm
b
a
Fig.2b
1Z
2Z

9. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
Wednesday, August 21, 2019 syed hasan saeed 9









0
0
0
th
0
00
21
21
th
9024
902
048
Z
902
)906)(90(8
ZZ
ZZ
z
STEP 3: Calculation of Thevenin’s Equivalent voltage Vth
8 ohm
6 ohm
a
b
V010 0
 Vth
Apply KVL in mesh (1)
I
V18030V
)90-(-j6)(5IZV
A905
902
010
I
j2I010
0j6Ij8I-010
0
th
0
2th
0
0
0
0
0








Fig. 3
-j6 ohm
j8 ohm

10. MAXIMUM POWER TRANSFER THEOREM FOR AC NETWORK
STPE 4: Draw the Thevenin’s Equivalent Circuit
Hence the circuit is Purely Inductive. Therefore, Power will be zero.
Wednesday, August 21, 2019 syed hasan saeed 10
Vth
Zth
V18030 0

 0
9024
a
b
Fig. 4
For Maximum Power Transfer  
9024ZZ 0
thL

11. Wednesday, August 21, 2019 syed hasan saeed 11
THANK YOU
hasansaeedcontrol@gmail.com
shasansaeed@yolasite.com
hasansaeed872726549.wordpress.com
saeed.moodlecloud.com
syedhasansaeed.gnomio.com