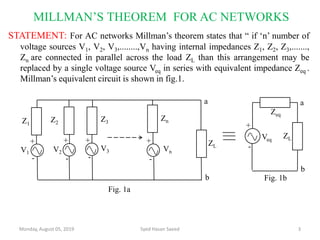
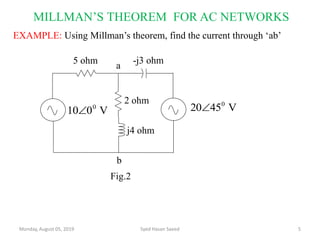
This document discusses Millman's theorem for AC networks. It states that multiple voltage sources in parallel with internal impedances can be replaced by an equivalent single voltage source in series with an equivalent impedance. The equivalent voltage and impedance are calculated using the individual voltage and admittance values. An example problem demonstrates how to use the theorem to find the current through a load for a given parallel AC circuit. Reference books on circuit analysis are also listed.

1. CIRCUIT THEORY
MILLMAN’S THEOREM
FOR
AC NETWORKS
SYED HASAN SAEED
Monday, August 05, 2019 1Syed Hasan Saeed

2. REFERENCE BOOKS
• Introductory Circuit Analysis, Robert L. Boylested, Pearson Education,
Prentice Hall.
• Networks And Systems, Ashfaq Husain, Khanna Book Publishing Co (P)
Ltd. Delhi.
• Networks And Systems, A Sudhakr, Shyammohan S Palli, Tata McGraw
Hill, New Delhi.
• Network Analysis, M.E. Van Valkenburg, PHI Learning Private limited,
New Delhi.
• Circuit Analysis Principle and Applications, Allan H. Robbins &Wilhelm
C. Miller, DELMAR CENGAGE Learning, Indian Reprint.
Monday, August 05, 2019 syed hasan saeed 2

3. MILLMAN’S THEOREM FOR AC NETWORKS
STATEMENT: For AC networks Millman’s theorem states that “ if ‘n’ number of
voltage sources V1, V2, V3,........,Vn having internal impedances Z1, Z2, Z3,.......,
Zn are connected in parallel across the load ZL than this arrangement may be
replaced by a single voltage source Veq in series with equivalent impedance Zeq .
Millman’s equivalent circuit is shown in fig.1.
Monday, August 05, 2019 Syed Hasan Saeed 3
⁓
Z1
Z2 Z3
Zn
ZL
V1 V2
V3 Vn
Zeq
ZLVeq+ + + +
+
- - - -
-
Fig. 1a
Fig. 1b
a
b
a
b

4. MILLMAN’S THEOREM FOR AC NETWORKS
Monday, August 05, 2019 Syed Hasan Saeed 4
)2(
YYYY
1
Z
)1(
YYYY
YVYVYVYV
V
n321
eq
n321
nn332211
eq







Z
1
Y
es.admitatanctheareY,.......Y,Y,YandimpedancestheareZ.......Z,Z,ZWhere n321n321

This theorem is applicable only to solve the parallel branch with one impedance or
resistance connected to voltage or current source. The voltage sources can be
converted into current sources by transformation of sources.

5. MILLMAN’S THEOREM FOR AC NETWORKS
EXAMPLE: Using Millman’s theorem, find the current through ‘ab’
Monday, August 05, 2019 Syed Hasan Saeed 5
5 ohm
2 ohm
-j3 ohm
j4 ohm
V010 0
 V4520 0

a
b
Fig.2

6. MILLMAN’S THEOREM FOR AC NETWORKS
SOLUTION:
Monday, August 05, 2019 Syed Hasan Saeed 6
V4520V
V010V
0
2
0
1


S900.33
j3-
1
Z
1
Y
S0.2
5
1
Z
1
Y
0
2
1
1
1












0
0
eq
eq
0
eq
0
000
eq
21
2211
eq
58.78-2.59
900.330.2
1
Y
1
Z
V60.9713.94V
900.330.2
90(0.33)45(20(0.2))0(10
V
YY
YVYV
V

7. MILLMAN’S THEOREM FOR AC NETWORKS
Monday, August 05, 2019 Syed Hasan Saeed 7
Millman’s Equivalent Circuit:
2 ohm
j4 ohm
eqZ
 0
58.78-2.59
V60.9713.94 0
eqV
+
-
A32.793.68I
j4)(258.78)-(2.59
60.9713.94
j4)(2Z
V
I
0
ab
0
eq
eq
ab






Fig. 3
a
b
Current through branch ab A32.793.68 0


8. Monday, August 05, 2019 syed hasan saeed 8
THANK YOU
hasansaeedcontrol@gmail.com
shasansaeed@yolasite.com
hasansaeed872726549.wordpress.com
saeed.moodlecloud.com
syedhasansaeed.gnomio.com