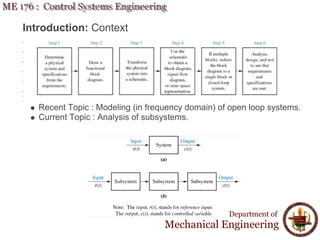
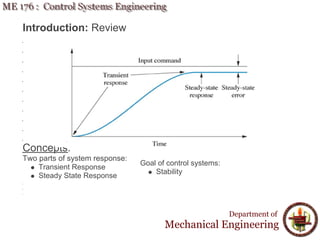
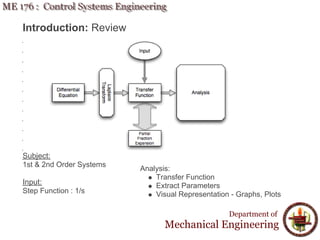
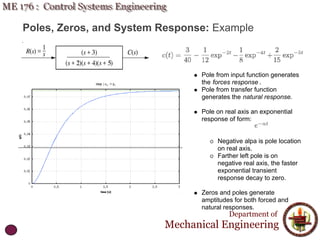
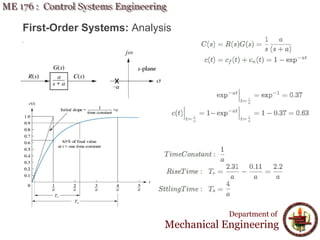
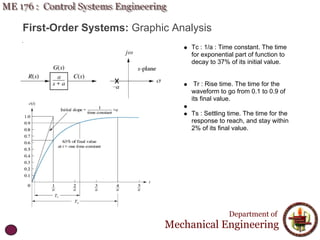
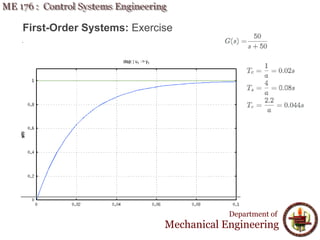
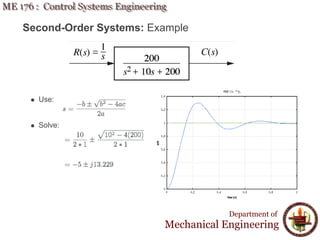
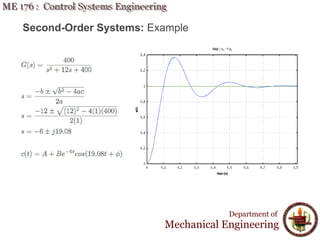
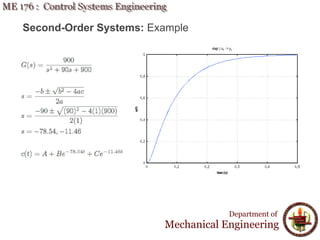
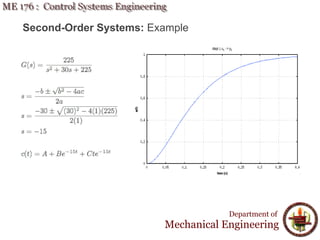
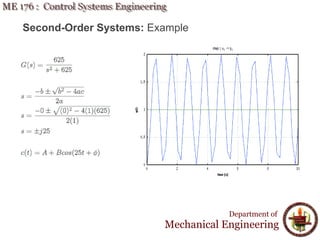
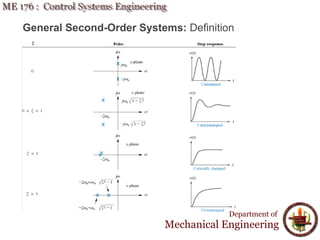
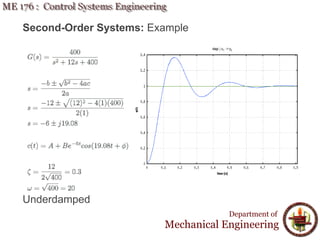
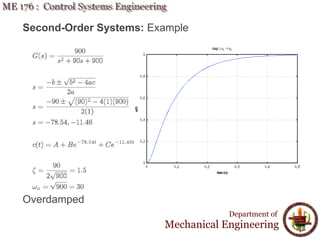
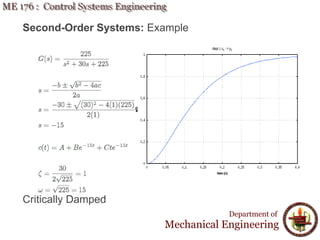
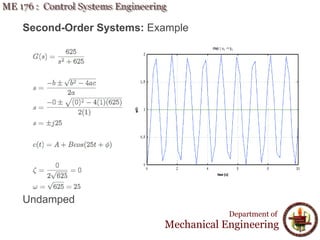
This document discusses time response analysis of control systems. It covers topics such as first-order and second-order systems, including their poles, zeros, and responses. For first-order systems, it describes concepts like time constant, rise time, and settling time. It then covers different types of responses for second-order systems, including overdamped, underdamped, undamped, and critically damped. Examples are provided to illustrate these concepts and analyze systems from their transfer functions.

1. ME 176
Control Systems Engineering
Department of
Mechanical Engineering
Time Response

2. Introduction: Context
Recent Topic : Modeling (in frequency domain) of open loop systems.
Current Topic : Analysis of subsystems.
Department of
Mechanical Engineering

3. Introduction: Review
Concepts:
Two parts of system response:
Transient Response
Steady State Response
Department of
Mechanical Engineering
Goal of control systems:
Stability

4. Introduction: Review
Subject:
1st & 2nd Order Systems
Input:
Step Function : 1/s
Department of
Mechanical Engineering
Analysis:
Transfer Function
Extract Parameters
Visual Representation - Graphs, Plots

5. Department of
Mechanical Engineering
Poles, Zeros, and System Response: Definition
Poles
Values of the Laplace Transform variable, s, that causes the transfer function
to become infinite.
Roots of the denominator of transfer function that are common to roots of the
numerator.
Zeros
Values of the Laplace Transform variable, s, that causes the transfer function
to become zero.
Roots of the denominator of transfer function that are common to roots of the
numerator.
System Response
Natural Response (Homogeneous Solution) - describes the way the system
dissipates or acquires energy; dependent on the system.
Forced Response (Particular Solution) - based on the input into the system.

6. Poles, Zeros, and System Response: Identify Parts
Department of
Mechanical Engineering

7. Poles, Zeros, and System Response: Concepts
Department of
Mechanical Engineering
Forced Response
Natural Response

8. Poles, Zeros, and System Response: Example
Department of
Mechanical Engineering
Pole from input function generates
the forces response .
Pole from transfer function
generates the natural response.
Pole on real axis an exponential
response of form:
Negative alpa is pole location
on real axis.
Farther left pole is on
negative real axis, the faster
exponential transient
response decay to zero.
Zeros and poles generate
amptitudes for both forced and
natural responses.

9. First-Order Systems: Analysis
Department of
Mechanical Engineering

10. First-Order Systems: Graphic Analysis
Department of
Mechanical Engineering
Tc : 1/a : Time constant. The time
for exponential part of function to
decay to 37% of its initial value.
Tr : Rise time. The time for the
waveform to go from 0.1 to 0.9 of
its final value.
Ts : Settling time. The time for the
response to reach, and stay within
2% of its final value.

11. First-Order Systems: Exercise
Department of
Mechanical Engineering

12. Second-Order Systems: Analysis
Use general equation of the following form:
Use quadratic equation to get roots:
Use step function as input.
Exhibit wide variety of responses - system parameters not just change speed
but form of responses.
Types of 2nd order transient responses:
Overdamped
Underdamped
Undamped
Critically damped
Department of
Mechanical Engineering

13. Second-Order Systems: Overdamped Systems
Poles : two real.
Natural Response : two exponentials with time constants equal to the
reciprocal of the pole locations:
Department of
Mechanical Engineering

14. Second-Order Systems: Underdamped Systems
Poles : two complex.
Natural Response : damped sinusoid with exponential envelope whose time
constant is equal to the reciprocal of the pole's real part. The radian frequency
of the sinusoid, the damped frequency oscillation, is equal to imaginary part of
the poles:
Department of
Mechanical Engineering

15. Second-Order Systems: Undamped Systems
Poles : two imaginary.
Natural Response : undamped sinusoid with radian frequency equal to
imaginary part of the poles:
Department of
Mechanical Engineering

16. Second-Order Systems: Critically damped Systems
Poles : two real.
Natural Response : one term is an exponential whose time constant is equal to
the reciprocal of the pole location. Another term is the product of time, t, and
the exponential with time constant equal to the reciprocal of the pole location:
Department of
Mechanical Engineering

17. Second-Order Systems: Example
Use:
Solve:
Department of
Mechanical Engineering

18. Second-Order Systems: Example
Department of
Mechanical Engineering

19. Second-Order Systems: Example
Department of
Mechanical Engineering

20. Second-Order Systems: Example
Department of
Mechanical Engineering

21. Second-Order Systems: Example
Department of
Mechanical Engineering

22. General Second-Order Systems: Definition
Natural Frequency : is the frequency of oscillation of the system
without damping.
Damping Ratio : is the ration of the exponential decay frequency of
the envelope to the natural frequency.
Department of
Mechanical Engineering

23. General Second-Order Systems: Definition
Department of
Mechanical Engineering

24. Second-Order Systems: Example
Underdamped
Department of
Mechanical Engineering

25. Second-Order Systems: Example
Overdamped
Department of
Mechanical Engineering

26. Second-Order Systems: Example
Critically Damped
Department of
Mechanical Engineering

27. Second-Order Systems: Example
Undamped
Department of
Mechanical Engineering

28. Quiz: For the transfer functions below, find the location of the poles and
zeros, plot them on the s-plane, and then write an expressions for the
general form of the step response without solving for the inverse Laplace
transform. State the nature of each response:
Department of
Mechanical Engineering