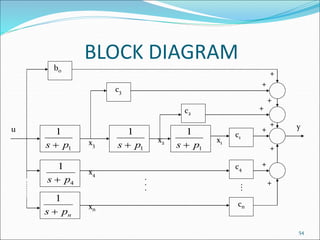
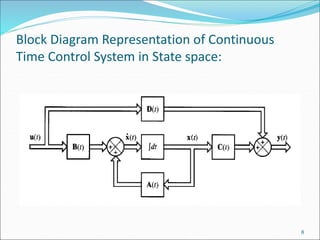
This document discusses and compares the classical/transfer function approach and the state space/modern control approach for modeling dynamical systems. The classical approach uses Laplace transforms and transfer functions in the frequency domain, while the state space approach uses matrices to represent systems of differential equations directly in the time domain. The state space approach can model nonlinear, time-varying, and multi-input multi-output systems and considers initial conditions, while the classical approach is limited to linear time-invariant single-input single-output systems. The document provides examples of modeling circuits using the state space representation.

1. Dr. K Hussain
Associate Professor and Head
Dept. of Electrical Engineering
SITCOE

2. Advantages of State Space Approach
Classical/Transfer function
Approach
State space approach/Modern
Control Approach
 Transfer Function Approach
 Linear Time Invariant System,
SISO
 Laplace Transform, Frequency
domain
 Only Input-output Description:
Less Detail Description on System
Dynamics
 Doesn’t take all ICs
 Taking specific inputs like step,
ramp and parabolic etc…
 State Variable Approach
 Linear Time Varying, Nonlinear,
Time Invariant, MIMO
 Time domain
 Detailed description of Internal
behaviour in addition to I-O
properties
 Consider all ICs
 Taking all inputs
2

3. CLASSICAL APPROACH (TRANSFER FUNCTION)
 The classical approach or frequency domain
technique is based on converting a system’s
differential equation to a transfer function.
 It relates a representation of the output to a
representation of the input.
 It can be applied only to linear, time-invariant
systems.
 It rapidly provides stability and transient response
information.
3

4.  The state-space approach (also referred to as the modern, or
time-domain, approach) is a unified method for modeling,
analyzing, and designing a wide range of systems.
 The state-space approach can be used to represent nonlinear
systems. Also, it can handle, conveniently, systems with
nonzero initial conditions and time varying.
 The state-space approach is also attractive because of the
availability of numerous state-space software package for the
personal computer.
MODERN APPROACH (STATE-SPACE)
4

5. MODERN APPROACH (STATE-SPACE)
 It can be used to model and analyze nonlinear
(backlash, saturation), time-varying (missiles with
varying fuel levels), multi-input multi-output
systems (i.e., an airplane) with nonzero initial
conditions.
 But it is not as intuitive as the classical approach.
The designer has to engage in several calculations
before the physical interpretation of the model is
apparent.
5

6. STATE-SPACE REPRESENTATION
 Select a particular subset of all possible system
variables and call them state variables.
 For an nth-order system, write n simultaneous
first-order differential equations in terms of state
variables.
 If we know the initial conditions of all state
variables at t0 and the system input for tt0, we can
solve the simultaneous differential equations for
the state variables for tt0.
6

7. Concept of State Variables
 State: The state of a dynamic system is the smallest set of
variables (called state variables) so that the knowledge of
these variables at t = t0, together with the knowledge of the
input for t  t0, determines the behavior of the system for any
time t  t0.
 State Variables: The state variables of a dynamic system are
the variables making up the smallest set of variables that
determine the state of the dynamic system.
 State Vector: If n state variables are needed to describe the
behavior of a given system, then the n state variables can be
considered the n components of a vector x. Such vector is
called a state vector.
 State Space: The n-dimensional space whose coordinates
axes consist of the x1 axis, x2 axis, .., xn axis, where x1, x2, .., xn
are state variables, is called a state space.
7

8. Block Diagram Representation of Continuous
Time Control System in State space:
8

9. Time Varying/Invariant Systems
9
Time Varying System:
Time Invariant System:

10. State & Output Equation:
Matrices/Vectors
10
A(t)= State/System Matrix
B(t)= Input Matrix
C(t)=Output Matrix
D(t)=Direct Transmission Matrix

11. The general form of state and output equations for a linear,
time-invariant system can be written as
Du+Cx=yBu+Ax=x
Where x is the n x 1 state vector,
u is r x 1 input vector,
y is the m x 1 output vector,
A is nxn System Matrix,
B is nxr Input Matrix,
C is mxn Output Matrix and
D is mxr Transition Matrix. 11

12. RLC Circuit
12

13. 13

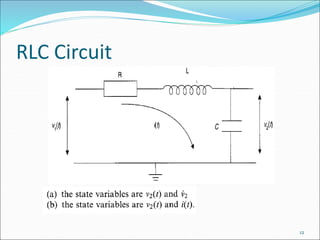
14. EXAMPLE:
+ i(t)
Lv(t)
R
L
di
dt
Ri v t
v t Ri t
 

( )
( ) ( ) ( )
(state equation)
Output equation
tLRtLR
L
R
L
R
eie
R
ti
s
i
ssR
sI
sVissIL
)/()/(
)0()1(
1
)(
)0(111
)(
)()]0()([












Assuming that v(t) is a unit step and knowing i(0), taking the LT of the state
equation
14

15. Writing the equations in matrix-vector form


i
v 0
i
v 0
v(t)
c
R
L
1
L
1
C c
1
L




 
 












 






Assuming the voltage across the resistor as the output
 v (t) Ri(t) R 0
i
vR
c
 






15

16. Example: Given the electric network, find a state-space representation.
(Hint: state variables and , output )Cv Li
)(
/1
0
0/1
/1)/(1
tv
Li
v
L
CRC
i
v
L
C
L
C




























  






L
C
R
i
v
Ri 0/1
Ri
  0=D;0R=C
;
0
=B;
0
--
=A;
v
i
=x L
R
1
L
1
L
R
c


















C
16

17. 17

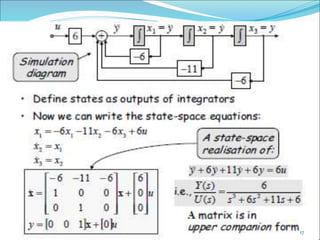
18. Transfer function From State space :
DuCxy
BuAxx


Given the state and output equations
Take the Laplace transform assuming zero initial conditions:
(1)
(2)
Solving for in Eq. (1),
or
(3)
Substitutin Eq. (3) into Eq. (2) yields
The transfer function is
)()()(
)()()(
sss
ssss
DUCXY
BUAXX


)(sX
)()()( sss BUXAI 
)()()( 1
sss BUAIX 

)()()()( 1
ssss DUBUAICY  
)(])([ 1
ss UDBAIC  
DBAIC
U
Y
 1
)(
)(
)(
s
s
s
18

19. Ex. Find the transfer from the state-space representation
u























0
0
10
321
100
010
xx
 x001y





































321
10
01
321
100
010
00
00
00
)(
s
s
s
s
s
s
s AI
Solution:
123
12
31
1323
)det(
)(
)( 23
2
2
2
1

















 
sss
sss
sss
sss
s
sadj
s
AI
AI
AI
123
)23(10
)(
)(
23
2



sss
ss
s
s
U
Y
19

20. Solution of State Equations:
20

21. 21

22. 22

23. State Transition Matrix
23

24. Laplace Transform Method (STM Computation)
24

25. 25

26. Total Response
26

27. Natural Modes
27

28. Diagonalization
28

29. 29

30. 30

31. STATE SPACE REPRESENTATION OF DYNAMIC
SYSTEMS
Consider the following n-th order differential equation in which the forcing
function does not involve derivative terms.
d y
dt
a
d y
dt
a
dy
dt
a y b u
Y s
U s
b
s a s a s a
n
n
n
n n n
n n
n n
    

   

 


1
1
1 1 0
0
1
1
1


( )
( )
Choosing the state variables as
x y, x y, x y, , x
d y
dt
x x , x x , ,x x
x a x a x a x b u
1 2 3 n
n 1
n 1
1 2 2 3 n-1 n
n n 1 n 1 2 1 n 0
   
  
     



 
  




31

32. 





x
x
x
x
x
x
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
a a a a a
x
x
x
x
x
x
1
2
3
n 2
n 1
n n n 1 n 2 2 1
1
2
3
n 2
n 1
n




 



 

























    



































































0
0
0
0
0
b
u
y = [1 0 0 0 0]x
0


32

33. State Space Representation of system with
forcing function involves Derivatives
Consider the following n-th order differential equation in
which the forcing function involves derivative terms.
d y
dt
a
d y
dt
a
dy
dt
a y
b
d u
dt
b
d u
dt
b
du
dt
b u
Y s
U s
b s b s b s b
s a s a s a
n
n
n
n n n
n
n
n
n n n
n n
n n
n n
n n
   
    

   
   

 

 




1
1
1 1
0 1
1
1 1
0 1
1
1
1
1
1




( )
( )
33

34. Define the following n variables as a set of n state variables
uxu
dt
du
dt
ud
dt
ud
dt
yd
x
uxuuuyx
uxuuyx
uyx
nnnnn
n
n
n
n
n
n 11122
2
11
1
0
222103
11102
01
















34

35. 

.
.
.


. . . .
. . . .
. . . .
.
.
.
.
.
.
x
x
x
x a a a a
x
x
x
x
n
n n n n
n
n
n
1
2
1
1 2 1
1
2
1
1
2
1
0 1 0 0
0 0 1 0
0 0 0 1
 
 























   




















































 


n
n
u
y
x
x
x
u









































1 0 0
1
2
0
.
.
.
35

36. CONTROLLABLE CANONICAL FORM
d y
dt
a
d y
dt
a
dy
dt
a y
b
d u
dt
b
d u
dt
b
du
dt
b u
Y s
U s
b s b s b s b
s a s a s a
n
n
n
n n n
n
n
n
n n n
n n
n n
n n
n n
   
    

   
   

 

 




1
1
1 1
0 1
1
1 1
0 1
1
1
1
1
1




( )
( )
36

37. Y s
U s
b
b a b s b a b b a b
s a s a s a
Y s b U s Y s
Y s
b a b s b a b b a b
s a s a s a
n
n n n n
n n
n n
n
n n n n
n n
n n
( )
( )
( ) ( ) ( )
( ) ( ) ( )
( )
( ) ( ) ( )
 
     
   
 

     
   

 



 


0
1 1 0
1
1 1 0 0
1
1
1
0
1 1 0
1
1 1 0 0
1
1
1




U s
Y s
b a b s b a b b a b
U s
s a s a s a
Q s
n
n n n n
n n
n n
( )
( )
( ) ( ) ( )
( )
( )
1 1 0
1
1 1 0 0
1
1
1
     

   


 




37

38. s Q s a s Q s a sQ s a Q s U s
Y s b a b s Q s b a b sQ s
b a b Q s
n n
n n
n
n n
n n
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( )
     
    
 



 
1
1
1
1 1 0
1
1 1 0
0


Defining state variables as follows:
X s Q s
X s sQ s
X s s Q s
X s s Q s
n
n
n
n
1
2
1
2
1
( ) ( )
( ) ( )
( ) ( )
( ) ( )








sX s X s
sX s X s
sX s X sn n
1 2
2 3
1
( ) ( )
( ) ( )
( ) ( )







x x
x x
x xn n
1 2
2 3
1




38

39. sX s a X s a X s a X s U s
x a x a x a x u
Y s b U s b a b s Q s b a b sQ s
b a b Q s
b U s b a b X s
n n n n
n n n n
n
n n
n n
n
( ) ( ) ( ) ( ) ( )

( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
( ) ( ) ( )
     
     
     

  



 
1 1 2 1
1 1 2 1
0 1 1 0
1
1 1 0
0
0 1 1 0



+
= 

 

       
 
 
( ) ( )
( ) ( )
( ) ( ) ( )
b a b X s
b a b X s
y b a b x b a b x b a b x b u
n n
n n
n n n n n
1 1 0 2
0 1
0 1 1 1 0 2 1 1 0 0
+
39

40.   ub
x
x
x
babbabbaby
u
x
x
x
x
aaaax
x
x
x
n
nnnn
n
n
nnnn
n
0
2
1
0110110
1
2
1
121
1
2
1
.
.
.
1
0
.
.
.
0
0
.
.
.
1000
....
....
....
0100
0010
.
.
.






























































































































40

41. BLOCK DIAGRAM
u +
b0
+ + +
+ + + +
+
y
+
+
+
+
+
+
+
b1-a1b0 b2-a2b0 bn-1-an-1 b0 bn-an b0
  
a1 a2
an-1 an
xn xn-1
x2 x1
41

42. OBSERVABLE CANONICAL FORM
s Y s b U s s a Y s bU s
s a Y s b U s a Y s b U s
Y s b U s bU s a Y s
b U s a Y s b U s a Y s
X s
n n
n n n n
s
s n n s n n
n s
n n
[ ( ) ( )] [ ( ) ( )]
[ ( ) ( )] ( ) ( )
( ) ( ) [ ( ) ( )]
[ ( ) ( )] [ ( ) ( )]
( ) [
   
    
   
   


 
 
0
1
1 1
1 1
0
1
1 1
1
1 1
1
1
0
1


bU s a Y s X s
X s b U s a Y s X s
X s b U s a Y s X s
X s b U s a Y s
Y s b U s X s
n
n s n
s n n
s n n
n
1 1 1
1
1
2 2 2
2
1
1 1 1
1
1
0
( ) ( ) ( )]
( ) [ ( ) ( ) ( )]
( ) [ ( ) ( ) ( )]
( ) [ ( ) ( )]
( ) ( ) ( )
 
  
  
 
 

 
 

42

43. sX s X s a X s b a b U s
sX s X s a X s b a b U s
sX s X s a X s b a b U s
sX s a X s b a b U s
x a x b
n n n
n n n
n n n n
n n n n
n n
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
 (
   
   
   
   
  

 
  
1 1 1 1 0
1 2 2 2 2 0
2 1 1 1 1 0
1 0
1

n n
n n n n
n n n
n
a b u
x x a x b a b u
x x a x b a b u
y x b u

   
   
 
  

0
2 1 1 1 1 0
1 1 1 1 0
0
)
 ( )
 ( )

43

44. 

.
.
.


. . .
. . . .
. . . .
.
.
.
.
x
x
x
x
a
a
a
a
x
x
x
x
b a b
b a
n
n
n
n
n
n
n n
n n
1
2
1
1
2
1
1
2
1
0
1
0 0 0
1 0 0
0 0
0 0 1



 













































































 
1 0
1 1 0
1
2
00 0 1
b
b a b
u
y
x
x
b u
.
.
.
.
.
.
.









































44

45. BLOCK DIAGRAM
b0
a1an-1
an
+
+
+
+
+
+
+
  
y
u
bn-anb0 bn-1-an-1b0 b1-a1b0
x1
x2 xn-1 xn
45

46. DIAGONAL CANONICAL FORM
Consider that the denominator polynomial involves only
distinct roots. Then,
Y s
U s
b s b s b s b
s p s p s p
b
c
s p
c
s p
c
s p
n n
n n
n
n
n
( )
( ) ( )( ) ( )

   
  
 



 


0 1
1
1
1 2
0
1
1
2
2



where, ci, i=1,2, …, n are the residues corresponding pi
46

47. Y s b U s
c
s p
U s
c
s p
U s
c
s p
X s
s p
U s sX s p X s U s
X s
s p
U s sX s p X s U s
X s
s p
U s sX s p X s U s
n
n
n
n
n n n
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
 



 



   


   


   
0
1
1
2
2
1
1
1 1 1
2
2
2 2 2
1
1
1


47

48. 


( ) ( ) ( ) ( ) ( )
x p x u
x p x u
x p x u
Y s b U s c X s c X s c X s
y c x c x c x b u
n n n
n n
n n
1 1 1
2 2 2
0 1 1 2 2
1 1 2 2 0
  
  
  
    
    



48

49.  


.
.
.

.
.
.
.
.
.
.
.
.
.
.
x
x
x
p
p
p
x
x
x
u
y c c c
x
x
x
b u
n
n
n
n
n
1
2
1
2
1
2
1 2
1
2
0
0
0
1
1
1































































































49

50. BLOCK DIAGRAM
y
u
x1
x2
xn
c1
b0
c2
cn
+
+
+
+
+
1
1s p
1
2s p
1
s pn
50

51. JORDAN CANONICAL FORM
Consider the case where the denominator polynomial involves multiple roots.
Suppose that the pi’s are different from one another, except that the first three are
equal.
Y s
U s
b s bs b s b
s p s p s p s p
Y s
U s
b
c
s p
c
s p
c
s p
c
s p
c
s p
n n
n n
n
n
n
( )
( ) ( ) ( )( ) ( )
( )
( ) ( ) ( )

   
   
 







 


0 1
1
1
1
3
4 5
0
1
1
3
2
1
2
3
1
4
4



51

52. Y s b U s
c
s p
U s
c
s p
U s
c
s p
U s
c
s p
U s
c
s p
U s
X s
c
s p
U s
X s
c
s p
U s
X s
X s s p
X s
c
s p
U s
X s
X
n
n
( ) ( )
( )
( )
( )
( )
( ) ( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( ) ( )
( )
 






 





 




0
1
1
3
2
1
2
3
1
4
4
1
1
1
3
2
2
1
2
1
2 1
3
3
1
2
1
+ 
3 1
4
4
4
1
( )
( ) ( )
( ) ( )
s s p
X s
c
s p
U s
X s
c
s p
U sn
n
n







52

53. sX s p X s X s x p x x
sX s p X s X s x p x x
sX s p X s U s x p x u
sX s p X s U s x p x u
sX s p X s U s xn n n
1 1 1 2 1 1 1 2
2 1 2 3 2 1 2 3
3 1 3 3 1 3
4 4 4 4 4 4
( ) ( ) ( ) 
( ) ( ) ( ) 
( ) ( ) ( ) 
( ) ( ) ( ) 
( ) ( ) ( ) 
      
      
      
      
   

n n n
n n
n n
p x u
Y s b U s c X s c X s c X s c X s
y b u c x c x c x c x
  
     
     
( ) ( ) ( ) ( ) ( ) ( )0 1 1 2 2 3 3
0 1 1 2 2 3 3


53

54. BLOCK DIAGRAM
b0
c3
c2
c1
c4
cn
x3
x2 x1
x4
xn
.
.
.
..
.
1
1s p
1
1s p
1
4s p
1
1s p
1
s pn
u y
+
+
+
+
+
+
+
+
+
54

55. 




. .
.
x
x
x
x
x
p
p
p
p
p
x
x
x
x
x
u
y c c
n n n
1
2
3
4
1
1
1
4
1
2
3
4
1 2
1 0 0 0
0 1
0 0 0 0
0 0
0 0 0
0
0
1
1
1




 

 















































































  

c
x
x
x
b un
n
1
2
0













55

56. Example: Express in CCF/OCF/DCF
56
CCF
OCF
DCF

57. Converting a Transfer Function to State Space
A set of state variables is called phase variables, where each
subsequent state variable is defined to be the derivative of the
previous state variable.
Consider the differential equation
Choosing the state variables
ubya
dt
dy
a
dt
yd
a
dt
yd
n
n
nn
n
0011
1
1  

 
ubxaxaxa
dt
yd
x
dt
yd
x
x
dt
yd
x
dt
yd
x
x
dt
yd
x
dt
dy
x
x
dt
dy
xyx
nnn
n
nn
n
n 0121101
1
43
3
32
2
3
32
2
22
211











57

58. u
bx
x
x
x
x
aaaaaax
x
x
x
x
n
n
nn
n






















































































0
1
3
2
1
143210
1
3
2
1
0
0
0
0
100000
001000
000100
000010













 






















n
n
x
x
x
x
x
y
1
3
2
1
00001


58

59. Converting a transfer function with constant term in numerator
 Step 1. Find the associated differential equation.
 Step 2. Select the state variables.
Choosing the state variables as successive derivatives.
24269
24
)(
)(
23


ssssR
sC
rcccc
sRsCsss
2424269
)(24)()24269( 23



cx
cx
cx





3
2
1
1
3213
32
21
2492624
xy
rxxxx
xx
xx








59

60. Converting a transfer function with polynomial in numerator
Step1. Decomposing a transfer function.
Step 2. Converting the transfer function with constant term in numerator.
Step 3. Inverse Laplace transform.
01
2
2
3
3
1 1
)(
)(
asasasasR
sX

 )()()()( 101
2
2 sXbsbsbsCsY 
10
1
12
1
2
2)( xb
dt
dx
b
dt
xd
bty 
01
2
2
3
3
1 1
)(
)(
asasasasR
sX


)()()()( 101
2
2 sXbsbsbsCsY 
322110)( xbxbxbty  60

61. Ex. Find the transfer from the state-space representation
u























0
0
10
321
100
010
xx
 x001y





































321
10
01
321
100
010
00
00
00
)(
s
s
s
s
s
s
s AI
Solution:
123
12
31
1323
)det(
)(
)( 23
2
2
2
1

















 
sss
sss
sss
sss
s
sadj
s
AI
AI
AI
123
)23(10
)(
)(
23
2



sss
ss
s
s
U
Y
61

62. 62

63. 63

64. Output Eq. modifies to
64