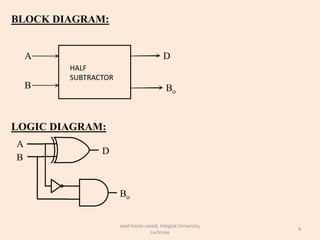
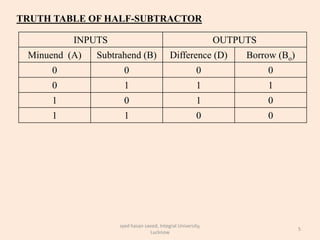
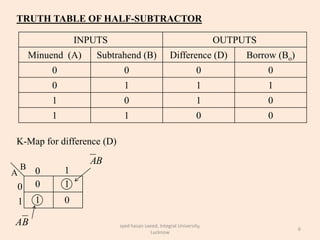
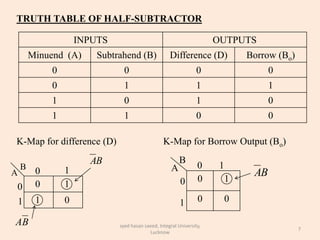
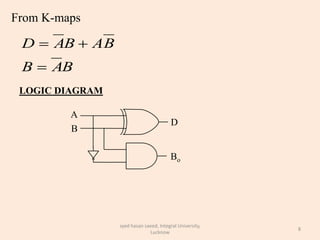
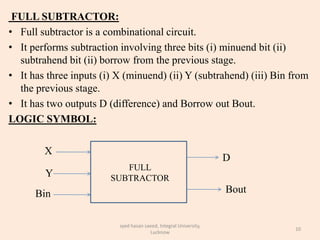
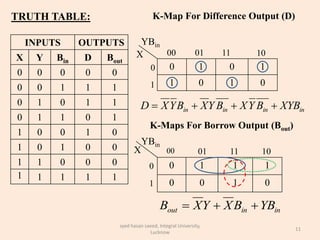
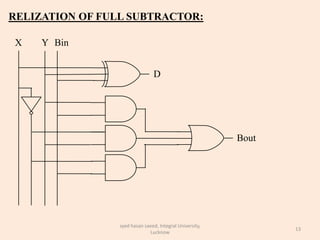
The document discusses binary subtraction and different types of binary subtractors. It describes half subtractors and full subtractors. A half subtractor is a basic circuit that can subtract two binary bits and outputs the difference and borrow. A full subtractor can subtract three bits by also considering the borrow from the previous stage. Truth tables and K-maps are used to derive the logic equations for difference and borrow outputs. Full subtractors are realized using basic gates by complementing one input to convert a full adder circuit into a full subtractor.

1. SYED HASAN SAEED
hasansaeedcontrol@gmail.com
shasansaeed@yolasite.com
1
syed hasan saeed, Integral University,
Lucknow

2. BINARY SUBTRACTOR
RULES FOR BINARY SUBTRACTION
0 - 0 = 0
0 - 1 = 1 with borrow 1
1 - 0 =1
1 – 1=0
NOTE: In the second case (0 – 1) it is necessary to borrow a 1.
2
syed hasan saeed, Integral University,
Lucknow

3. TYPES OF BINARY SUBTRACTOR
• Half Subtractor
• Full Subtractor
Half Subtractor:
• It is a combinational circuit with two inputs and two outputs ( difference
and borrow)
• Two inputs are A (minuend), B (subtrahend) and two outputs are D
(difference) and Bo (borrow out).
• It is used to perform subtraction of two bits.
3
syed hasan saeed, Integral University,
Lucknow

4. BLOCK DIAGRAM:
LOGIC DIAGRAM:
HALF
SUBTRACTOR
D
Bo
A
B
D
Bo
A
B
4
syed hasan saeed, Integral University,
Lucknow

5. INPUTS OUTPUTS
Minuend (A) Subtrahend (B) Difference (D) Borrow (Bo)
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
TRUTH TABLE OF HALF-SUBTRACTOR
5
syed hasan saeed, Integral University,
Lucknow

6. INPUTS OUTPUTS
Minuend (A) Subtrahend (B) Difference (D) Borrow (Bo)
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
TRUTH TABLE OF HALF-SUBTRACTOR
K-Map for difference (D)
0 1
1 0
A
B
BA
BA
0 1
0
1
6
syed hasan saeed, Integral University,
Lucknow

7. INPUTS OUTPUTS
Minuend (A) Subtrahend (B) Difference (D) Borrow (Bo)
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
TRUTH TABLE OF HALF-SUBTRACTOR
K-Map for difference (D) K-Map for Borrow Output (Bo)
0 1
1 0
A
B
BA
BA
0 1
0
1
0 1
0 0
A
B
0
0
1
1
BA
7
syed hasan saeed, Integral University,
Lucknow

8. From K-maps
syed hasan saeed, Integral University,
Lucknow
8
BAB
BABAD


LOGIC DIAGRAM
A
B
D
Bo

9. DISADVANTAGE OF HALF SUBTRACTOR:
Half subtractor can only perform the subtraction of two binary bits. But
while performing the subtraction, it does not take into account the borrow of
the lower significant stage.
HALF SUBTRACTOR USING BASIC GATES:
syed hasan saeed, Integral University,
Lucknow
9
BA
BA
BABAD 
BABO 
A B

10. FULL SUBTRACTOR:
• Full subtractor is a combinational circuit.
• It performs subtraction involving three bits (i) minuend bit (ii)
subtrahend bit (ii) borrow from the previous stage.
• It has three inputs (i) X (minuend) (ii) Y (subtrahend) (iii) Bin from
the previous stage.
• It has two outputs D (difference) and Borrow out Bout.
LOGIC SYMBOL:
syed hasan saeed, Integral University,
Lucknow
10
X
Y
Bin
D
Bout
FULL
SUBTRACTOR

11. TRUTH TABLE:
syed hasan saeed, Integral University,
Lucknow
11
INPUTS OUTPUTS
X Y Bin D Bout
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
K-Map For Difference Output (D)
0 1 0 1
1 0 1 0
X
YBin
00 01 11 10
0
1
inininin XYBBYXBYXBYXD 
K-Maps For Borrow Output (Bout)
0 1 1 1
0 0 1 0
X
YBin
00 01 11 10
0
1
ininout YBBXYXB 

12. syed hasan saeed, Integral University,
Lucknow
12
inininin XYBBYXBYXBYXD 
in
inin
inin
BYXD
BYXBYXD
BYXYXBXYYXD



)()(
)()(
•Equation for a borrow output is resembles the carry output of full adder
except that one of the input is complemented.
• Equation for D is same as the sum of output for a full adder.
•It is possible to convert a full adder into a full subtractor by
complementing that input before to its applied to the input of gates which
form the borrow output.

13. RELIZATION OF FULL SUBTRACTOR:
syed hasan saeed, Integral University,
Lucknow
13
X Y Bin
D
Bout

14. THANK YOU
syed hasan saeed, Integral University,
Lucknow
14